The ttest the paired ttest and introduction to

The t-test, the paired t-test, and introduction to non-parametric tests July 8, 2004

1. The t-test: for comparing means (averages)

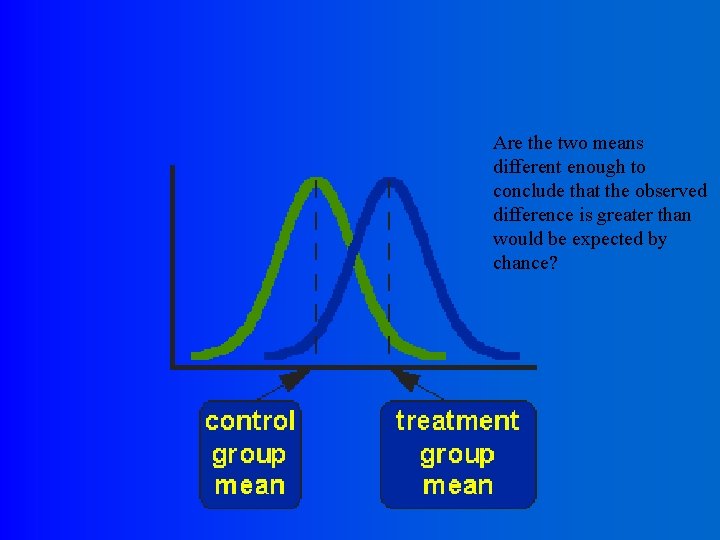
Comparing two means l Is the difference in means that we observe between two groups more than we’d expect to see based on chance alone?

Are the two means different enough to conclude that the observed difference is greater than would be expected by chance?

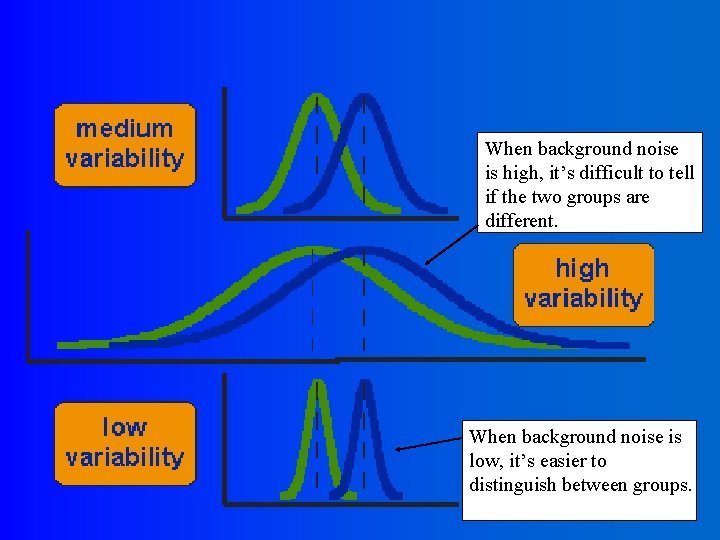
When background noise is high, it’s difficult to tell if the two groups are different. When background noise is low, it’s easier to distinguish between groups.

Comparing two means l What is the sampling distribution of the difference in the means of two samples? l First we need to know: What is the distribution of a difference between two normally distributed random variables?

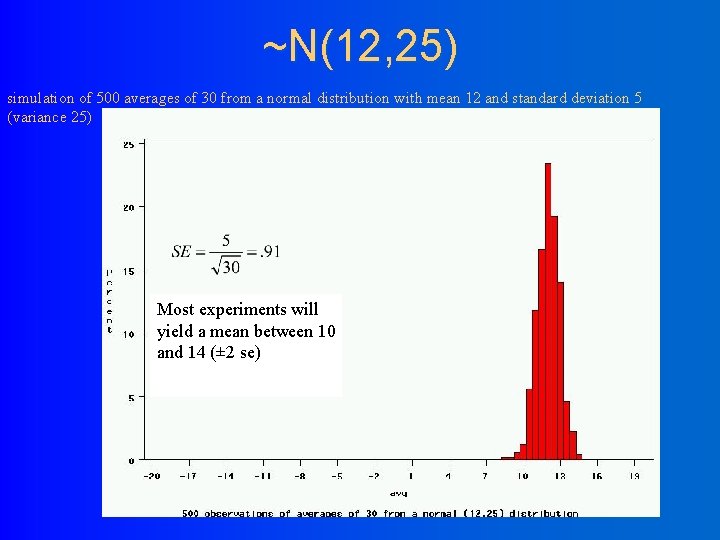
~N(12, 25) simulation of 500 averages of 30 from a normal distribution with mean 12 and standard deviation 5 (variance 25) Most experiments will yield a mean between 10 and 14 (± 2 se)

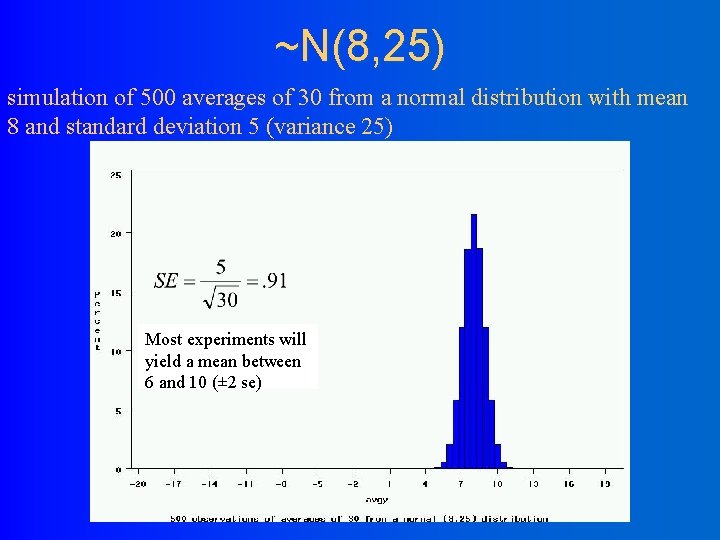
~N(8, 25) simulation of 500 averages of 30 from a normal distribution with mean 8 and standard deviation 5 (variance 25) Most experiments will yield a mean between 6 and 10 (± 2 se)

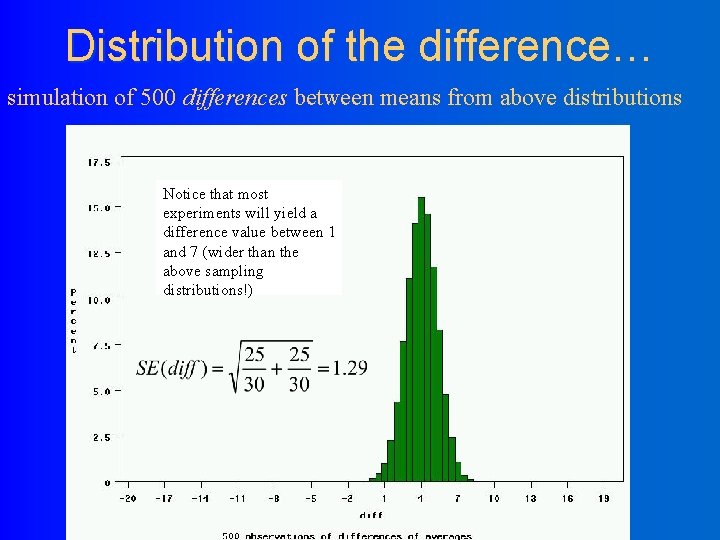
Distribution of the difference… simulation of 500 differences between means from above distributions Notice that most experiments will yield a difference value between 1 and 7 (wider than the above sampling distributions!)

Distribution of differences if X and Y are independent and X ~ N( x, x 2) and Y ~ N( y, y 2) • recall that averages are normally distributed if n is large enough, by the central limit theorem then (X-Y) ~ N( y- x, x 2+ y 2) and (X+Y) ~ N( y+ x, x 2+ y 2) l Therefore, if X and Y are the averages of n and m subjects, respectively:

Example l A particular IQ test is designed to have a range of 0 to 200 with a standard deviation of 10 when given to U. S. adults. You suspect that female doctors have higher IQ’s than male doctors. To test this hypothesis, you take a random sample of 30 female doctors and 30 male doctors. The women score an average of 152 and the men an average of 149. What is your conclusion?

Recall steps of a hypothesis test: l 1. Define your hypotheses (null, alternative) l 2. Specify your null distribution: l 3. Do an experiment l 4. Calculate the p-value of what you observed l 5. Reject or fail to reject (~accept) the null hypothesis

1. Define your hypotheses (null, alternative) H 0: ♀-doctor IQ = ♂-doctor IQ; (♀ - ♂ = 0) Ha: ♀-doctor IQ ≠ ♂-doctor IQ; (♀- ♂ ≠ 0 ) [two-sided]

2. Specify your null distribution Null hypothesis is that the difference is zero.

3. Do an experiment Observed difference in our experiment = 3. 0 IQ points

4. Calculate the p-value of what you observed 3/2. 58=1. 16 Z = (FROM SAS): data _null_; x=(1 -probnorm(1. 16))*2; put x; run; 0. 2460488061 Two sided test! Both tails are possible, so must double the area from one tail. (two-sided p-value)

5. Reject or fail to reject (~accept) the null hypothesis Not enough evidence to reject at the. 05 significance level. (. 24>. 05)

Complication 1… l The harsh reality is, we hardly ever know the true standard deviation a priori. If we knew that much, we probably wouldn’t need to run an experiment! In most cases, we must use the sample standard deviation as a stand-in for the truth. However, by estimating the population standard deviation we are adding more uncertainty to our experiment. The null distribution is slightly wider than a normal curve…called a “t-distribution. ”

Recall: sample variance and standard deviation The variance of a population: 2 = The variance of a sample: s 2 = The standard deviation of a sample: s=

Example: calculation of sample standard deviation l systolic blood pressures: 104, 114, 120, 148, 130, 132, 143, 152, 133, 124 l Mean = 1300/10 = 130 l Sample standard deviation = l. Estimated standard error of the mean=

Complication 1… l The null distribution is slightly wider than a normal curve…called a “t-distribution. ”

The “t” probability density function Where: is the degrees of freedom (gamma) is the Gamma function is the constant Pi (3. 14. . . )

The “t” distributions l The t distribution depends on the degrees of freedom. l Degrees of freedom here=number of observations used to calculate the standard deviation (n) minus the number of sample means (1 or 2) used in calculation of the sample standard deviation

The “t” distributions The t distribution is just a slightly flattened version of the normal curve. l The t distribution is actually a family of distributions that comes closer and closer to the normal probability distribution as degrees of freedom increase. l With n>30, the t distribution is approximately normal. l The t-function in SAS is: probt(t-statistic, df) Degrees of freedom

Example l. A one-sample test when the standard deviation is unknown (one-sample t-test)

Example: One sample t-test l A British sleep researcher claims that the British sleep an average of 6. 0 hours a night. If you ask 30 Brits how many hours they sleep per night and your sample average is 6. 9 hours with a sample standard deviation of 3. 0, do you think the researcher was mistaken in his claim? 1. Specify hypothesis: H 0: average hours = 6. 0 Ha: average hourse ≠ 6. 0 [two-sided]

One sample t-test 2. Specify null distribution. The null distribution here actually follows a “t-distribution with 29 (=n-1) “degrees of freedom” (the higher the number of degrees of freedom, the more the t-distribution looks like a normal curve).

One sample t-test 3. Observed data=6. 9 hours with a sample standard of 3. 0

One sample t-test 4. USE SAS TO CALCULATE p-value: data _null_; pval=1 -probt(1. 64, 29); put pval; run; 0. 0559046876 For two-sided test, multiply by 2: p-value=. 11 – This gives just a slightly higher answer than the Z-test (Z=1. 64), which yields a two-sided p-value of. 10. Diminished certainty due to estimating the standard deviation.

One sample t-test 5. . 11>. 05; do not reject null at a significance level of. 05

Example: two-sample t-test l In 1980, some researchers reported that “men have more mathematical ability than women” as evidenced by the 1979 SAT’s, where a sample of 30 random male adolescents had a mean score ± 1 standard deviation of 436± 77 and 30 random female adolescents scored lower: 416± 81 (genders were similar in educational backgrounds, socioeconomic status, and age). Do you agree with the authors’ conclusions?

Two-sample t-test 1. Define your hypotheses (null, alternative) H 0: ♂-♀ math SAT = 0 Ha: ♂-♀ math SAT ≠ 0 [two-sided]

Two-sample t-test 2. Specify your null distribution: F and M have approximately equal standard deviations/variances, so make a “pooled” estimate of variance.

Two-sample t-test 3. Observed difference in our experiment = 20 points

Two-sample t-test 4. Calculate the p-value of what you observed data _null_; pval=(1 -probt(. 98, 58))*2; put pval; run; 0. 3311563454 5. Do not reject null! No evidence that men are better in math ; )

Example 2 l Example: Rosental, R. and Jacobson, L. (1966) Teachers’ expectancies: Determinates of pupils’ I. Q. gains. Psychological Reports, 19, 115 -118.

The Experiment (note: exact numbers have been altered) Grade 3 at Oak School were given an IQ test at the beginning of the academic year (n=90). l Classroom teachers were given a list of names of students in their classes who had supposedly scored in the top 20 percent; these students were identified as “academic bloomers” (n=18). l BUT: the children on the teachers lists had actually been randomly assigned to the list. l At the end of the year, the same I. Q. test was readministered. l

The results Children who had been randomly assigned to the “top-20 percent” list had mean I. Q. increase of 12. 2 points (sd=2. 0) vs. children in the control group only had an increase of 8. 2 points (sd=2. 5) Is this a statistically significant difference? Give a confidence interval for this difference.

1. Hypotheses H 0: mean change (“gifted”) – mean change (control) = 0 Ha: mean change (“gifted”) – mean change (control) ≠ 0

2. Null distribution of difference of two means:

3. Empirical data Observed difference in our experiment = 12. 2 -8. 2 = 4. 0

4. P-value t-curve with 88 df’s has slightly wider cut -off’s for 95% area (t=1. 99) than a normal curve (Z=1. 96) p-value <. 0001

5. Reject null! l Conclusion: I. Q. scores can bias expectancies in the teachers’ minds and cause them to unintentionally treat “bright” students differently from those seen as less bright.

Confidence interval (more information!!) 95% CI for the difference: 4. 0± 1. 99(. 64) = (2. 7 – 5. 3) t-curve with 88 df’s has slightly wider cutoff’s for 95% area (t=1. 99) than a normal curve (Z=1. 96)

2. The paired T-test

The Paired T-test Paired data: either the same person on different occasions or pairs of people who are more similar to each other than to individuals from other pairs (husband-wife pairs, twin pairs, matched cases and controls, etc. ) l For example, evaluates whether an observed change in mean (before vs. after) represents a true improvement (or decrease). l Null hypothesis: difference (after-before)=0 l

Did the control group in the previous experiment improve at all during the year? p-value <. 0001

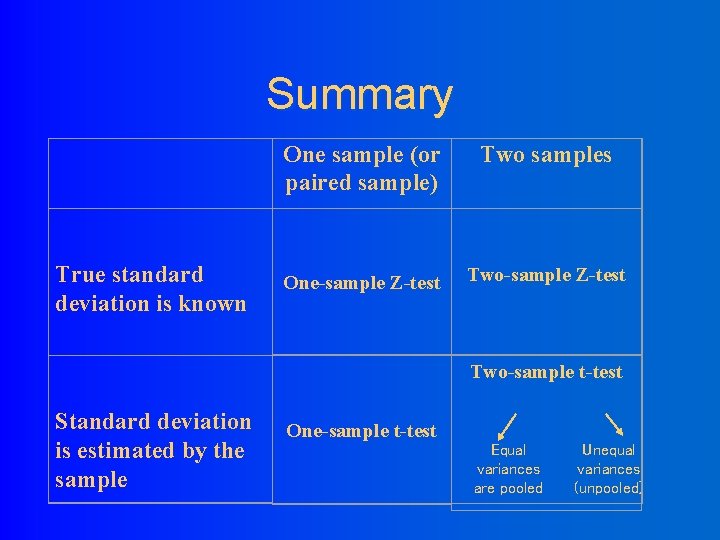
Summary True standard deviation is known One sample (or paired sample) Two samples One-sample Z-test Two-sample t-test Standard deviation is estimated by the sample One-sample t-test Equal variances are pooled Unequal variances (unpooled)

Non-parametric tests l t-tests require your outcome variable to be normally distributed (or close enough). l Non-parametric tests are based on RANKS instead of means and standard deviations (=“population parameters”).

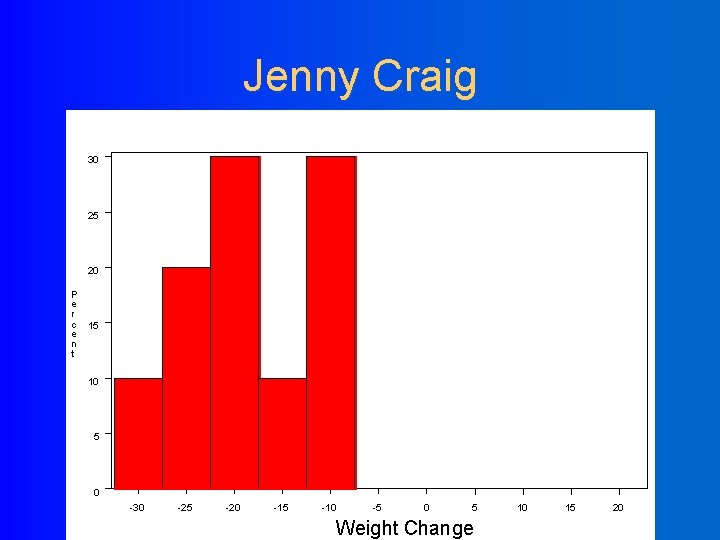
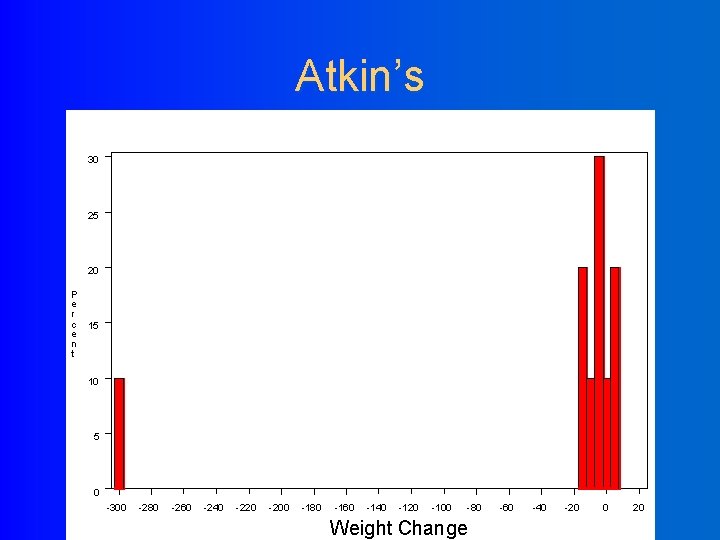
Example: non-parametric tests 10 dieters following Atkin’s diet vs. 10 dieters following Jenny Craig Hypothetical RESULTS: Atkin’s group loses an average of 34. 5 lbs. J. Craig group loses an average of 18. 5 lbs. Conclusion: Atkin’s is better?

Example: non-parametric tests BUT, take a closer look at the individual data… Atkin’s, change in weight (lbs): +4, +3, 0, -3, -4, -5, -11, -14, -15, -300 J. Craig, change in weight (lbs) -8, -10, -12, -16, -18, -20, -21, -24, -26, -30

Jenny Craig 30 25 20 P e r c 15 e n t 10 5 0 -30 -25 -20 -15 -10 -5 0 5 Weight Change 10 15 20

Atkin’s 30 25 20 P e r c 15 e n t 10 5 0 -300 -280 -260 -240 -220 -200 -180 -160 -140 -120 -100 -80 Weight Change -60 -40 -20 0 20

t-test doesn’t work… l Comparing the mean weight loss of the two groups is not appropriate here. l The distributions do not appear to be normally distributed. l Moreover, there is an extreme outlier (this outlier influences the mean a great deal).

Statistical tests to compare ranks: l Wilcoxon Mann-Whitney test is analogue of two-sample t-test.

Wilcoxon Mann-Whitney test l l l l RANK the values, 1 being the least weight loss and 20 being the most weight loss. Atkin’s +4, +3, 0, -3, -4, -5, -11, -14, -15, -300 1, 2, 3, 4, 5, 6, 9, 11, 12, 20 J. Craig -8, -10, -12, -16, -18, -20, -21, -24, -26, -30 7, 8, 10, 13, 14, 15, 16, 17, 18, 19

Wilcoxon Mann-Whitney test l Sum of Atkin’s ranks: l 1+ 2 + 3 + 4 + 5 + 6 + 9 + 11+ 12 + 20=73 l Sum of Jenny Craig’s ranks: 7 + 8 +10+ 13+ 14+ 15+16+ 17+ 18+19=137 l Jenny Craig clearly ranked higher! l P-value *(from computer) =. 018