Testing means part II The paired ttest Outline

Testing means, part II The paired t-test

Outline of lecture • Options in statistics – sometimes there is more than one option • One-sample t-test: review – testing the sample mean • The paired t-test – testing the mean difference

A digression: Options in statistics

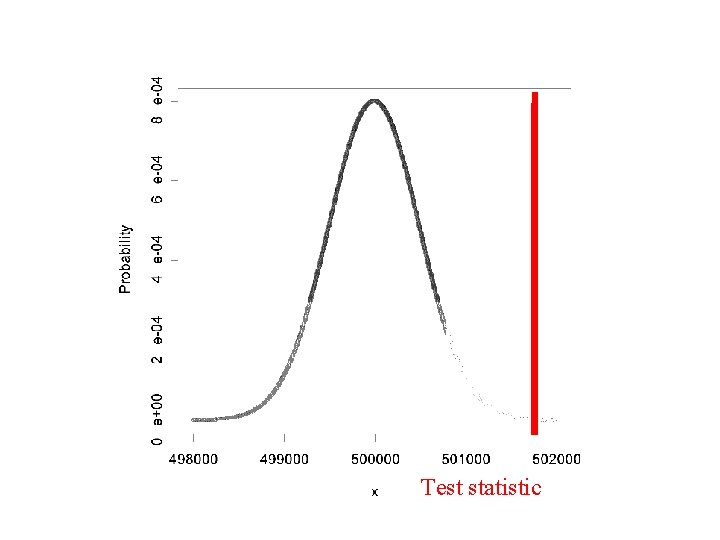
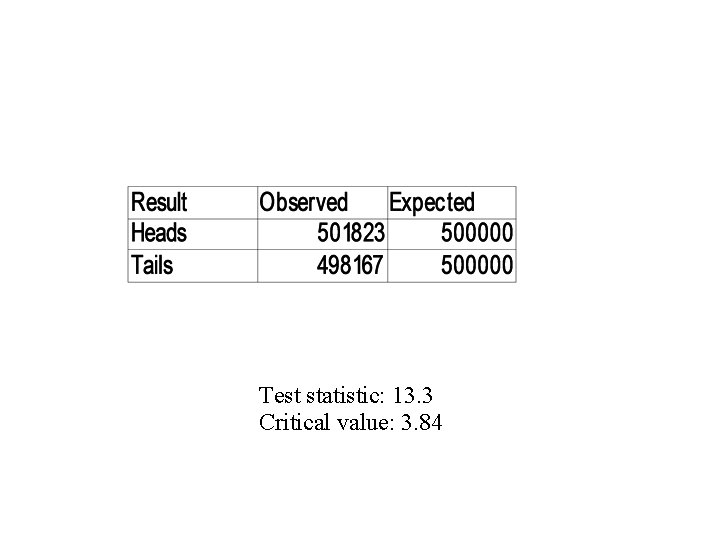
Example • A student wants to check the fairness of the loonie • She flips the coin 1, 000 times, and gets heads 501, 823 times. • Is this a fair coin?

Ho: The coin is fair (pheads = 0. 5). Ha: The coin is not fair (pheads ≠ 0. 5). n = 1, 000 trials x = 501, 823 successes Under the null hypothesis, the number of successes should follow a binomial distribution with n=1, 000 and p=0. 5

Test statistic

Binomial test • P = 2*Pr[X≥ 501, 823] P = 2*(Pr[X = 501, 823] + Pr[X = 501, 824] + Pr[X = 501, 825] + Pr[X = 501, 826] +. . . + Pr[X = 999, 999] + Pr[X = 1, 000]

Central limit theorem The sum or mean of a large number of measurements randomly sampled from any population is approximately normally distributed

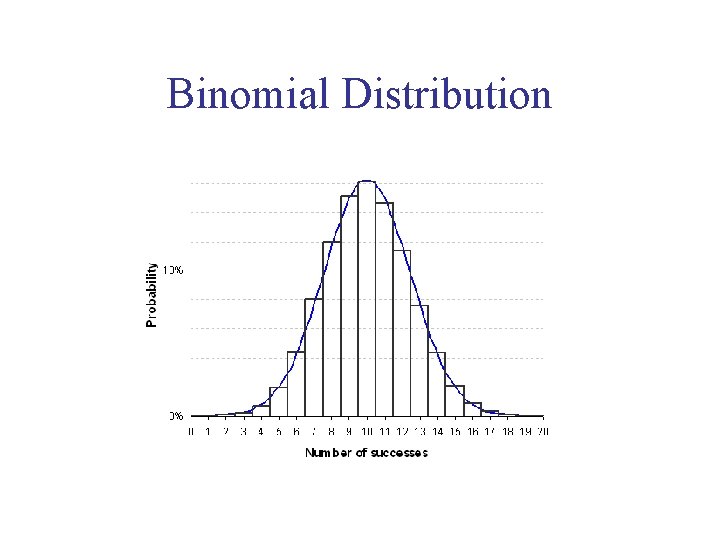
Binomial Distribution

Normal approximation to the binomial distribution

Example • A student wants to check the fairness of the loonie • She flips the coin 1, 000 times, and gets heads 501, 823 times. • Is this a fair coin?

Normal approximation • Under the null hypothesis, data are approximately normally distributed • Mean: np = 1, 000 * 0. 5 = 500, 000 • Standard deviation: • s = 500

Normal distributions • Any normal distribution can be converted to a standard normal distribution, by Z-score

From standard normal table: P = 0. 0001

Conclusion • P = 0. 0001, so we reject the null hypothesis • This is much easier than the binomial test • Can use as long as p is not close to 0 or 1 and n is large

Example • A student wants to check the fairness of the loonie • She flips the coin 1, 000 times, and gets heads 500, 823 times. • Is this a fair coin?

A Third Option! • Chi-squared goodness of fit test • Null expectation: equal number of successes and failures • Compare to chi-squared distribution with 1 d. f.

Test statistic: 13. 3 Critical value: 3. 84

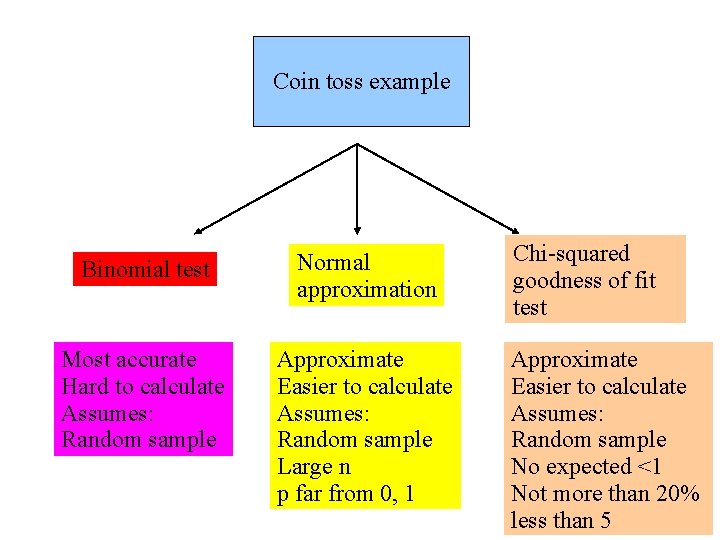
Coin toss example Binomial test Normal approximation Most accurate Hard to calculate Assumes: Random sample Approximate Easier to calculate Assumes: Random sample Large n p far from 0, 1 Chi-squared goodness of fit test Approximate Easier to calculate Assumes: Random sample No expected <1 Not more than 20% less than 5

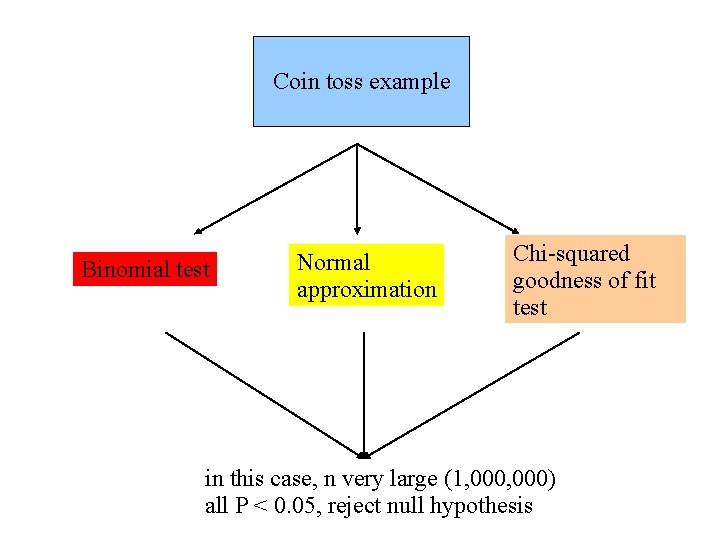
Coin toss example Binomial test Normal approximation Chi-squared goodness of fit test in this case, n very large (1, 000) all P < 0. 05, reject null hypothesis

Normal distributions • Any normal distribution can be converted to a standard normal distribution, by Z-score

t distribution • We carry out a similar transformation on the sample mean under Ho estimated standard error

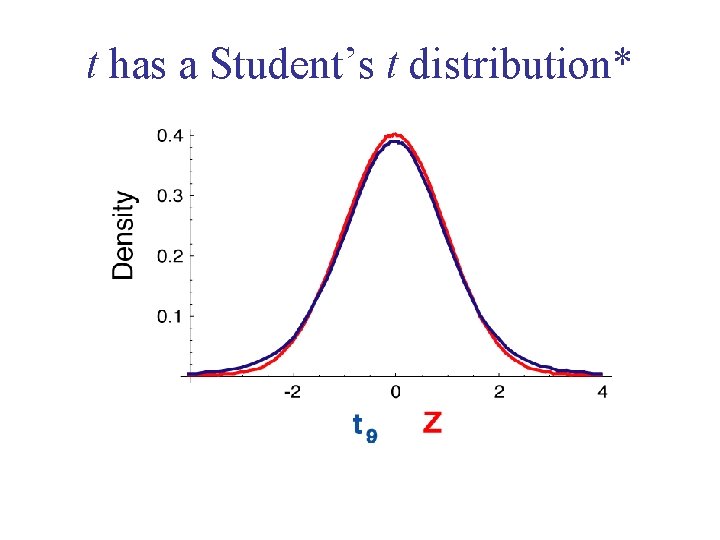
How do we use this? • t has a Student's t distribution • Find confidence limits for the mean • Carry out one-sample t-test

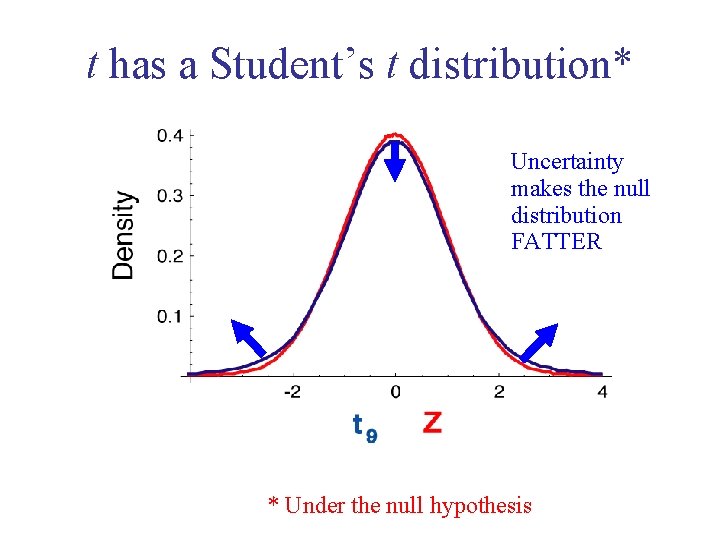
t has a Student’s t distribution*

t has a Student’s t distribution* Uncertainty makes the null distribution FATTER * Under the null hypothesis

Confidence interval for a mean (2) = 2 -tailed significance level df = degrees of freedom, n-1 SEY = standard error of the mean

Confidence interval for a mean 95 % Confidence interval: Use α(2) = 0. 05

Confidence interval for a mean c % Confidence interval: Use α(2) = 1 -c/100

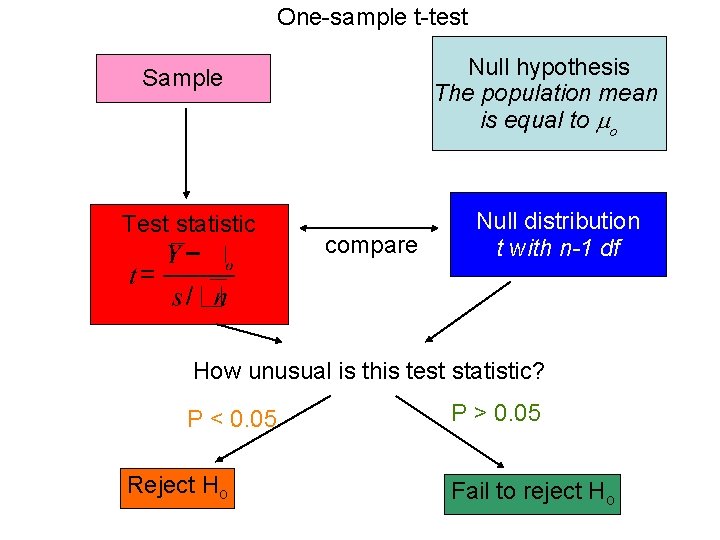
One-sample t-test Null hypothesis The population mean is equal to o Sample Test statistic compare Null distribution t with n-1 df How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

The following are equivalent: • • Test statistic > critical value P < alpha Reject the null hypothesis Statistically significant

Quick reference summary: One-sample t-test • What is it for? Compares the mean of a numerical variable to a hypothesized value, μo • What does it assume? Individuals are randomly sampled from a population that is normally distributed • Test statistic: t • Distribution under Ho: t-distribution with n-1 degrees of freedom • Formulae: Y = sample mean, s = sample standard deviation

Comparing means • Goal: to compare the mean of a numerical variable for different groups. • Tests one categorical vs. one numerical variable Example: gender (M, F) vs. height 32

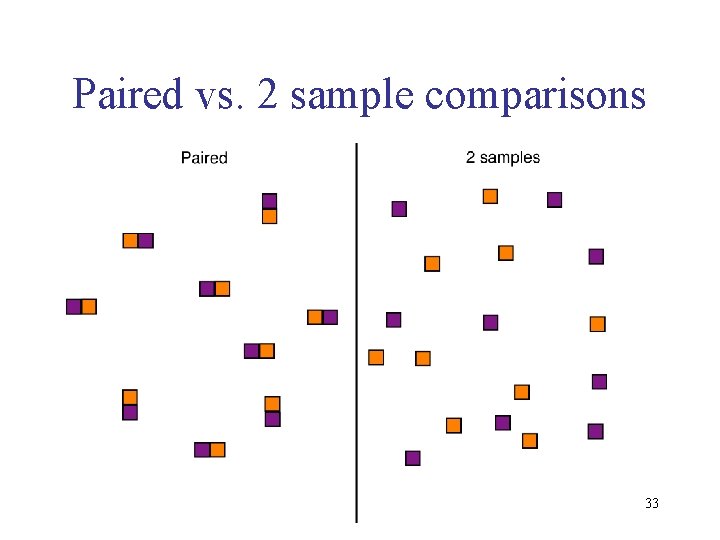
Paired vs. 2 sample comparisons 33

Paired designs • Data from the two groups are paired • There is a one-to-one correspondence between the individuals in the two groups 34

More on pairs • Each member of the pair shares much in common with the other, except for the tested categorical variable • Example: identical twins raised in different environments • Can use the same individual at different points in time • Example: before, after medical treatment 35

Paired design: Examples • Same river, upstream and downstream of a power plant • Tattoos on both arms: how to get them off? Compare lasers to dermabrasion 36

Paired comparisons - setup • We have many pairs • In each pair, there is one member that has one treatment and another who has another treatment • “Treatment” can mean “group” 37

Paired comparisons • To compare two groups, we use the mean of the difference between the two members of each pair 38

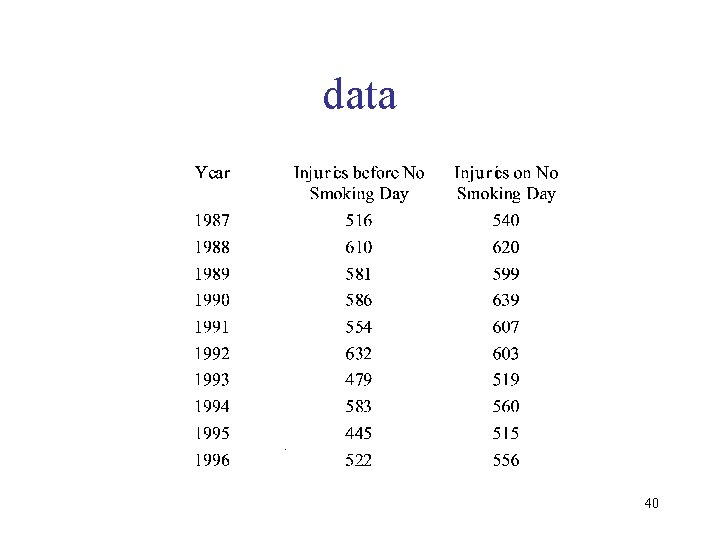
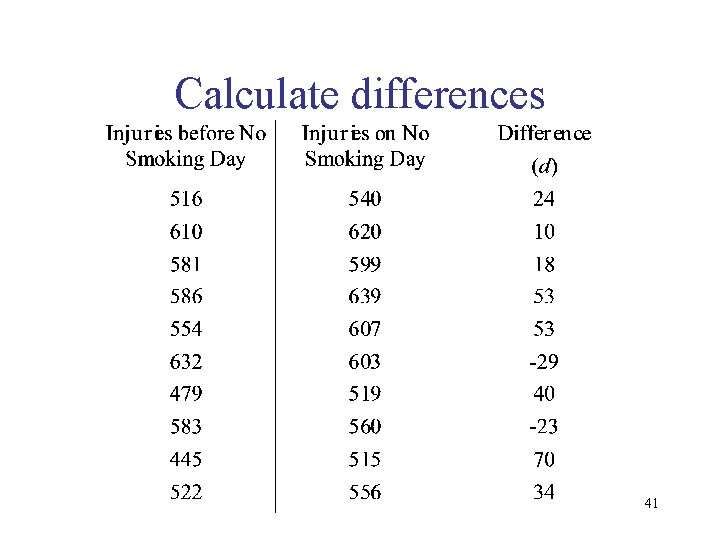
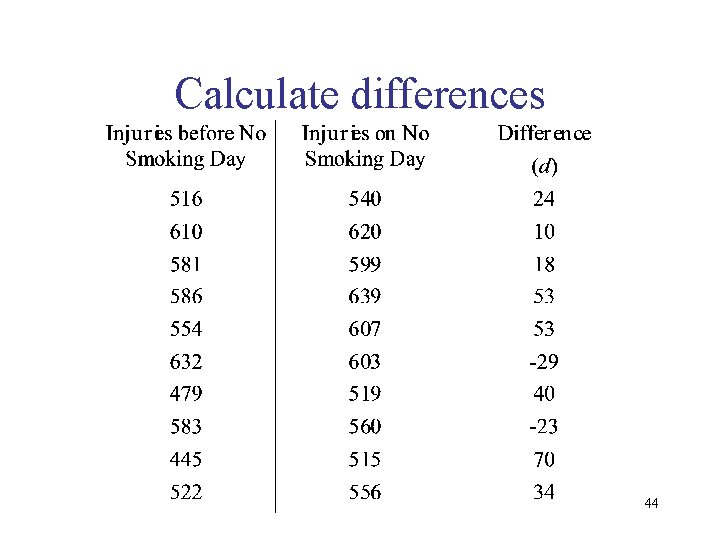
Example: National No Smoking Day • Data compares injuries at work on National No Smoking Day (in Britain) to the same day the week before • Each data point is a year 39

data 40

Calculate differences 41

Paired t test • Compares the mean of the differences to a value given in the null hypothesis • For each pair, calculate the difference. • The paired t-test is a one-sample t-test on the differences. 42

Hypotheses Ho: Work related injuries do not change during No Smoking Days (μ=0) Ha: Work related injuries change during No Smoking Days (μ≠ 0) 43

Calculate differences 44

Calculate t using d’s 45

Caution! • The number of data points in a paired t test is the number of pairs. -- Not the number of individuals • Degrees of freedom = Number of pairs - 1 Here, df = 10 -1 = 9 46

Critical value of t Test statistic: t = 2. 45 So we can reject the null hypothesis: Stopping smoking increases job-related accidents in the short term. 47

Assumptions of paired t test • Pairs are chosen at random • The differences have a normal distribution It does not assume that the individual values are normally distributed, only the differences. 48

Quick reference summary: Paired t-test • What is it for? To test whether the mean difference in a population equals a null hypothesized value, μdo • What does it assume? Pairs are randomly sampled from a population. The differences are normally distributed • Test statistic: t • Distribution under Ho: t-distribution with n-1 degrees of freedom, where n is the number of pairs • Formula: