Testing means part III The twosample ttest Onesample

Testing means, part III The two-sample t-test

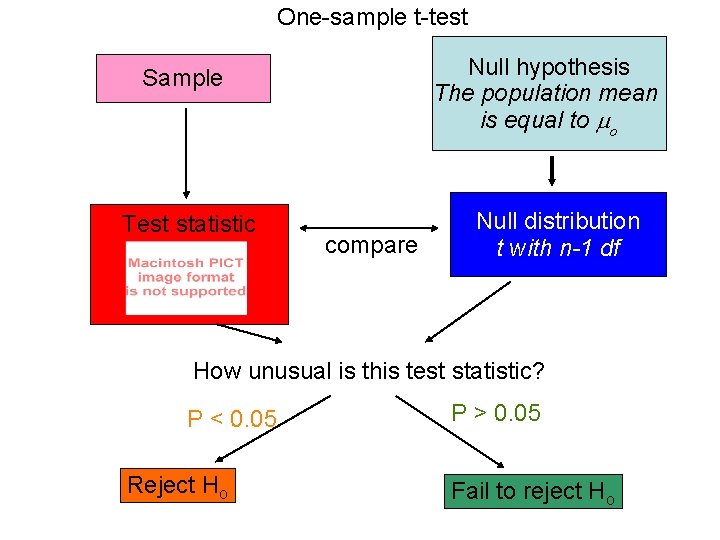
One-sample t-test Null hypothesis The population mean is equal to o Sample Test statistic compare Null distribution t with n-1 df How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

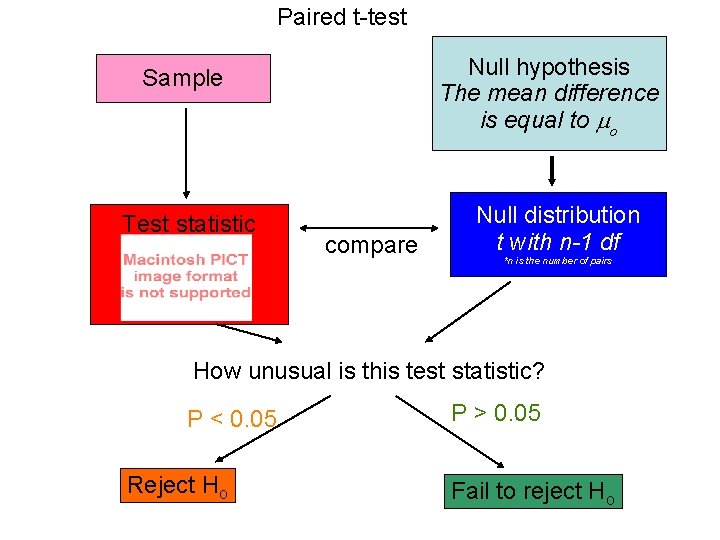
Paired t-test Null hypothesis The mean difference is equal to o Sample Test statistic compare Null distribution t with n-1 df *n is the number of pairs How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Comparing means • Tests with one categorical and one numerical variable • Goal: to compare the mean of a numerical variable for different groups. 4

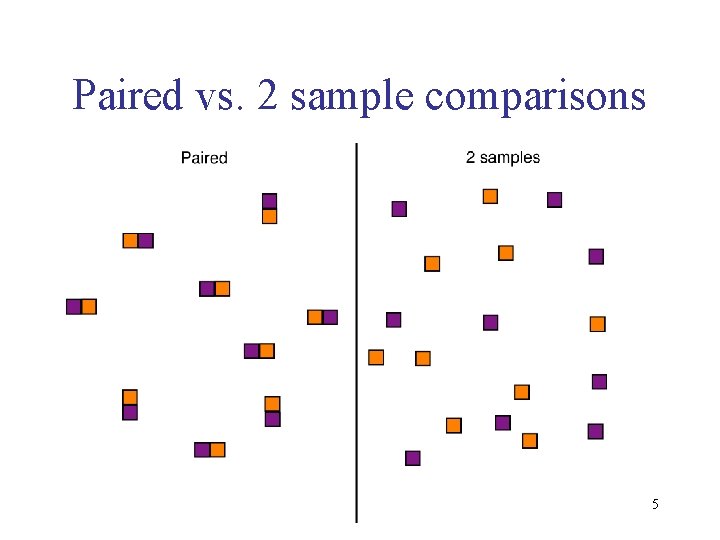
Paired vs. 2 sample comparisons 5

2 Sample Design • Each of the two samples is a random sample from its population 6

2 Sample Design • Each of the two samples is a random sample from its population • The data cannot be paired 7

2 Sample Design - assumptions • Each of the two samples is a random sample • In each population, the numerical variable being studied is normally distributed • The standard deviation of the numerical variable in the first population is equal to the standard deviation in the second population 8

Estimation: Difference between two means Normal distribution Standard deviation s 1=s 2=s Since both Y 1 and Y 2 are normally distributed, their difference will also follow a normal distribution 9

Estimation: Difference between two means Confidence interval: 10

Standard error of difference in means = pooled sample variance = size of sample 1 = size of sample 2 11

Standard error of difference in means Pooled variance: 12

Standard error of difference in means Pooled variance: df 1 = degrees of freedom for sample 1 = n 1 -1 df 2 = degrees of freedom for sample 2 = n 2 -1 s 12 = sample variance of sample 1 s 22 = sample variance of sample 2 13

Estimation: Difference between two means Confidence interval: 14

Estimation: Difference between two means Confidence interval: df = df 1 + df 2 = n 1+n 2 -2 15

Costs of resistance to disease 2 genotypes of lettuce: Susceptible and Resistant Do these differ in fitness in the absence of disease? 16

Data, summarized Both distributions are approximately normal. 17

Calculating the standard error df 1 =15 -1=14; df 2 = 16 -1=15 18

Calculating the standard error df 1 =15 -1=14; df 2 = 16 -1=15 19

Calculating the standard error df 1 =15 -1=14; df 2 = 16 -1=15 20

Finding t df = df 1 + df 2= n 1+n 2 -2 = 15+16 -2 =29 21

Finding t df = df 1 + df 2= n 1+n 2 -2 = 15+16 -2 =29 22

The 95% confidence interval of the difference in the means 23

Testing hypotheses about the difference in two means 2 -sample t-test 24

2 -sample t-test Test statistic: 25

Hypotheses 26

Null distribution df = df 1 + df 2 = n 1+n 2 -2 27

Calculating t 28

Drawing conclusions. . . Critical value: t 0. 05(2), 29=2. 05 t <2. 05, so we cannot reject the null hypothesis. These data are not sufficient to say that there is a cost of resistance. 29

Assumptions of two-sample t tests • Both samples are random samples. • Both populations have normal distributions • The variance of both populations is equal. 30

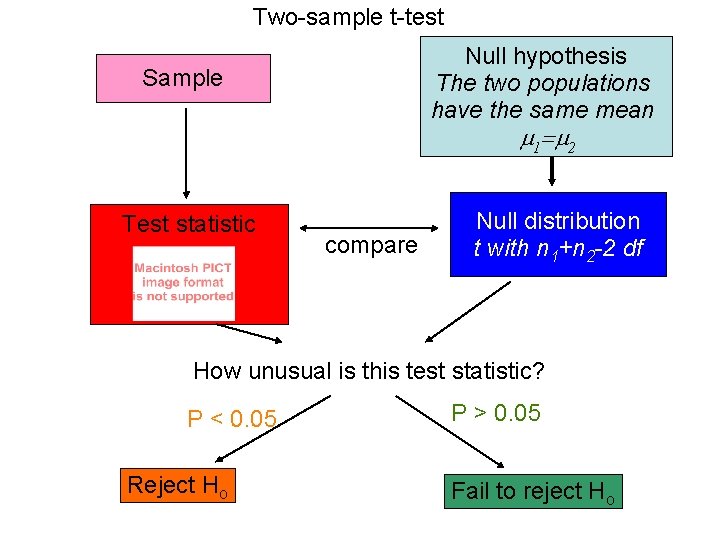
Two-sample t-test Null hypothesis The two populations have the same mean Sample 1 2 Test statistic compare Null distribution t with n 1+n 2 -2 df How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Quick reference summary: Two-sample t-test • What is it for? Tests whether two groups have the same mean • What does it assume? Both samples are random samples. The numerical variable is normally distributed within both populations. The variance of the distribution is the same in the two populations • Test statistic: t • Distribution under Ho: t-distribution with n 1+n 2 -2 degrees of freedom. • Formulae:

Comparing means when variances are not equal Welch’s t test 33

Burrowing owls and dung traps 34

Dung beetles 35

Experimental design • 20 randomly chosen burrowing owl nests • Randomly divided into two groups of 10 nests • One group was given extra dung; the other not • Measured the number of dung beetles on the owls’ diets 36

Number of beetles caught • Dung added: • No dung added: 37

Hypotheses H 0: Owls catch the same number of dung beetles with or without extra dung ( 1 = 2) HA: Owls do not catch the same number of dung beetles with or without extra dung ( 1 2) 38

Welch’s t Round down df to nearest integer 39

Owls and dung beetles 40

Degrees of freedom Which we round down to df= 10 41

Reaching a conclusion t 0. 05(2), 10= 2. 23 t=4. 01 > 2. 23 So we can reject the null hypothesis with P<0. 05. Extra dung near burrowing owl nests increases the number of dung beetles eaten. 42

Quick reference summary: Welch’s approximate t-test • What is it for? Testing the difference between means of two groups when the standard deviations are unequal • What does it assume? Both samples are random samples. The numerical variable is normally distributed within both populations • Test statistic: t • Distribution under Ho: t-distribution with adjusted degrees of freedom • Formulae:

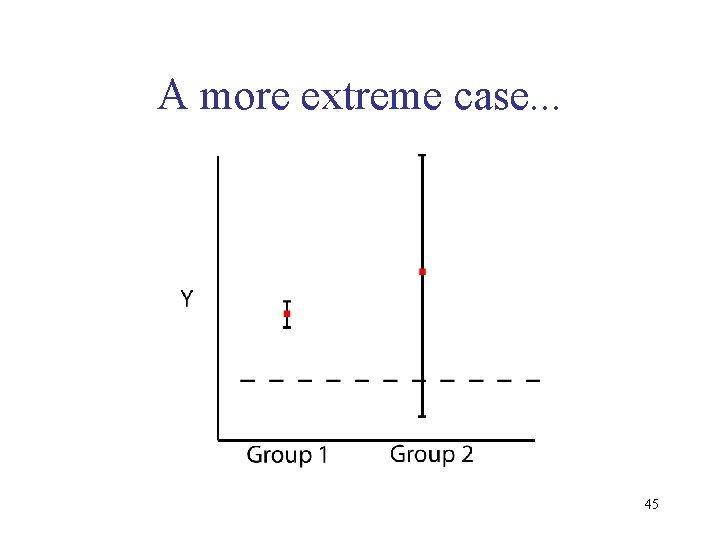
The wrong way to make a comparison of two groups “Group 1 is significantly different from a constant, but Group 2 is not. Therefore Group 1 and Group 2 are different from each other. ” 44

A more extreme case. . . 45