Temple University CIS Dept CIS 616 Principles of


























































![R-trees n [Guttman 84] Main idea: allow parents to overlap! n n n => R-trees n [Guttman 84] Main idea: allow parents to overlap! n n n =>](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-96.jpg)















![R-trees - nn search n A 2: [Roussopoulos+, sigmod 95]: n n priority queue, R-trees - nn search n A 2: [Roussopoulos+, sigmod 95]: n n priority queue,](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-133.jpg)


![R-trees - nn search n variations: [Hjaltason & Samet] incremental nn: n n build R-trees - nn search n variations: [Hjaltason & Samet] incremental nn: n n build](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-138.jpg)


![R-trees - spatial joins Improvements - variations: - [Seeger+, sigmod 92]: do some pre-filtering; R-trees - spatial joins Improvements - variations: - [Seeger+, sigmod 92]: do some pre-filtering;](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-143.jpg)



![R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i. R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i.](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-147.jpg)
![R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i. R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i.](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-148.jpg)














- Slides: 164

Temple University – CIS Dept. CIS 616– Principles of Data Management V. Megalooikonomou Spatial Access Methods (SAMs) (based on notes by Silberchatz, Korth, and Sudarshan and notes by C. Faloutsos at CMU)

General Overview n Multimedia Indexing n Spatial Access Methods (SAMs) n n n k-d trees Point Quadtrees MX-Quadtree z-ordering R-trees

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer spatial queries (like? ? )

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ queries)

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ queries)

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ queries)

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ queries)

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ within ε)

SAMs - motivation n Q: applications?

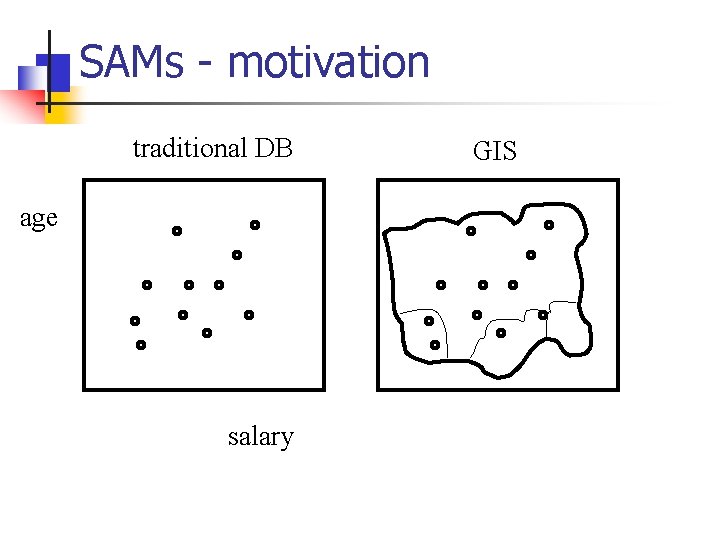
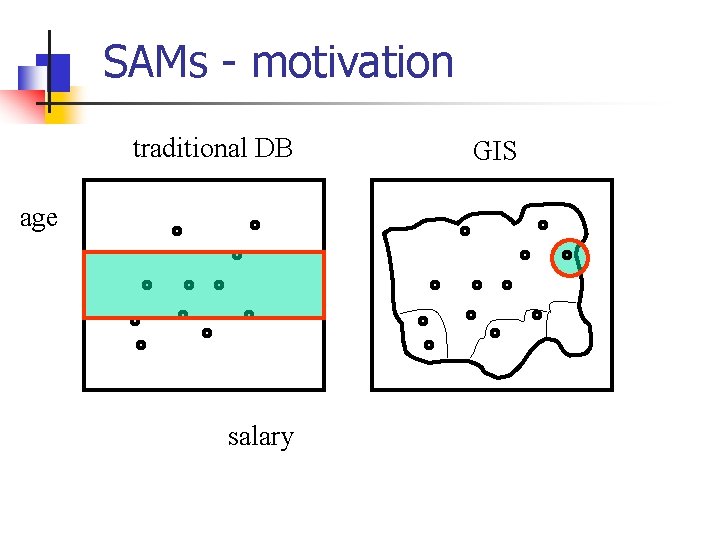
SAMs - motivation traditional DB age salary GIS

SAMs - motivation traditional DB age salary GIS

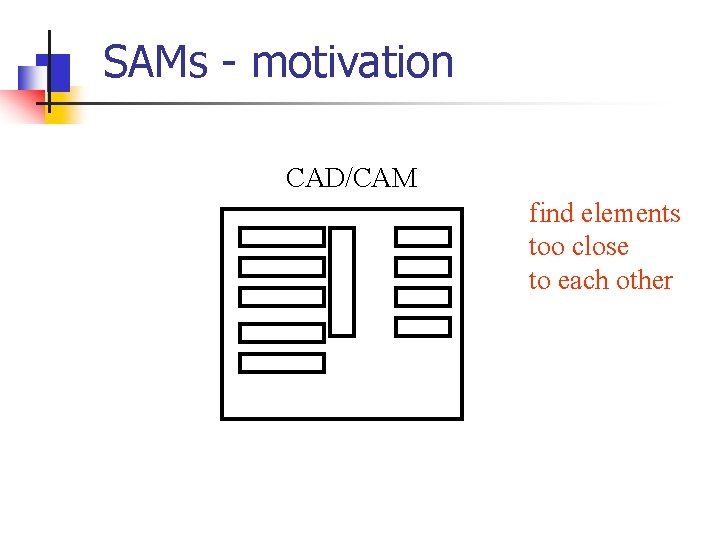
SAMs - motivation CAD/CAM find elements too close to each other

SAMs - motivation CAD/CAM

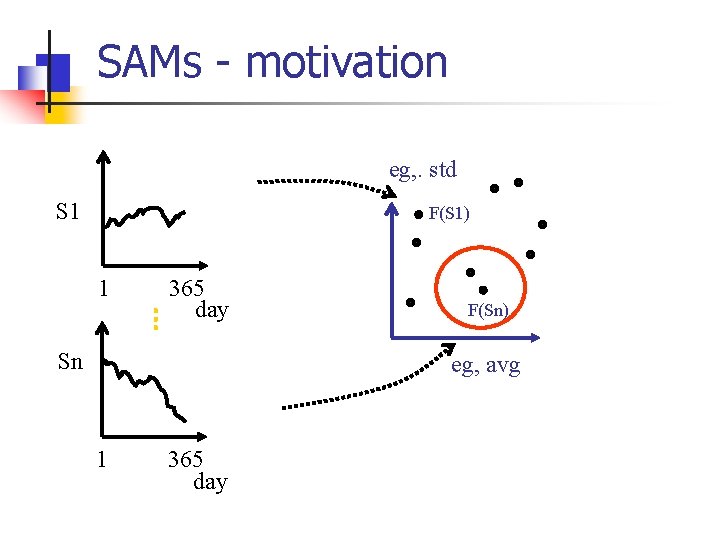
SAMs - motivation eg, . std S 1 F(S 1) 1 365 day Sn F(Sn) eg, avg 1 365 day

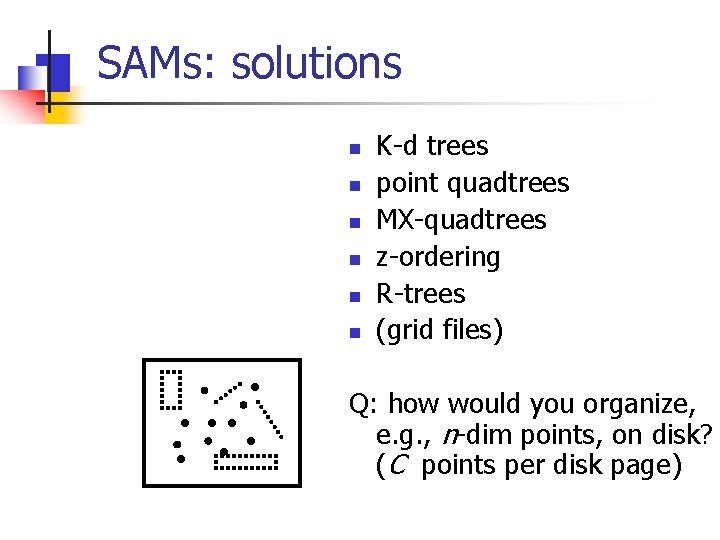
SAMs: solutions n n n K-d trees point quadtrees MX-quadtrees z-ordering R-trees (grid files) Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page)

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

k-d trees n n n Used to store k dimensional point data It is not used to store region data A 2 -d tree (i. e. , for k=2) stores 2 -dimensional point data while a 3 -d tree stores 3 dimensional point data, etc.

2 -d trees – node structure n n n Binary trees Info: information field Xval, Yval: coordinates of a point associated with the node Llink, Rlink: pointers to children Properties (N: node): n If level N even -> n n n for all nodes M in the subtree rooted at N. Llink: M. Xval < N. Xval for all nodes P in the subtree rooted at N. Rlink: P. Xval >= N. Xval If level N odd -> n Similarly use Yvals

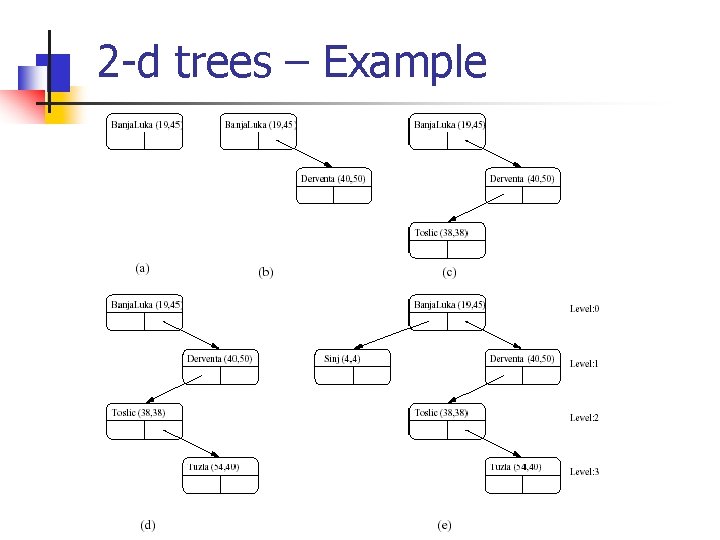
2 -d trees – Example

2 -d trees: Insertion/Search n To insert a node N into the tree pointed by T n n n If N and T agree on Xval, Yval then overwrite T Else, branch left if N. Xval < T. xval, right otherwise (even levels) Similarly for odd levels (branching on Yvals)

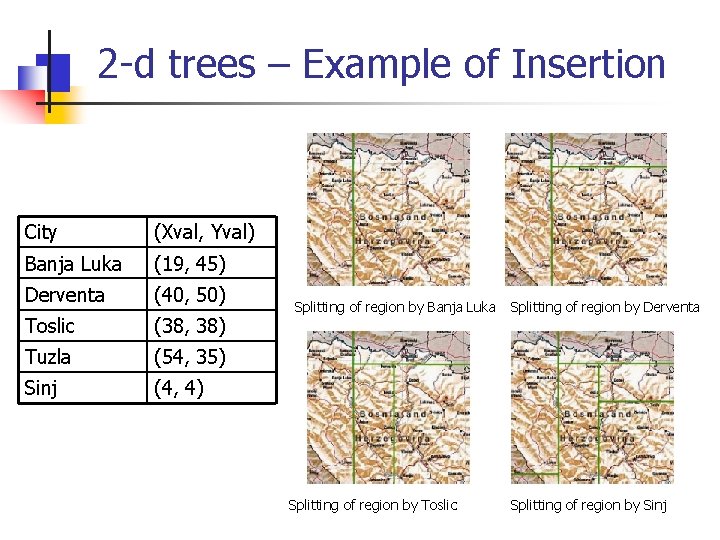
2 -d trees – Example of Insertion City (Xval, Yval) Banja Luka (19, 45) Derventa (40, 50) Toslic (38, 38) Tuzla (54, 35) Sinj (4, 4) Splitting of region by Banja Luka Splitting of region by Toslic Splitting of region by Derventa Splitting of region by Sinj

2 -d trees: Deletion n Deletion of point (x, y) from T n n If N is a leaf node easy Otherwise either Tl (left subtree) or Tr (right subtree) is non-empty n n Find a “candidate replacement” node R in Tl or Tr Replace all of N’s non-link fields by those of R Recursively delete R from Ti Recursion guaranteed to terminate - Why?

2 -d trees: Deletion n Finding candidate replacement nodes for deletion n Replacement node R must bear same spatial relation to all nodes in Tl and Tr as node N

2 -d trees: Range Queries n n Q: Given a point (xc, yc) and a distance r find all points in the 2 -d tree that lie within the circle A: Each node N in a 2 -d tree implicitly represents a region RN – If the circle (specified by the query) has no intersection with RN then there is no point in searching the subtree rooted at node N

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees z-ordering R-trees

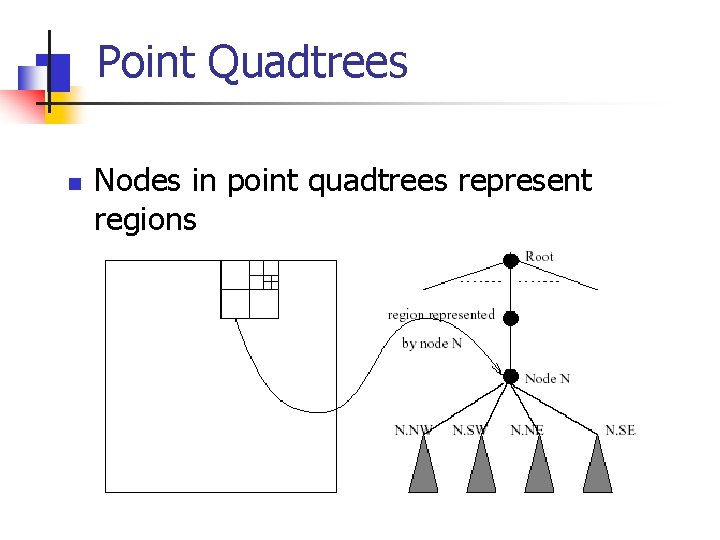
Point Quadtrees n n n Represent point data Always split regions into 4 parts 2 -d tree: a node N splits a region into two by drawing one line through the point (N. xval, N. yval) Point quadtree: a node N splits a region by drawing a horizontal and a vertical line through the point (N. xval, N. yval) Four parts: NW, SW, NE, and SE quadrants Q: Quadtree nodes have 4 children?

Point Quadtrees n Nodes in point quadtrees represent regions

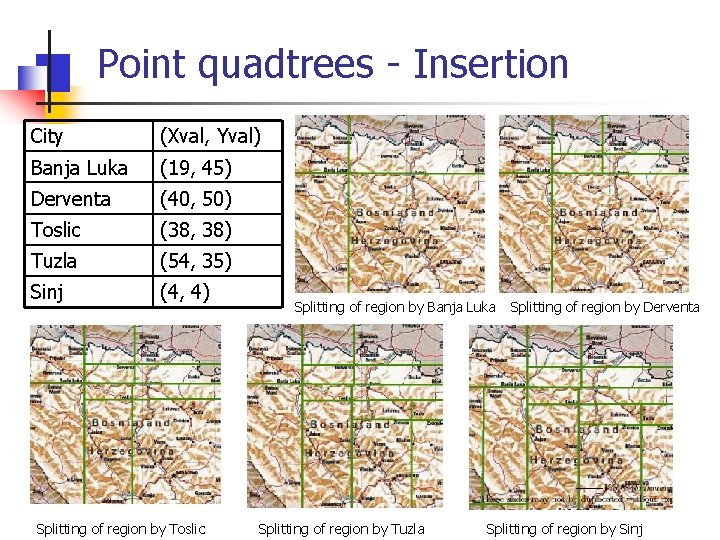
Point quadtrees - Insertion City (Xval, Yval) Banja Luka (19, 45) Derventa (40, 50) Toslic (38, 38) Tuzla (54, 35) Sinj (4, 4) Splitting of region by Toslic Splitting of region by Banja Luka Splitting of region by Tuzla Splitting of region by Derventa Splitting of region by Sinj

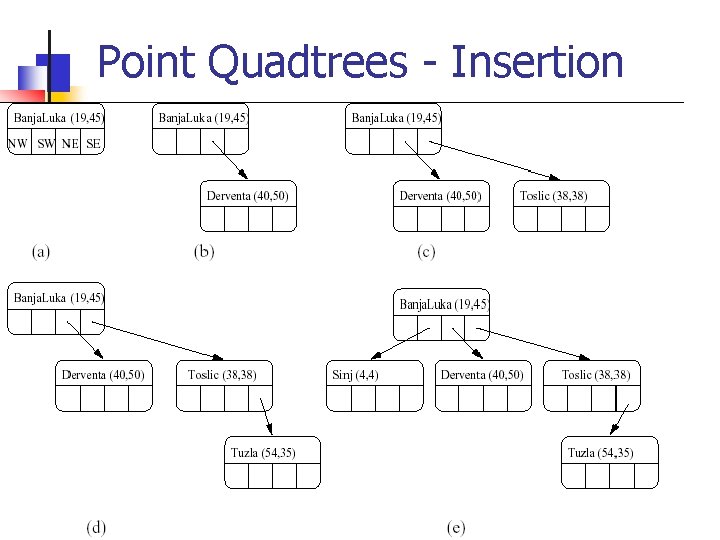
Point Quadtrees - Insertion

Point quadtrees: Deletion n Deletion of point (x, y) from T n n If N is a leaf node easy Otherwise a subtree (N. NW, N. SW, N. NE. N. SE) is nonempty n Find a “candidate replacement” node R in one of the subtrees such that: n n n n Every other node R 1 in N. NW is to the NW of R Every other node R 2 in N. SW is to the SW of R etc… Replace all of N’s non-link fields by those of R Recursively delete R from Ti In general, it may not always be possible to find such as replacement node Q: What happens in the worst case?

Point quadtrees: Deletion n Deletion of point (x, y) from T n n If N is a leaf node easy Otherwise a subtree (N. NW, N. SW, N. NE. N. SE) is nonempty n Find a “candidate replacement” node R in one of the subtrees such that: n n n n Every other node R 1 in N. NW is to the NW of R Every other node R 2 in N. SW is to the SW of R etc… Replace all of N’s non-link fields by those of R Recursively delete R from Ti In general, it may not always be possible to find such as replacement node Q: What happens in the worst case? May require all nodes to be reinserted

Point quadtrees: Range Searches n n Each node in a point quadtree represents a region Do not search regions that do not intersect the circle defined by the query

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

MX-Quadtrees n Drawbacks of 2 -d trees, point quadtrees: n n n shape of tree depends upon the order in which objects are inserted into the tree splits may be uneven depending upon where the point (N. xval, N. yval) is located inside the region (represented by N) MX-quadtrees: shape (and height) of tree independent of number of nodes and order of insertion

MX-Quadtrees n n Assumption: the map is represented as a grid of size (2 k x 2 k) for some k When a region gets “split” it splits down the middle

MX-Quadtrees - Insertion After insertion of A, B, C, and D respectively

MX-Quadtrees - Insertion After insertion of A, B, C, and D respectively

MX-Quadtrees - Deletion n Fairly easy – why? All point are represented at the leaf level Total time for deletion: O(k)

MX-Quadtrees –Range Queries n n Same as in point quadtrees One difference: n Checking to see if a point is in the circle defined by the range query needs to be performed at the leaf level (points are stored at the leaf level)

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

z-ordering Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page) Hint: reduce the problem to 1 -d points(!!) Q 1: why? A: Q 2: how?

z-ordering Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page) Hint: reduce the problem to 1 -d points (!!) Q 1: why? A: B-trees! Q 2: how?

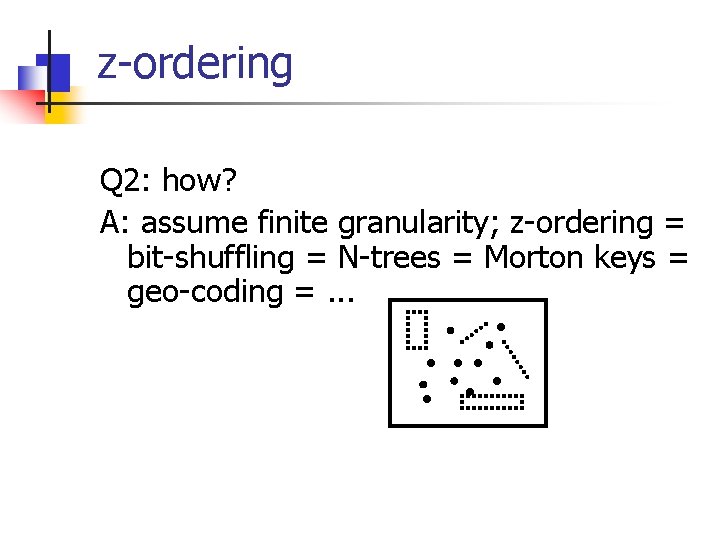
z-ordering Q 2: how? A: assume finite granularity; z-ordering = bit-shuffling = N-trees = Morton keys = geo-coding =. . .

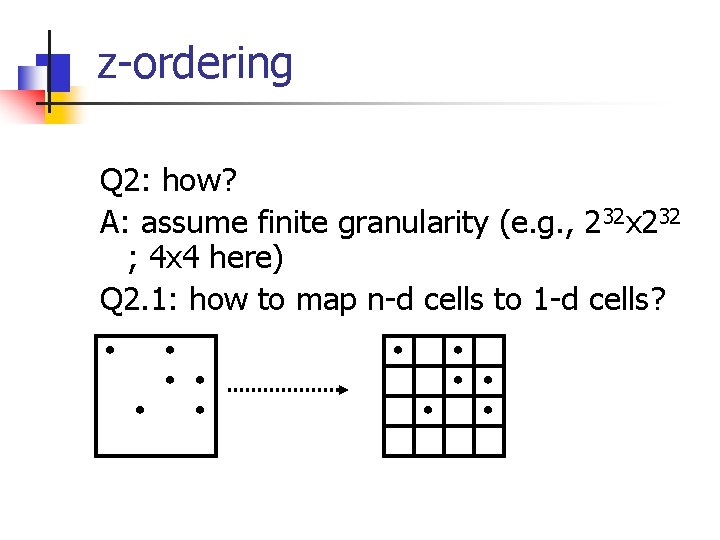
z-ordering Q 2: how? A: assume finite granularity (e. g. , 232 x 232 ; 4 x 4 here) Q 2. 1: how to map n-d cells to 1 -d cells?

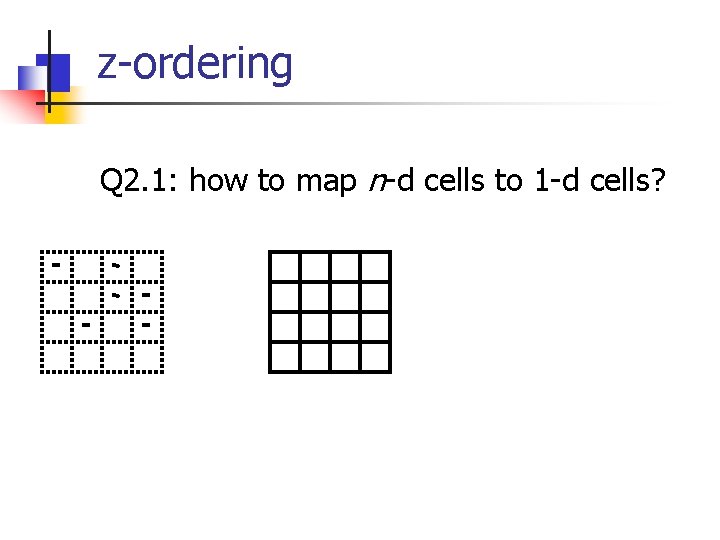
z-ordering Q 2. 1: how to map n-d cells to 1 -d cells?

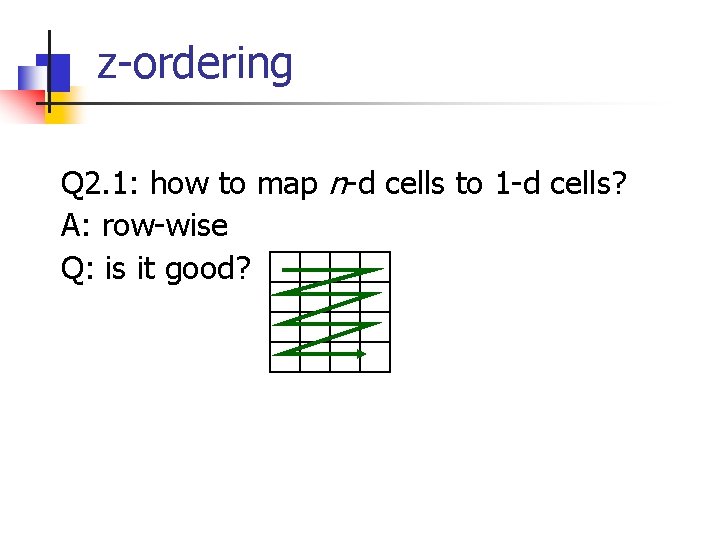
z-ordering Q 2. 1: how to map n-d cells to 1 -d cells? A: row-wise Q: is it good?

z-ordering Q: is it good? A: great for ‘x’ axis; bad for ‘y’ axis

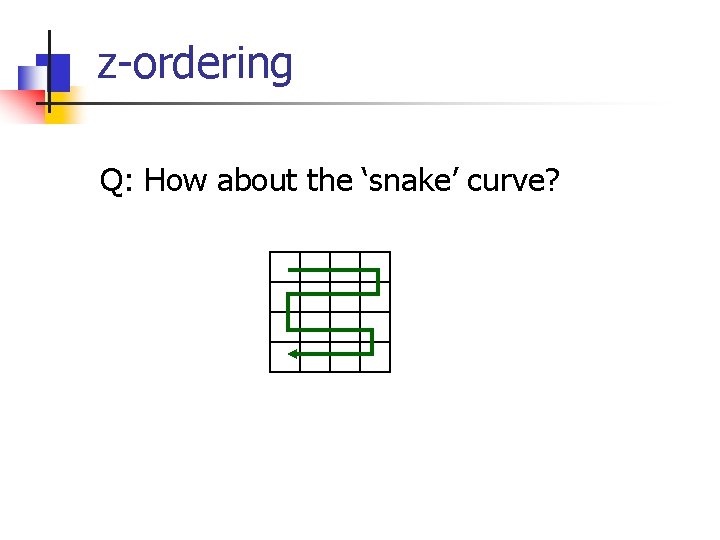
z-ordering Q: How about the ‘snake’ curve?

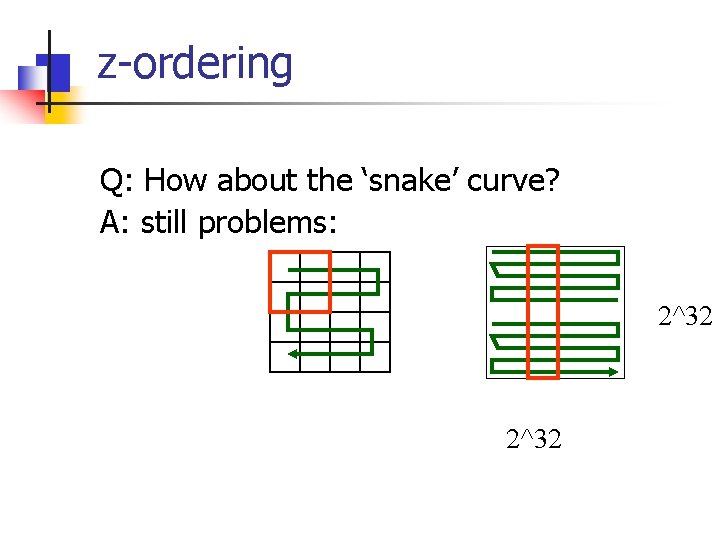
z-ordering Q: How about the ‘snake’ curve? A: still problems: 2^32

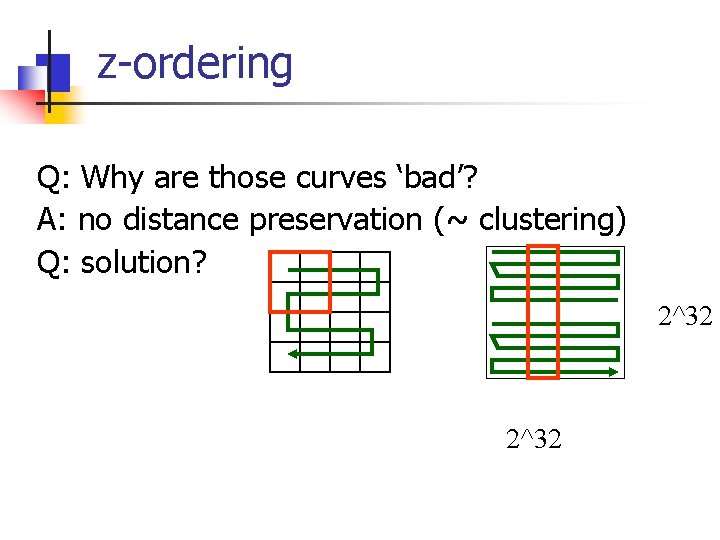
z-ordering Q: Why are those curves ‘bad’? A: no distance preservation (~ clustering) Q: solution? 2^32

z-ordering Q: solution? (w/ good clustering, and easy to compute, for 2 -d and n-d? )

z-ordering Q: solution? (w/ good clustering, and easy to compute, for 2 -d and n-d? ) A: z-ordering/bit-shuffling/linearquadtrees ‘looks’ better: • few long jumps; • scoops out the whole quadrant before leaving it • a. k. a. space filling curves

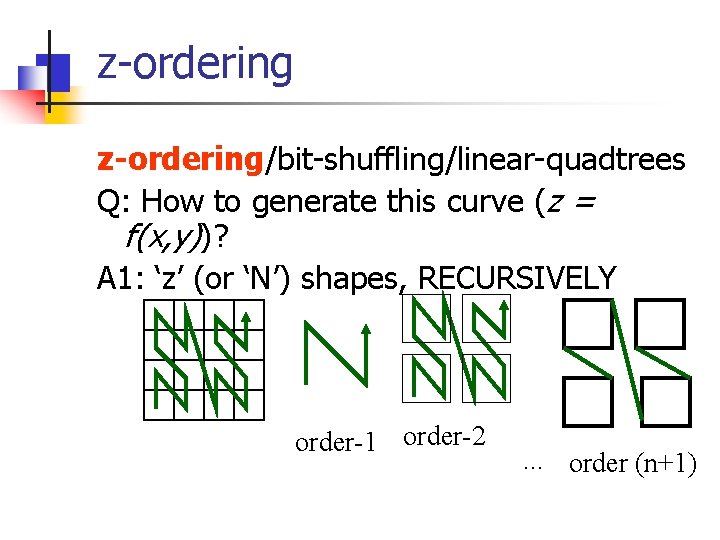
z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers!

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y))? A 1: ‘z’ (or ‘N’) shapes, RECURSIVELY order-1 order-2 . . . order (n+1)

z-ordering Notice: n self similar (we’ll see about fractals, soon) n method is hard to use: z =? f(x, y) order-1 order-2 . . . order (n+1)

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers! Method #2?

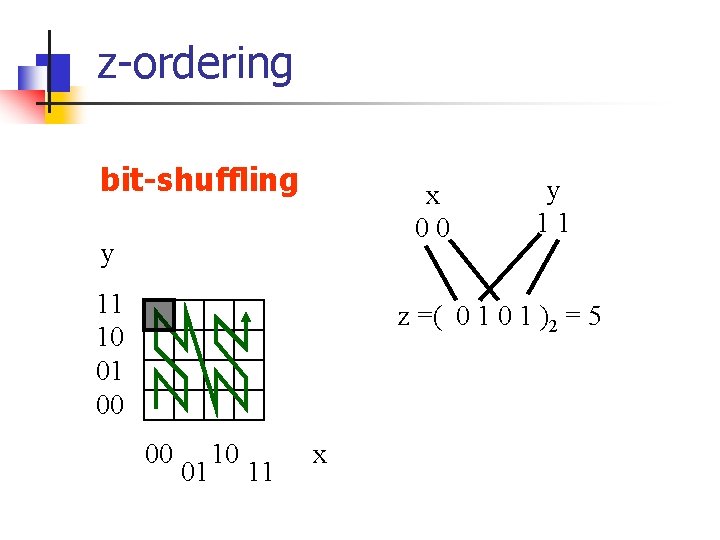
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 00 01 10 11 x

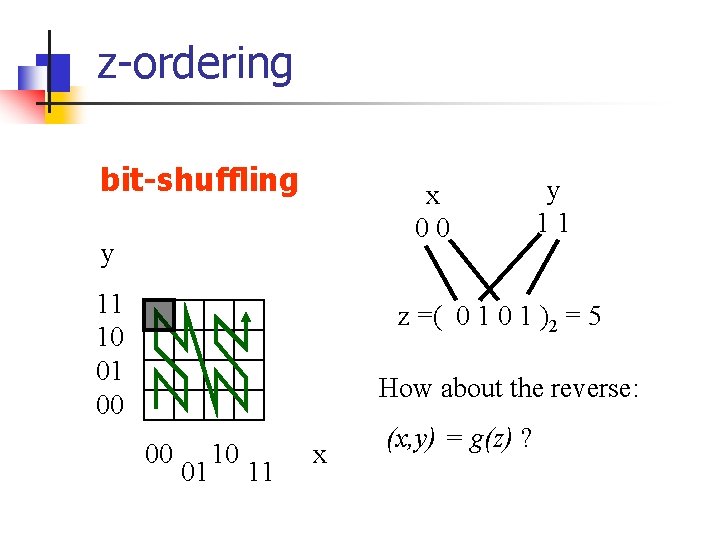
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 How about the reverse: 00 01 10 11 x (x, y) = g(z) ?

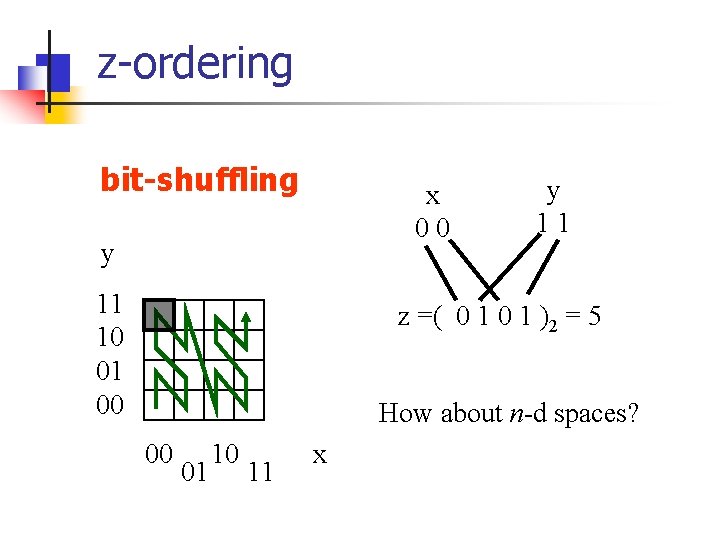
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 How about n-d spaces? 00 01 10 11 x

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers! Method #3?

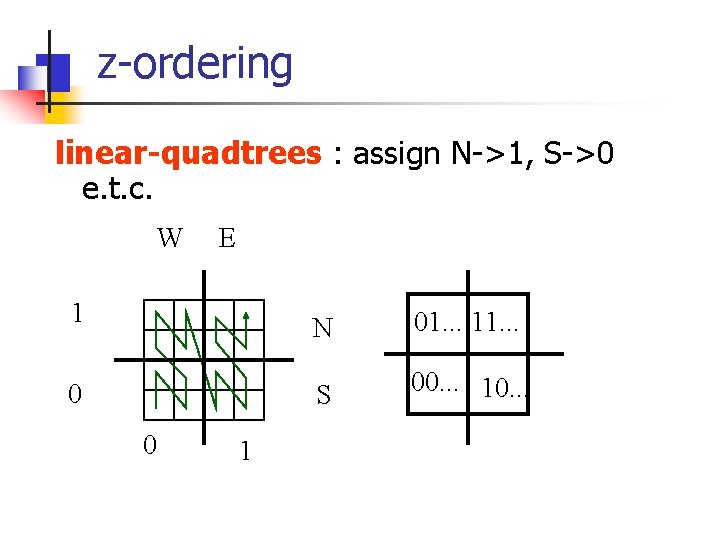
z-ordering linear-quadtrees : assign N->1, S->0 e. t. c. W E 1 0 0 1 N 01. . . 11. . . S 00. . . 10. . .

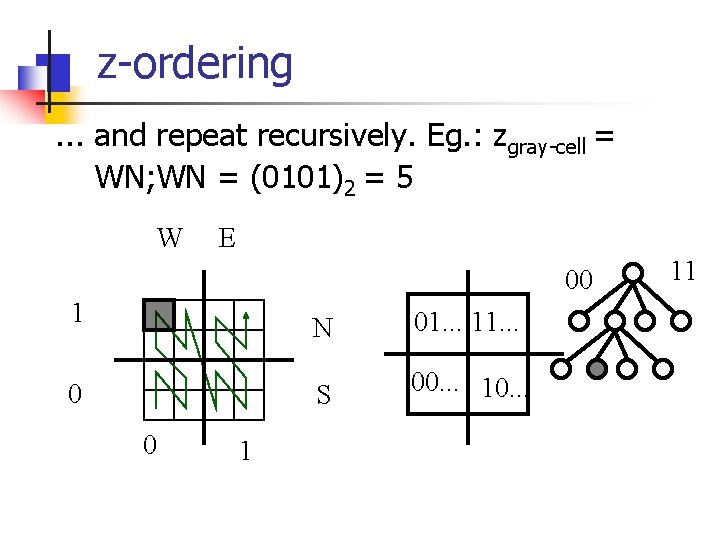
z-ordering. . . and repeat recursively. Eg. : zgray-cell = WN; WN = (0101)2 = 5 W E 00 1 0 0 1 N 01. . . 11. . . S 00. . . 10. . . 11

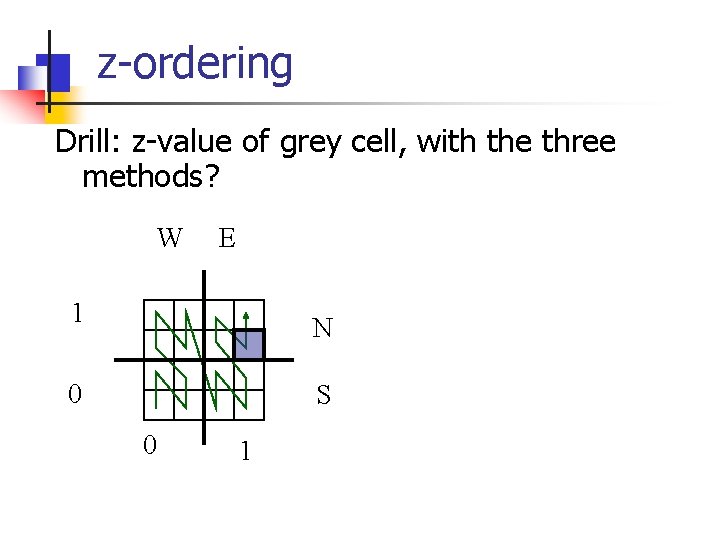
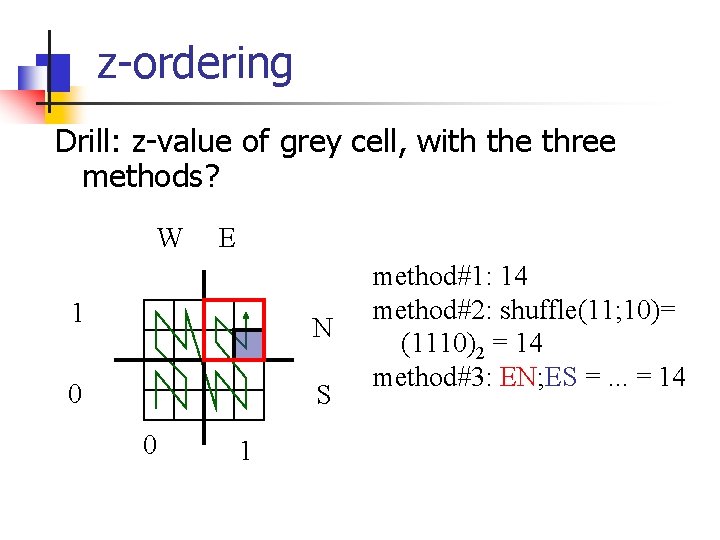
z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1

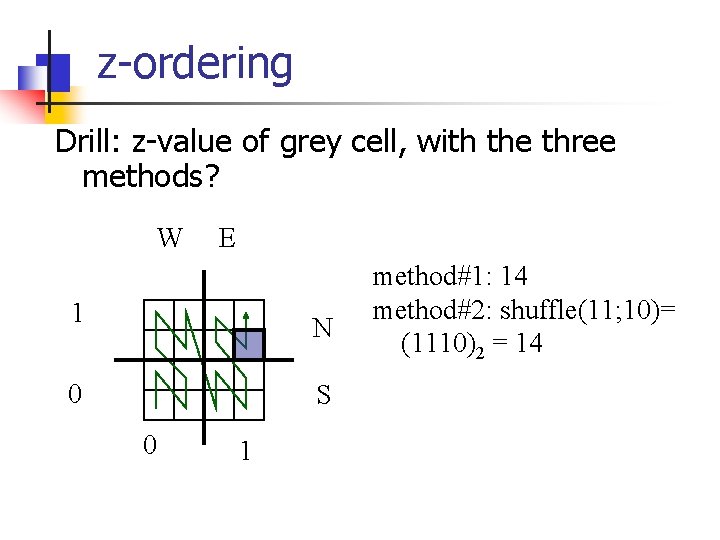
z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1 method#1: 14 method#2: shuffle(11; 10)= (1110)2 = 14

z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1 method#1: 14 method#2: shuffle(11; 10)= (1110)2 = 14 method#3: EN; ES =. . . = 14

z-ordering - Detailed outline n spatial access methods n z-ordering n n n main idea - 3 methods use w/ B-trees; algorithms (range, knn queries. . . ) non-point (eg. , region) data analysis; variations R-trees

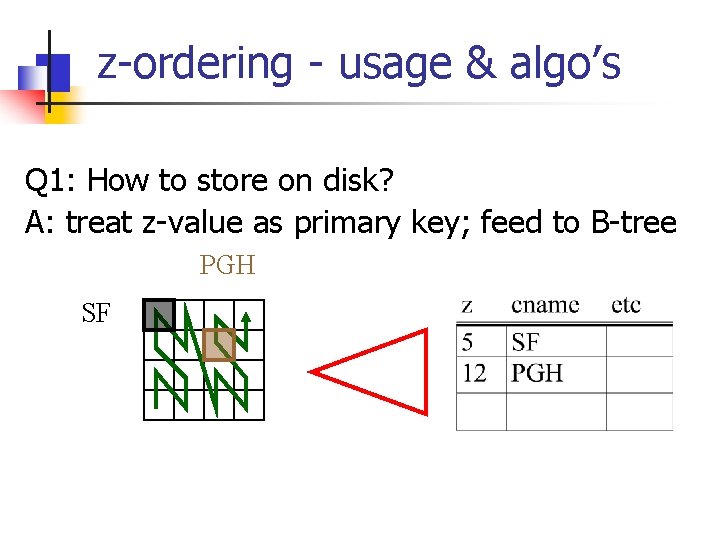
z-ordering - usage & algo’s Q 1: How to store on disk? A: Q 2: How to answer range queries etc

z-ordering - usage & algo’s Q 1: How to store on disk? A: treat z-value as primary key; feed to B-tree PGH SF

z-ordering - usage & algo’s MAJOR ADVANTAGES w/ B-tree: n already inside commercial systems (no coding /debugging!) n concurrency & recovery is ready PGH SF

z-ordering - Detailed outline n spatial access methods n z-ordering n n n main idea - 3 methods use w/ B-trees; algorithms (range, knn queries. . . ) non-point (eg. , region) data analysis; variations R-trees

z-ordering - variations Q: is z-ordering the best we can do?

z-ordering - variations Q: is z-ordering the best we can do? A: probably not - occasional long ‘jumps’ Q: then?

z-ordering - variations Q: is z-ordering the best we can do? A: probably not - occasional long ‘jumps’ Q: then? A 1: Gray codes

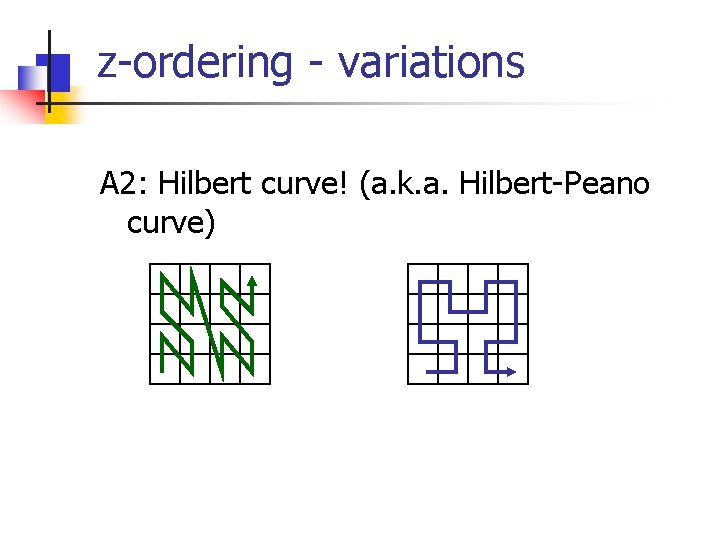
z-ordering - variations A 2: Hilbert curve! (a. k. a. Hilbert-Peano curve)

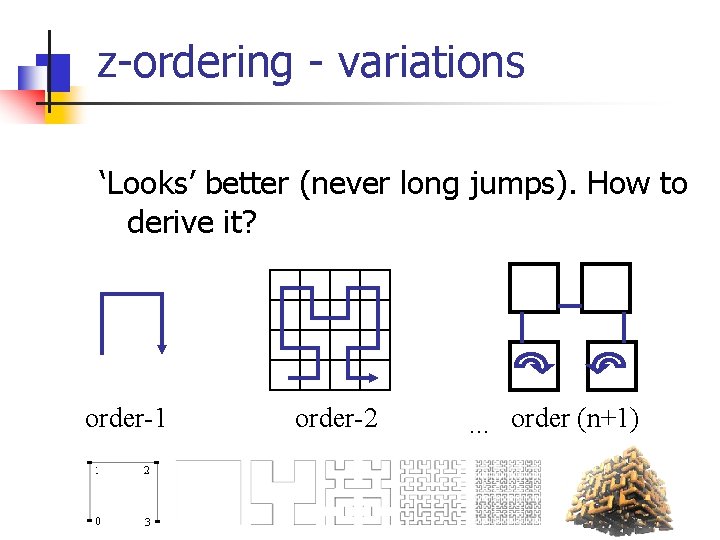
z-ordering - variations ‘Looks’ better (never long jumps). How to derive it?

z-ordering - variations ‘Looks’ better (never long jumps). How to derive it? order-1 order-2 . . . order (n+1)

z-ordering - variations Q: function for the Hilbert curve ( h = f(x, y) )? A: bit-shuffling, followed by post-processing, to account for rotations. Linear on # bits. See textbook, for pointers to code/algorithms (eg. , [Jagadish, 90])

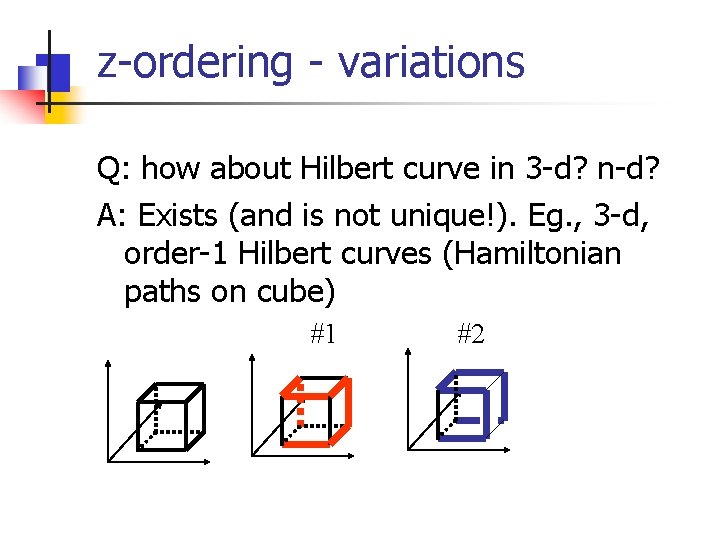
z-ordering - variations Q: how about Hilbert curve in 3 -d? n-d? A: Exists (and is not unique!). Eg. , 3 -d, order-1 Hilbert curves (Hamiltonian paths on cube) #1 #2

z-ordering - Detailed outline n spatial access methods n z-ordering n n n main idea - 3 methods use w/ B-trees; algorithms (range, knn queries. . . ) non-point (eg. , region) data analysis; variations R-trees. . .

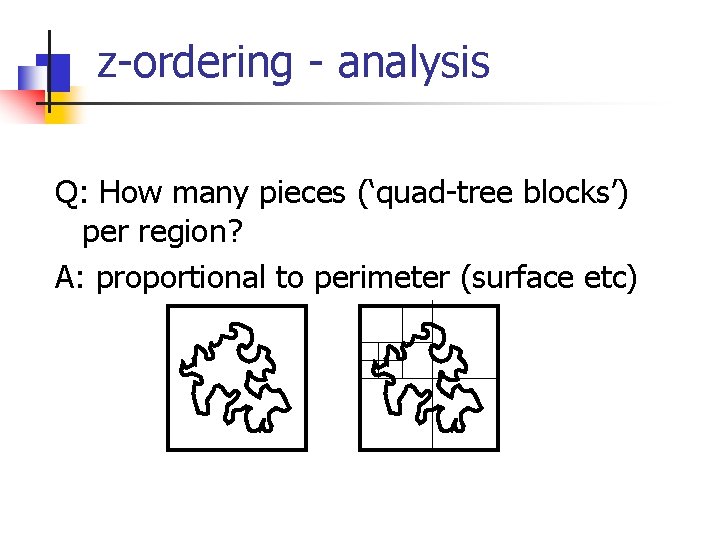
z-ordering - analysis Q: How many pieces (‘quad-tree blocks’) per region? A: proportional to perimeter (surface etc)

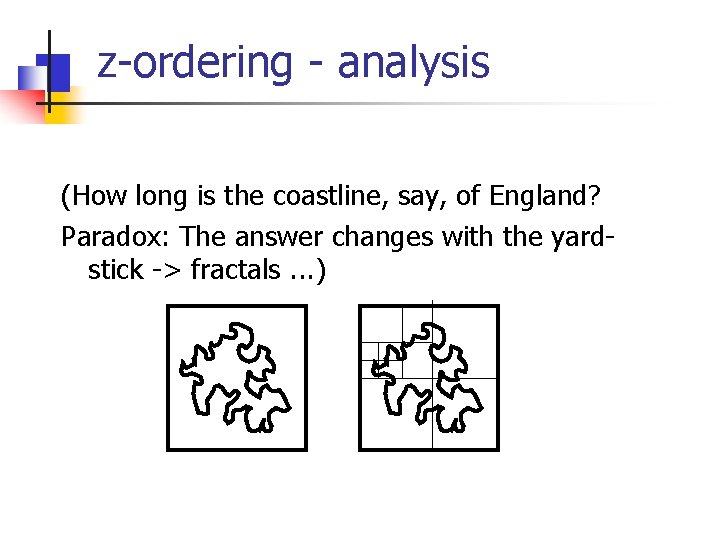
z-ordering - analysis (How long is the coastline, say, of England? Paradox: The answer changes with the yardstick -> fractals. . . )

z-ordering - analysis Q: Should we decompose a region to full detail (and store in B-tree)?

z-ordering - analysis Q: Should we decompose a region to full detail (and store in B-tree)? A: NO! approximation with 1 -3 pieces/zvalues is best [Orenstein 90]

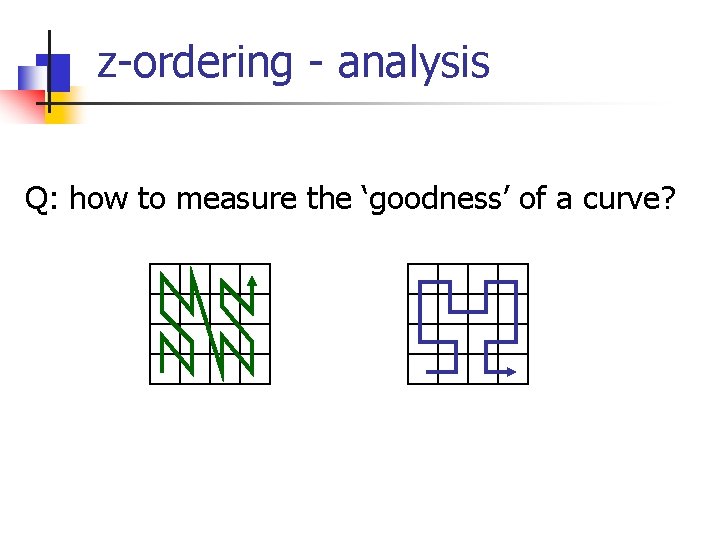
z-ordering - analysis Q: how to measure the ‘goodness’ of a curve?

z-ordering - analysis Q: how to measure the ‘goodness’ of a curve? A: e. g. , avg. # of runs, for range queries 4 runs 3 runs (#runs ~ #disk accesses on B-tree)

z-ordering - analysis Q: So, is Hilbert really better? A: 27% fewer runs, for 2 -d (similar for 3 -d) Q: are there formulas for #runs, #of quadtree blocks etc? A: Yes ([Jagadish; Moon+ etc] see textbook)

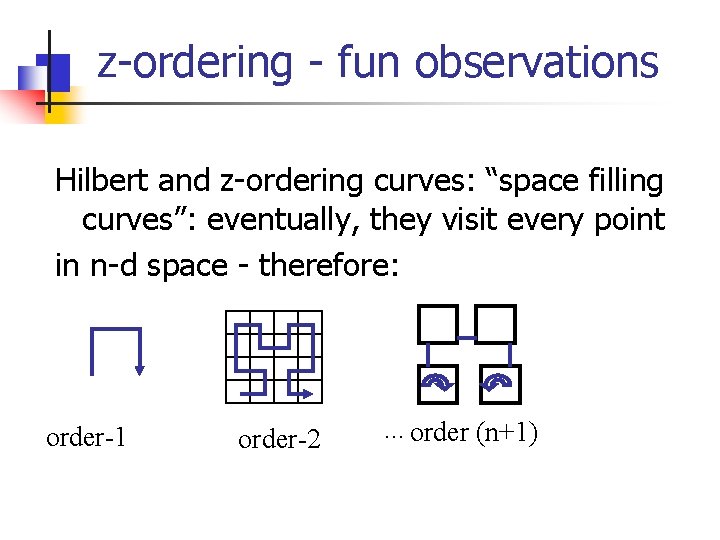
z-ordering - fun observations Hilbert and z-ordering curves: “space filling curves”: eventually, they visit every point in n-d space - therefore: order-1 order-2 . . . order (n+1)

z-ordering - fun observations. . . they show that the plane has as many points as a line (-> headaches for 1900’s mathematics/topology). (fractals, again!) order-1 order-2 . . . order (n+1)

z-ordering - fun observations Observation #2: Hilbert (like) curve for video encoding [Y. Matias+, CRYPTO ‘ 87]: Given a frame, visit its pixels in randomized hilbert order; compress; and transmit

z-ordering - fun observations In general, Hilbert curve is great for preserving distances, clustering, vector quantization etc

Conclusions n n n z-ordering is a great idea (n-d points -> 1 -d points; feed to B-trees) used by TIGER system and (most probably) by other GIS products works great with low-dim points

SAMs – Detailed Outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

SAMs - more detailed outline n R-trees n n n main idea; file structure (algorithms: insertion/split) (deletion) (search: range, nn, spatial joins) variations (packed; hilbert; . . . )

R-trees n n n z-ordering: cuts regions to pieces -> dup. elim. how could we avoid that? Idea: Minimum Bounding Rectangles
![Rtrees n Guttman 84 Main idea allow parents to overlap n n n R-trees n [Guttman 84] Main idea: allow parents to overlap! n n n =>](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-96.jpg)
R-trees n [Guttman 84] Main idea: allow parents to overlap! n n n => guaranteed 50% utilization => easier insertion/split algorithms. (only deal with Minimum Bounding Rectangles - MBRs)

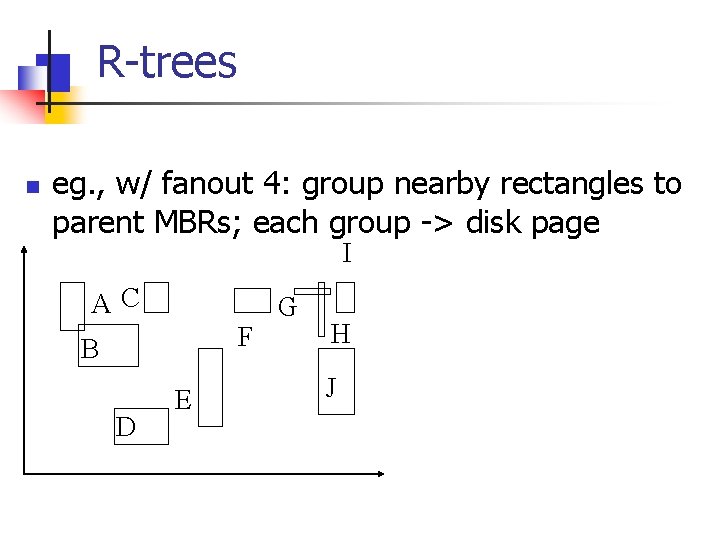
R-trees n eg. , w/ fanout 4: group nearby rectangles to parent MBRs; each group -> disk page I AC F B D E G H J

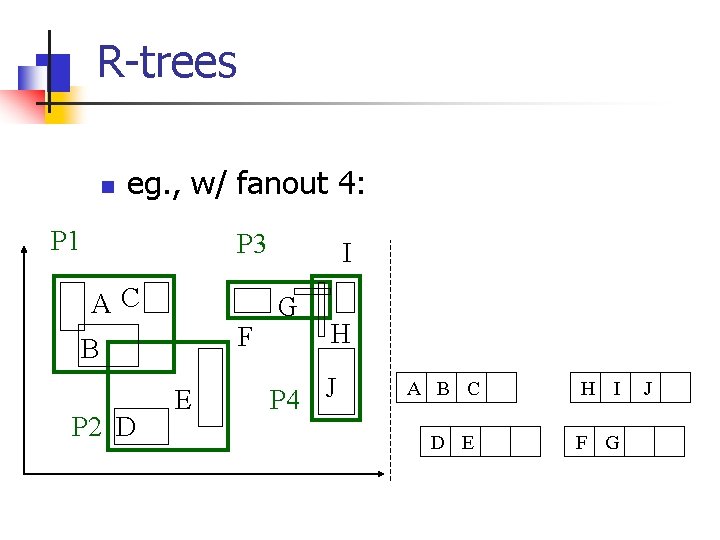
R-trees n eg. , w/ fanout 4: P 1 P 3 AC F B P 2 D E I G H P 4 J A B C D E H I F G J

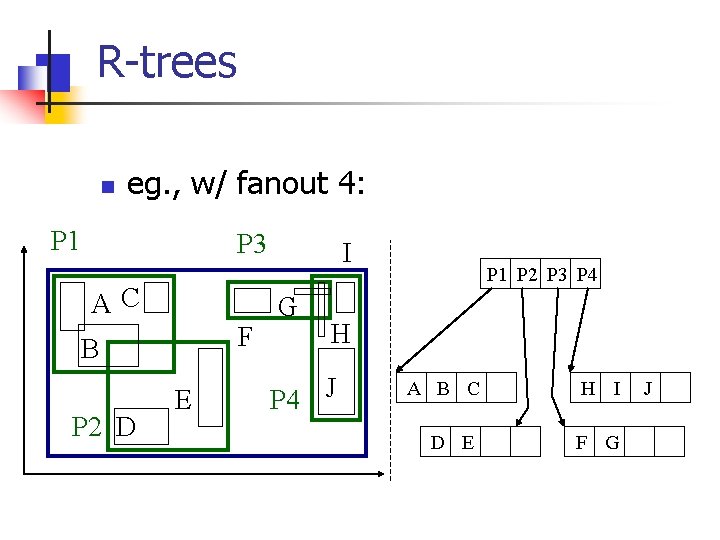
R-trees n eg. , w/ fanout 4: P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

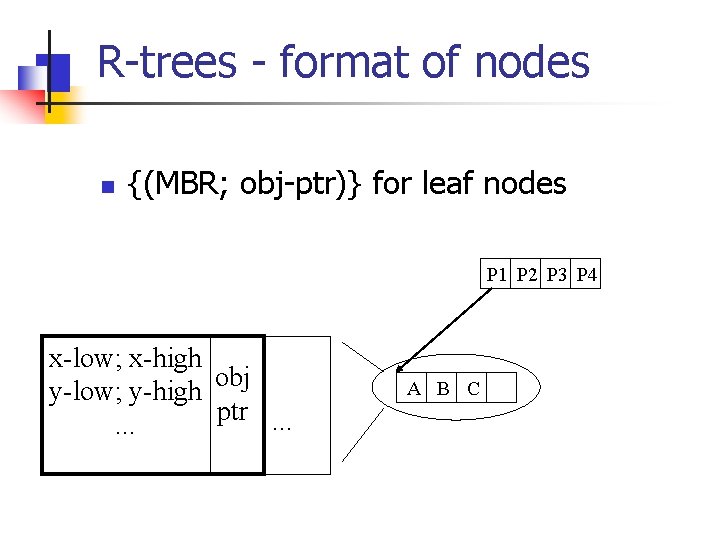
R-trees - format of nodes n {(MBR; obj-ptr)} for leaf nodes P 1 P 2 P 3 P 4 x-low; x-high obj y-low; y-high ptr. . . A B C

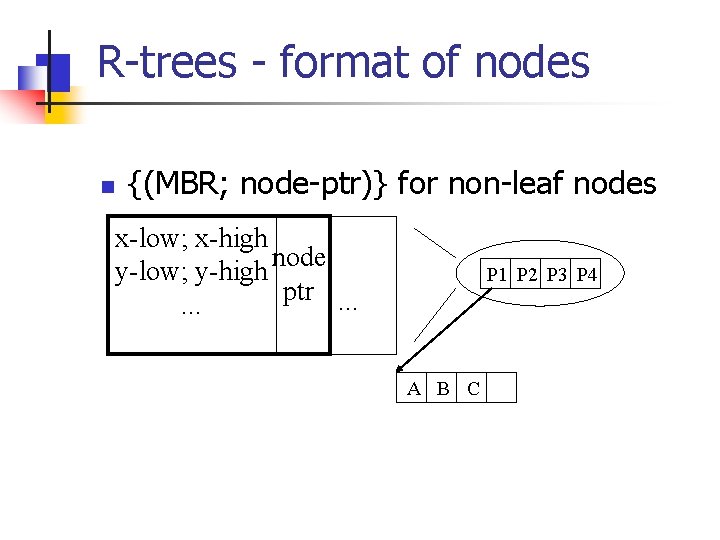
R-trees - format of nodes n {(MBR; node-ptr)} for non-leaf nodes x-low; x-high node y-low; y-high ptr. . . P 1 P 2 P 3 P 4 A B C

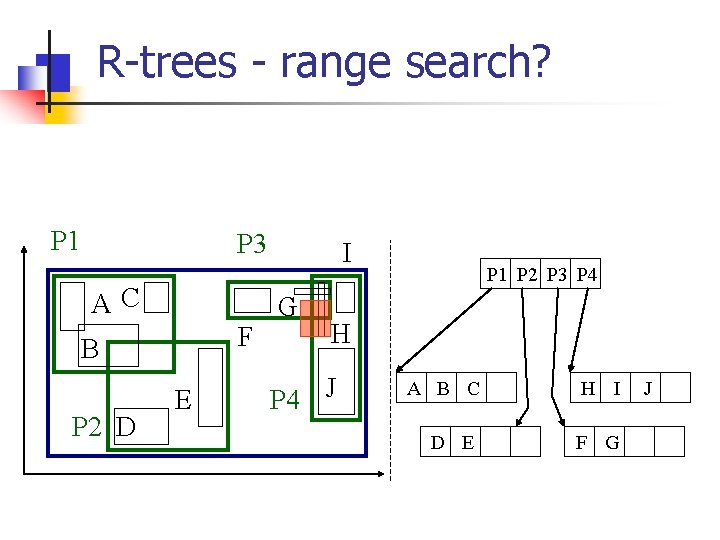
R-trees - range search? P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

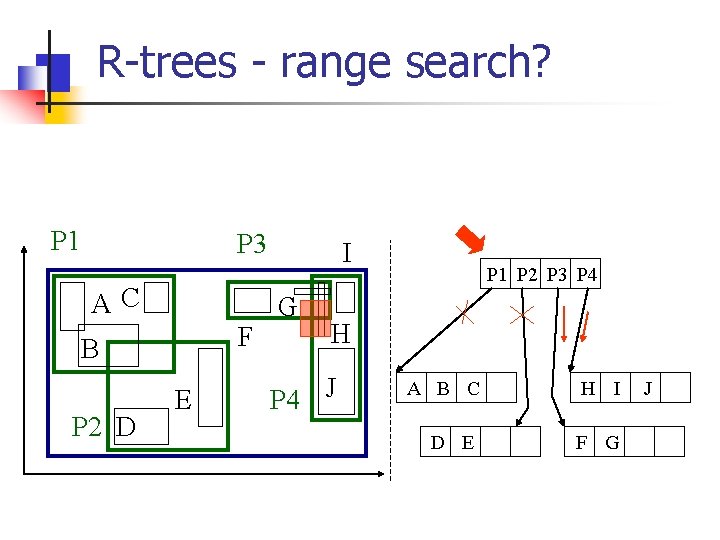
R-trees - range search? P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

R-trees - range search Observations: n every parent node completely covers its ‘children’ n a child MBR may be covered by more than one parent - it is stored under ONLY ONE of them. (i. e. , no need for dup. elim. ) n a point query may follow multiple branches. n everything works for any dimensionality

SAMs - more detailed outline n R-trees n n n main idea; file structure algorithms: insertion/split deletion search: range, nn, spatial joins performance analysis variations (packed; hilbert; . . . )

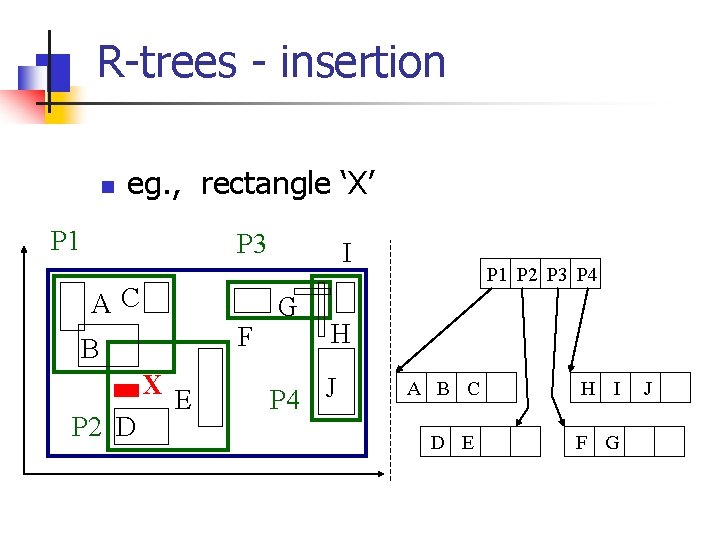
R-trees - insertion n eg. , rectangle ‘X’ P 1 P 3 AC F B X P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

R-trees - insertion n eg. , rectangle ‘X’ P 1 P 3 AC F B X P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E X H I F G J

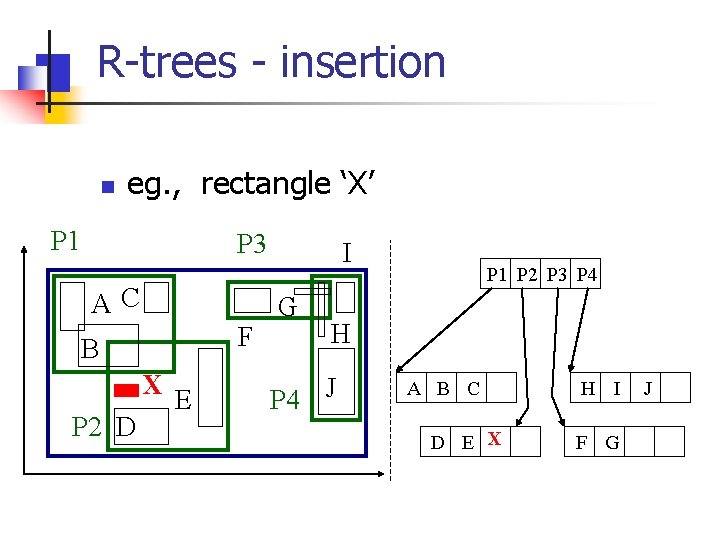
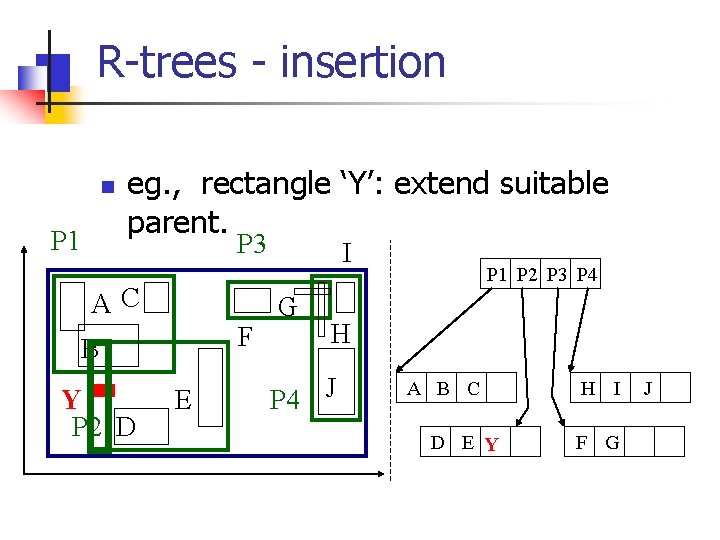
R-trees - insertion n eg. , rectangle ‘Y’ P 1 P 3 AC F B Y P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

R-trees - insertion n P 1 eg. , rectangle ‘Y’: extend suitable parent. P 3 AC F B Y P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E Y H I F G J

R-trees - insertion n n eg. , rectangle ‘Y’: extend suitable parent. Q: how to measure ‘suitability’?

R-trees - insertion n n eg. , rectangle ‘Y’: extend suitable parent. Q: how to measure ‘suitability’? A: by increase in area (volume) (more details: later, under ‘performance analysis’) Q: what if there is no room? how to split?

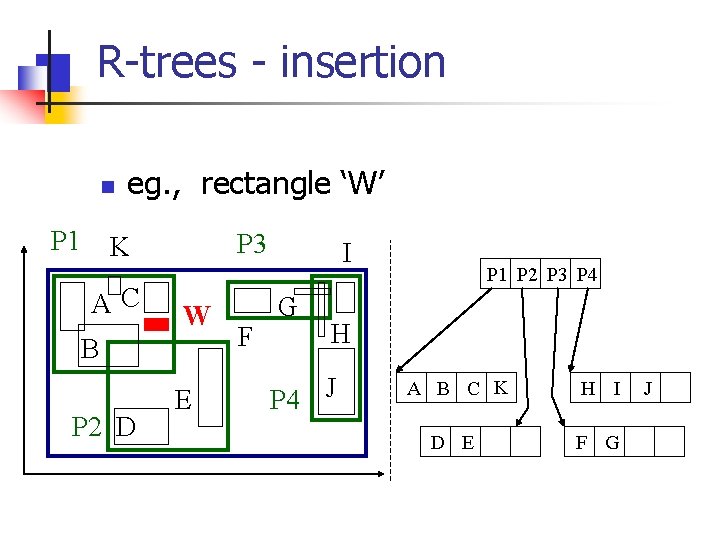
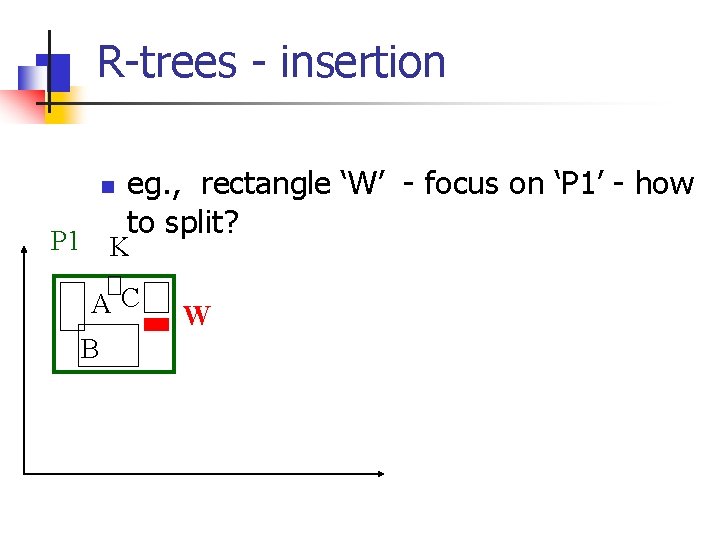
R-trees - insertion n P 1 eg. , rectangle ‘W’ P 3 K AC W B P 2 D E F I G P 1 P 2 P 3 P 4 H P 4 J A B C K H I D E F G J

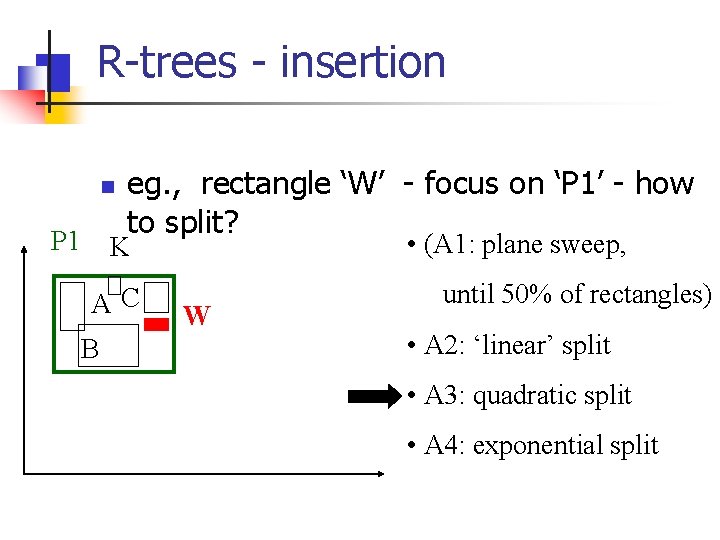
R-trees - insertion n P 1 eg. , rectangle ‘W’ - focus on ‘P 1’ - how to split? K AC B W

R-trees - insertion n P 1 eg. , rectangle ‘W’ - focus on ‘P 1’ - how to split? • (A 1: plane sweep, K AC B W until 50% of rectangles) • A 2: ‘linear’ split • A 3: quadratic split • A 4: exponential split

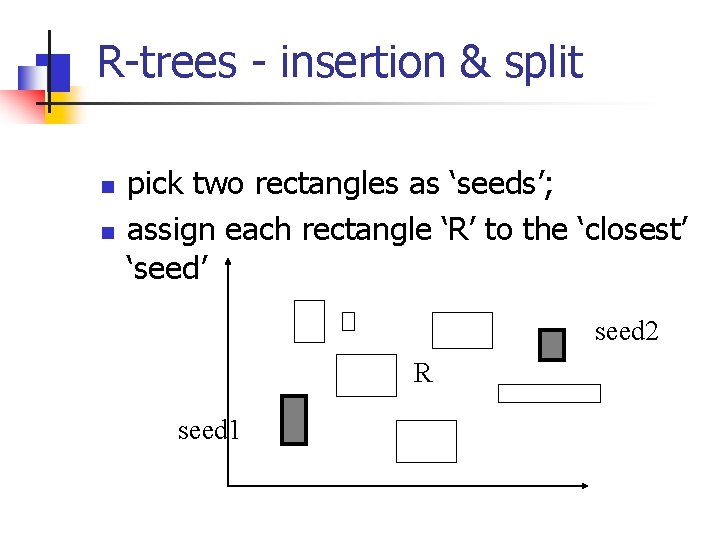
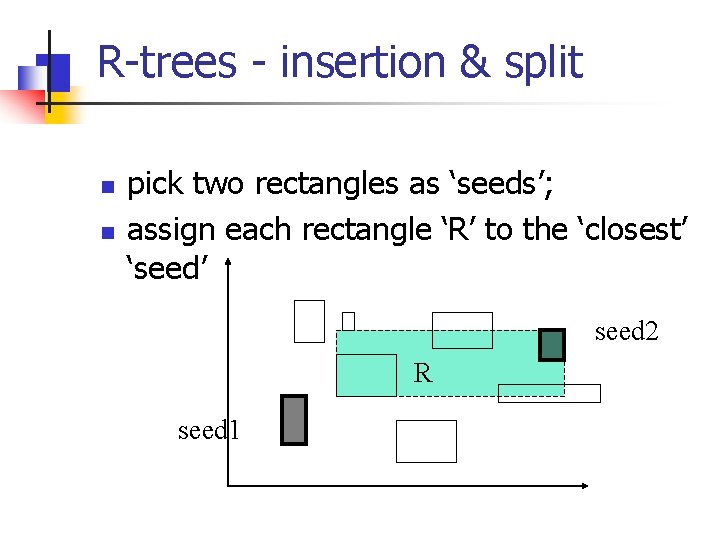
R-trees - insertion & split n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ seed 2 R seed 1

R-trees - insertion & split n n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ Q: how to measure ‘closeness’?

R-trees - insertion & split n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ Q: how to measure ‘closeness’? A: by increase of area (volume)

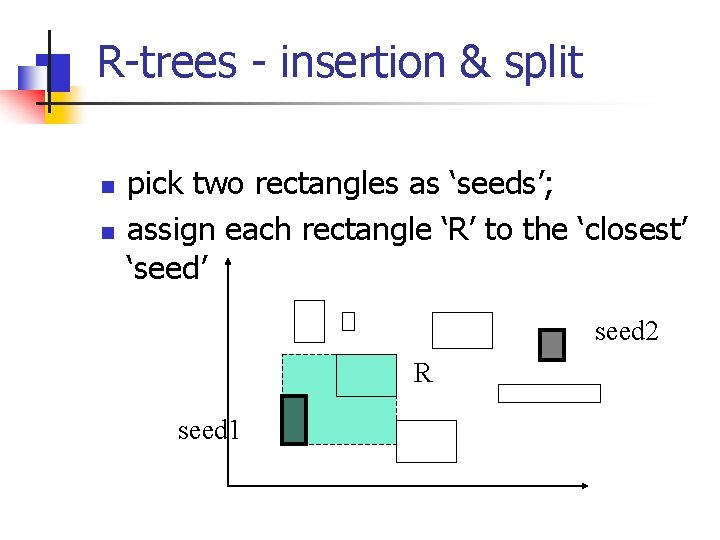
R-trees - insertion & split n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ seed 2 R seed 1

R-trees - insertion & split n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ seed 2 R seed 1

R-trees - insertion & split n n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ smart idea: pre-sort rectangles according to delta of closeness (ie. , schedule easiest choices first!)

R-trees - insertion - pseudocode n n decide which parent to put new rectangle into (‘closest’ parent) if overflow, split to two, using (say, ) the quadratic split algorithm n n propagate the split upwards, if necessary update the MBRs of the affected parents.

R-trees - insertion - observations n many more split algorithms exist (next!)

SAMs - more detailed outline n R-trees n n n main idea; file structure algorithms: insertion/split deletion search: range, nn, spatial joins performance analysis variations (packed; hilbert; . . . )

R-trees - deletion n n delete rectangle if underflow n ? ?

R-trees - deletion n n delete rectangle if underflow n n n temporarily delete all siblings (!); delete the parent node and re-insert them

SAMs - more detailed outline n R-trees n n n main idea; file structure algorithms: insertion/split deletion search: range, nn, spatial joins performance analysis variations (packed; hilbert; . . . )

R-trees - range search pseudocode: check the root for each branch, if its MBR intersects the query rectangle apply range-search (or print out, if this is a leaf)

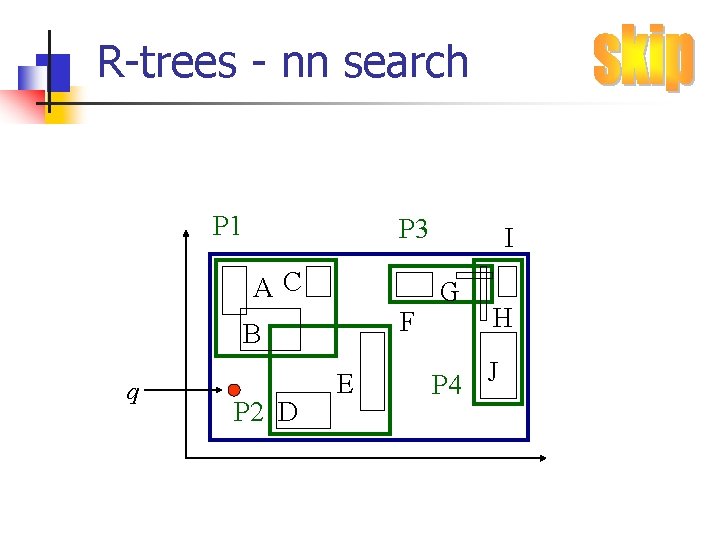
R-trees - nn search P 1 P 3 AC F B q P 2 D E I G H P 4 J

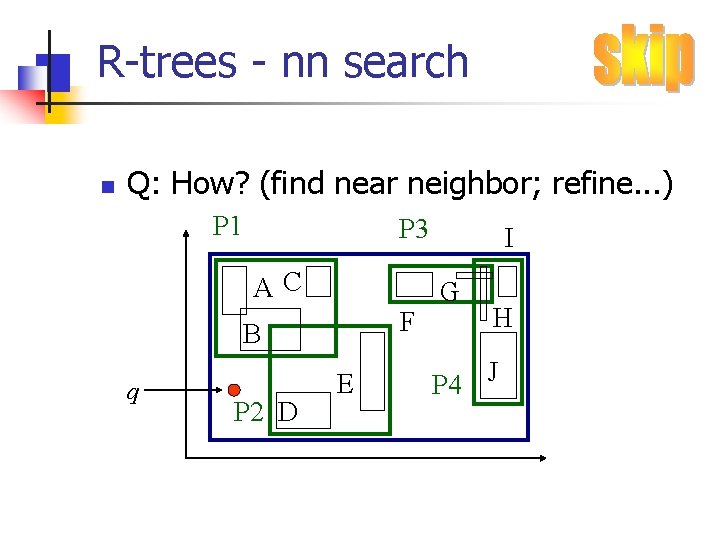
R-trees - nn search n Q: How? (find near neighbor; refine. . . ) P 1 P 3 AC F B q P 2 D E I G H P 4 J

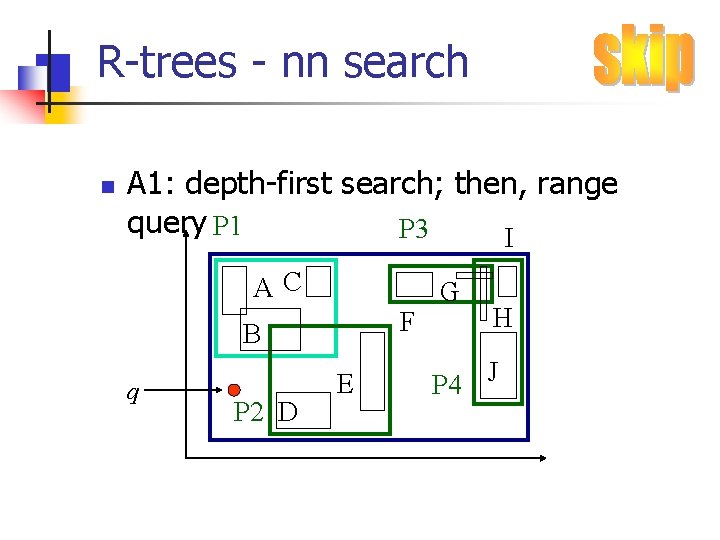
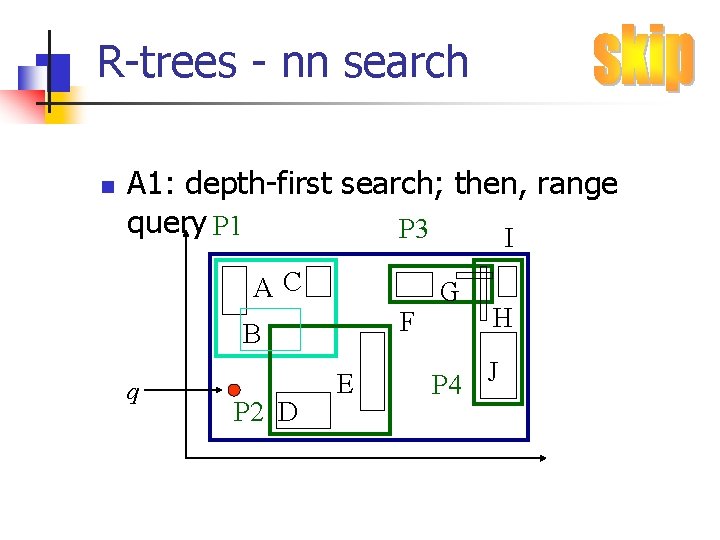
R-trees - nn search n A 1: depth-first search; then, range query P 1 P 3 I AC F B q P 2 D E G H P 4 J

R-trees - nn search n A 1: depth-first search; then, range query P 1 P 3 I AC F B q P 2 D E G H P 4 J

R-trees - nn search n A 1: depth-first search; then, range query P 1 P 3 AC F B q P 2 D E I G H P 4 J
![Rtrees nn search n A 2 Roussopoulos sigmod 95 n n priority queue R-trees - nn search n A 2: [Roussopoulos+, sigmod 95]: n n priority queue,](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-133.jpg)
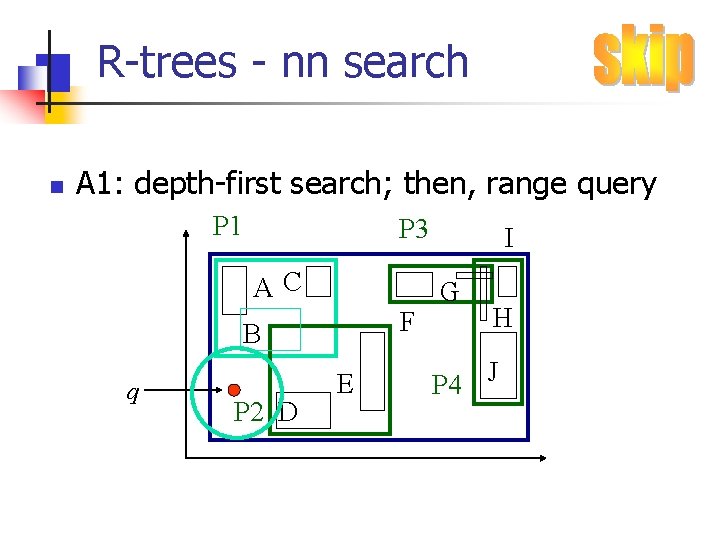
R-trees - nn search n A 2: [Roussopoulos+, sigmod 95]: n n priority queue, with promising MBRs, and their best and worst-case distance main idea:

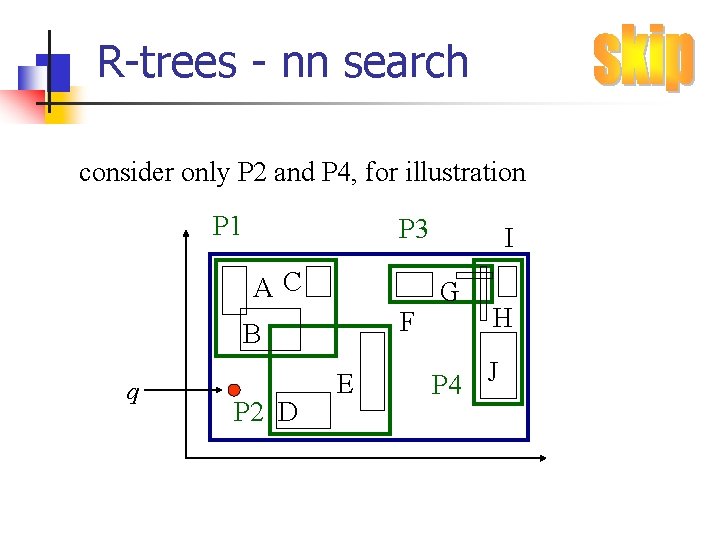
R-trees - nn search consider only P 2 and P 4, for illustration P 1 P 3 AC F B q P 2 D E I G H P 4 J

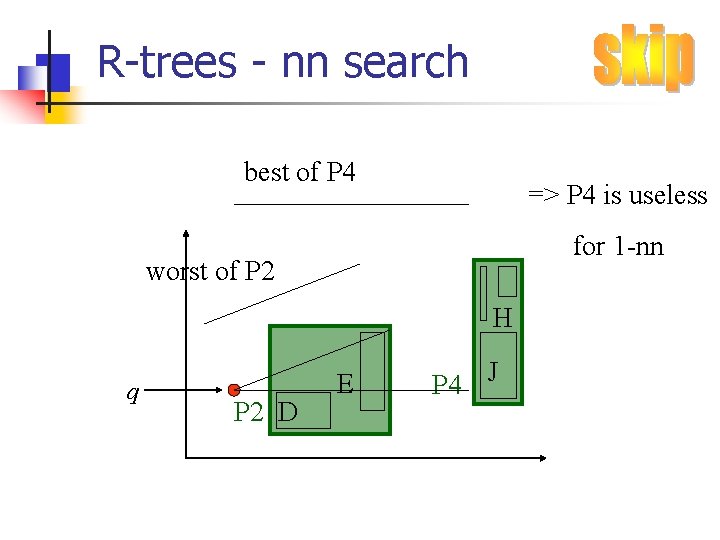
R-trees - nn search best of P 4 => P 4 is useless for 1 -nn worst of P 2 H q P 2 D E P 4 J

R-trees - nn search n what is really the worst of, say, P 2? worst of P 2 q P 2 D E

R-trees - nn search n n what is really the worst of, say, P 2? A: the smallest of the two red segments! q P 2
![Rtrees nn search n variations Hjaltason Samet incremental nn n n build R-trees - nn search n variations: [Hjaltason & Samet] incremental nn: n n build](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-138.jpg)
R-trees - nn search n variations: [Hjaltason & Samet] incremental nn: n n build a priority queue scan enough of the tree, to make sure you have the k nn to find the (k+1)-th, check the queue, and scan some more of the tree ‘optimal’ (but, may need too much memory)

SAMs - more detailed outline n R-trees n n n main idea; file structure algorithms: insertion/split deletion search: range, nn, spatial joins performance analysis variations (packed; hilbert; . . . )

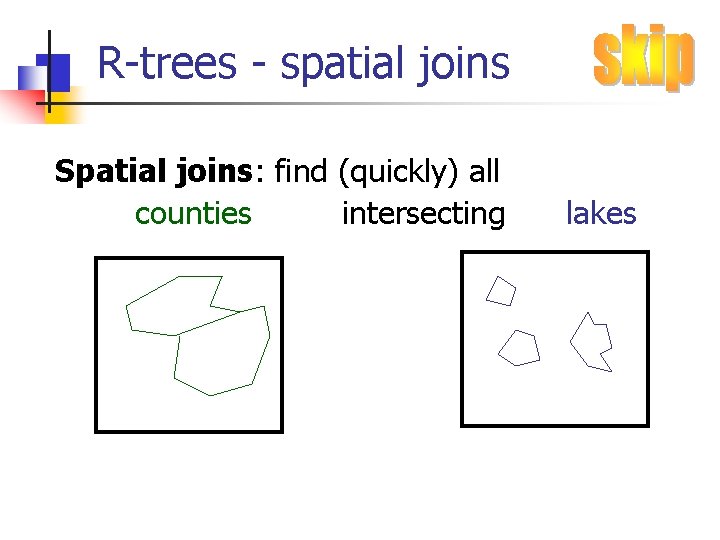
R-trees - spatial joins Spatial joins: find (quickly) all counties intersecting lakes

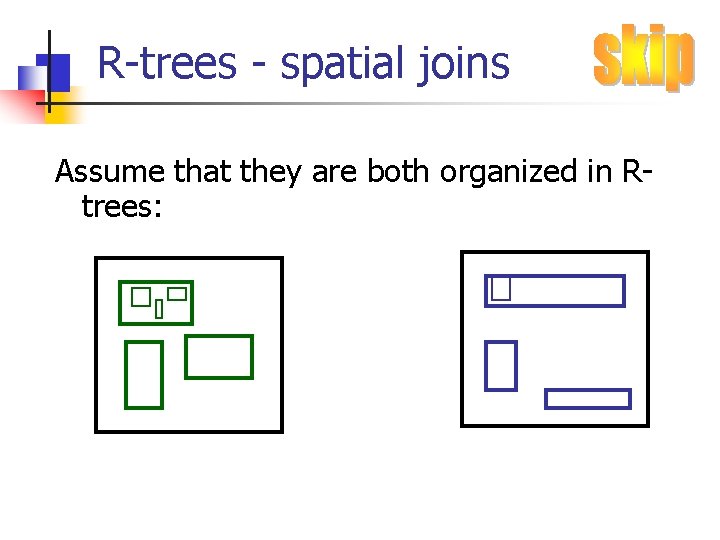
R-trees - spatial joins Assume that they are both organized in Rtrees:

R-trees - spatial joins for each parent P 1 of tree T 1 for each parent P 2 of tree T 2 if their MBRs intersect, process them recursively (ie. , check their children)
![Rtrees spatial joins Improvements variations Seeger sigmod 92 do some prefiltering R-trees - spatial joins Improvements - variations: - [Seeger+, sigmod 92]: do some pre-filtering;](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-143.jpg)
R-trees - spatial joins Improvements - variations: - [Seeger+, sigmod 92]: do some pre-filtering; do plane-sweeping to avoid N 1 * N 2 tests for intersection - [Lo & Ravishankar, sigmod 94]: ‘seeded’ R-trees (FYI, many more papers on spatial joins, without R-trees: [Koudas+ Sevcik], e. t. c. )

SAMs - more detailed outline n R-trees n n n main idea; file structure algorithms: insertion/split deletion search: range, nn, spatial joins variations (packed; hilbert; . . . )

R-trees - variations Guttman’s R-trees sparked much follow-up work n can we do better splits? n what about static datasets (no ins/del/upd)? n what about other bounding shapes?

R-trees - variations Guttman’s R-trees sparked much follow-up work n can we do better splits? n i. e, defer splits?
![Rtrees variations A Rtrees Kriegel SIGMOD 90 n defer splits by forcedreinsert i R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i.](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-147.jpg)
R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i. e. : instead of splitting, temporarily delete some entries, shrink overflowing MBR, and re-insert those entries n Which ones to re-insert? n How many?
![Rtrees variations A Rtrees Kriegel SIGMOD 90 n defer splits by forcedreinsert i R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i.](https://slidetodoc.com/presentation_image_h2/69c4d74c860c03ea6ab4cdddde4ff161/image-148.jpg)
R-trees - variations A: R*-trees [Kriegel+, SIGMOD 90] n defer splits, by forced-reinsert, i. e. : instead of splitting, temporarily delete some entries, shrink overflowing MBR, and re-insert those entries n Which ones to re-insert? n How many? A: 30%

R-trees - variations Q: Other ways to defer splits?

R-trees - variations Q: Other ways to defer splits? A: Push a few keys to the closest sibling node (closest = ? ? )

R-trees - variations R*-trees: Also try to minimize area AND perimeter, in their split. Performance: higher space utilization; faster than plain R-trees. One of the most successful R-tree variants.

R-trees - variations Guttman’s R-trees sparked much follow-up work n can we do better splits? n what about static datasets (no ins/del/upd)? n n Hilbert R-trees what about other bounding shapes?

R-trees - variations n n what about static datasets (no ins/del/upd)? Q: Best way to pack points?

R-trees - variations n n n what about static datasets (no ins/del/upd)? Q: Best way to pack points? A 1: plane-sweep great for queries on ‘x’; terrible for ‘y’

R-trees - variations n n n what about static datasets (no ins/del/upd)? Q: Best way to pack points? A 1: plane-sweep great for queries on ‘x’; bad for ‘y’

R-trees - variations n n what about static datasets (no ins/del/upd)? Q: Best way to pack points? A 1: plane-sweep great for queries on ‘x’; terrible for ‘y’ Q: how to improve?

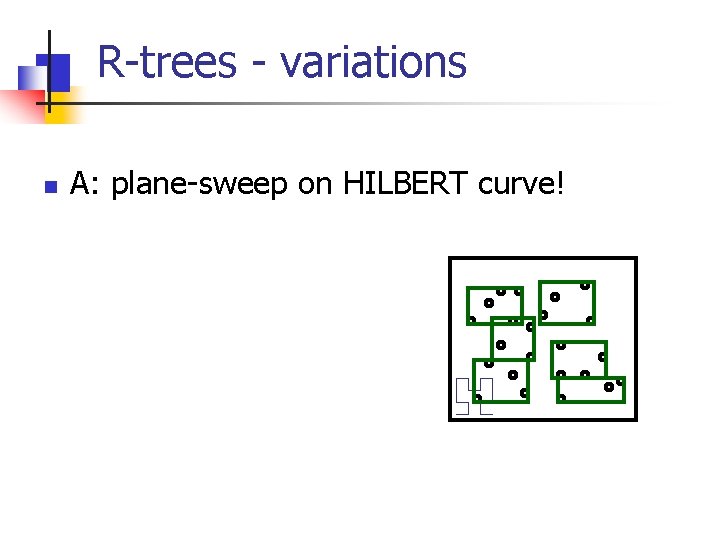
R-trees - variations n A: plane-sweep on HILBERT curve!

R-trees - variations n n n A: plane-sweep on HILBERT curve! In fact, it can be made dynamic (how? ), as well as to handle regions (how? ) A: [Kamel+, VLDB 94]

R-trees - variations Guttman’s R-trees sparked much follow-up work n can we do better splits? n what about static datasets (no ins/del/upd)? n what about other bounding shapes?

R-trees - variations n n n what about other bounding shapes? (and why? ) A 1: arbitrary-orientation lines (cell-tree, [Guenther] A 2: P-trees (polygon trees) (MB polygon: 0, 90, 45, 135 degree lines)

R-trees - variations n n n A 3: L-shapes; holes (h. B-tree) A 4: TV-trees [Lin+, VLDB-Journal 1994] A 5: SR-trees [Katayama+, SIGMOD 97] (used in Informedia)

R-trees - conclusions n n n Popular method; like multi-d B-trees guaranteed utilization good search times (for low-dim. at least) R*-, Hilbert- and SR-trees: still used IBM (Informix) ships Data. Blade with R-trees

References n n n Guttman, A. (June 1984). R-Trees: A Dynamic Index Structure for Spatial Searching. Proc. ACM SIGMOD, Boston, Mass. Jagadish, H. V. (May 23 -25, 1990). Linear Clustering of Objects with Multiple Attributes. ACM SIGMOD Conf. , Atlantic City, NJ. Lin, K. -I. , H. V. Jagadish, et al. (Oct. 1994). “The TVtree - An Index Structure for High-dimensional Data. ” VLDB Journal 3: 517 -542.

References, cont’d n n n Pagel, B. , H. Six, et al. (May 1993). Towards an Analysis of Range Query Performance. Proc. of ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems (PODS), Washington, D. C. Robinson, J. T. (1981). The k-D-B-Tree: A Search Structure for Large Multidimensional Dynamic Indexes. Proc. ACM SIGMOD. Roussopoulos, N. , S. Kelley, et al. (May 1995). Nearest Neighbor Queries. Proc. of ACM-SIGMOD, San Jose, CA.
 Temple university cis
Temple university cis Erth 616
Erth 616 Indicatori di anomalia provvedimento 616 del 2010
Indicatori di anomalia provvedimento 616 del 2010 Cis temple
Cis temple Temple for business success
Temple for business success Temple university environmental engineering
Temple university environmental engineering Temple university irb
Temple university irb Drs temple university
Drs temple university Study abroad application temple
Study abroad application temple Temple university ielp
Temple university ielp Nsf cise msi
Nsf cise msi Temple isss
Temple isss Temple university dba
Temple university dba Oneness university temple
Oneness university temple Aarononpc
Aarononpc Temple university undergraduate bulletin
Temple university undergraduate bulletin Dept nmr spectroscopy
Dept nmr spectroscopy Fl dept of agriculture
Fl dept of agriculture Finance departments
Finance departments Worcester ma building dept
Worcester ma building dept Dept. name of organization (of affiliation)
Dept. name of organization (of affiliation) Mn dept of education
Mn dept of education Dept of finance and administration
Dept of finance and administration Dept. name of organization
Dept. name of organization Employment first ohio
Employment first ohio Dept. name of organization (of affiliation)
Dept. name of organization (of affiliation) Vaginal dept
Vaginal dept Gome dept
Gome dept Gome dept
Gome dept Gome dept
Gome dept Gome dept
Gome dept Hoe dept
Hoe dept Lafd interview score
Lafd interview score Maine dept of agriculture
Maine dept of agriculture Dept of education
Dept of education Florida dept of agriculture and consumer services
Florida dept of agriculture and consumer services Florida dept of agriculture and consumer services
Florida dept of agriculture and consumer services Dept a
Dept a Central islip fire dept
Central islip fire dept Rowan county social services
Rowan county social services Dept of education
Dept of education Tabella chemical shift c13
Tabella chemical shift c13 Pt dept logistik
Pt dept logistik Nys dept of homeland security
Nys dept of homeland security Affiliate disclodures
Affiliate disclodures La geaux biz
La geaux biz Rewley house continuing education library
Rewley house continuing education library Nebraska dept of agriculture
Nebraska dept of agriculture Iit
Iit Dept ind onegov
Dept ind onegov Albany county dept of social services
Albany county dept of social services 詹景裕
詹景裕 Dimensions of solomon's temple
Dimensions of solomon's temple Tuid temple
Tuid temple Salt lake temple baptismal font
Salt lake temple baptismal font Temple os
Temple os Temple of bacchus plan
Temple of bacchus plan Temple of bacchus plan
Temple of bacchus plan Temple data analytics challenge
Temple data analytics challenge Ward temple and family history leader
Ward temple and family history leader Temple accounts format
Temple accounts format Lean temple
Lean temple Peripteral plan
Peripteral plan Maths in indian architecture
Maths in indian architecture Temple fay technique
Temple fay technique Triglif
Triglif Temple grec plan
Temple grec plan Don't you know that your body is the temple
Don't you know that your body is the temple Foguang si pagoda
Foguang si pagoda Hindu temple tempe
Hindu temple tempe Parts of a greek temple
Parts of a greek temple My drs temple
My drs temple Tuportal
Tuportal Dali seven wonders of the world
Dali seven wonders of the world Ephraim temple
Ephraim temple John stanley temple
John stanley temple Ellen cohn yale
Ellen cohn yale Lean temple
Lean temple Elijah kirtland temple
Elijah kirtland temple Reading hindu temple
Reading hindu temple Ahet aton
Ahet aton Doomsday book
Doomsday book Draper temple prayer roll
Draper temple prayer roll Rushing wind blow through this temple
Rushing wind blow through this temple Temple grec rond
Temple grec rond Timpanogos temple prayer roll
Timpanogos temple prayer roll Temple noble art
Temple noble art Temple data analytics challenge
Temple data analytics challenge Temple hsc library
Temple hsc library White temple and ziggurat
White temple and ziggurat Millennial temple
Millennial temple Temple architecture of himachal pradesh
Temple architecture of himachal pradesh Lean temple
Lean temple Bull temple
Bull temple Power point temple
Power point temple What is mid term break by seamus heaney about
What is mid term break by seamus heaney about Udvada parsi temple
Udvada parsi temple Isaac gottlieb temple
Isaac gottlieb temple Hindu temple augusta ga
Hindu temple augusta ga Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple By the waters of babylon stephen vincent benet
By the waters of babylon stephen vincent benet Inca sun temple of cuzco ap world history
Inca sun temple of cuzco ap world history Contoh announcement study tour
Contoh announcement study tour Presentation in the temple
Presentation in the temple Peplos kore
Peplos kore Zaha temple
Zaha temple Mansa musa temple
Mansa musa temple Jain center of greater boston
Jain center of greater boston Example of indo aryan jain temple is
Example of indo aryan jain temple is Temple grafton primary school
Temple grafton primary school Lean temple
Lean temple Mamandur cave temple
Mamandur cave temple Jie wu
Jie wu Apollo temple
Apollo temple Bhaskara haripriya
Bhaskara haripriya Daguerre boulevard du temple
Daguerre boulevard du temple Who guards olympus
Who guards olympus Spring temple buddha
Spring temple buddha Jasper johns map 1963
Jasper johns map 1963 Kuehne nagel savigny le temple
Kuehne nagel savigny le temple A pyramid-shaped temple tower
A pyramid-shaped temple tower Lean temple
Lean temple Lean temple
Lean temple Robert temple fda
Robert temple fda Tigawa temple plan
Tigawa temple plan Temple bible church
Temple bible church Elementos liricos
Elementos liricos Solomon finished the temple
Solomon finished the temple Solomon finished the temple
Solomon finished the temple Nehemiah 8:4-6
Nehemiah 8:4-6 Temple veil torn picture
Temple veil torn picture 7 woders of the world
7 woders of the world Jesus enters the temple
Jesus enters the temple Motivo lirico
Motivo lirico Old testament jewish temple layout
Old testament jewish temple layout What is om
What is om Poema con actitud carminica
Poema con actitud carminica Ezekiel temple
Ezekiel temple Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple Escuela industrial ernesto bertelsen temple
Escuela industrial ernesto bertelsen temple Solomon's temple location
Solomon's temple location Martempering
Martempering Temple of the white tiger
Temple of the white tiger Solomon finished the temple
Solomon finished the temple Fifty thousand drachmas
Fifty thousand drachmas Temple of bacchus facts
Temple of bacchus facts Rajarajeshvara temple, thanjavur, india, ca. 1010
Rajarajeshvara temple, thanjavur, india, ca. 1010 Maxwell thermodynamic relations
Maxwell thermodynamic relations Temple isss
Temple isss Isle of bali
Isle of bali Jesus clears the temple
Jesus clears the temple Temple breakout rooms
Temple breakout rooms Pintar sobre el oro bruñido relieves al temple
Pintar sobre el oro bruñido relieves al temple Cit upenn
Cit upenn Cis 2168
Cis 2168 Cis decalin newman projection
Cis decalin newman projection Unsaturated hydrocarbon examples
Unsaturated hydrocarbon examples Código de identificación de servicios (cis)
Código de identificación de servicios (cis) Cis548
Cis548 5 nada enharmonis
5 nada enharmonis Tuoli
Tuoli Are cis and trans diastereomers
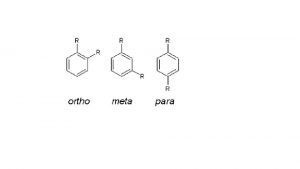
Are cis and trans diastereomers