Techniques for Highorder Adaptive Discontinuous Galerkin Discretizations in

Techniques for High-order Adaptive Discontinuous Galerkin Discretizations in Fluid Dynamics Dissertation Defense Li Wang Ph. D Candidate Department of Mechanical Engineering University of Wyoming Laramie, WY April 21, 2009

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

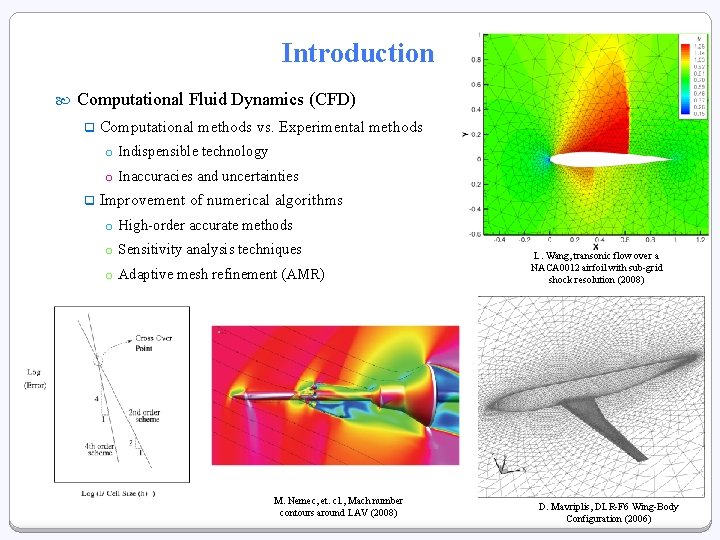
Introduction Computational Fluid Dynamics (CFD) q Computational methods vs. Experimental methods o Indispensible technology o Inaccuracies and uncertainties q Improvement of numerical algorithms o High-order accurate methods o Sensitivity analysis techniques o Adaptive mesh refinement (AMR) M. Nemec, et. cl. , Mach number contours around LAV (2008) L. Wang, transonic flow over a NACA 0012 airfoil with sub-grid shock resolution (2008) D. Mavriplis, DLR-F 6 Wing-Body Configuration (2006)

Introduction Why Discontinuous Galerkin (DG) Methods? q Finite difference methods o Simple geometries q Finite volume methods o Lower-order accurate discretizations q DG methods o Solution Expansion o Asymptotic accuracy properties: o Compact element-based stencils o Efficient performance in a parallel environment o Easy implementation of h-p adaptivity

Introduction High-order Time-integration Schemes q Explicit schemes (e. g. Explicit Runge-Kutta scheme) o Easy to solve o Restricted time-step sizes : o Run a lot of time steps q Implicit schemes o No restriction by CFL stability limit o Accuracy requirement o Accuracy o Computational cost Efficient Solution Strategies q q q Required for steady-state or time-implicit solvers p- or hp- nonlinear multigrid approach Element Jacobi smoothers

Introduction Sensitivity Analysis Techniques q Applications o Shape optimization o Output-based error estimation o Adaptive mesh refinement q Adjoint Methods o Linearization of the analysis problem + Transpose o Discrete adjoint method ü Reproduce exact sensitivities to the discrete system ü Deliver Linear systems o Simulation output : L(u), such as lift or drag o Error in simulation output: e(L) ~ (Adjoint solution) • (Residual of the Analysis Problem)

Objective Development of Efficient Solution Strategies for Steady or Unsteady Flows Development of Output-based Spatial Error Estimation and Mesh Adaptation Investigation of Time-Implicit Schemes Investigation of Output-based Temporal Error Estimation and Time-Step Adaptation

Model Problem Two-dimensional Compressible Euler Equations q Conservative Formulation

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

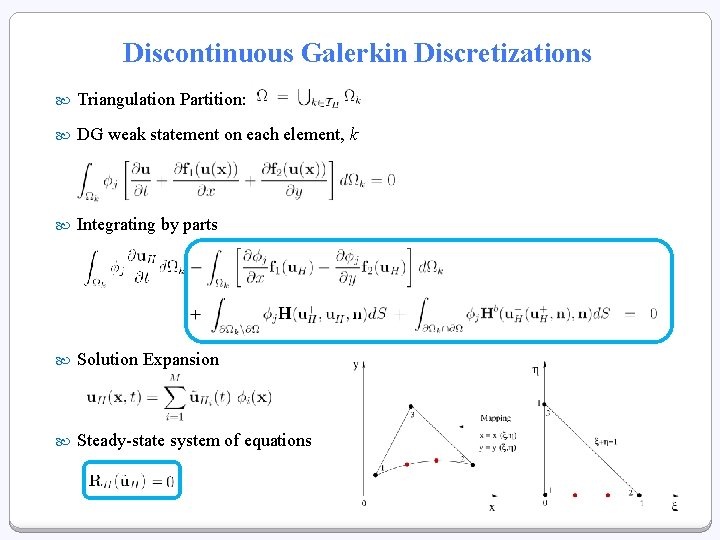
Discontinuous Galerkin Discretizations Triangulation Partition: DG weak statement on each element, k Integrating by parts Solution Expansion Steady-state system of equations

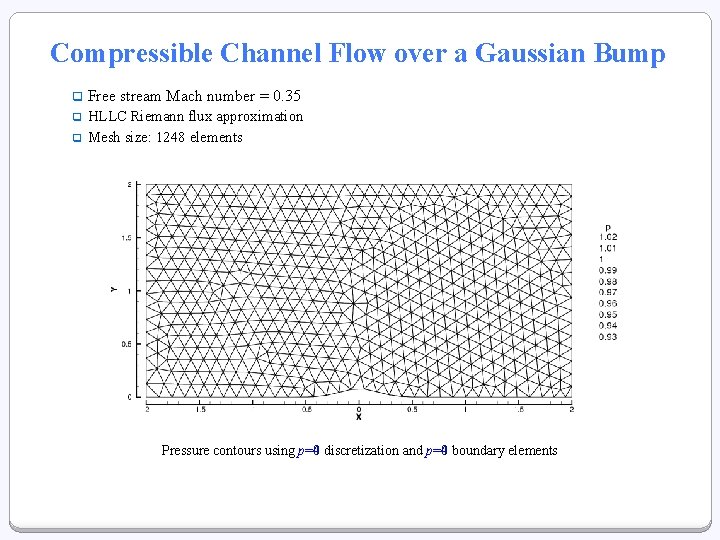
Compressible Channel Flow over a Gaussian Bump q Free stream Mach number = 0. 35 q HLLC Riemann flux approximation Mesh size: 1248 elements q Pressure contours using p=4 p=0 discretization and p=4 p=0 boundary elements

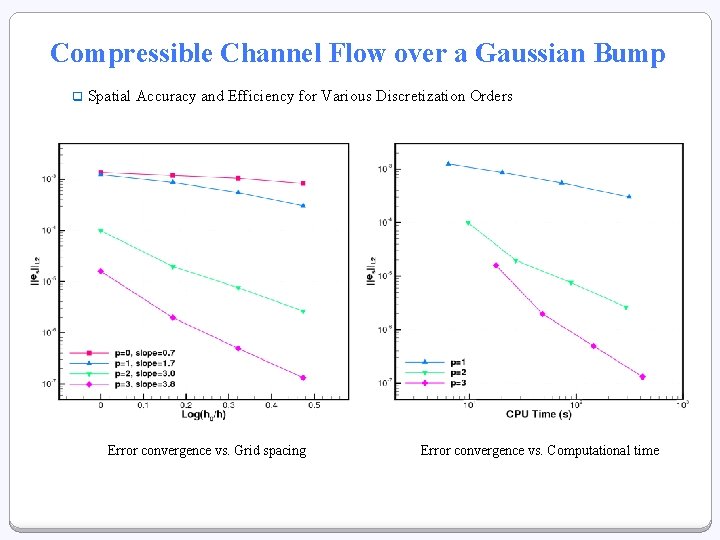
Compressible Channel Flow over a Gaussian Bump q Spatial Accuracy and Efficiency for Various Discretization Orders Error convergence vs. Grid spacing Error convergence vs. Computational time

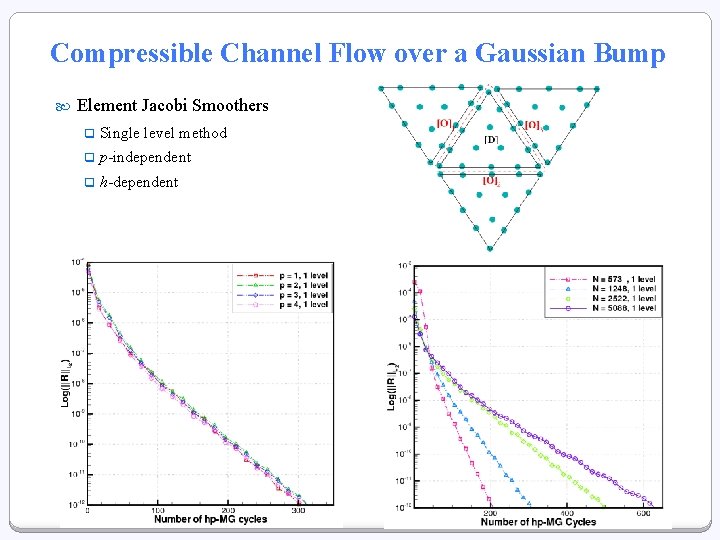
Compressible Channel Flow over a Gaussian Bump Element Jacobi Smoothers q Single level method q p-independent q h-dependent

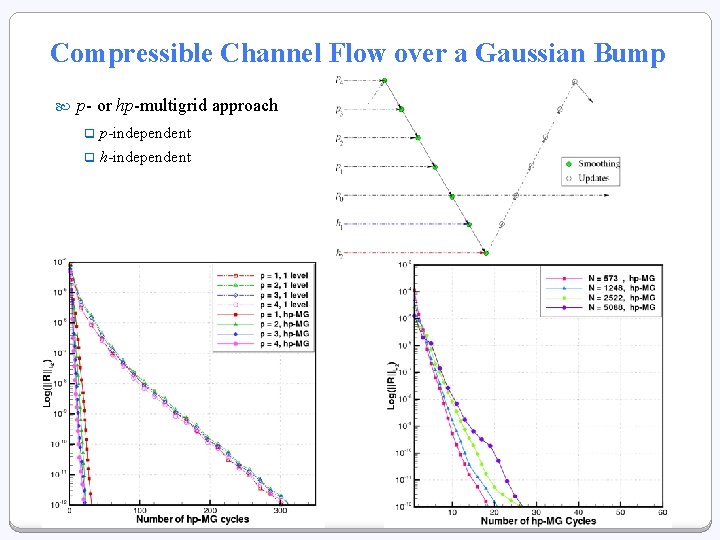
Compressible Channel Flow over a Gaussian Bump p- or hp-multigrid approach q p-independent q h-independent

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

Output-based Spatial Error Estimation Some key functional outputs in flow simulations q Lift, Drag, Integrated surface temperature, etc. q Surface integrals of the flow-field variables q Single objective functional, L Coarse affordable mesh, H q Coarse level flow solution, q Coarse level functional, Fine (Globally refined) mesh, h q Fine level flow solution, q Fine level functional, Goal: Find an approximation of without solving on the fine mesh

Output-based Spatial Error Estimation Goal: Find an approximation of Taylor series expansion without solving on the fine mesh

Output-based Spatial Error Estimation Discrete adjoint problem (H) q Transpose of Jacobian matrix q Delivers similar convergence rate as the flow solver Reconstruction of coarse level adjoint Approximated fine level functional q : Estimates functional error q : Indicates error distribution and drives mesh adaptation

Refinement Criteria is used to drive mesh adaptation Element-wise error indicator Criteria for refinement o Set an error tolerance, ETOL o Necessary refinement for an element if Flag elements required for refinement

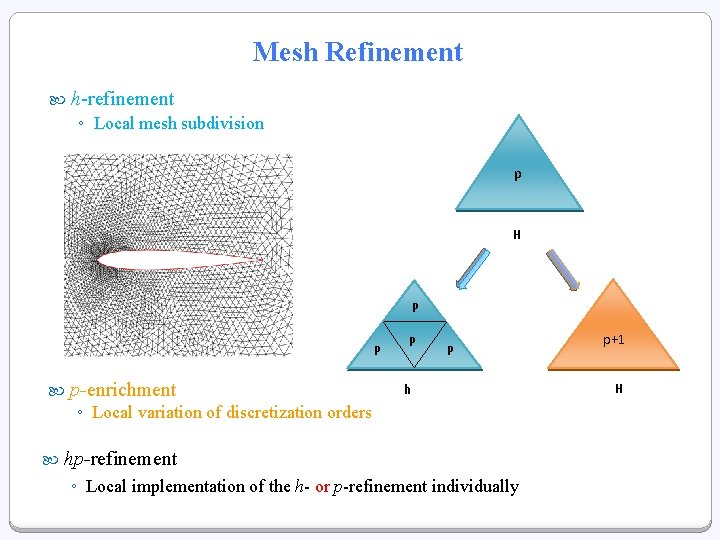
Mesh Refinement h-refinement ◦ Local mesh subdivision p H P P p-enrichment P P h ◦ Local variation of discretization orders hp-refinement ◦ Local implementation of the h- or p-refinement individually p+1 H

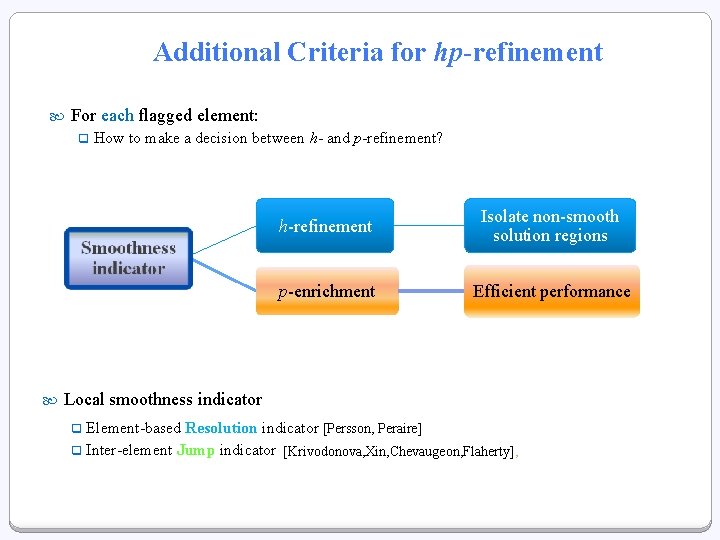
Additional Criteria for hp-refinement For each flagged element: q How to make a decision between h- and p-refinement? h-refinement Isolate non-smooth solution regions p-enrichment Efficient performance Criteria? ? Local smoothness indicator q q Element-based Resolution indicator [Persson, Peraire] Inter-element Jump indicator [Krivodonova, Xin, Chevaugeon, Flaherty],

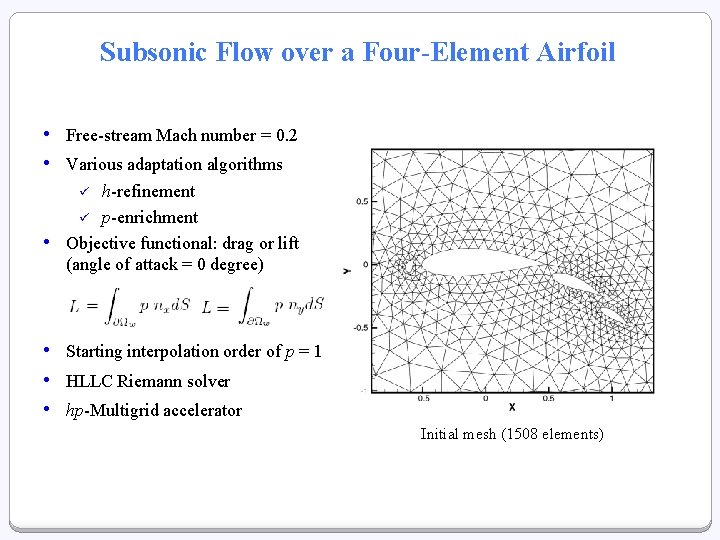
Subsonic Flow over a Four-Element Airfoil • Free-stream Mach number = 0. 2 • Various adaptation algorithms h-refinement ü p-enrichment Objective functional: drag or lift (angle of attack = 0 degree) ü • • Starting interpolation order of p = 1 • HLLC Riemann solver • hp-Multigrid accelerator Initial mesh (1508 elements)

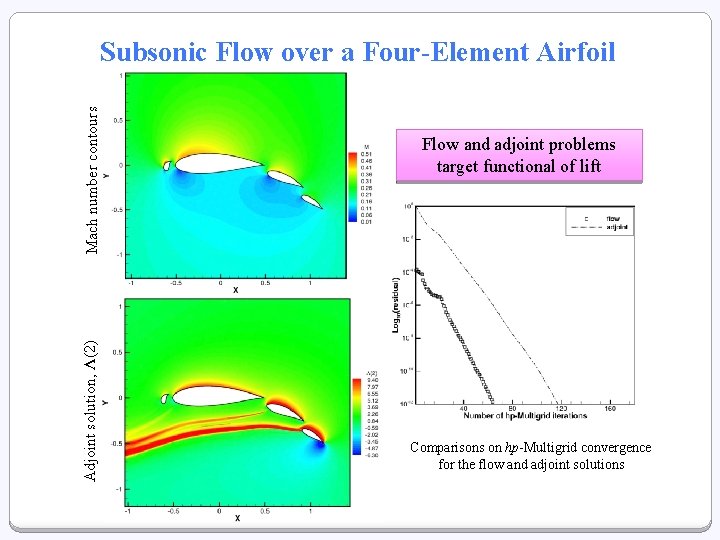
Adjoint solution, Λ(2) Mach number contours Subsonic Flow over a Four-Element Airfoil Flow and adjoint problems target functional of lift Comparisons on hp-Multigrid convergence for the flow and adjoint solutions

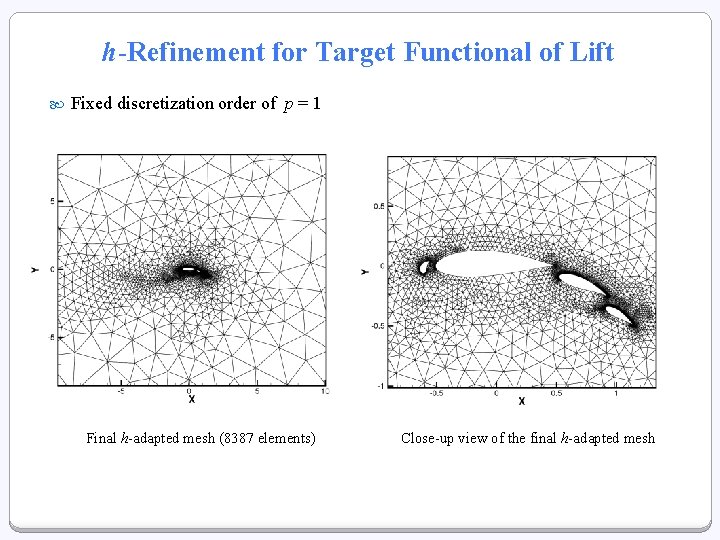
h-Refinement for Target Functional of Lift Fixed discretization order of p = 1 Final h-adapted mesh (8387 elements) Close-up view of the final h-adapted mesh

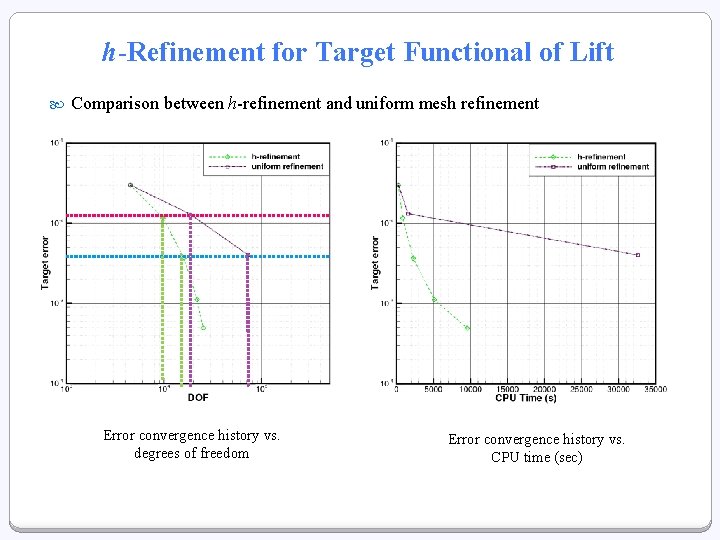
h-Refinement for Target Functional of Lift Comparison between h-refinement and uniform mesh refinement Error convergence history vs. degrees of freedom Error convergence history vs. CPU time (sec)

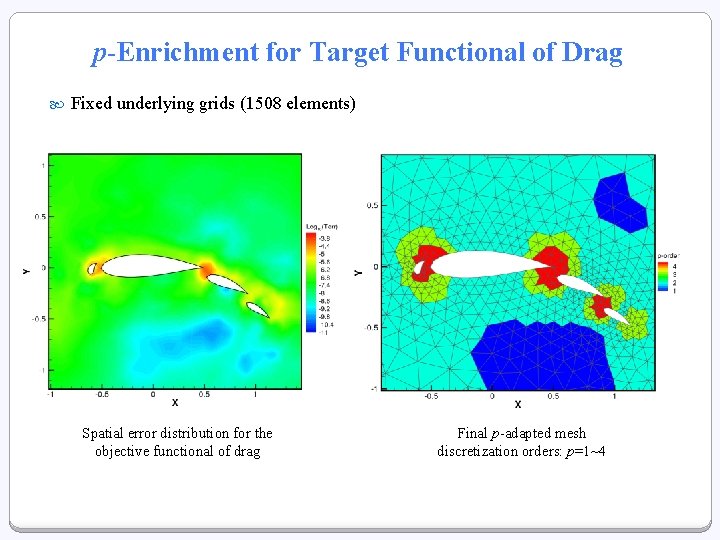
p-Enrichment for Target Functional of Drag Fixed underlying grids (1508 elements) Spatial error distribution for the objective functional of drag Final p-adapted mesh discretization orders: p=1~4

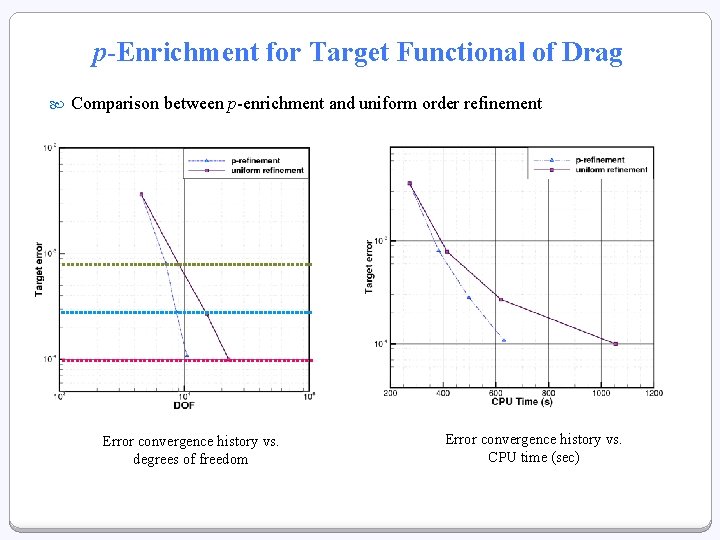
p-Enrichment for Target Functional of Drag Comparison between p-enrichment and uniform order refinement Error convergence history vs. degrees of freedom Error convergence history vs. CPU time (sec)

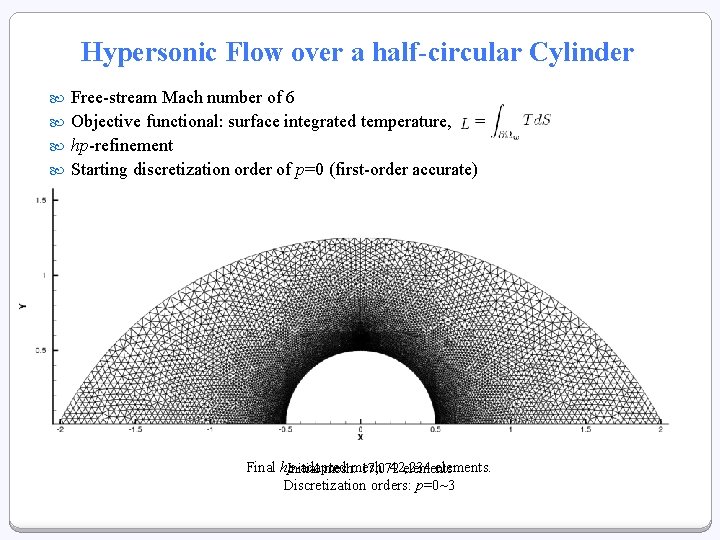
Hypersonic Flow over a half-circular Cylinder Free-stream Mach number of 6 Objective functional: surface integrated temperature, hp-refinement Starting discretization order of p=0 (first-order accurate) hp-adapted meshes Final hp-adapted 42, 234 elements. Initial mesh: 17, 072 elements Discretization orders: p=0~3

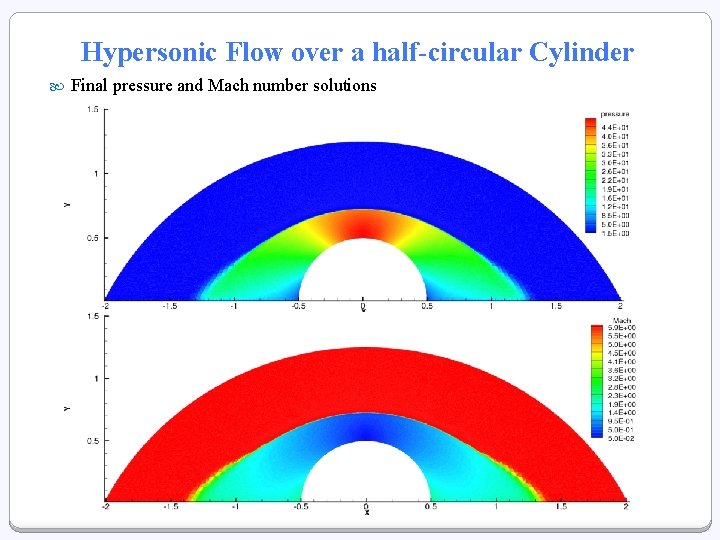
Hypersonic Flow over a half-circular Cylinder Final pressure and Mach number solutions

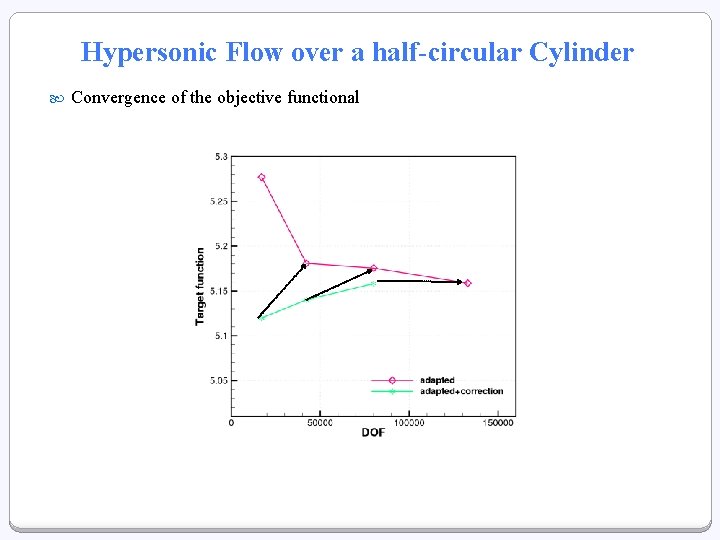
Hypersonic Flow over a half-circular Cylinder Convergence of the objective functional

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

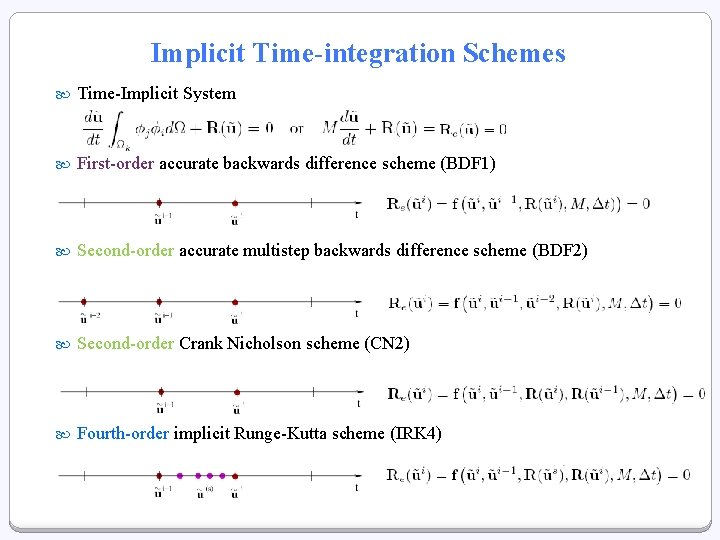
Implicit Time-integration Schemes Time-Implicit System First-order accurate backwards difference scheme (BDF 1) Second-order accurate multistep backwards difference scheme (BDF 2) Second-order Crank Nicholson scheme (CN 2) Fourth-order implicit Runge-Kutta scheme (IRK 4)

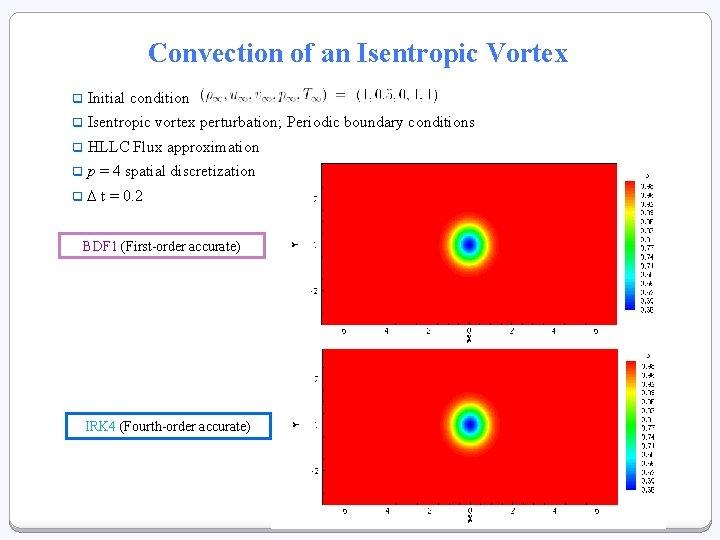
Convection of an Isentropic Vortex q Initial condition q Isentropic vortex perturbation; Periodic boundary conditions q HLLC Flux approximation q p = 4 spatial discretization q ∆ t = 0. 2 BDF 1 (First-order accurate) IRK 4 (Fourth-order accurate)

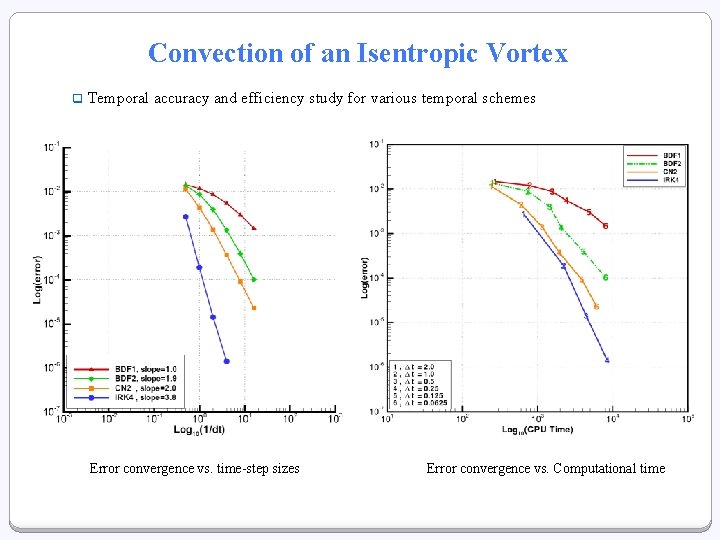
Convection of an Isentropic Vortex q Temporal accuracy and efficiency study for various temporal schemes Error convergence vs. time-step sizes Error convergence vs. Computational time

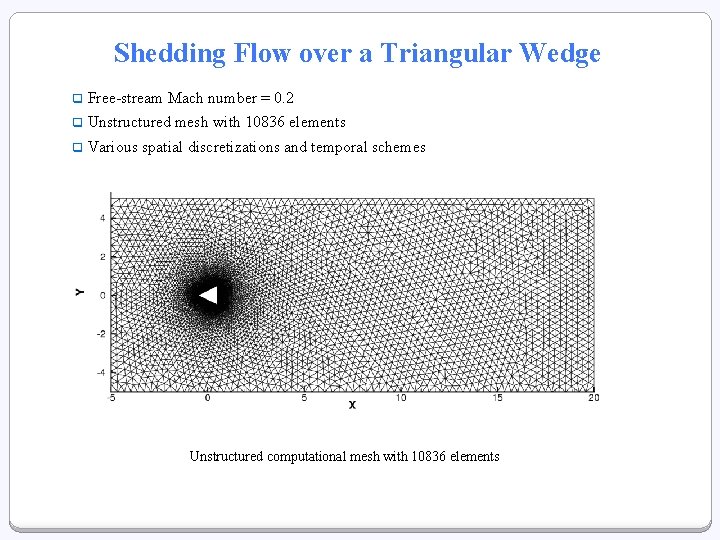
Shedding Flow over a Triangular Wedge q Free-stream Mach number = 0. 2 q Unstructured mesh with 10836 elements q Various spatial discretizations and temporal schemes Unstructured computational mesh with 10836 elements

Shedding Flow over a Triangular Wedge q Free-stream Mach number = 0. 2 q Unstructured mesh with 10836 elements q Various spatial discretizations and temporal schemes Density solution using p = 1 discretization and BDF 2 scheme

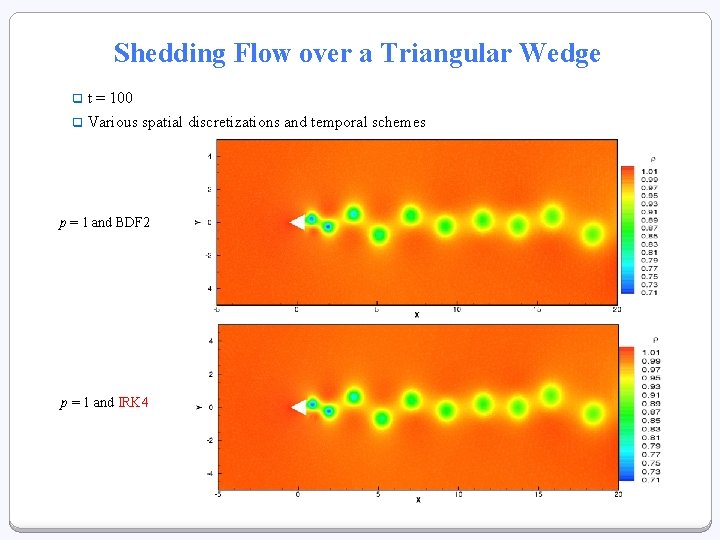
Shedding Flow over a Triangular Wedge q t = 100 q Various spatial discretizations and temporal schemes p = 1 and BDF 2 p = 1 and IRK 4

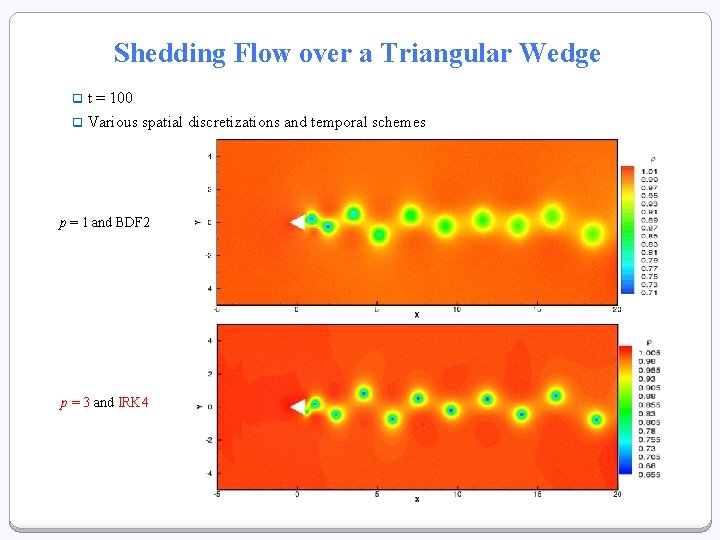
Shedding Flow over a Triangular Wedge q t = 100 q Various spatial discretizations and temporal schemes p = 1 and BDF 2 p = 3 and IRK 4

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

Output-based Temporal Error Estimation Same methodology can be applied in time q Global temporal error estimation and time-step adaptation q Implementation to BDF 1 and IRK 4 schemes q Time-integrated objective functional: q Unsteady Flow solution q Unsteady adjoint solution o Linearization of the unsteady flow equations o Transpose operation results in a backward time-integration Forward time-integration Current Backward time-integration

Output-based Temporal Error Estimation Two successively refined time-resolution levels q q H: coarse level functional h: fine level functional Approximation of fine level functional Localized functional error (for each time step i) BDF 1: IRK 4: Local time-step subdivision if

Shedding Flow over a Triangular Wedge Implementation for BDF 1 scheme ( p = 2) Validation of adjoint-based error correction Objective function: Drag at t = 5 q Error prediction for two time-resolution levels Refined timeresolution levels Computed functional error (Reconstructed adjoint) • (Unsteady residual)

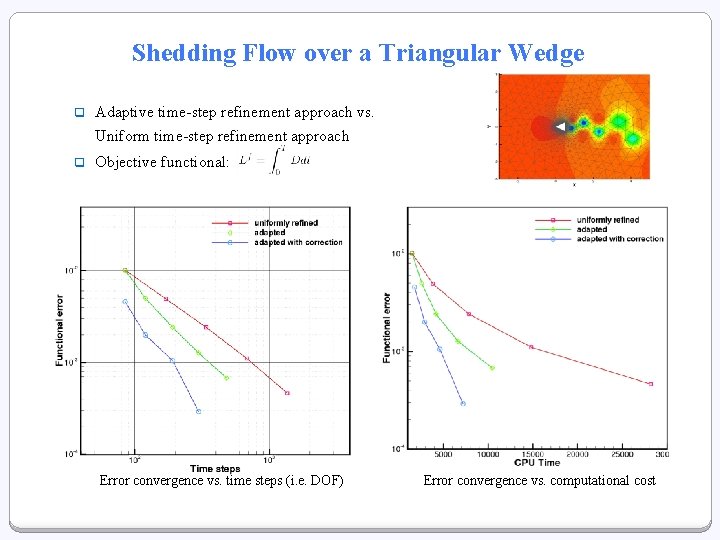
Shedding Flow over a Triangular Wedge q Adaptive time-step refinement approach vs. Uniform time-step refinement approach q Objective functional: Error convergence vs. time steps (i. e. DOF) Error convergence vs. computational cost

Outline Introduction Objective Steady Flow Problems q High-order Steady-State Discontinuous Galerkin Discretizations q Output-Based Spatial Error Estimation and Mesh Adaptation Unsteady Flow Problems q High-order Implicit Temporal Discretizations q Output-Based Temporal Error Estimation and Time-step Adaptation Conclusions and Future Work

Conclusions High-order DG and Implicit-Time Methods q Optimal error convergence rates are attained for the DG discretizations q Perform more efficiently than lower-order methods q Both h- and p-independent convergence rates q An attempt to balance spatial and temporal error q Perform more efficiently than lower-order implicit temporal schemes q h-independent convergence rates and slightly dependent on time-step sizes Discrete Adjoint based Sensitivity Analysis q Formulation of discrete adjoint sensitivity for DG discretizations q Accurate error estimate in a simulation output q Superior efficiency over uniform mesh or order refinement approach q hp-adaptation shows good capturing of strong shocks without limiters q Extension to temporal schemes q Superior efficiency over uniform time-step refinement approach

Future Work Dynamic Mesh Motion Problems q Discretely conservative high-order DG q Both high-order temporal and spatial accuracy q Unsteady shape optimization problems with mesh motion Robustness of the hp-adaptive refinement strategy q Incorporation of a shock limiter q Investigation of smoothness indicators Combination of spatial and temporal error estimation q Quantification of dominated error source q More effective adaptation strategies Extension to other sets of equations q Compressible Navier-Stokes equations (IP method) q Three-dimensional problems