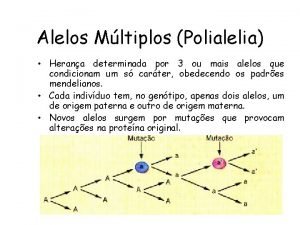
Quando necessrio escolher apenas uma ideologia utilizase uma

Quando é necessário escolher apenas uma ideologia, utiliza-se uma escolha, por meio de sufrágios ou votos que se designa por ELEIÇÃO O processo eleitoral tem dois momentos: · a votação · a contagem de votos. Como funciona a contagem? Será um processo justo? Será que existem eleitores com mais poder de voto do que outros?

1. VOTOS DE PREFERÊNCIAS. TABELAS DE PREFERÊNCIAS. Os votos de preferência são votos em que o eleitor escolhe, por ordem de preferência, os candidatos. Uma forma lógica de organizar os votos é agrupar os que são idênticos, e elaborar uma tabela de preferências. Uma vez que a Universidade de Coimbra encontra-se sem reitor, suponhamos que temos quatro candidatos para ocupar o lugar vago. São eles o Dr. António , o Dr. Bernardo, a Dra. Carolina e a Dra. Daniela. Há 37 pessoas com direito a voto nesta eleição, que constituem a população eleitora. Façamos a seguinte correspondência: A António B Bernardo C Carolina D Daniela.

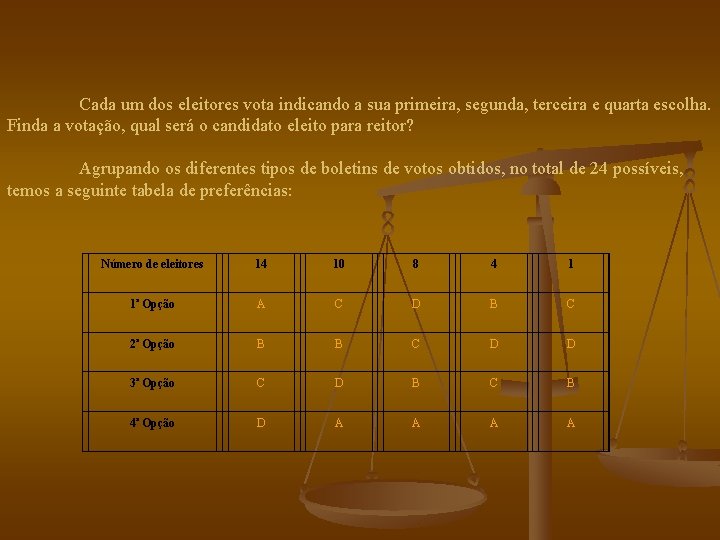
Cada um dos eleitores vota indicando a sua primeira, segunda, terceira e quarta escolha. Finda a votação, qual será o candidato eleito para reitor? Agrupando os diferentes tipos de boletins de votos obtidos, no total de 24 possíveis, temos a seguinte tabela de preferências: Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A

TRANSITIVIDADE E ELIMINAÇÃO DE CANDIDATOS Há dois factos a ter em conta quando se usam os votos de preferências: transitividade da preferência individual escolhas relativas de um eleitor não são afectadas pela eliminação de um ou mais candidatos. Exemplificação: VOTO 1º - C 2º - B 3º - D 4º - A 1º - C 2º - D 3º - A

2. MÉTODO DA PLURALIDADE O candidato que obtiver o maior número de colocações em primeiro lugar será o eleito. Aplicando este método ao nosso exemplo inicial, temos que: A obtém 14 votos para 1º lugar; B obtém 4 votos para 1º lugar; C obtém 11 votos para 1º lugar; D obtém 8 votos para 1º lugar. Neste caso, o resultado da escolha é óbvio – o eleito é o candidato A (o Dr. António). Características: Simplicidade Aplicação do princípio da regra da maioria A maioria implica a pluralidade e o recíproco não se verifica. Tal facto conduz-nos até ao critério da maioria.

CRITÉRIO DA MAIORIA: Se uma escolha obtiver a maioria das colocações em primeiro lugar numa eleição, então essa escolha deverá ser a eleita. CRITÉRIO DE CONDORCET: Se houver uma escolha, em que comparativamente com todas as outras, seja a preferida pelos eleitores, então essa escolha deverá ser a eleita.

Falhas do método da pluralidade: não considera outras preferências além da primeira mau resultado eleitoral não verifica o critério de Condorcet existência de votos que não revelam a verdadeira preferência dos eleitores Marie Jean Antoine Caritat – Marquis de Condorcet (1743 – 1794) Dedicou-se às Ciências Sociais É possível encontrar exemplos de eleições em que um candidato ganha em comparação com outros, mas ainda assim, pelo método da pluralidade, esse candidato perde a eleição. A esse candidato que ganha em comparação com os outros designa-se por CANDIDATO CONDORCET.

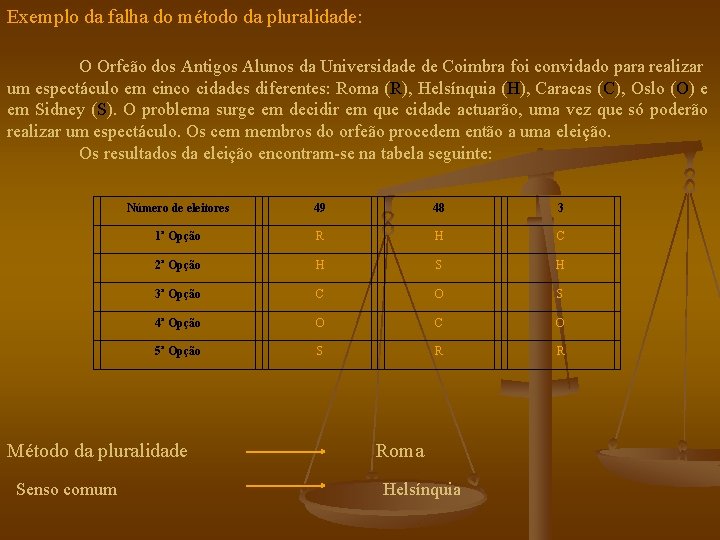
Exemplo da falha do método da pluralidade: O Orfeão dos Antigos Alunos da Universidade de Coimbra foi convidado para realizar um espectáculo em cinco cidades diferentes: Roma (R), Helsínquia (H), Caracas (C), Oslo (O) e em Sidney (S). O problema surge em decidir em que cidade actuarão, uma vez que só poderão realizar um espectáculo. Os cem membros do orfeão procedem então a uma eleição. Os resultados da eleição encontram-se na tabela seguinte: Número de eleitores 49 48 3 1ª Opção R H C 2ª Opção H S H 3ª Opção C O S 4ª Opção O C O 5ª Opção S R R Método da pluralidade Roma Senso comum Helsínquia

3 - MÉTODO DE CONTAGEM DE BORDA Neste método, a cada lugar nos votos de preferências é atribuída uma pontuação. Numa eleição com n candidatos atribui-se : um ponto último lugar dois pontos penúltimo lugar. . . n pontos primeiro lugar. Somam-se os pontos que foram atribuídos a cada candidato, e o que obtiver o maior número de pontos é o vencedor da eleição. Características do método: considera toda a informação que provem dos votos de preferência; é bastante usado quando existe um número significativo de candidatos.

Usando este método vejamos qual é o candidato eleito, no exemplo. A tabela seguinte mostra os pontos obtidos por cada candidato: Número de eleitores 14 10 8 4 1 1ª Opção: 4 pts A: 56 pts C: 40 pts D: 32 pts B: 16 pts C: 4 pts 2ª Opção: 3 pts B: 42 pts B: 30 pts C: 24 pts D: 12 pts D: 3 pts 3ª Opção: 2 pts C: 28 pts D: 20 pts B: 16 pts C: 8 pts B: 2 pts D: 14 pts A: 10 pts A: 8 pts A: 4 pts A: 1 pt 4ª Opção: 1 pt Agora somemos os pontos: A obtém: 4 * 14 + 1 * 10 + 1 * 8 + 1 * 4 + 1 * 1 = 79 pontos; B obtém: 3 * 14 + 3 * 10 + 2 * 8 + 4 * 4 + 2 * 1 = 106 pontos; C obtém: 2 * 14 + 4 * 10 + 3 * 8 + 2 * 4 + 4 * 1 =104 pontos; D obtém: 1 * 14 + 2 * 10 + 4 * 8 + 3 * 4 + 3 * 1 = 81 pontos; portanto o vencedor é o candidato B (Dr. Bernardo).

Falhas do método: não satisfaz o critério da maioria não verifica o critério de Condorcet Para ilustrar a falha deste método vejamos o seguinte exemplo Suponhamos que temos de eleger um representante do curso de Matemática, sendo os candidatos possíveis: o Joaquim, o Rodrigues, a Carlota e a Lucília. Façamos a seguinte correspondência: J Dr. Joaquim R Dr. Rodrigues C Dra. Carlota L Dra. Lucília. Após a entrevista dos quatro candidatos os onze membros da direcção votaram nos candidatos e decidiram usar este método para escolher este vencedor.

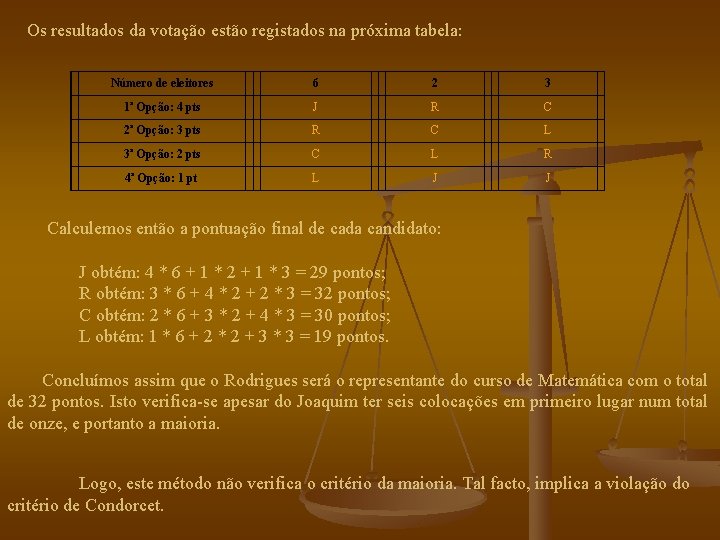
Os resultados da votação estão registados na próxima tabela: Número de eleitores 6 2 3 1ª Opção: 4 pts J R C 2ª Opção: 3 pts R C L 3ª Opção: 2 pts C L R 4ª Opção: 1 pt L J J Calculemos então a pontuação final de cada candidato: J obtém: 4 * 6 + 1 * 2 + 1 * 3 = 29 pontos; R obtém: 3 * 6 + 4 * 2 + 2 * 3 = 32 pontos; C obtém: 2 * 6 + 3 * 2 + 4 * 3 = 30 pontos; L obtém: 1 * 6 + 2 * 2 + 3 * 3 = 19 pontos. Concluímos assim que o Rodrigues será o representante do curso de Matemática com o total de 32 pontos. Isto verifica-se apesar do Joaquim ter seis colocações em primeiro lugar num total de onze, e portanto a maioria. Logo, este método não verifica o critério da maioria. Tal facto, implica a violação do critério de Condorcet.

4 -MÉTODO DA PLURALIDADE COM ELIMINAÇÃO Este método é uma versão do princípio da sobrevivência dos mais aptos. A ideia básica é a contínua eliminação dos candidatos menos aptos, um a um, até que surja um vencedor. O critério para a aptidão é o número de colocações em primeiro lugar que se obtém. Características do método: é utilizado em eleições com poucos candidatos ( normalmente 3 ou 4 e raramente mais do que 6).

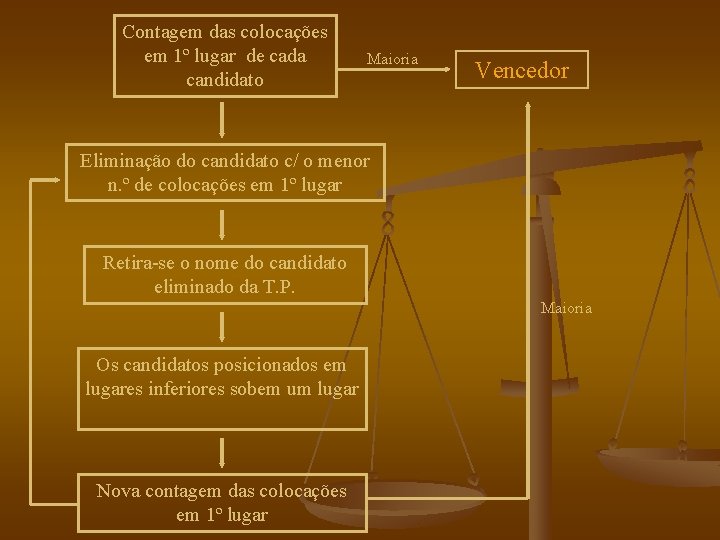
Contagem das colocações em 1º lugar de cada candidato Maioria Vencedor Eliminação do candidato c/ o menor n. º de colocações em 1º lugar Retira-se o nome do candidato eliminado da T. P. Maioria Os candidatos posicionados em lugares inferiores sobem um lugar Nova contagem das colocações em 1º lugar

Apliquemos este método à eleição do reitor da Universidade de Coimbra. Relembremos a tabela 1: Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A PASSO 1: Candidato A B C D Nº de votos da 1ª Opção 14 4 11 8 Como o candidato B é o que possui o menor número de votos na 1ª opção, ele é eliminado.

PASSO 2: Devido à eliminação de B, obtemos uma nova tabela: Número de eleitores 14 10 8 4 1 1ª Opção A C D D C 2ª Opção C D C C D 3ª Opção D A A Procedendo-se a uma recontagem dos votos, surge a seguinte tabela: Candidato A B C D Nº de votos para 1ª Opção 14 - 11 12 Neste passo, o candidato C é o eliminado pois possui o menor número de votos. PASSO 3: Os onze votos pertencentes ao candidato C no passo 2 deslocar-se-ão para o candidato D, como se verifica na seguinte tabela: Número de eleitores 14 10 8 4 1 1ª Opção A D D 2ª Opção D A A O candidato D obteve a maioria dos votos da primeira opção no passo 3, uma vez que é apenas necessário 19 votos para que haja uma maioria, verificando-se assim o critério da maioria.

CRITÉRIO DA MONOTONIA: Se uma escolha X for a vencedora de uma eleição e, numa reeleição, as únicas mudanças nos votos forem mudanças que favoreçam X, então a escolha X deverá permanecer como a eleita.

Falhas do método: não satisfaz o critério da monotonia não verifica o critério de Condorcet Vejamos o seguinte exemplo: No Departamento de Matemática da Universidade de Coimbra está prestes a realizar-se a eleição para o presidente do Núcleo de Estudantes de Matemática e Engenharia Geográfica (NEMATEG). Há três candidatos ao cargo que são a Ana (A), a Vera (V) e o Manuel (M). População eleitora- 29 membros Número de eleitores 7 8 10 4 1ª Opção A V M A 2ª Opção V M A M 3ª Opção M A V V Passo 1→ Ana obteve 11 votos, a Vera 8 e o Manuel 10 Vera é eliminada Passo 2 → 8 votos que pertenciam à Vera são transferidos para o Manuel é o presidente do NEMATEG (18 votos)

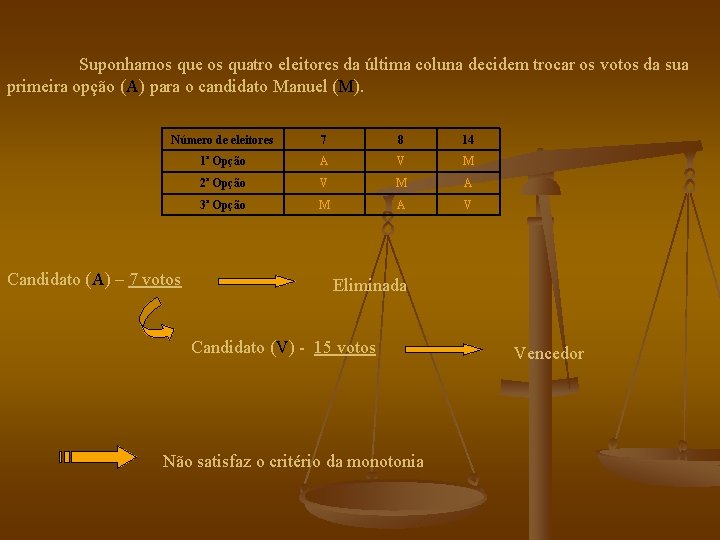
Suponhamos que os quatro eleitores da última coluna decidem trocar os votos da sua primeira opção (A) para o candidato Manuel (M). Número de eleitores 7 8 14 1ª Opção A V M 2ª Opção V M A 3ª Opção M A V Candidato (A) – 7 votos Eliminada Candidato (V) - 15 votos Não satisfaz o critério da monotonia Vencedor

5. MÉTODO DAS COMPARAÇÕES PAR A PAR Cada candidato é comparado com os restantes , sendo essas comparações feitas entre dois candidatos de cada vez. Quantas comparações são necessárias para encontrar um vencedor ? Depende do número de candidatos pois se existirem N candidatos temos as seguintes comparações: 1º candidato N-1 comparações 2º candidato N-2 comparações. . . Penúltimo candidato 1 comparação são precisas 1 + 2 + 3 + … + (N-2) + (N-1) = N (N-1)/2 comparações

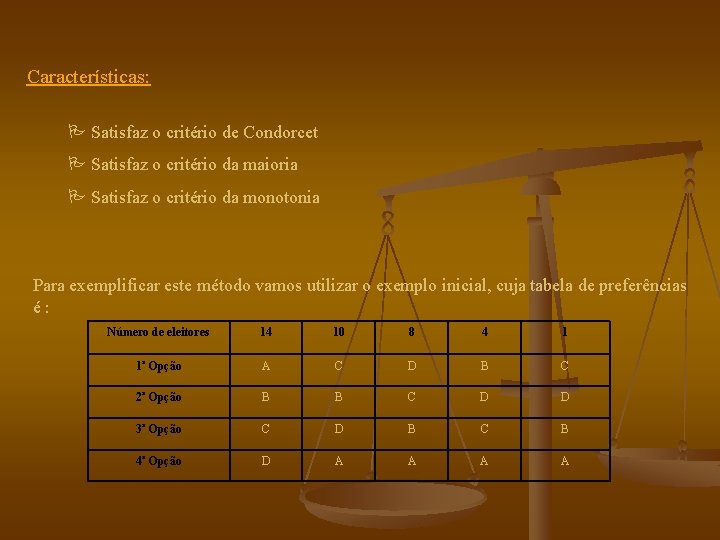
Características: Satisfaz o critério de Condorcet Satisfaz o critério da maioria Satisfaz o critério da monotonia Para exemplificar este método vamos utilizar o exemplo inicial, cuja tabela de preferências é : Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A

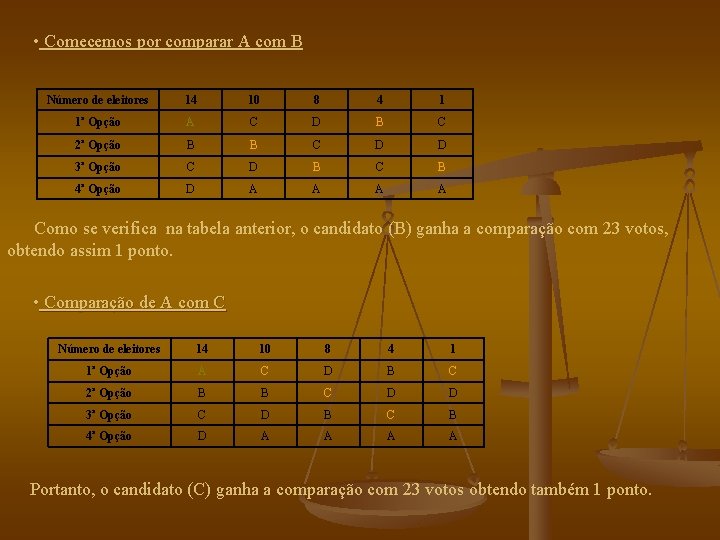
• Comecemos por comparar A com B Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A Como se verifica na tabela anterior, o candidato (B) ganha a comparação com 23 votos, obtendo assim 1 ponto. • Comparação de A com C Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A Portanto, o candidato (C) ganha a comparação com 23 votos obtendo também 1 ponto.

• Comparação entre os candidato A e D Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A Verificamos que o candidato D ganha a comparação com 23 votos, ficando com 1 ponto. • Comparação entre os candidatos B e C Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A O candidato C ganha a comparação com 19 votos contra 18 votos do candidato B

• Comparação entre os candidatos B e D Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A O candidato B obteve 1 ponto ao ganhar a comparação com D. • Comparação entre os candidatos C e D Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A O candidato C ganha a comparação com 25 votos, obtendo assim 1 ponto.

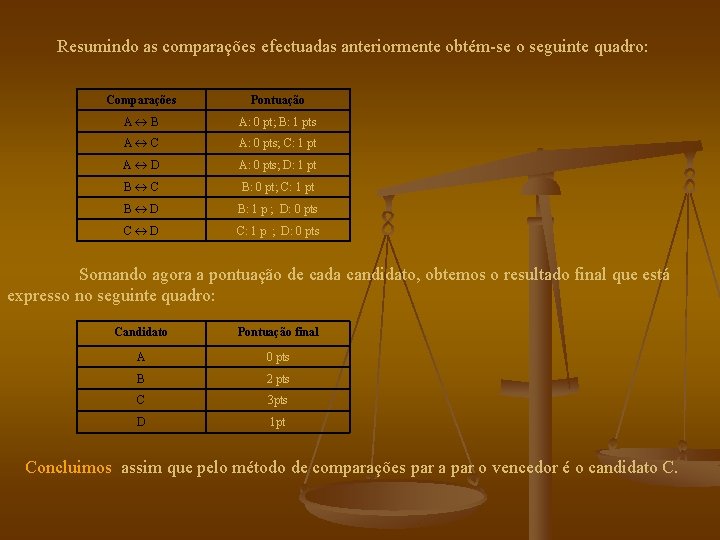
Resumindo as comparações efectuadas anteriormente obtém-se o seguinte quadro: Comparações Pontuação A B A: 0 pt; B: 1 pts A C A: 0 pts; C: 1 pt A D A: 0 pts; D: 1 pt B C B: 0 pt; C: 1 pt B D B: 1 p ; D: 0 pts C D C: 1 p ; D: 0 pts Somando agora a pontuação de cada candidato, obtemos o resultado final que está expresso no seguinte quadro: Candidato Pontuação final A 0 pts B 2 pts C 3 pts D 1 pt Concluimos assim que pelo método de comparações par a par o vencedor é o candidato C.

CRITÉRIO DE INDEPENDÊNCIA DAS ALTERNATIVAS IRRELEVANTES: Se a escolha X for a vencedora de uma eleição e uma (ou mais) das outras escolhas for removida e houver uma nova contagem dos votos, então X deverá continuar a ser a escolha eleita.

Falhas deste método: Pode produzir um resultado em que todos os candidatos são vencedores; Não satisfaz o critério de independência das alternativas irrelevantes. Para ilustrar estas duas falhas vamos apresentar dois exemplos: EXEMPLO 1: Os onze quartanistas do nosso curso vão realizar um jantar de curso, de modo a angariar algum dinheiro para participarem no cortejo da Queima das Fitas. É então necessário escolher o local do jantar entre os seguintes restaurantes: o Batina (B), a Liga (L) e o Democrática (D). A tabela de preferências é: Nº de Eleitores 4 2 5 1ª Opção B L D 2ª Opção L D B 3ª Opção D B L

Analisando a tabela anterior obtemos o seguinte quadro: Comparações Pontuação B L B: 1 pts ; L: 0 pts B D B: 0 pts ; D: 1 pts L D L: 1 pts ; D: 0 pts Chegamos assim, ao quadro da pontuação final: Candidato Pontuação final B 1 pt L 1 pt D 1 pt Notamos que existe uma situação de empate. E agora? Geralmente, não há uma regra pré -estabelecida para desempatar, mas na prática é importante estabelecer este tipo de regras.

EXEMPLO 2: Na Associação Académica de Coimbra existem várias secções desportivas. Na secção de Rugby, é necessário eleger um representante da equipa para receber o troféu de campeã nacional nesta modalidade. Há cinco voluntários: o Rafael (R), o João (J), o Miguel (M), o Luís (L) e o Gonçalo (G). A tabela seguinte mostra os votos de preferência dos eleitores: Nº de Eleitores 2 6 4 1 1 4 4 1ª Opção R L L M M J G 2ª Opção J R R L J R M 3ª Opção M M J R R G J 4ª Opção L J G J L M L 5ª Opção G G M G G L R Depois de efectuar as comparações par a par como foi feito no exemplo inicial temos o seguinte quadro: Candidato Pontuação final R 3 pts L 2 + ½ pts M 2 pts J 1 + ½ pts G 1 pt

O candidato eleito para ir receber o prémio em causa é o Rafael. O mais interessante neste exemplo, é que mesmo antes de ser anunciado o resultado da eleição, o Miguel comunica que não poderá ir receber o troféu caso seja o eleito. Uma vez que o Miguel não é a escolha principal, será que a sua desistência vai afectar o resultado? Suponhamos que o Miguel era eliminado no início da eleição, neste caso bastaria eliminá-lo do boletim de voto. Desta forma a tabela de preferências seria a seguinte: Nº de Eleitores 2 6 4 1 1 4 4 1ª Opção R L L L J J G 2ª Opção J R R R J 3ª Opção L J J J L G L 4ª Opção G G G L R

Finalmente depois de efectuadas as comparações necessárias temos o seguinte quadro: Candidato Pontuação final R 2 pts L 2 + ½ pts J 1 + ½ pts G 0 pts Logo, o vencedor seria o Luís. Por outras palavras, se a eleição fosse realizada com o conhecimento de que o Miguel não fazia parte do leque de candidatos, então o Luís seria o eleito e não o Rafael. Consequentemente o resultado original parece injusto para o Luís. Concluímos então que este método satisfaz todos os critérios enunciados até aqui excepto o critério de independência das alternativas irrelevantes.

2. 6. RANKINGS Muito frequentemente, é importante não só conhecer quem ganha as eleições mas também quem ficou em segundo lugar, terceiro lugar, etc. Para isto, temos dois métodos que são os seguintes: ➣ Métodos de ranking extensivos; ➣ Métodos recursivos de ranking ∲ MÉTODOS DE RANKING EXTENSIVOS ➸ Segundo o método da pluralidade : 1ª Posição: vencedor da eleição 2ª Posição: candidato com maior número de colocações em 1º lugar a seguir ao anterior . . . Última posição: candidato com menor número de colocações em 1º lugar

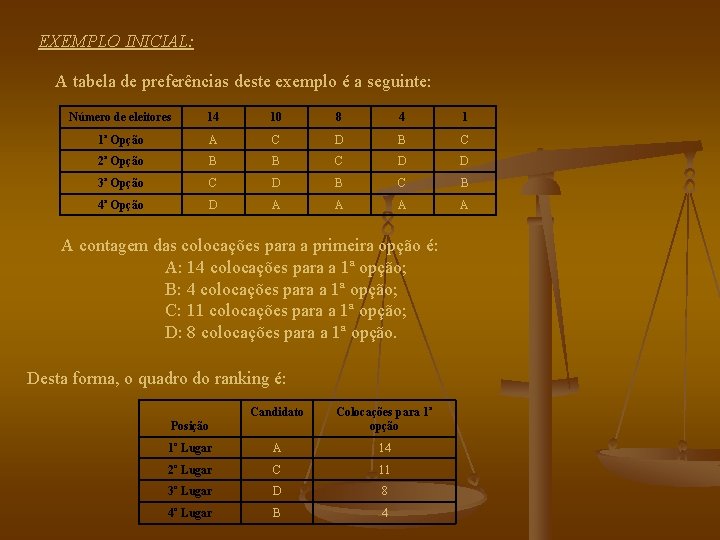
EXEMPLO INICIAL: A tabela de preferências deste exemplo é a seguinte: Número de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A A contagem das colocações para a primeira opção é: A: 14 colocações para a 1ª opção; B: 4 colocações para a 1ª opção; C: 11 colocações para a 1ª opção; D: 8 colocações para a 1ª opção. Desta forma, o quadro do ranking é: Candidato Colocações para 1ª opção 1º Lugar A 14 2º Lugar C 11 3º Lugar D 8 4º Lugar B 4 Posição

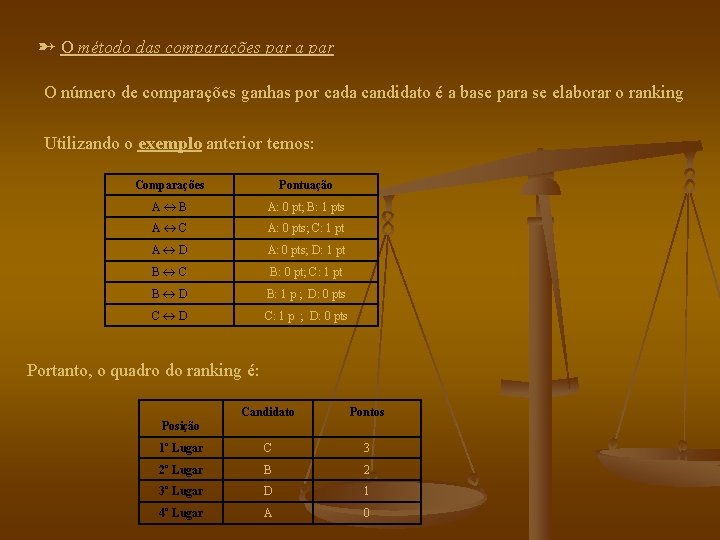
➸ O método das comparações par a par O número de comparações ganhas por cada candidato é a base para se elaborar o ranking Utilizando o exemplo anterior temos: Comparações Pontuação A B A: 0 pt; B: 1 pts A C A: 0 pts; C: 1 pt A D A: 0 pts; D: 1 pt B C B: 0 pt; C: 1 pt B D B: 1 p ; D: 0 pts C D C: 1 p ; D: 0 pts Portanto, o quadro do ranking é: Candidato Pontos 1º Lugar C 3 2º Lugar B 2 3º Lugar D 1 4º Lugar A 0 Posição

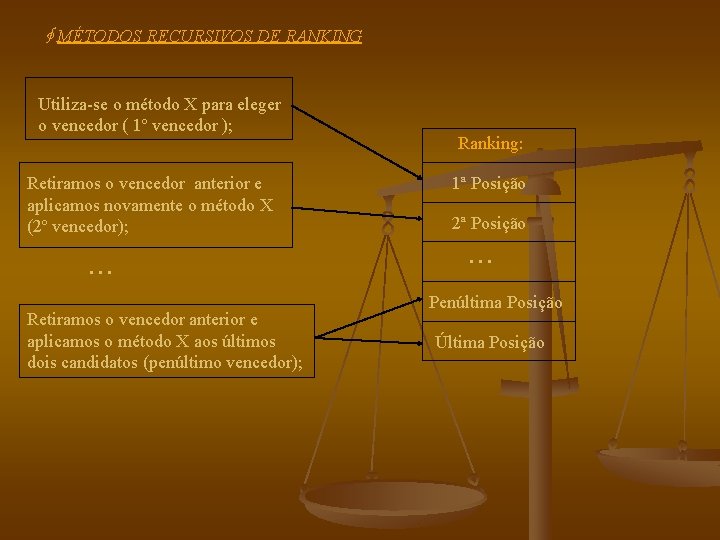
∲ MÉTODOS RECURSIVOS DE RANKING Utiliza-se o método X para eleger o vencedor ( 1º vencedor ); Retiramos o vencedor anterior e aplicamos novamente o método X (2º vencedor); . . . Retiramos o vencedor anterior e aplicamos o método X aos últimos dois candidatos (penúltimo vencedor); Ranking: 1ª Posição 2ª Posição. . . Penúltima Posição Última Posição

Para melhor ilustrar este processo vamos apresentar dois exemplos: ➸ Segundo o método da pluralidade recursivo : PASSO 1: O candidato eleito é o Dr. António com 14 colocações para a 1ª opção, logo é colocado no 1º lugar do ranking. PASSO 2: Removendo o candidato (A) da tabela original, obtemos uma nova tabela de preferências: Eleição original Após a remoção do candidato (A) Nº de eleitores 14 10 8 4 1 1ª Opção A C D B C 2ª Opção B B C D D 3ª Opção C D B C B 4ª Opção D A A Nº de eleitores 14 10 8 4 1 1ª Opção B C D B C 2ª Opção C B C D D 3ª Opção D D B C B Usando esta nova tabela concluímos que o candidato B é o vencedor, colocando-se em 2º lugar no ranking.

PASSO 3: Retirando desta vez o candidato (B), obtemos a seguinte tabela: Após a remoção dos candidatos (A) e (B) Nº de eleitores 14 10 8 4 1 1ª Opção C C D D C 2ª Opção D D C C D O candidato C é colocado na 3ª posição do ranking porque é o vencedor deste passo. Como só nos resta o candidato D, este fica na ultima posição do ranking. Finalmente o ranking recursivo deste método aparece no seguinte quadro: Posição Candidato 1º Lugar A 2º Lugar B 3º Lugar C 4º Lugar D

➸ Segundo o método das comparações par a par recursivo : Como vimos anteriormente, o resultado das comparações dos candidatos está no quadro seguinte: Pontuação final Candidato A 0 pts B 2 pts C 3 pts D 1 pt Portanto o vencedor é a Dra. Carolina (C), que colocamos no primeiro lugar do ranking. Depois de efectuar novas comparações temos o seguinte quadro: Comparações Pontuação A B A: 0 pts ; B: 1 pt A D A: 0 pts ; D: 1 pt B D B: 1 pt ; D: 0 pts

Concluímos assim o seguinte quadro: Candidato Pontuação Final A 0 pts B 2 pts D 1 pt Desta forma, o candidato (B) ganha, colocando-se em segundo lugar do ranking. Elimina-se o candidato (B) e temos então: Após remoção dos candidatos (B) e (C) Nº de eleitores 14 23 1ª Opção A D 2ª Opção D A Comparando A com D, o candidato D ganha a comparação e portanto este ocupará o terceiro lugar do ranking, e o candidato A ocupará o quarto lugar. Temos o seguinte quadro de ranking: Posição Candidato 1º Lugar C 2º Lugar B 3º Lugar D 4º Lugar A

Como foi visto, nenhum método anterior satisfaz os seguintes quatro critérios: CRITÉRIO DA MAIORIA: Se uma escolha obtiver a maioria das colocações em primeiro lugar numa eleição, então essa escolha deverá ser a eleita. CRITÉRIO DE CONDORCET: Se houver uma escolha, em que comparativamente com todas as outras, seja a preferida pelos eleitores, então essa escolha deverá ser a eleita. CRITÉRIO DA MONOTONIA: Se uma escolha X for a vencedora de uma eleição e, numa reeleição, as únicas mudanças nos votos forem mudanças que favoreçam X, então a escolha X deverá permanecer como a eleita. CRITÉRIO DE INDEPENDÊNCIA DAS ALTERNATIVAS IRRELEVANTES: Se a escolha X for a vencedora de uma eleição e uma (ou mais) das outras escolhas for removida e houver uma nova contagem dos votos, então X deverá continuar a ser a escolha eleita.

Kenneth Arrow (1921 - ) 1952 – Teorema da impossibilidade de Arrow 1972 – Prémio Nobel da Economia TEOREMA DA IMPOSSIBILIDADE DE ARROW: Um método democrático e justo para determinar o resultado de uma eleição é matematicamente impossível.

SISTEMA DE VOTO COM PESO: qualquer arranjo formal em que cada eleitor tem um número diferente de votos. VOTO PODER O melhor exemplo de um sistema de voto com peso: Ø Eleição do presidente dos Estados Unidos.

A principal vantagem de um sistema de voto com peso é de que: • Temos apenas duas hipóteses (aceitar ou recusar), • Não temos que nos preocupar com a escolha do método de voto a usar, pois todos eles seguem a: regra da maioria.

NOTAÇÕES: ü Jogador → Eleitor üMoção – apresentação de um assunto para ser discutido em assembleia; • Moção → Haver uma mudança;

ü Sistema de voto com peso : [C: P 1, . . . , PN] • C - cota isto é, o numero de votos necessários para que haja uma mudança; metade do total dos votos ≤ cota ≤ total dos votos • P 1, . . . , PN – o peso de voto de cada jogador, ordenados por ordem decrescente.

üChamam-se ditadores a todos os jogadores que tiverem peso de voto superior ou igual à cota. Exemplo: [11: 12, 5, 4] o primeiro jogador é ditador Numa situação em que há um ditador todos os outros jogadores ficam submetidos a ele, e estes jogadores chamam-se jogadores neutros.

Neste caso não há ditador: [12: 9, 5, 4, 2], e o jogador P 1, apesar de não ser ditador, tem o poder de obstruir, prevenindo qualquer mudança de posição dos restantes jogadores, isto é, que estes jogadores unam as forças e assim juntem mais votos que o primeiro jogador. Ao jogador P 1 é dado o poder de prevenir tais mudanças porque mesmo que os restantes jogadores votem juntos, estes não tem votos superiores à cota. Isto faz com eles não possam aceitar uma moção contra a vontade de P 1. O jogador que não é ditador mas que individualmente pode prevenir que os restantes jogadores juntos aceitem uma moção tem: Poder de Veto

1. INDICADOR DE PODER DE BANZHAF Em 1965 John Banzhaf introduziu uma interpretação matemática do poder para o sistema de voto com peso.

CONCEITOS IMPORTANTES: ØCOLIGAÇÃO: um grupo de jogadores que unem forças e juntos levarem à mudança. Esta designação também é válida para jogadores singulares. • COLIGAÇÃO VENCEDORA: são todas aquelas com votos suficientes para ganhar, as outras coligações são PERDEDORAS.

ØPESO DA COLIGAÇÃO: número total de votos controlado por uma coligação A coligação que contém todos os jogadores é sempre vencedora e chama-se grande coligação. Notação: coligação genérica de N eleitores é: {P 1, P 2, . . , PN}.

ØJOGADOR CRÍTICO: é o jogador que transforma uma coligação vencedora em perdedora ao abandonar a coligação. • Uma coligação vencedora pode ter mais do que um jogador crítico, e só ocasionalmente uma coligação não tem jogador crítico. • As coligações perdedoras nunca têm jogadores críticos. Este conceito é a base da definição para o indicador de poder de Banzhaf.

O poder do jogador é proporcional ao número de coligações para as quais ele é critico, isto é, quanto mais frequentemente um jogador é critico mais poder ele tem.

Para determinarmos o indicador de poder de Banzhaf de qualquer jogador num sistema de voto com peso genérico com N jogadores, seguimos os seguintes passos: ØPasso 1: fazer uma lista de todas as coligações possíveis, ØPasso 2: determinar quais são as coligações vencedoras, ØPasso 3: em cada coligação vencedora determinar quais são os jogadores críticos, ØPasso 4: contar o numero total de vezes que o jogador P, é critico – seja esse valor representado por B, ØPasso 5: contar o número total de vezes que todos os jogadores são críticos – seja esse valor representado por T

üO indicador de poder de Banzhaf é dado pela fracção: B/T. üA uma lista completa com os indicadores de poder de cada jogador, chamamos: distribuição de poder de Banzhaf. üÉ comum escrever os indicadores de poder em percentagem.

Para melhor percebermos os conceitos introduzidos anteriormente vamos analisar alguns exemplos: Sistema de voto com peso da forma: [101: 99, 98, 3]. À primeira vista somos conduzidos a pensar que os dois primeiros jogadores têm mais poder do que o terceiro. depois de analisarmos a situação verificamos que por mais estranho que nos pareça, os três jogadores tem o mesmo poder.

Coligações Peso da coligação Vence ou perde 1ª - {P 1} 99 Perde 2ª - {P 2} 98 Perde 3ª - {P 3} 3 Perde 4ª - {P 1, P 2} 197 Vence 5ª - {P 1, P 3} 102 Vence 6ª - {P 2, P 3} 101 Vence 7ª - {P 1, P 2, P 3} 200 Vence

üAs coligações 4, 5, 6, são vencedoras, mas basta que um jogador, o jogador crítico, abandone a coligação para que esta se torne numa coligação perdedora, üEm contrapartida a coligação 7 permanece vencedora mesmo que um jogador abandone a coligação, üAssim que cada jogador é duas vezes critico, concluímos que cada jogador tem um terço do poder: 2/6=1/3.

Numa empresa onde na direcção estão envolvidas três gerações da família Oliveira: üOliveira I → O 1 üOliveira II → O 2 üOliveira III → O 3 Cada membro tem um poder diferente nas decisões finais: O 1 → três votos, O 2 →dois votos, O 3 → um voto. São necessários quatro dos seis votos possíveis para que haja mudança, isto é, para que seja aceite a moção. O que dá origem a um sistema de voto com peso da forma: [4: 3, 2, 1].

Aplicando agora a cinco regras para o cálculo do indicador de poder de cada um dos jogadores, obtemos: 1º- Há sete coligações possíveis, {O 1} {O 2} {O 3} {O 1, O 2} {O 1, O 3} {O 2, O 3} {O 1, O 2, O 3}, 2º- Coligações vencedoras {O 1, O 2} {O 1, O 3} {O 1, O 2, O 3},

3º- Jogadores críticos O 1 e O 2 → coligação {O 1, O 2} O 1 e O 3 → coligação {O 1, O 3} Apenas O 1 → coligação {O 1, O 2, O 3}, 4º- O 1 é três vezes jogador crítico O 2 é uma vez jogador crítico O 3 é uma vez jogador critico, 5º- O número total de jogadores críticos é cinco.

O indicador de poder de Banzhaf de cada jogador é: O 1: 3/5 O 2: 1/5 O 3: 1/5 Sendo a distribuição de poder da forma: O 1 tem 60% do poder O 2 tem 20% do poder O 3 tem 20% do poder. Que a primeira geração tem mais poder, e que a segunda e terceira geração têm igual poder.

Quantas coligações existem para um dado número de jogadores? Identifiquemos as coligações com grupos. A cada subgrupo diferente, excluindo o subgrupo vazio, fazemos corresponder uma coligação. Existem tantas coligações quantos os subgrupos menos um, que é o subgrupo vazio.

A tabela seguinte mostra quantos subgrupos é possível formar com N elementos: Nº de jogadores Nº de subgrupos Nº de coligações 2 4=22 22 - 1=3 3 8=23 23 - 1=7 … … N 2 N – 1

Conselho de segurança das Nações Unidas Constituído por: 15 nações de voto → 5 permanentes → 10 não permanentes ü Para que uma moção seja aceite é necessário um voto a favor de cada um dos membros permanentes, mais votos adicionais a favor de pelo menos quatro dos dez membros não permanentes.

Coligações vencedoras Ø Contêm todos os membros permanentes mais pelo menos quatro dos membros não permanentes. Então existem: + + + = = 210 + 252 + 210 + 120 + 45 + 10 = 848 Coligações • Todos os membros permanentes são críticos nestas coligações.

• E os membros não permanentes são apenas críticos nas : Coligações vencedoras mínimas - são formadas pelos cinco membros permanentes e por exactamente quatro dos membros não permanentes. Então existem: = 84 Coligações

Número total de vezes que todos os jogadores são críticos: 5 * 848 + 10 * 84 = 5080. O indicador de poder de Banzhaf : ØMembros permanente é: 848/5080 = 0. 167 ou 16. 7% ØMembro não permanente é: 84/5080 = 0. 0165 ou 1. 65%

Os membros permanentes têm mais poder que os membros não permanentes

4. ÍNDICE DE PODER DE SHAPLEY - SHUBIK Neste método as coligações são formadas sequencialmente, isto é, é importante a ordem do eleitor na coligação (todas as coligações começam com um primeiro eleitor que pode ser seguido pelo segundo, depois o terceiro e assim sucessivamente). Palavra chave deste método: - Coligação Sequencial

IMPORTANTE: A questão da ordem de cada eleitor na coligação. Ilustre-se então a diferença com um simples exemplo. De acordo com a interpretação de Banzhaf -uma coligação com os eleitores {P 1, P 2, P 3} significa que P 1, P 2 e P 3 juntaram poder e votaram em conjunto, não interessando como formaram (a ordem) a coligação Segundo Shapley – Shubik, os mesmos três eleitores podem formar seis diferentes coligações sequenciais: <P 1, P 2, P 3> - significa que P 1 iniciou a coligação, em seguida juntou - se o eleitor P 2 e , por fim P 3.

Para um dado número de eleitores, N, quantas coligações sequenciais existem? Vamos ter n! coligações sequenciais possíveis. Em cada coligação sequencial existe um jogador que no momento em que este se junta á coligação, esta parte de perdedora a uma coligação vencedora. A este jogador daremos o nome de: PIVOT

Procedimento para encontrar o índice de poder de Shapley - Shubik de cada eleitor num sistema de voto com peso com N eleitores é o seguinte: 1º Passo – Fazer uma lista de todas as coligações sequenciais com os N eleitores, há N!. 2º Passo – Em cada coligação sequencial determinar o Pivot. ( Há um em cada. ) 3º Passo – contar o número de vezes que o eleitor P é Pivot. ( Designemo-lo por S ) O indicador de poder de Shapley – Shubik do eleitor P é dado por: S/N!

Exemplo: Vamos retomar o exemplo da empresa da família Oliveira considerada anteriormente. Tenhamos em conta que o sistema de votação que estamos a utilizar é 4 : 3, 2, 1 . Para a sua análise vamos então seguir os passos observados anteriormente.

Passo 1 < P 1, , P 2 , P 3 > < P 1, , P 3 , P 2 > < P 2, P 1 , P 3 > < P 2, , P 3 , P 1 > < P 3, P 1 , P 2 > < P 3, , P 2 , P 1 > Passo 2 Coligação sequencial Jogador pivotal < P 1, , P 2 , P 3 > P 2 < P 1, , P 3 , P 2 > P 3 < P 2, P 1 , P 3 > P 1 < P 2, , P 3 , P 1 > P 1 < P 3, P 1 , P 2 > P 1 < P 3, , P 2 , P 1 > P 1

Passo 3 P 1 é pivotal 4 vezes P 2 é pivotal 1 vez P 3 é pivotal 1 vez A distribuição de poder segundo o modelo de Shapley – Shubik é assim: P 1 4/6 = 66, (6)% P 2 1/6 = 16, (6)% P 3 1/6 = 16, (6)%

Conclusão: Podemos então concluir que a distribuição de poder dos dois métodos é diferente. Utilizando o modelo de Banzhaf P 1 : 60% ; P 2: 20%; P 3 : 20%. Utilizando o modelo de Shapley – Shubik P 1 : 66, (6)% P 2 : 16, (6)% P 3 : 16, (6)%

Interpretação: O Oliveira I tem ainda mais poder. Banzhaf Shapley -Shubik 60% 66, (6)% Em contrapartida o seu filho e o seu neto têm menos poder. Banzhaf Shapley -Shubik 20% 16, (6)% O Oliveira II continua com o mesmo poder que o filho.

Exemplo : Conselho de Segurança das Nações Unidas

No conselho de Segurança das Nações Unidas temos: 15 membros 5 membros permanentes 10 membros não permanentes De acordo com o método temos: 15! Coligações Sequenciais Quando é que um membro não permanente é pivotal? Nas coligações em que for precedido: - pelos 5 membros permanentes -por 3 não permanentes ( Podem ser escolhidos das possibilidades)

Estes 8 elementos podem ainda permutar entre si: temos assim mais 8! possibilidades Até agora temos 9 lugares preenchidos! Resta-nos ocupar os 6 restantes. Para estes existem 6! possibilidades. O índice de poder de cada membro é assim [ (9!8!)]/15! [(9!8!6!)/3!6!]/15! [(9!8!)/3!]/15!