Pseudo Gap Superconductivity and SuperconductorInsulator transition Mikhail Feigelman

Pseudo. Gap Superconductivity and Superconductor-Insulator transition Mikhail Feigel’man L. D. Landau Institute, Moscow In collaboration with: Vladimir Kravtsov Emilio Cuevas Lev Ioffe Marc Mezard ICTP Trieste University of Murcia Rutgers University Orsay University Short publications: Phys Rev Lett. 98, 027001 (2007) ar. Xiv: 0909. 2263

Plan of the talk 1. Motivation from experiments 2. BCS-like theory for critical eigenstates - transition temperature - local order parameter 3. Superconductivity with pseudogap - transition temperature v/s pseudogap 4. Quantum phase transition: Cayley tree 5. Conclusions

Superconductivity v/s Localization • Coulomb-induced suppression of Tc in uniform films “Fermionic mechanism” A. Finkelstein (1987) et al • Granular systems with Coulomb interaction K. Efetov (1980) M. P. A. Fisher et al (1990) “Bosonic mechanism” • Competition of Cooper pairing and localization (no Coulomb) Imry-Strongin, Ma-Lee, Kotliar-Kapitulnik, Bulaevsky-Sadovsky(mid-80’s) Ghosal, Randeria, Trivedi 1998 -2001 There will be no grains in this talk !

We consider amorphous systems with direct S-I transition

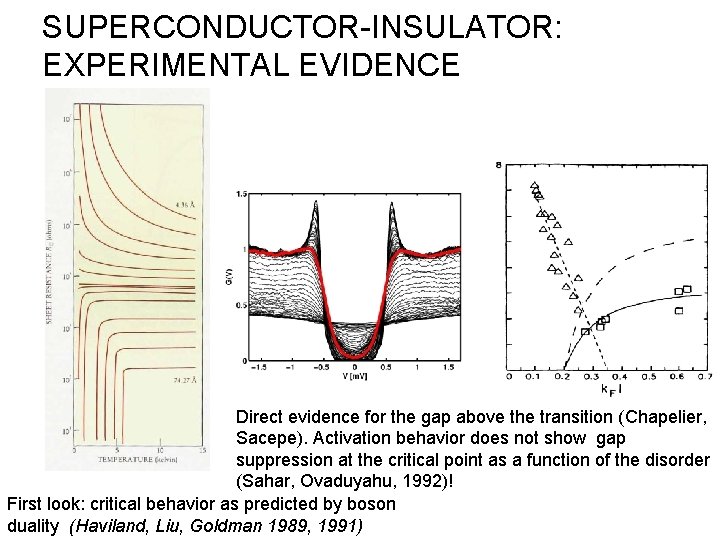
SUPERCONDUCTOR-INSULATOR: EXPERIMENTAL EVIDENCE Direct evidence for the gap above the transition (Chapelier, Sacepe). Activation behavior does not show gap suppression at the critical point as a function of the disorder (Sahar, Ovaduyahu, 1992)! First look: critical behavior as predicted by boson duality (Haviland, Liu, Goldman 1989, 1991)

Class of relevant materials • Amorphously disordered (no structural grains) • Low carrier density ( around 1021 cm-3 at low temp. ) Examples: In. Ox Nb. Nx thick films or bulk (+ B-doped Diamond? ) Ti. N thin films Be (ultra thin films) Special example: nanostructured Bi films (J. Valles et al)

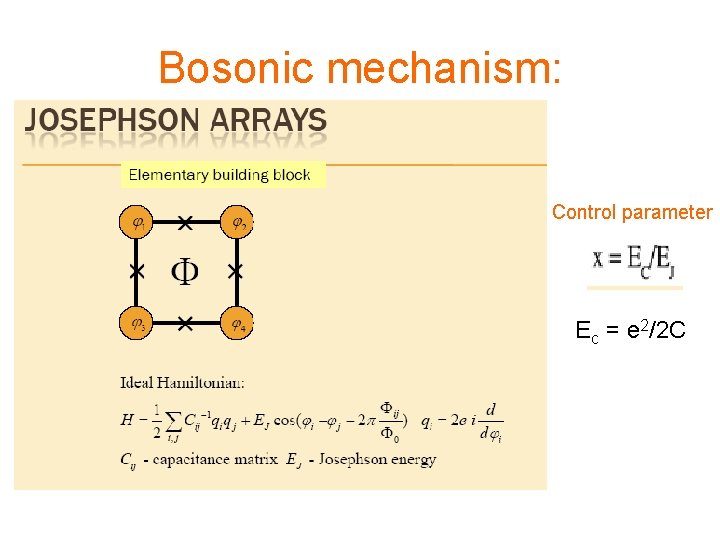
Bosonic mechanism: Control parameter Ec = e 2/2 C

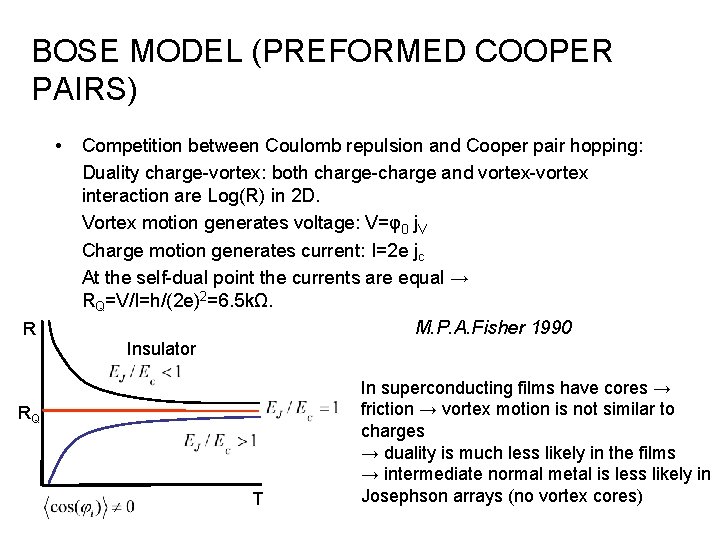
BOSE MODEL (PREFORMED COOPER PAIRS) • R Competition between Coulomb repulsion and Cooper pair hopping: Duality charge-vortex: both charge-charge and vortex-vortex interaction are Log(R) in 2 D. Vortex motion generates voltage: V=φ0 j. V Charge motion generates current: I=2 e jc At the self-dual point the currents are equal → RQ=V/I=h/(2 e)2=6. 5 kΩ. M. P. A. Fisher 1990 Insulator RQ T In superconducting films have cores → friction → vortex motion is not similar to charges → duality is much less likely in the films → intermediate normal metal is less likely in Josephson arrays (no vortex cores)

Duality approach to SIT in films Model of Josephson array (SC state) Duality transformation (approximate) Insulating state of Josepshon array ? ? ? Duality transformation (non-existing) Continous amorphous disordered film (SC state) ? ? ? ? Insulating state of disordered film

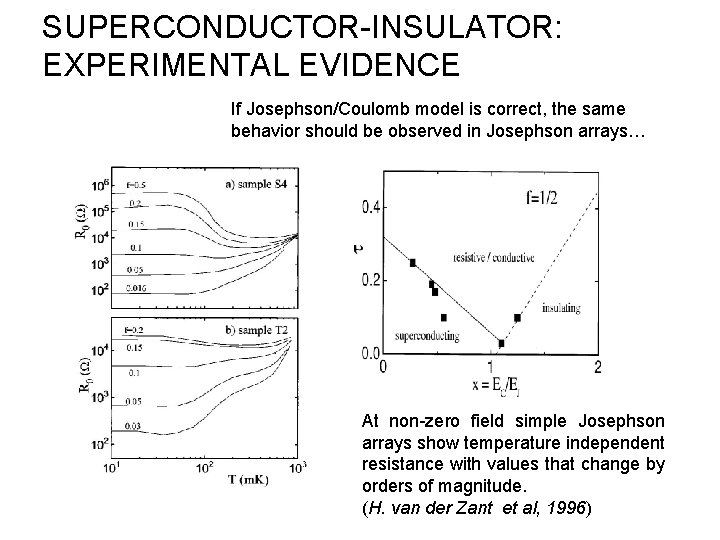
SUPERCONDUCTOR-INSULATOR: EXPERIMENTAL EVIDENCE If duality arguments are correct, the same behavior should be observed in Josephson arrays… First look: critical behavior as predicted by boson duality (Haviland, Liu, Goldman 1989, 1991) At zero field simple Josephson arrays show roughly the critical behavior. However, the critical R is not universal. (Zant and Mooji, 1996) and critical value of EJ/Ec differs.

SUPERCONDUCTOR-INSULATOR: EXPERIMENTAL EVIDENCE If Josephson/Coulomb model is correct, the same behavior should be observed in Josephson arrays… At non-zero field simple Josephson arrays show temperature independent resistance with values that change by orders of magnitude. (H. van der Zant et al, 1996)

SUPERCONDUCTOR-INSULATOR: EXPERIMENTAL EVIDENCE If Josephson/Coulomb model is correct, the same behavior should be observed in Josephson arrays… At non-zero field simple Josephson arrays show temperature independent resistance with values that change by orders of magnitude. (H. van der Zant et al, 1996)

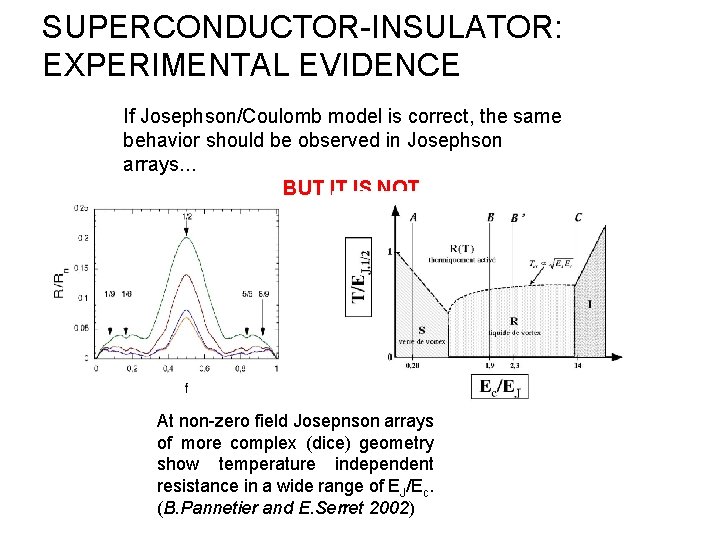
SUPERCONDUCTOR-INSULATOR: EXPERIMENTAL EVIDENCE If Josephson/Coulomb model is correct, the same behavior should be observed in Josephson arrays… BUT IT IS NOT At non-zero field Josephson arrays of more complex (dice) geometry show temperature independent resistance in a wide range of EJ/Ec. (B. Pannetier and E. Serret 2002)

Bosonic v/s Fermionic scenario ? None of them is able to describe data on In. Ox and Ti. N 3 -d scenario: competition between Cooper pairing and localization (without any role of Coulomb interaction)

Theoretical model Simplest BCS attraction model, but for critical (or weakly) localized electrons H = H 0 - g ∫ d 3 r Ψ ↑† Ψ ↓Ψ ↑ Ψ = Σ cj Ψj (r) M. Ma and P. Lee (1985) : Basis of localized eigenfunctions S-I transition at δL ≈ Tc

Superconductivity at the Localization Threshold: δL → 0 Consider Fermi energy very close to the mobility edge: single-electron states are extended but fractal and populate small fraction of the whole volume How BCS theory should be modified to account for eigenstate’s fractality ? Method: combination of analitic theory and numerical data for Anderson mobility edge model

Mean-Field Eq. for Tc

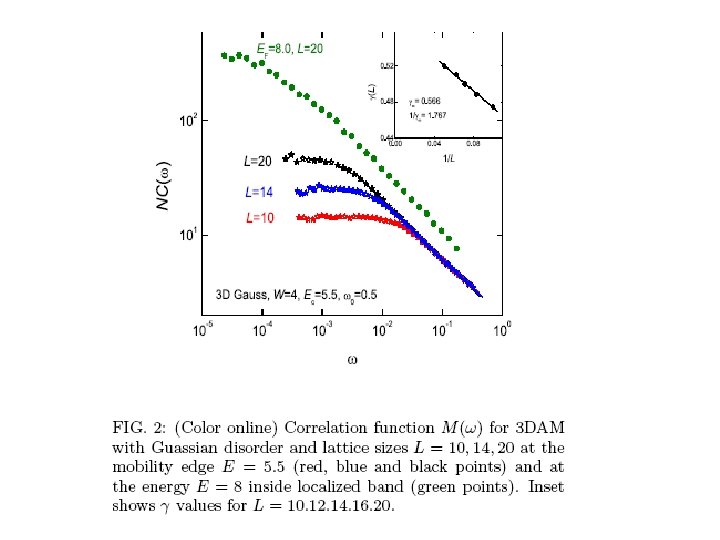
Fractality of wavefunctions IPR: Mi = D 2 ≈ 1. 3 3 D Anderson model: γ = 0. 57 4 dr in 3 D

Modified mean-field approximation for critical temperature Tc For small this Tc is higher than BCS value !

Order parameter in real space for ξ = ξk SC fraction =

Superconductivity with Pseudogap Now we move Fermi- level into the range of localized eigenstates Local pairing in addition to collective pairing

Local pairing energy 1. Parity gap in ultrasmall grains K. Matveev and A. Larkin 1997 ------- EF --↑↓--- ↓-- No many-body correlations Correlations between pairs of electrons localized in the same “orbital”

2. Parity gap for Andersonlocalized eigenstates Energy of two single-particle excitations after depairing:

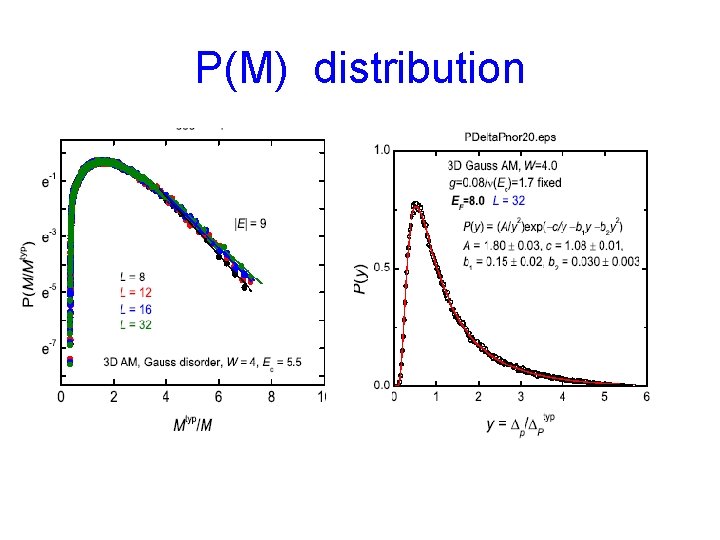
P(M) distribution

Critical temperature in the pseudogap regime MFA: Here we use M(ω) specific for localized states MFA is OK as long as is large

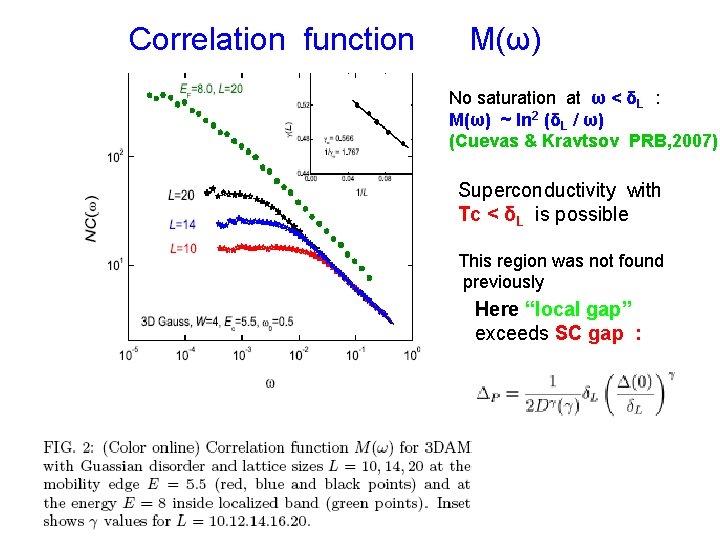
Correlation function M(ω) No saturation at ω < δL : M(ω) ~ ln 2 (δL / ω) (Cuevas & Kravtsov PRB, 2007) Superconductivity with Tc < δL is possible This region was not found previously Here “local gap” exceeds SC gap :

MFA: Critical temperature in the pseudogap regime We need to estimate ~ ( 3 ) It is nearly constant in a very broad range of

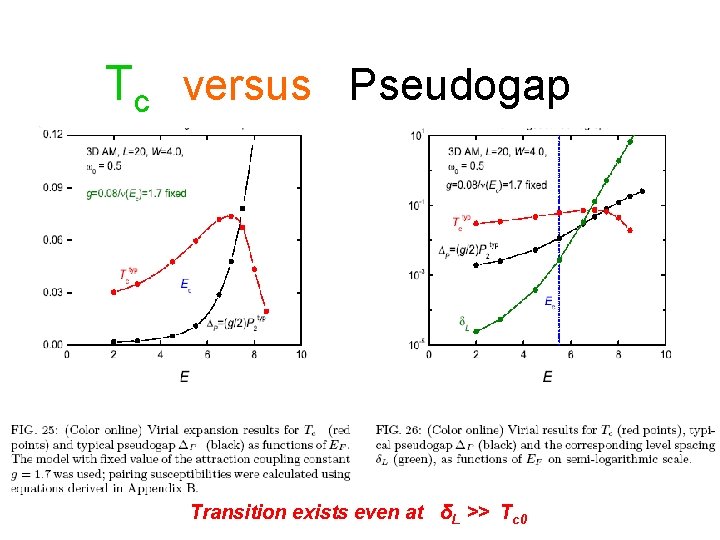
Tc versus Pseudogap Transition exists even at δL >> Tc 0

Single-electron states suppressed by pseudogap “Pseudospin” approximation Effective number of interacting neighbours

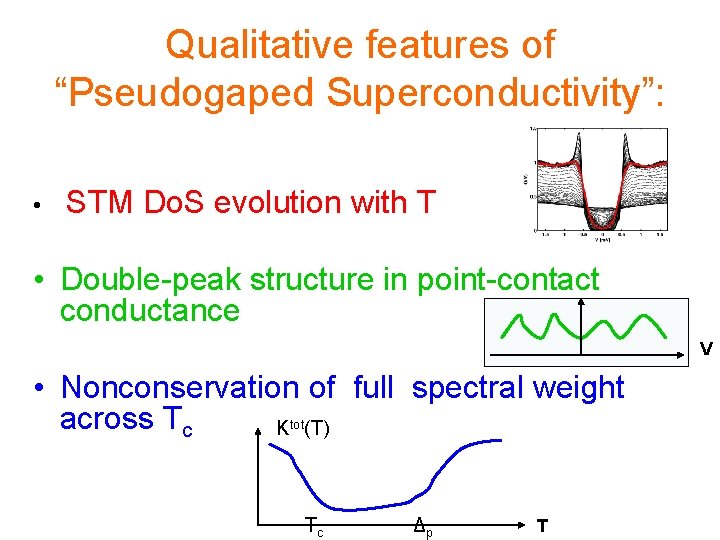
Qualitative features of “Pseudogaped Superconductivity”: • STM Do. S evolution with T • Double-peak structure in point-contact conductance V • Nonconservation of full spectral weight across Tc Ktot(T) Tc Δp T

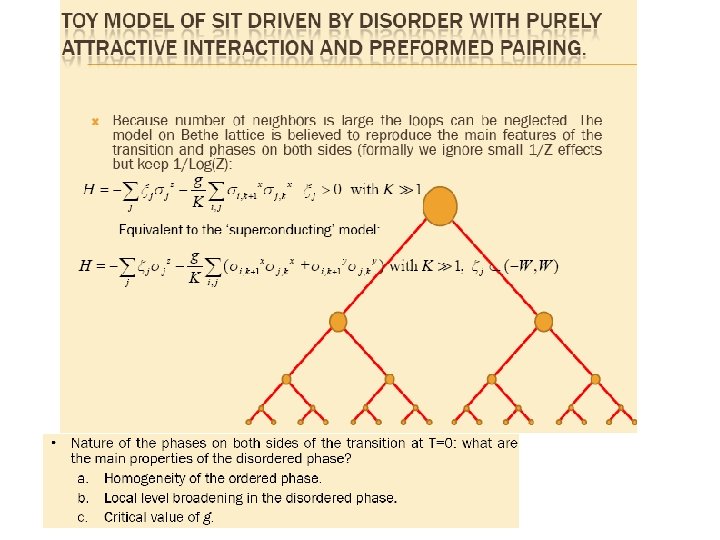
Third Scenario • Bosonic mechanism: preformed Cooper pairs + competition Josephson v/s Coulomb – S I T in arrays • Fermionic mechanism: suppressed Cooper attraction, no paring – S M T • Pseudospin mechanism: individually localized pairs - S I T in amorphous media SIT occurs at small Z and lead to paired insulator How to describe this quantum phase transition ? Cayley tree model is solved (L. Ioffe & M. Mezard)

Superconductor-Insulator Transition Simplified model of competition between random local energies (ξi. Siz term) and XY coupling

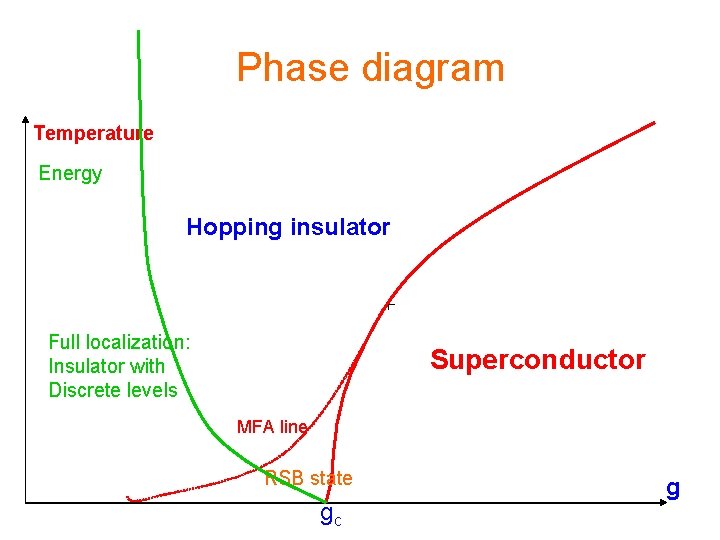
Phase diagram Temperature Energy Hopping insulator Full localization: Insulator with Discrete levels Superconductor MFA line RSB state gc g

Fixed activation energy is due to the absence of thermal bath at low ω

Conclusions Pairing on nearly-critical states produces fractal superconductivity with relatively high Tc but very small superconductive density Pairing of electrons on localized states leads to hard gap and Arrhenius resistivity for 1 e transport Pseudogap behaviour is generic near S-I transition, with “insulating gap” above Tc New type of S-I phase transition is described (on Cayley tree, at least). On insulating side activation of pair transport is due to Many. Body. Localization threshold

Coulomb enchancement near mobility edge ? ? Normally, Coulomb interaction is overscreened, with universal effective coupling constant ~ 1 Condition of universal screening: Example of a-In. Ox Effective Couloomb potential is weak:

Alternative method to find Tc: Virial expansion (A. Larkin & D. Khmelnitsky 1970)

Neglected : off-diagonal terms Non-pair-wise terms with 3 or 4 different eigenstates were omitted To estimate the accuracy we derived effective Ginzburg. Landau functional taking these terms into account

Tunnelling Do. S Average Do. S: Asymmetry in local Do. S:

Superconductivity at the Mobility Edge: major features - Critical temperature Tc is well-defined through the whole system in spite of strong Δ(r) fluctuations - Local Do. S strongly fluctuates in real space; it results in asymmetric tunnel conductance G(V, r) ≠ G(-V, r) - Both thermal (Gi) and mesoscopic (Gid) fluctuational parameters of the GL functional are of order unity

Tc from 3 different calculations Modified MFA equation leads to: BCS theory: Tc = ωD exp(-1/ λ)

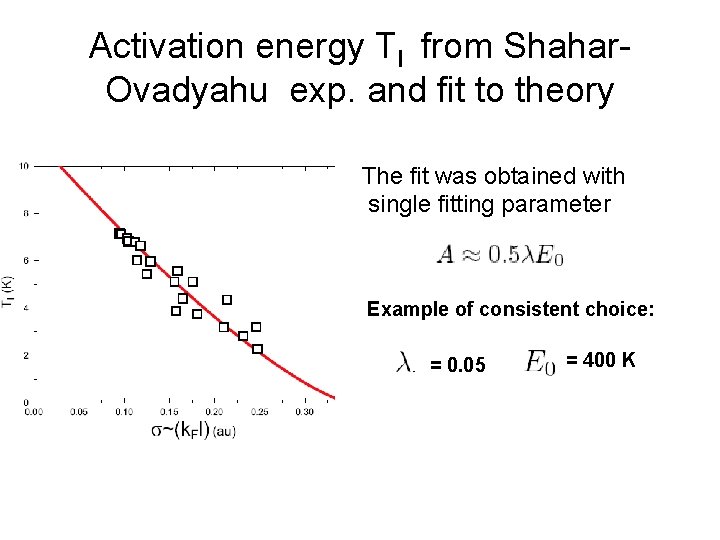
Activation energy TI from Shahar. Ovadyahu exp. and fit to theory The fit was obtained with single fitting parameter Example of consistent choice: = 0. 05 = 400 K