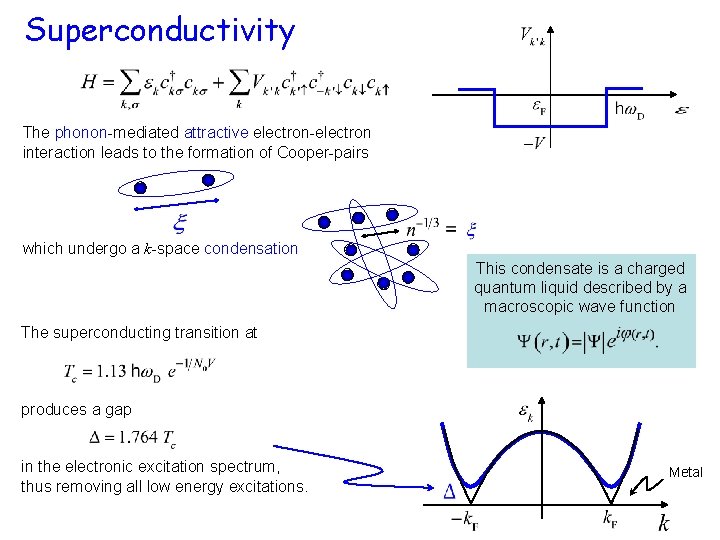
Superconductivity Superconductivity The phononmediated attractive electronelectron interaction leads



![Classical & quantum limits charge phase 0 current action Hamiltonian [N, ] = i Classical & quantum limits charge phase 0 current action Hamiltonian [N, ] = i](https://slidetodoc.com/presentation_image_h/026bb9e855f7fd7865eb11274f4960f7/image-6.jpg)
























- Slides: 52

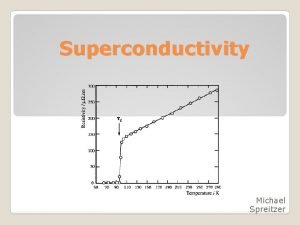
Superconductivity

Superconductivity The phonon-mediated attractive electron-electron interaction leads to the formation of Cooper-pairs which undergo a k-space condensation This condensate is a charged quantum liquid described by a macroscopic wave function The superconducting transition at produces a gap in the electronic excitation spectrum, thus removing all low energy excitations. Metal

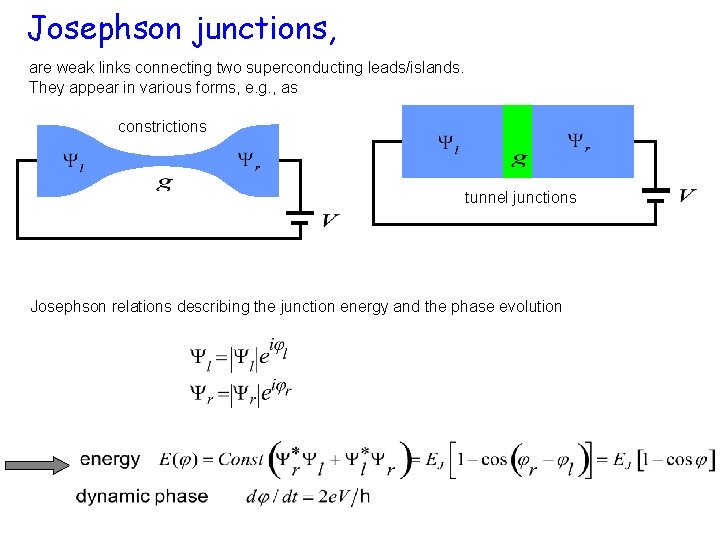
Josephson junctions

Josephson junctions, are weak links connecting two superconducting leads/islands. They appear in various forms, e. g. , as constrictions tunnel junctions Josephson relations describing the junction energy and the phase evolution

Two energy scales charge phase 0 current The particle number N = Q/2 e and the phase are conjugate variables, i. e. , we have a particle - phase duality [N, ] = i (Anderson) Fock space fixed phase fixed charge Q=2 e. N
![Classical quantum limits charge phase 0 current action Hamiltonian N i Classical & quantum limits charge phase 0 current action Hamiltonian [N, ] = i](https://slidetodoc.com/presentation_image_h/026bb9e855f7fd7865eb11274f4960f7/image-6.jpg)
Classical & quantum limits charge phase 0 current action Hamiltonian [N, ] = i

Classical limit: gauge invariance and fluxoid quantization in a loop H � 2 unique gauge invariant phases kinetic energy of currents ( ) Free energy of a loop with inductance L: 1 junction: 2 junctions: In a small inductance loop, In a large inductance loop,

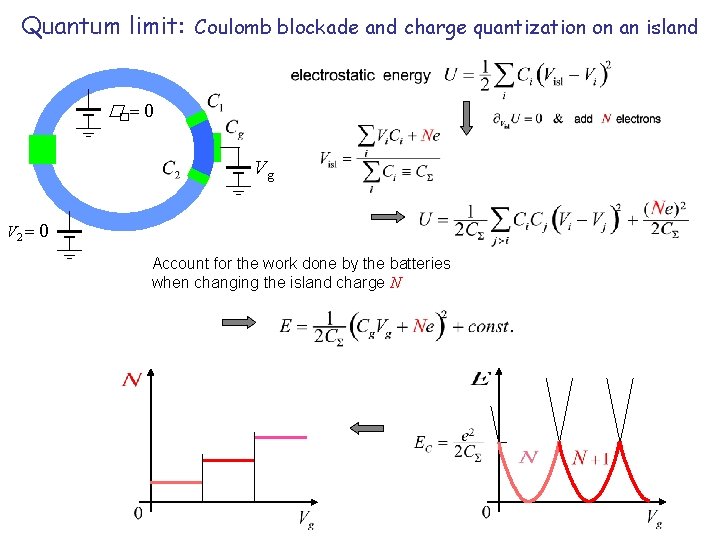
Quantum limit: Coulomb blockade and charge quantization on an island V� Vn V 2

Quantum limit: Coulomb blockade and charge quantization on an island ��= 0 Vg V 2 = 0 Account for the work done by the batteries when changing the island charge N

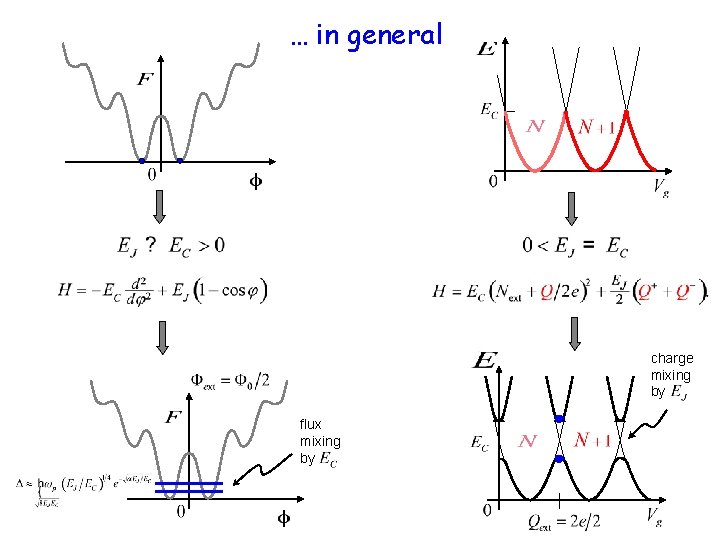
… in general charge mixing by flux mixing by

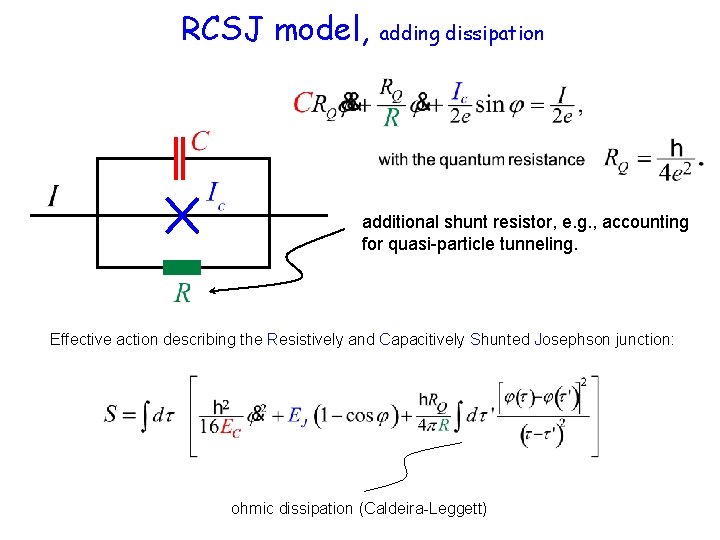
RCSJ model, adding dissipation additional shunt resistor, e. g. , accounting for quasi-particle tunneling. Effective action describing the Resistively and Capacitively Shunted Josephson junction: ohmic dissipation (Caldeira-Leggett)

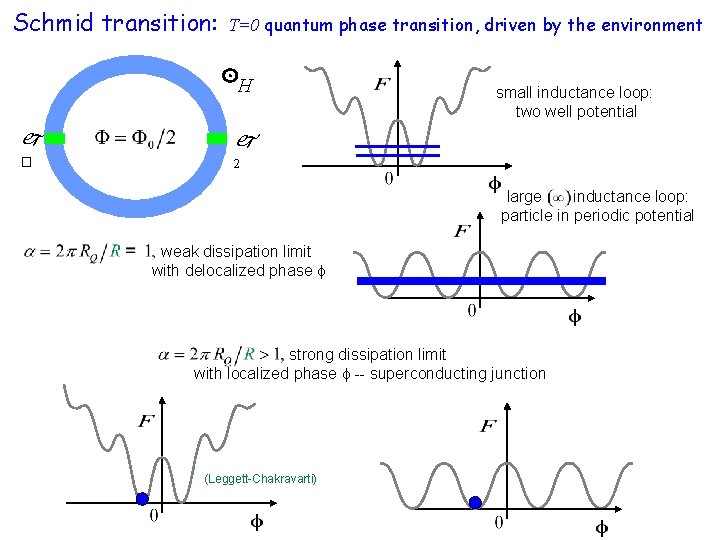
Schmid transition: T=0 quantum phase transition, driven by the environment H � 2 small inductance loop: two well potential large inductance loop: particle in periodic potential weak dissipation limit with delocalized phase strong dissipation limit with localized phase -- superconducting junction (Leggett-Chakravarti)

classical computing

Mechanics First `Programmer’ and Inventor of the Difference Engine 1834 Ada Byron, Lady Lovelace 1815 -1852 The `full’ version of this machine was built in 1991 by the Science Museum, London Enigma, cracked by Alan Turing with help of COLOSSUS Charles Babbage 1791 -1871

Electronics The ENIAC (Electronic Numerical Integrator and Computer) computer was built in 1946 Built at University of Pennsylvania, it included 18’ 000 tubes, weighed 30 tons, required 6 operators, and 160 m 2 of space.

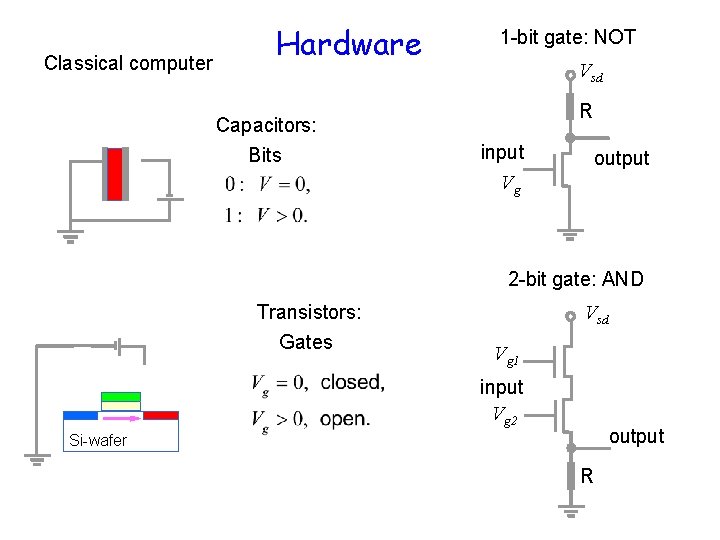
Classical computer Hardware Capacitors: Bits 1 -bit gate: NOT Vsd R input Vg output 2 -bit gate: AND Transistors: Gates Vsd Vg 1 input Vg 2 output Si-wafer R

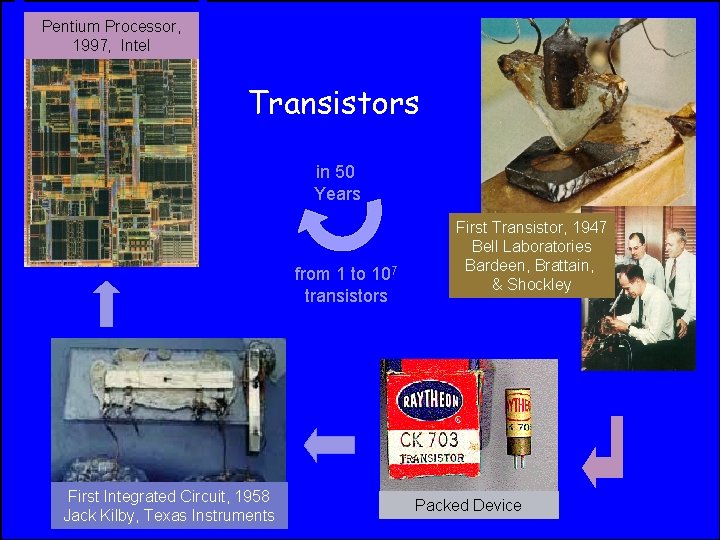
Pentium Processor, 1997, Intel Transistors in 50 Years from 1 to 107 transistors First Integrated Circuit, 1958 Jack Kilby, Texas Instruments First Transistor, 1947 Bell Laboratories Bardeen, Brattain, & Shockley Packed Device

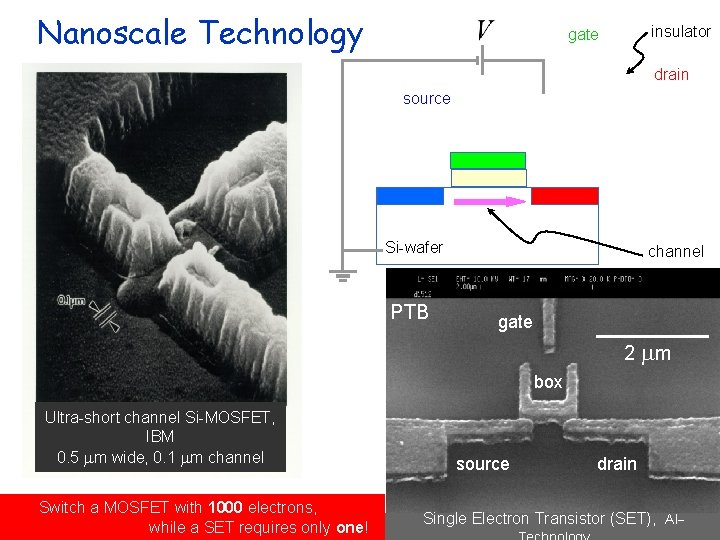
Nanoscale Technology insulator gate drain source Si-wafer PTB channel gate 2 mm box Ultra-short channel Si-MOSFET, IBM 0. 5 mm wide, 0. 1 mm channel Switch a MOSFET with 1000 electrons, while a SET requires only one! source drain Single Electron Transistor (SET), Al-

Applications Your track control in the car Classical computers solve any computational task …. . Your bank account Your washing machine Your agenda Your science …. but some are really hard !

Computational Complexity An input x is quantified via its information content L = log 2 x. A calculation is characterized by the number s of steps (logical gates) involved. A problem is class P (efficiently solvable) if s is polynomial in L, A problem is deemed `hard’ (not in P) if s scales exponentially in L, A `classic’ hard problem is that of prime factorization: given a non-prime number N, find its factors; the best known algorithm scales as s ~ exp (2 L 1/3 (ln. L)2/3). A modern computer can factor a 130 -decimal-digits number (L = 300) in a few weeks - days; 1827365426354265930284950398726453672819048374987653426354857645283905612849667483920396069782635471628694637109586756325221365901 doubling L would take millions of years to carry out this calculation. A quantum computer would do the job within minutes

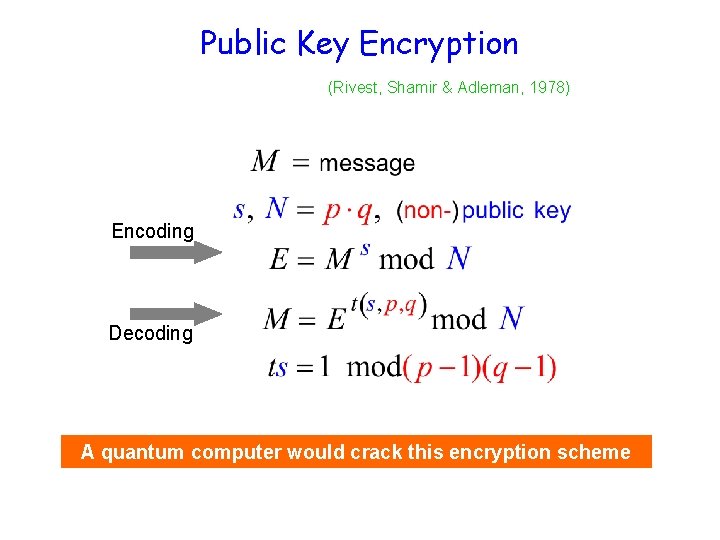
Public Key Encryption (Rivest, Shamir & Adleman, 1978) Encoding Decoding A quantum computer would crack this encryption scheme

Quantum computing

``…nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical…” R. Feynman If one has N quantum two level systems (e. g. L spins) they can have different states. To describe such a system in classical computer one needs to have complex numbers, that requires exponentially large computational resources. Thus modeling even small quantum system on a classical computer is practically impossible task. But since Nature does it very efficiently one can try to use its ability to deal with quantum systems and to apply it also for computational problem.

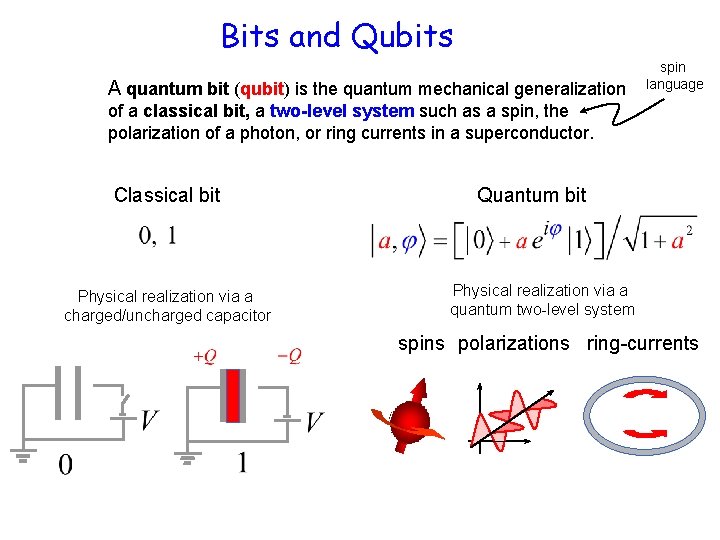
Bits and Qubits A quantum bit (qubit) is the quantum mechanical generalization spin language of a classical bit, a two-level system such as a spin, the polarization of a photon, or ring currents in a superconductor. Classical bit Physical realization via a charged/uncharged capacitor Quantum bit Physical realization via a quantum two-level system spins polarizations ring-currents

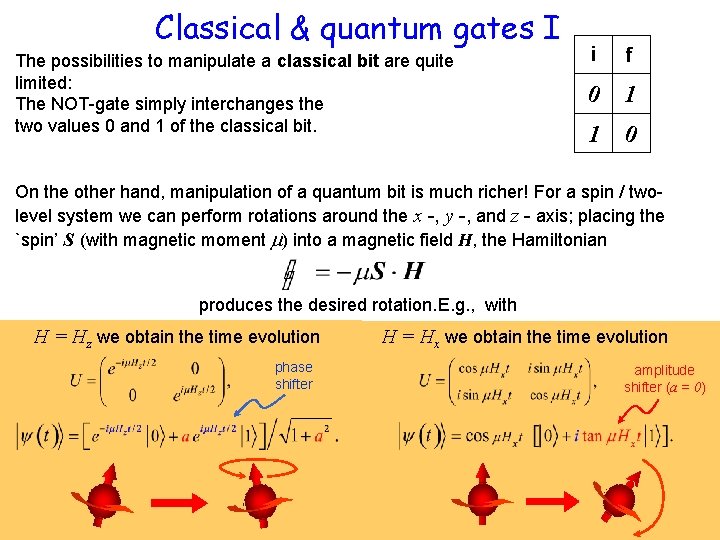
Classical & quantum gates I The possibilities to manipulate a classical bit are quite limited: The NOT-gate simply interchanges the two values 0 and 1 of the classical bit. i f 0 1 1 0 On the other hand, manipulation of a quantum bit is much richer! For a spin / twolevel system we can perform rotations around the x -, y -, and z - axis; placing the `spin’ S (with magnetic moment ) into a magnetic field H, the Hamiltonian with produces the desired rotation. E. g. , …. H = Hz we obtain the time evolution phase shifter H = Hx we obtain the time evolution amplitude shifter (a = 0)

Classical & quantum gates II NOT The combination of the classical gates allows us to construct all manipulations on classical bits. i f 0 1 1 0 Is there a set of universal quantum gates ? How does such a set look like ? irreversible AND i 0 0 1 1 i 0 1 f 0 0 0 1 OR i 0 0 1 1 i 0 1 f 0 1 1 1 Two-qubit gate: XOR (CNOT) Single-qubit gates: Rotations The target flips if the control is on 1 amplitude shifter Hadamard (basis change): i 0 0 1 1 phase shifter H control target i 0 1 f 0 1 1 0

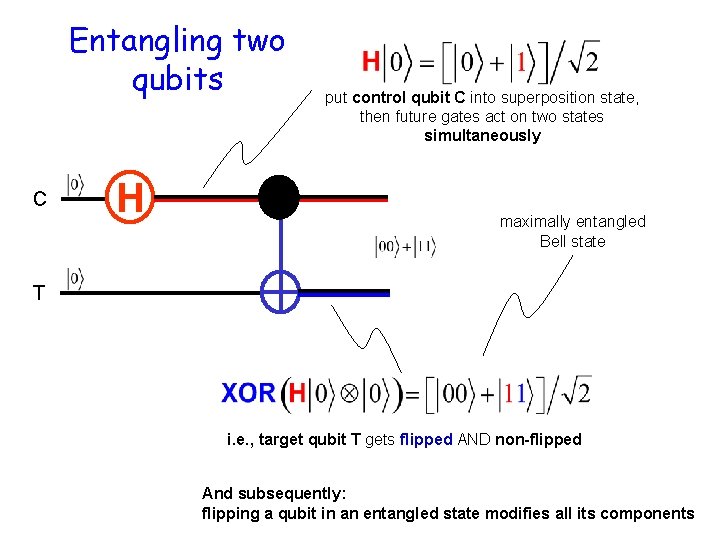
Entangling two qubits C H put control qubit C into superposition state, then future gates act on two states simultaneously maximally entangled Bell state T i. e. , target qubit T gets flipped AND non-flipped And subsequently: flipping a qubit in an entangled state modifies all its components

Quantum Algorithms

Quantum algorithms Shor’s Factorization algorithm (1994) finds prime factors in polynomial, rather than exponential time. Grover’s Search algorithm (1997) searches unstructured database (e. g. telephone book) of N entries by steps.

Although Grover’s algorithm doesn’t change complexity class it is not less fundamental, than Shor’s algorithm. (i) It is not hard to prove, that classical algorithms can do no better, than just straight search through the list, requiring on average N/2 steps (ii) The `quantum speed-up’ ~ is greater than that achieved by Shor’s factorization algorithm (iii) One can show, that no quantum algorithm can do better, than thus it is optimal! ,

Grover’s Search algorithm Task: Given an unstructured set of elements, find the one, that corresponds to the answer of some question. The Algorithm Assume that the database contains N elements, N is some power of 2. Let there be only one solution, that we are looking for. We start with a homogeneous superposition of all basis states This can be achieved, e. g. , by starting with n qubits in the state Hadamard transform The goal is to to increase the amplitude of the component and applying the

The algorithm will iterate the Grover rotation G a certain number of times to obtain state very close to. The Grover rotation consists of two parts: an oracle call and a reflection about. The oracle call is just quantum implementation of searching. There must exist unitary operator

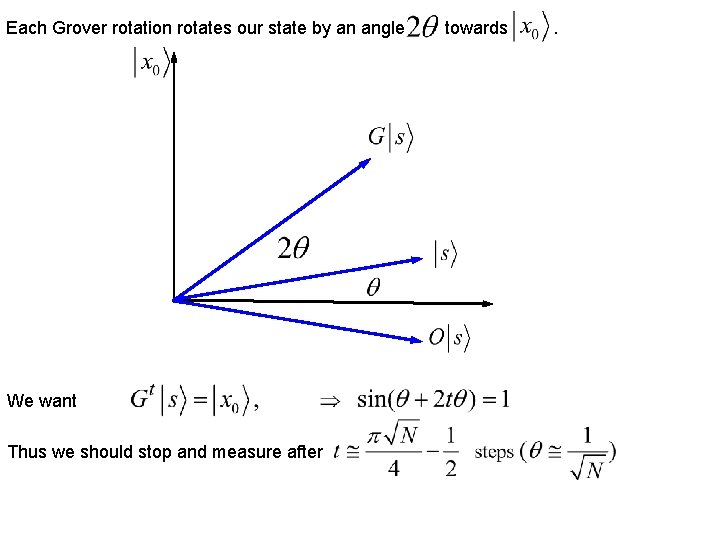
Each Grover rotation rotates our state by an angle We want Thus we should stop and measure after towards .

Quantum Hardware

Physical implementation All hardware implementations of quantum computers have to deal with the conflicting requirements of controllability while minimizing the coupling to the environment in order to avoid decoherence. Solid state implementations enjoy good scalability & variability but require careful designs in order to avoid decoherence when trying to build Schrödinger cats

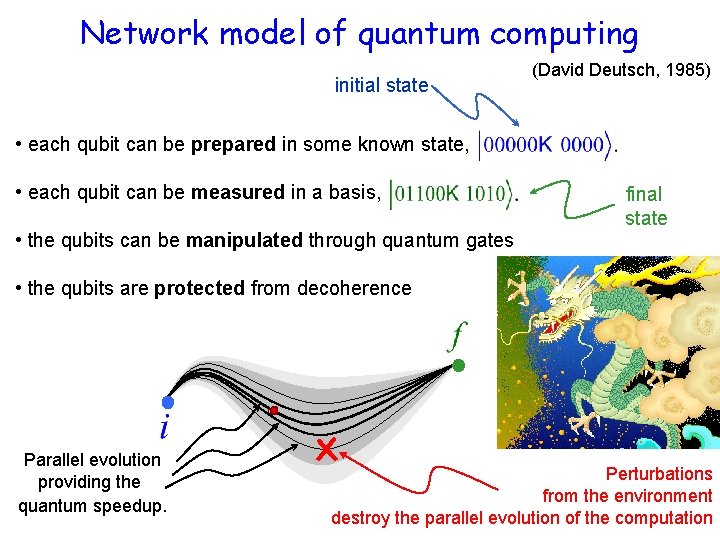
Network model of quantum computing initial state (David Deutsch, 1985) • each qubit can be prepared in some known state, • each qubit can be measured in a basis, • the qubits can be manipulated through quantum gates final state • the qubits are protected from decoherence Parallel evolution providing the quantum speedup. Perturbations from the environment destroy the parallel evolution of the computation

Physical implementations Quantum optics, NMR-schemes Good decoupling & precision: • trapped atoms (Cirac & Zoller) • photons in QED cavities (Monroe ea, Turchette ea) • molecular NMR (Gershenfeld & Chuang) • 31 P in silicon (Kane) Solid state implementations Good scalability & variability: • spins on quantum dots (Loss & Di. Vincenzo) • 31 P in silicon (Kane) • Josephson junctions, charge (Schön ea, Averin phase (Bocko ea, Mooij ea) All hardware implementations of quantum computers have to deal with the conflicting requirements of controllability while minimizing the coupling to the environment in order to avoid decoherence. Have to deal with individual atoms, photons, spins, …… Problems with control, interconnections, measurements. Have to deal with many degrees of freedom. Problems with decoherence.

The rules of the game achievements Find a system which emulates a spin / quantum two-level system and • which remains coherent Quantum optics not a problem Condensed Matter up to Q ~ 104 • which can be manipulated (rotations) • which can be interconnected and entangled with other qubits Condensed Matter 2 charge qubits, interacting Quantum optics 4 9 Be ions, deterministic • which can be projected (measured) • which carries out an algorithm (e. g. , Shor’s prime factorization) Quantum optics Bell inequailty checks NMR 15 = 3 * 5

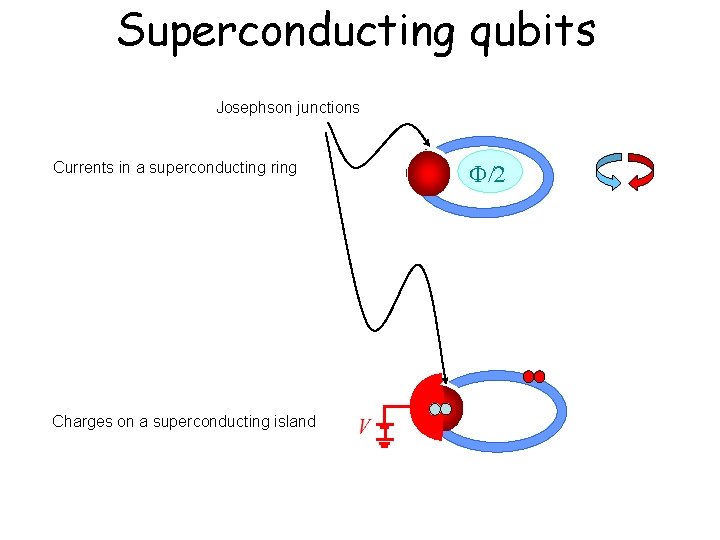
Superconducting quantum bits

Superconducting qubits Josephson junctions Currents in a superconducting ring Charges on a superconducting island /2

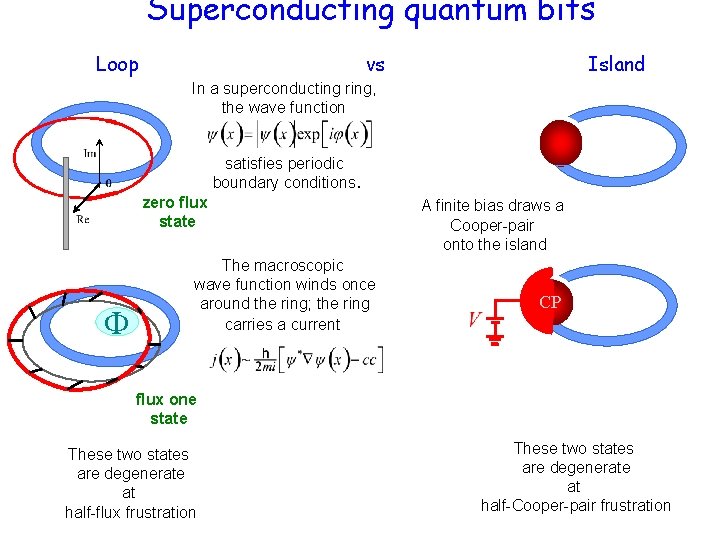
Superconducting quantum bits Loop vs Island In a superconducting ring, the wave function satisfies periodic boundary conditions. zero flux state The macroscopic wave function winds once around the ring; the ring carries a current A finite bias draws a Cooper-pair onto the island CP flux one state These two states are degenerate at half-flux frustration These two states are degenerate at half-Cooper-pair frustration

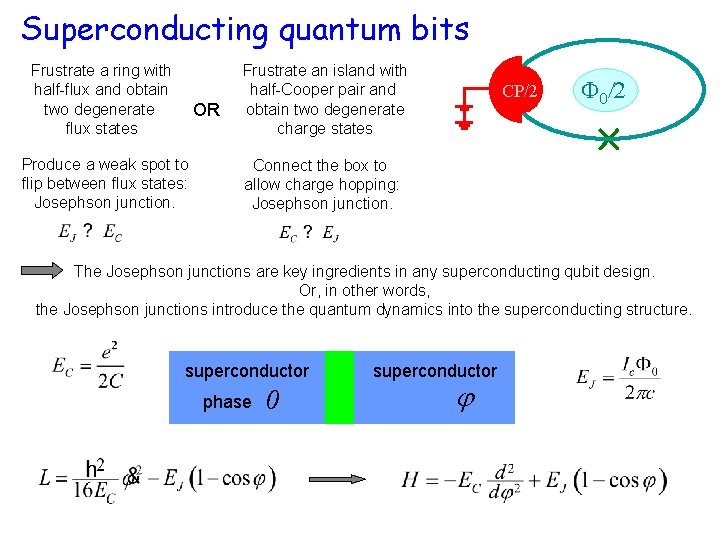
Superconducting quantum bits Frustrate a ring with half-flux and obtain two degenerate flux states OR Produce a weak spot to flip between flux states: Josephson junction. Frustrate an island with half-Cooper pair and obtain two degenerate charge states CP/2 0/2 Connect the box to allow charge hopping: Josephson junction. The Josephson junctions are key ingredients in any superconducting qubit design. Or, in other words, the Josephson junctions introduce the quantum dynamics into the superconducting structure. superconductor phase 0 superconductor

Three types Charge Schön et al. Averin 1997 Josephson Flux/Phase Ioffe et al. Orlando et al. 1999 Bocko et al. 1997 charge mixing by superconductor phase 0 V phase states

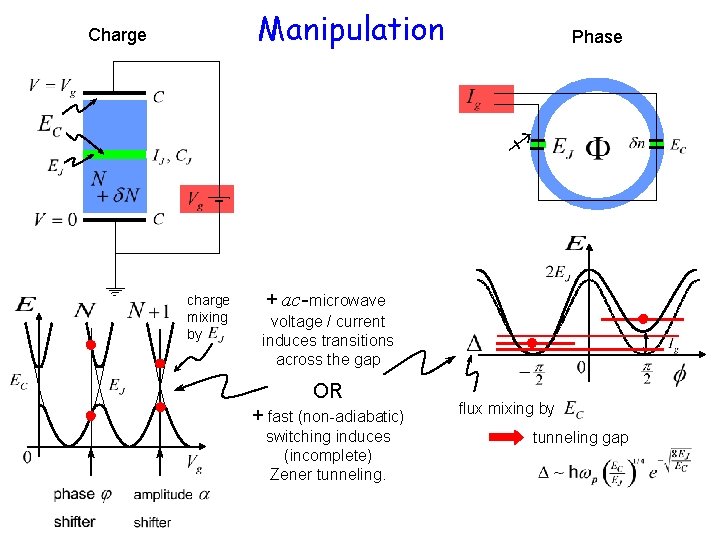
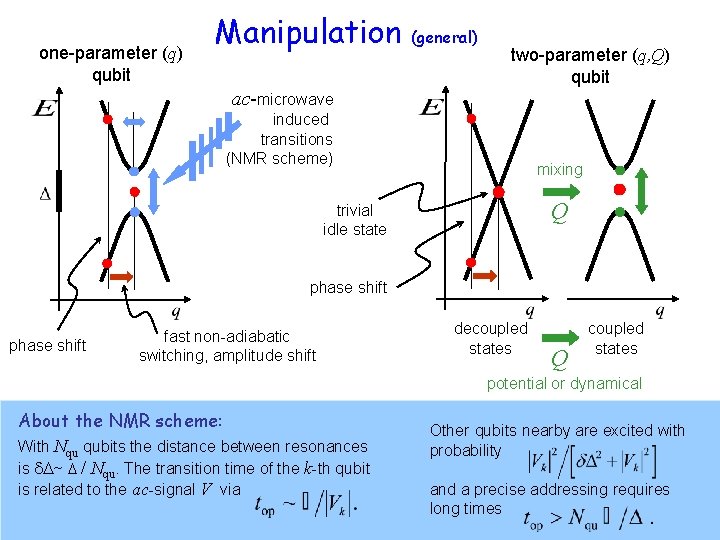
Manipulation

Manipulation Charge Phase charge mixing by + ac-microwave voltage / current induces transitions across the gap OR + fast (non-adiabatic) switching induces (incomplete) Zener tunneling. flux mixing by tunneling gap

one-parameter (q) qubit Manipulation (general) two-parameter (q, Q) qubit ac-microwave induced transitions (NMR scheme) mixing Q trivial idle state phase shift fast non-adiabatic switching, amplitude shift decoupled states Q coupled states potential or dynamical About the NMR scheme: With Nqu qubits the distance between resonances is ~ / Nqu. The transition time of the k-th qubit is related to the ac-signal V via Other qubits nearby are excited with probability and a precise addressing requires long times

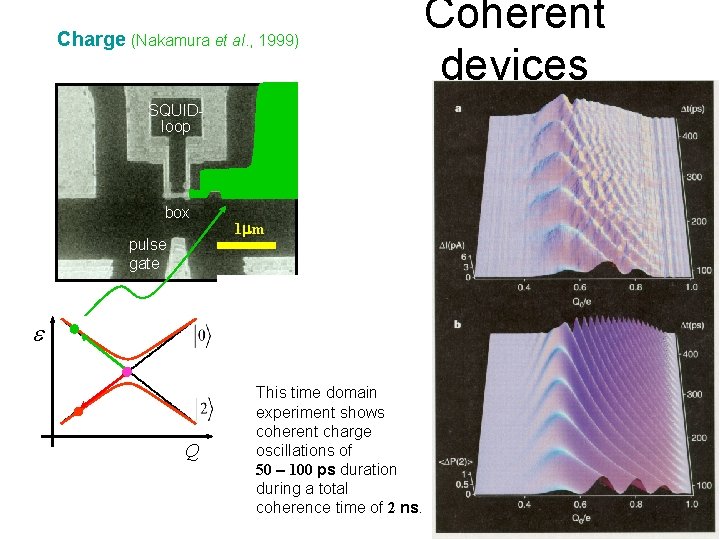
Coherent devices Charge (Nakamura et al. , 1999) SQUIDloop detector box pulse gate 1 m Q e fast gate voltage pulse Q time

Charge (Nakamura et al. , 1999) SQUIDloop detector box pulse gate 1 m Q e Q This time domain time fast gate experiment shows voltage pulse coherent charge oscillations of 50 - 100 ps duration during a total coherence time of 2 ns. Coherent devices

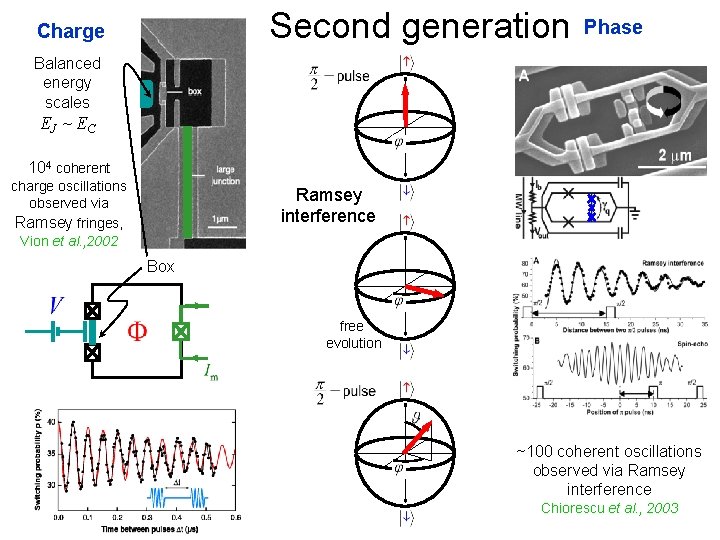
Second generation Charge Phase Balanced energy scales EJ ~ EC 104 coherent charge oscillations observed via Ramsey fringes, Vion et al. , 2002 Ramsey interference Box free evolution ~100 coherent oscillations observed via Ramsey interference Chiorescu et al. , 2003

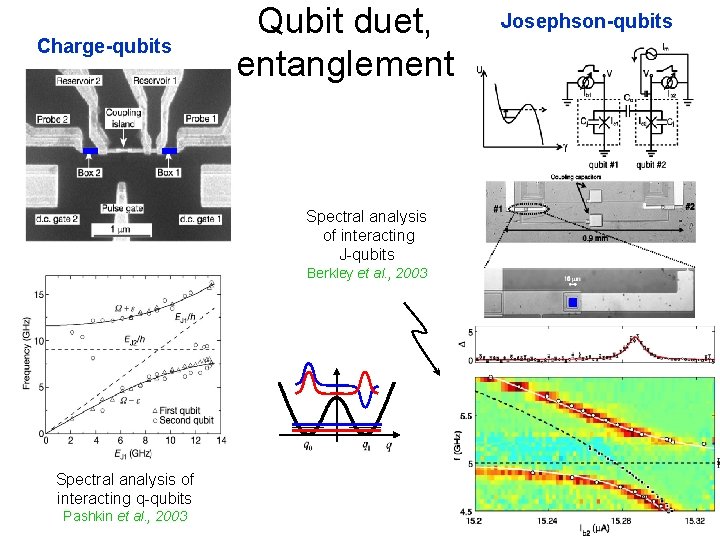
Charge-qubits Qubit duet, entanglement Spectral analysis of interacting J-qubits Berkley et al. , 2003 Spectral analysis of interacting q-qubits Pashkin et al. , 2003 Josephson-qubits

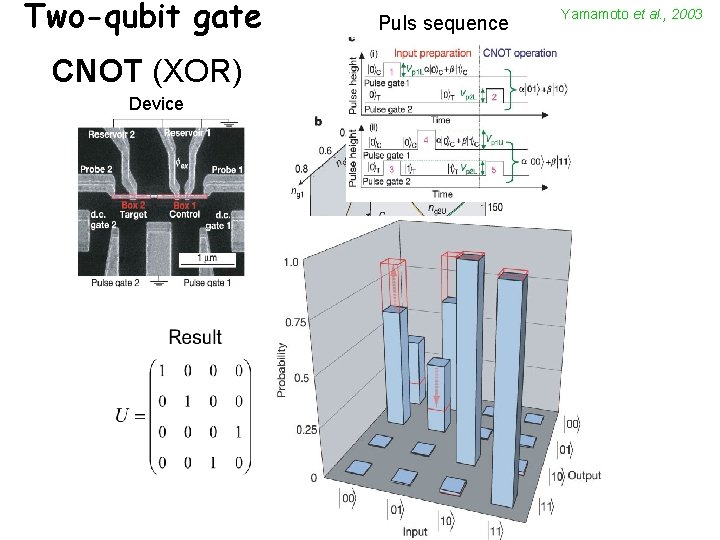
Two-qubit gate CNOT (XOR) Device Puls sequence Yamamoto et al. , 2003

The End
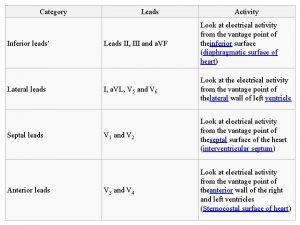
 Pathologic q wave criteria
Pathologic q wave criteria Superconductivity
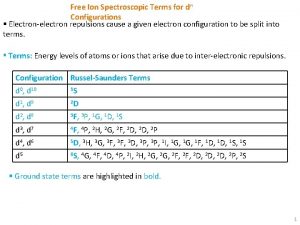
Superconductivity Superconductivity
Superconductivity Superconductivity
Superconductivity Superconductivity a level physics
Superconductivity a level physics Superconductivity
Superconductivity Superconductivity
Superconductivity What are superconductors
What are superconductors Superconductivity
Superconductivity Superconductivity
Superconductivity Types of superconductors
Types of superconductors Pining
Pining Superconductivity
Superconductivity Attractive force
Attractive force Vander waals force
Vander waals force Mullins seven domains model
Mullins seven domains model Comparative of inferiority short adjectives
Comparative of inferiority short adjectives Intra vs intermolecular
Intra vs intermolecular Attractive meaning
Attractive meaning The seven domains of attractive opportunities
The seven domains of attractive opportunities Intermolecular and intramolecular forces
Intermolecular and intramolecular forces Attractive forces
Attractive forces Attractive sce
Attractive sce Most powerful parser
Most powerful parser Seven domains of attractive opportunities
Seven domains of attractive opportunities How do companies identify attractive market segments
How do companies identify attractive market segments Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Các môn thể thao bắt đầu bằng tiếng đua
Các môn thể thao bắt đầu bằng tiếng đua Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Slidetodoc
Slidetodoc So nguyen to
So nguyen to Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Tia chieu sa te
Tia chieu sa te Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Sơ đồ cơ thể người
Sơ đồ cơ thể người Tư thế ngồi viết
Tư thế ngồi viết đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Bổ thể
Bổ thể Tư thế worms-breton
Tư thế worms-breton Tư thế ngồi viết
Tư thế ngồi viết ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Cái miệng nó xinh thế
Cái miệng nó xinh thế