Online list colouring of graphs Xuding Zhu Zhejiang

On-line list colouring of graphs Xuding Zhu Zhejiang Normal University 2016. 8. 23 CAM Hongkong

A scheduling problem: There are six basketball teams, each needs to compete with all the others. Each team can play one game per day How many days are needed to schedule all the games? Answer: 5 days

1 st day

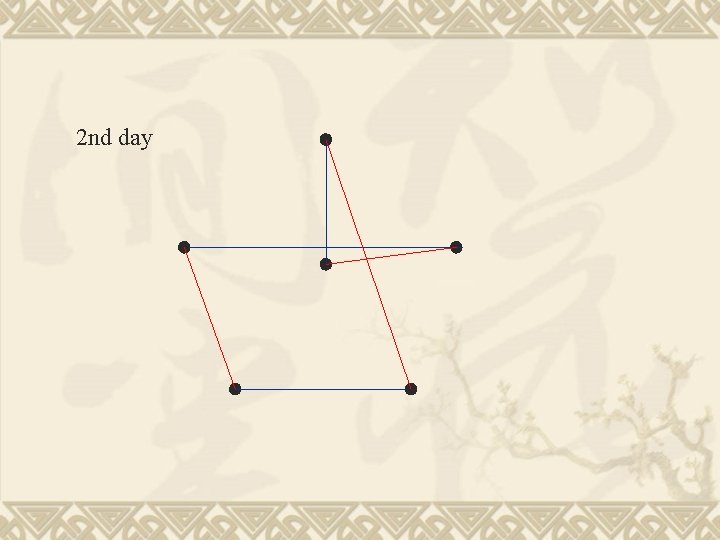
2 nd day

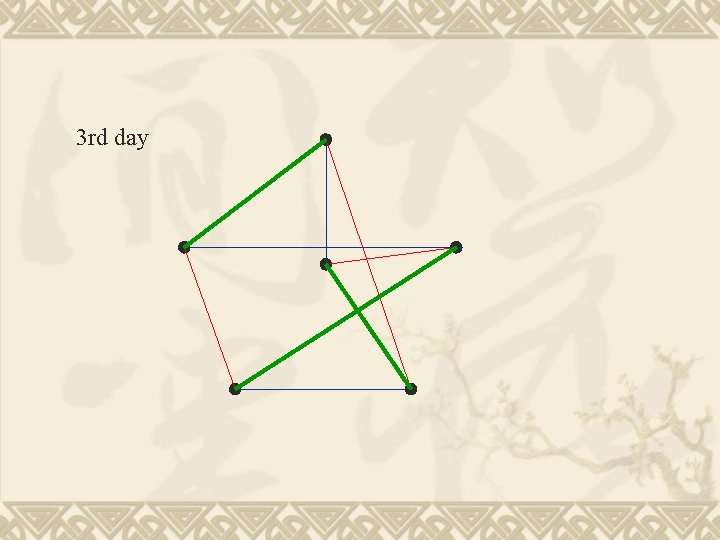
3 rd day

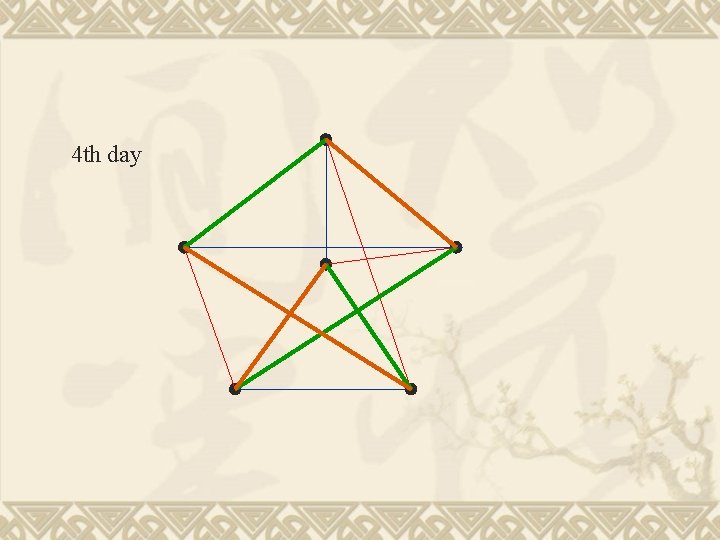
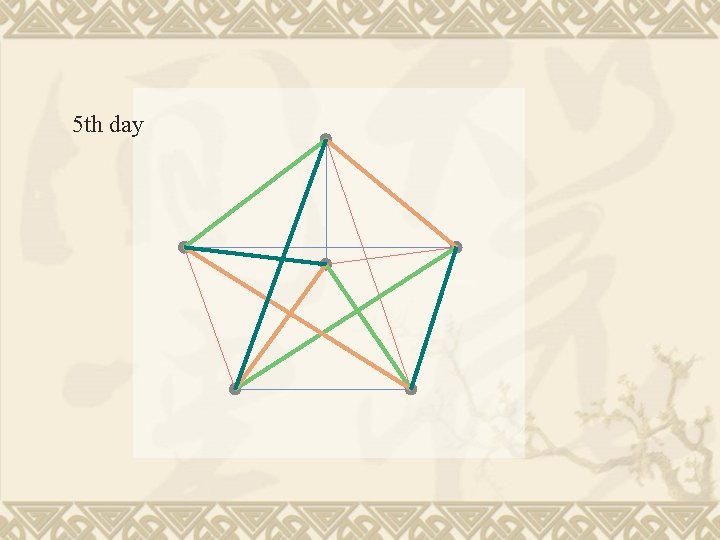
4 th day

5 th day

This is an edge colouring problem. Each edge is a game. Each day is a colour.

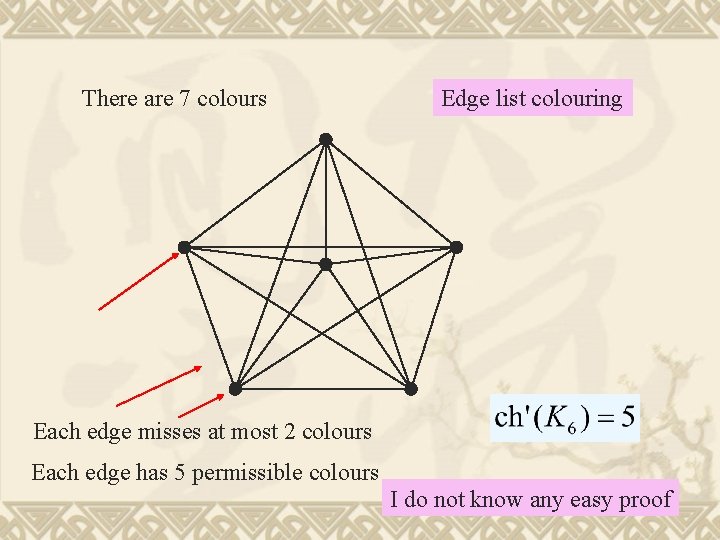
A scheduling problem: There are six basketball teams, each needs to compete with all the others. Each team can play one game per day Each team can choose one day off How many days are needed to schedule all the games? Answer: 5 days 7 days are enough 7 days are needed

There are 7 colours Edge list colouring Each edge misses at most 2 colours Each edge has 5 permissible colours I do not know any easy proof

List colouring conjecture: For any graph G, However, the conjecture remains open for Haggkvist-Janssen (1997) Uwe Schauz (2014)

A scheduling problem There are six teams, each needs to compete with all the others. Each team can play one game per day Each team can choose one day off How many days are needed to schedule all the games? Answer: 5 days 7 days are enough The choices are made before the scheduling

A scheduling problem There are six teams, each needs to compete with all the others. Each team can play one game per day is allowed not day to show Each team can choose one off up for one day How many days are needed to schedule all the games? On each day, we know which teams haven’t shown up today 7 days are enough but we do not know which teams will not show up tomorrow We need to schedule the games for today

On-line list colouring of graphs We start colouring the graph before having the full information of the list

is the number of permissible colours for x f-painting game (on-line list colouring game) on G Each vertex v is given f(v) tokens. Each token represents a permissible colour. But we do not know yet what is the colour. Two Players: Lister Reveals the list Painter Colours vertices

At round i Lister choose a set of uncoloured vertices, removes one token from each vertex of is the set of vertices which has colour i as a permissible colour. Painter chooses an independent subset vertices in are coloured by colour i. of

If at the end of some round, there is an uncolored vertex with no tokens left, then Lister wins. If all vertices are coloured then Painter wins the game.

G is f-paintable if Painter has a winning strategy for the f-painting game. G is k-paintable if G is f-paintable for f(x)=k for every x. The paint number of G is the minimum k for which G is k-paintable.

On-line List colouring: list colouring: Painter start colouring the graph after having the full information of the list before choice number

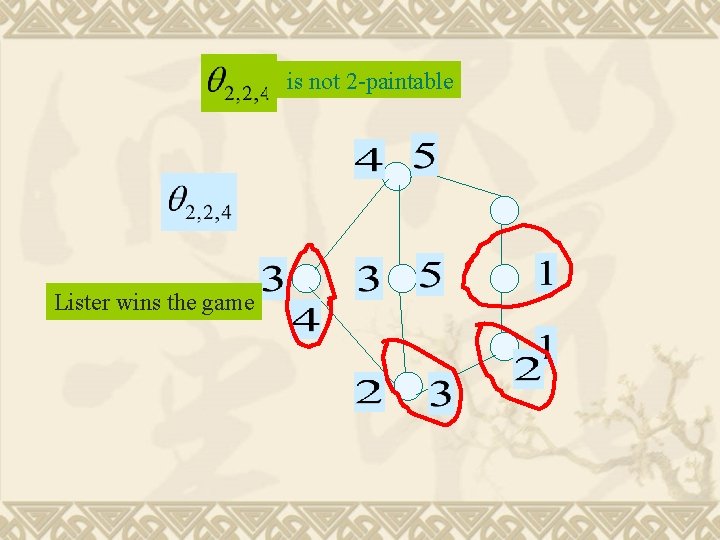
is not 2 -paintable Theorem [Erdos-Rubin-Taylor (1979)] is 2 -choosable.

is not 2 -paintable Lister wins the game

Theorem [Erdos-Rubin-Taylor, 1979] A connected graph G is 2 -choosable if and only if its core is or However, if p>1, then or is not 2 -paintable. Theorem [Zhu, 2009] A connected graph G is 2 -paintable if and only if its core is or or

Problems studied Planar graphs and locally planar graphs Chromatic-paintable graphs Complete bipartite graphs Random graphs Partial painting game b-tuple painting game and fractional paint number Defective painting game Sum-painting number of graphs

Methods: 1. Derandomize probability arguments 2. Polynomial method 3. Inductive proof 4. Kernel method 5. Probability

Complete bipartite graphs Theorem [Erdos, 1964] probabilistic proof Theorem[Zhu, 2009] If G is bipartite and has n vertices, then

A B Probability proof: Each color is assigned to vertices in A or B with probability

Initially, each vertex x has weight w(x)=1 A Assume Lister has given set If Painter colours , double the weight of each vertex in B

The total weight of uncoloured vertices is not increased. A B If a vertex is given a permissible colour but is not coloured by that colour, then its weight doubles. If x has been given k permissible colours, but remains uncoloured, then If x has able to colour it. permissible colours, Painter will be

Initially, each vertex x has weight w(x)=1 A Assume Lister has given set B If Painter colours , double the weight of each vertex in

and Theorem Erdos-Lovasz [Radha. Krishnan-Srinivasan, 2000] Conjecture Theorem [Erdos, 1964]

and Theorem Erdos-Lovasz [Radha. Krishnan-Srinivasan, 2000] Conjecture Theorem [Erdos, 1964] The proof uses a probability argument. The argument CANNOT be derandomized to give a strategy for the painting game.

and Theorem Erdos-Lovasz [Radha. Krishnan-Srinivasan, 2000] Conjecture Theorem [Erdos, 1964] Theorem [Duray-Gutowski-Kozik, 2015] Corollary

Some other results proved by derandomizing probabilistic arguments 1: Partial online list colouring

Partial painting game Partial f-painting game on G same as the f-painting game, except that Painter’s goal is not to colour all the vertices, but to colour as many vertices as possible.

Fact: Conjecture [Albertson]: Conjecture [Zhu, 2009]:

Theorem [Wong-Zhu, 2013] Conjecture [Zhu, 2009]: Proof: Derandomize a probabilistic argument

Some other results proved by derandomizing probabilistic arguments 1: Partial online list colouring 2. Fractional online choice number

b-tuple list colouring G is (a, b)-choosable if |L(v)|=a for each vertex v, then there is a b-tuple L-colouring. b-tuple on-line list colouring If each vertex has a tokens, then Painter has a strategy to colour each vertex a set of b colours.

Theorem [Alon-Tuza-Voigt, 1997] Infimum attained Probabilistic arguemnt [Gutowski, 2011] Infimum not attained

Methods: 1. Derandomize probability arguments 2. Polynomial method

paintable = deg(P(G))

Some results proved by using polynomial method

Haggkvist-Janssen (1997) Uwe Schauz (2014)

Methods: 1. Derandomize probability arguments 2. Polynomial method 3. Inductive proof

A recursive definition of f-paintable Assume (1) (2) . Then G is f-paintable, if or

Upper bounds for ch(G) proved by induction Planar graphs [ Schauz, 2009 ] Every planar graph is 5 -choosable Theorem [Thomassen, 1995] paintable

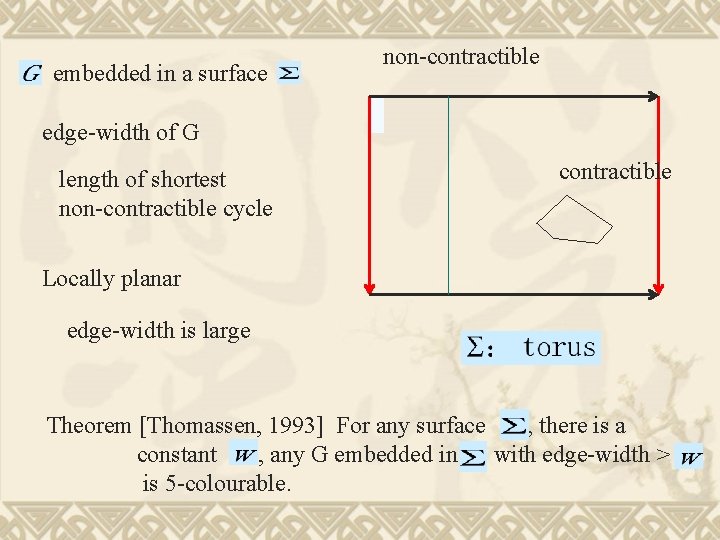
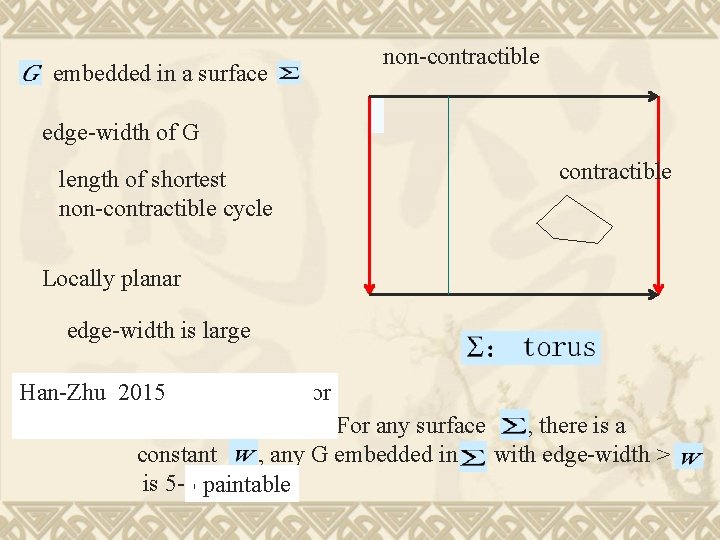
embedded in a surface non-contractible edge-width of G length of shortest non-contractible cycle contractible Locally planar edge-width is large Theorem [Thomassen, 1993] For any surface , there is a constant , any G embedded in with edge-width > is 5 -colourable.

embedded in a surface non-contractible edge-width of G length of shortest non-contractible cycle contractible Locally planar edge-width is large Han-Zhu De. Vos-Kawarabayashi-Mohor 2015 2008 Theorem [Thomassen, 1993] For any surface , there is a constant , any G embedded in with edge-width > is 5 -colourable. choosable paintable

Chromatic-paintable graphs

A graph G is chromatic choosable paintable if Conjecture: Line graphs are chromatic choosable. paintable Conjecture: Claw-free graphs are chromatic choosable. paintable Conjecture: Total graphs are chromatic choosable. paintable [Kim-Park, 2013] Conjecture: Graph squares are chromatic choosable. Theorem Ohba Conjecture: Graphs G with [Noel-Reed-Wu, 2013] are chromatic choosable. paintable

A graph G is chromatic choosable paintable if Conjecture: Line graphs are chromatic choosable. paintable Conjecture: Claw-free graphs are chromatic choosable. paintable Conjecture: Total graphs are chromatic choosable. paintable [Kim-Park, 2013] Conjecture: Graph squares are chromatic choosable. Ohba Conjecture: Graphs G with Question are chromatic choosable. paintable NO!

Theorem [Kim-Kwon-Liu-Zhu, 2012] For k>1, is not (k+1)-paintable.

is not 3 -paintable.

On-line version Huang-Wong-Zhu 2011 Ohba Conjecture: Graphs G with are chromatic choosable. paintable To prove this conjecture, we only need to consider complete multipartite graphs.

Theorem [Kozik-Micek-Zhu, 2014] On-line Ohba conjecture is true for graphs with independence number at most 3. The key in proving this theorem is to find a “good” technical statement that can be proved by induction.

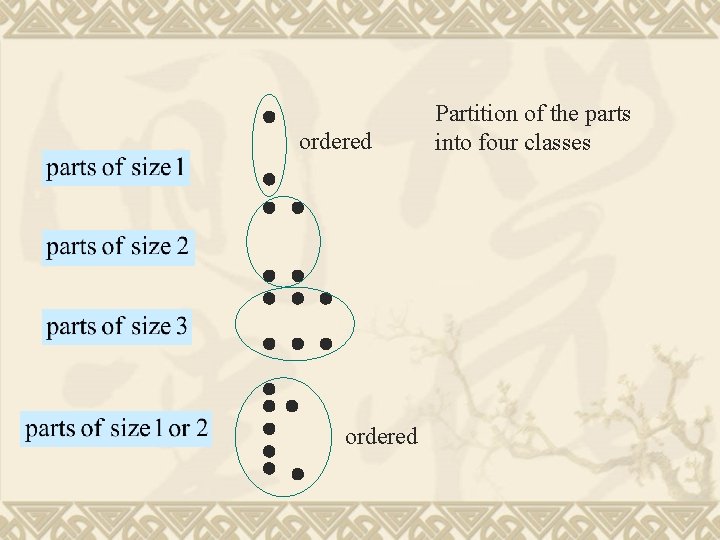
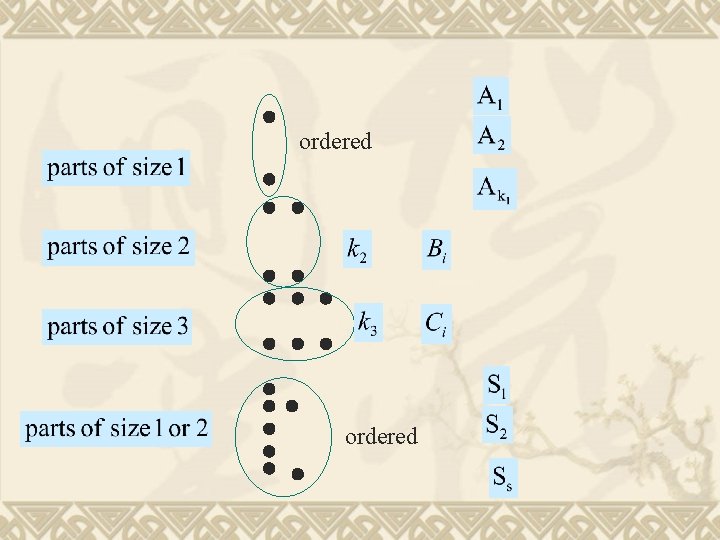
ordered Partition of the parts into four classes

ordered

G is f-paintable

Theorem [Kozik-Micek-Zhu, 2014] On-line Ohba conjecture is true for graphs with independence number at most 3. Theorem [Chang-Chen-Guo-Huang, 2014+]

d-defective painting game At round i Lister choose a set of uncoloured vertices, removes one token from each vertex of is the set of vertices which has colour i as a permissible colour. Painter chooses aansubset independent Painter of subset vertices in are coloured by colour i. of

Questions Theorem [ , , 1999] Planar graphs are 2 -defect 3 -choosable. paintable ? No! Gutowski-Han-Krawczyk-Zhu, 2016 paintable ? Yes! Han-Zhu, 2015 Theorem [Cushing-Kierstead, 2010] Planar graphs are 1 -defect 4 -choosable. paintable ? Open

Han-Zhu 2015 Locally planar graphs are 2 -defective 4 -paintable.

Methods: 1. Derandomize probability arguments 2. Polynomial method 3. Inductive proof 4. Kernel method

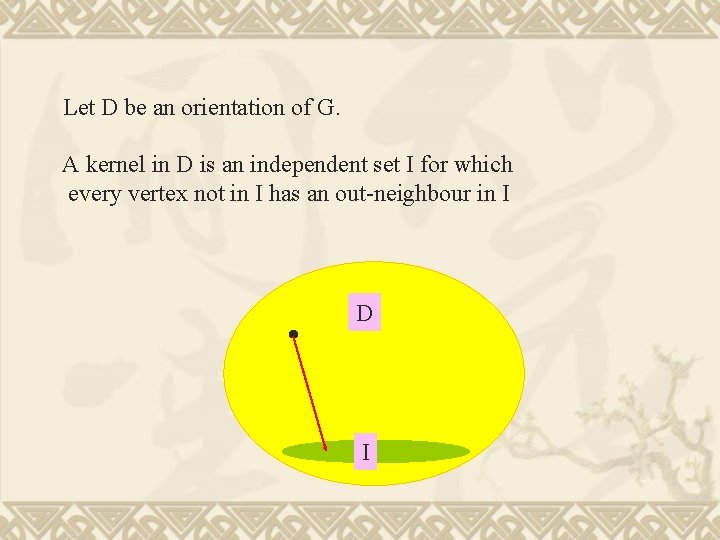
Let D be an orientation of G. A kernel in D is an independent set I for which every vertex not in I has an out-neighbour in I D I

A directed graph D is kernel perfect if every induced sub-digraph has a kernel. Theorem If G has an orientation D which is kernel perfect,

An example:

Theorem [Galvin, 1995] If G is bipartite, then

Methods: 1. Derandomize probability arguments 2. Polynomial method 3. Inductive proof 4. Kernel method 5. Probability

Theorem [Frieze, Mitsche, Perez-Gimenez, Pralat, 2015]

Theorem [Frieze, Mitsche, Perez-Gimenez, Pralat, 2015]

At each round, if Lister presents a large set M, then we are sure that M contains a large independent set I. Painter colours I. If Lister presents a small set M, then Painter randomly colours one vertex from the set.

Nine Dragon Tree Thank you

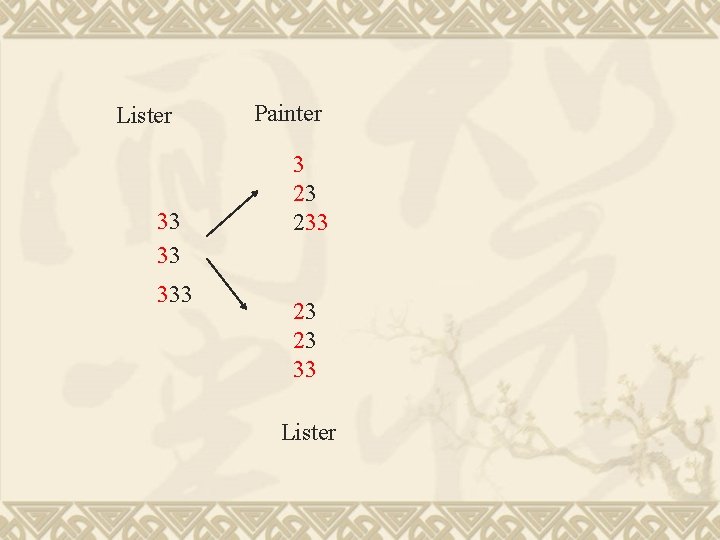
Lister 33 33 333

Lister 33 33 333 Painter 3 23 23 33

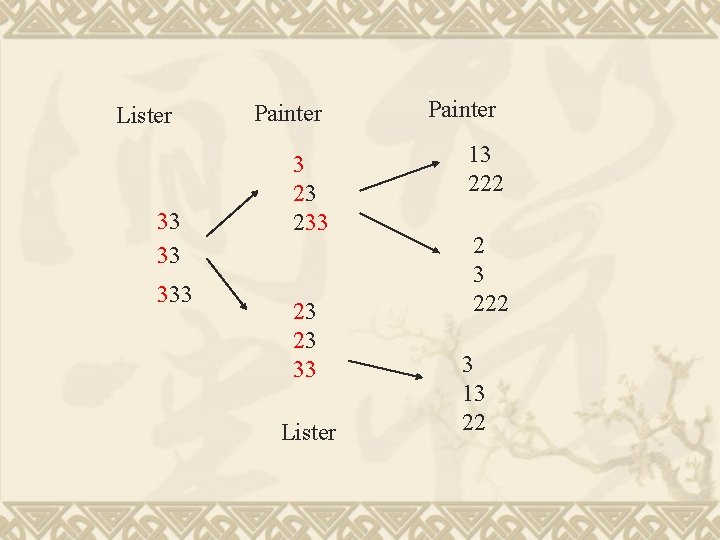
Lister 33 33 333 Painter 3 23 23 33 Lister

Lister 33 33 333 Painter 3 23 23 33 Lister

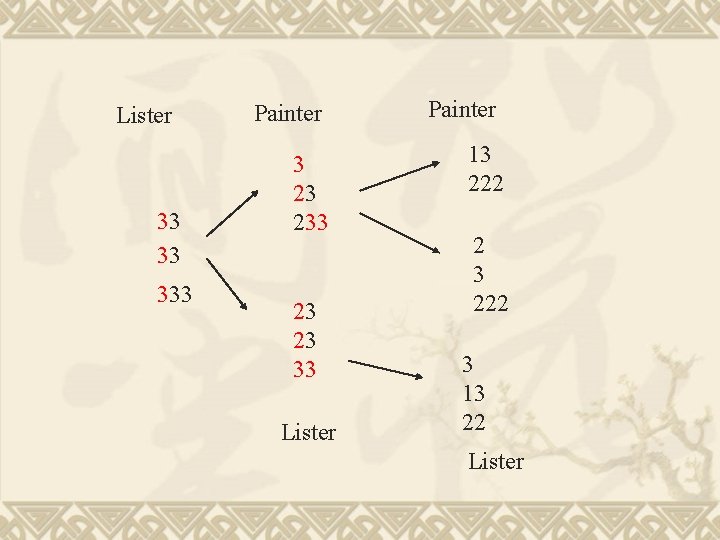
Lister 33 33 333 Painter 3 23 23 33 Lister Painter 13 222 2 3 222 3 13 22

Lister 33 33 333 Painter 3 23 23 33 Lister Painter 13 222 2 3 222 3 13 22 Lister

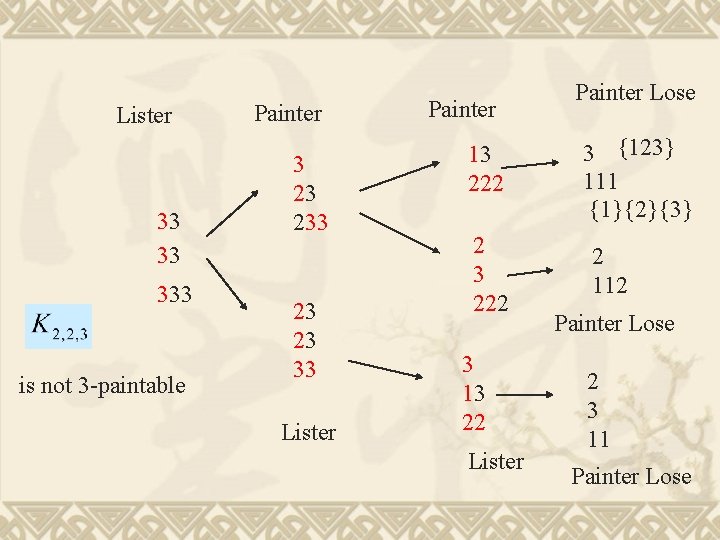
Lister 33 33 333 is not 3 -paintable Painter 3 23 23 33 Lister Painter 13 222 2 3 222 3 13 22 Lister Painter Lose 3 {123} 111 {1}{2}{3} 2 112 Painter Lose 2 3 11 Painter Lose

Theorem [Huang-Wong-Zhu, 2011] is k-paintable = deg(P(G))

Theorem [Huang-Wong-Zhu, 2011] is k-paintable

Theorem [Mahoney, Tomlinson Wise, 2014] If G is an outerplanar graph whose weak dual is a path, then G is online sum choice greedy. Conjecture [Mahoney, Tolinson, Wise] Every outerplanar graph is online sum choice greedy.