OLIMPIADA MATEMTICA 2009 FASE autonmica SEGON CICLE PROVA

OLIMPIADA MATEMÀTICA 2009 FASE autonómica SEGON CICLE PROVA INDIVIDUAL BENICARLÓ, 6, 7 DE JUNY

1. - Es considera un quadrat ABCD de costat 1. Siga P un punt del costat CB tal que la distància de P a B és ½, d(P, B) = ½ ; i Q un altre punt de CB tal que la distància de Q a B és 1/3, d(Q, B) = 1/3. Proveu que és verifica BAC = BAP + BAQ. SOLUCIÓ: Proporcionarem quatre solucions SOLUCIÓ 1: Dibuix amb regla i compàs, comprovant la suma d’angles amb el compàs SOLUCIÓ 2: Utilizant raons trigonomètriques, per example la tangent i calculadora

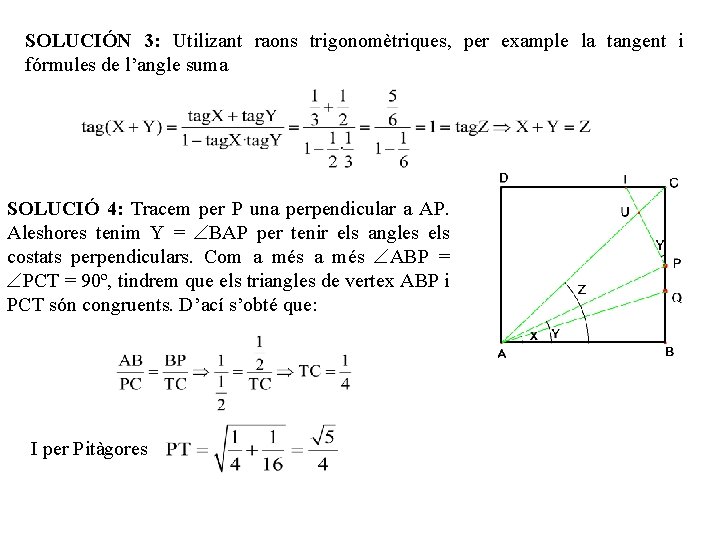
SOLUCIÓN 3: Utilizant raons trigonomètriques, per example la tangent i fórmules de l’angle suma SOLUCIÓ 4: Tracem per P una perpendicular a AP. Aleshores tenim Y = BAP per tenir els angles els costats perpendiculars. Com a més ABP = PCT = 90º, tindrem que els triangles de vertex ABP i PCT són congruents. D’ací s’obté que: I per Pitàgores

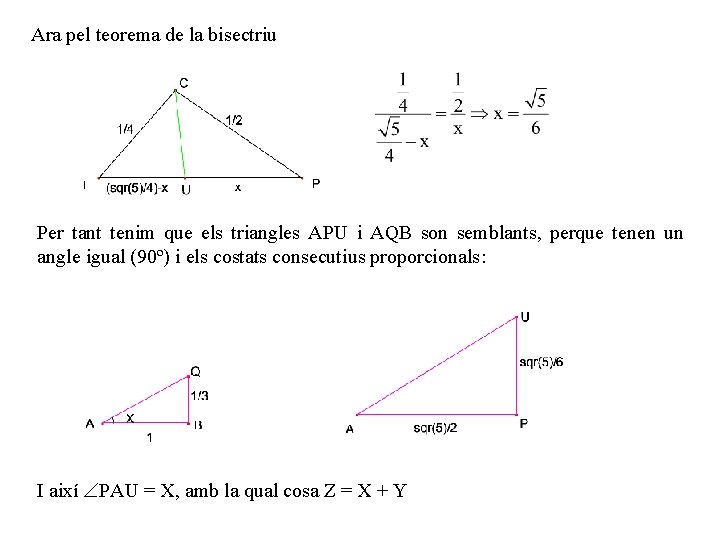
Ara pel teorema de la bisectriu Per tant tenim que els triangles APU i AQB son semblants, perque tenen un angle igual (90º) i els costats consecutius proporcionals: I així PAU = X, amb la qual cosa Z = X + Y

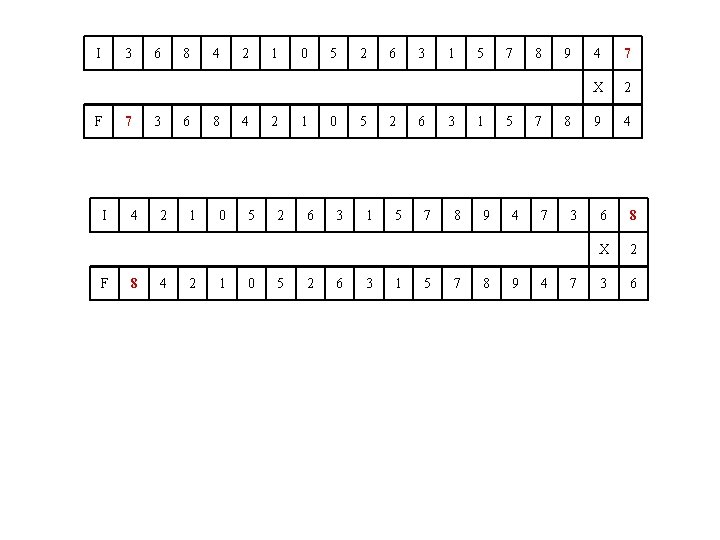
2. - Un grup d’alumnes no té professor, i aprofitant el moment un de tants escriu a la pisarra un número molt llarg, de 18 xifres. Quan arriba el professor de guàrdia, esborra l’última xifra de la dreta i l’escriu al començáment, quedant així un número amb doble valor que el que hi havia inicialment. Quin número havia escrit l’alumne a la pisarra? SOLUCIÓ: Siga I el número inicial i F el final. Tenim A més a més la xifra de les unitats, decenes, centenes, . . . de F és la xifra de les decenes, centenes, unitats de miler, . . . de I. I que F = 2·I. Si suposem que a = 1, tenim I F 3 7 6 3 8 6 4 8 2 1 X 2 4 2

I així plegariem a: I F 3 7 6 3 8 6 4 8 2 4 1 2 0 1 7 5 8 7 9 8 4 9 7 4 3 7 6 3 8 6 4 8 2 1 X 2 4 2 Per tant a no pot ser 1, perque la xifra inicial de I no és la final de F. Analogament a no pot ser 0, 2, 3, 6, 9. Per als casos a = 4, 5, 7, 8 eixen les posibles solucions del problema I 2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 X 2 F 4 2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 I 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2 1 0 5 X 2 1 0 F 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2

I 3 F I F 7 4 8 6 3 2 4 8 6 1 2 4 8 0 1 2 4 5 0 1 2 2 5 0 1 6 2 5 0 3 6 2 5 1 3 6 7 5 1 3 8 7 5 1 9 8 7 5 4 9 8 7 7 4 9 8 3 7 4 7 X 2 9 4 6 8 X 2 3 6

3. - Dos comerciants de vi van entrar en Paris amb 64 i 20 barrils de vi respectivament. Com que no tenien prou per pagar els drets de duana, el primer d’ells va entregar 5 barrils i 40 francs, mentre que el segon va donar 2 barrils, rebent 40 francs com a camvi. Quin era el preu de cada barril i el seu impost duaner? SOLUCIÓ: Un problema d’enunciat: Planteja una situació real i pregunta pel valor de algunes coses. Si x = preu del barril i y = impost duaner, tenim: Aïllant x en la primera i segona equació e igualant Per tant el preu de cada barril es 120 francs i el impost duaner es de 1/12 francs

4. - En el sorteig de la Loteria Primitiva s’extrauen 6 boles de 49 números possibles, amés d’una altra bola amb els número complementari i una bola d’un altre bombo (del 0 al 9) per a determinar el reintegrament (devolució de la’aposta). Hi ha un primer premi “gros” per als encertants del sis números de la combinació guanyadora; i uns altres premis menors: cinc números mes el complementari, cinc números, quatre números, tres números i el reintegrament. El preu de l’aposta es un euro. Si apostem un euro, calculeu la probabilitat de que toque cadascun dels premis. Solució: Escollim sis caselles de les 49 possibles. Per tant la probabilitat d’encertar el sis números és: La probabilitat d’encertar-ne cinc i fallar-ne un, és, degut a que el fallat pot estar en qualsevol de les sis posicions:

La probabilitat d’encertar cinc números més el complementari és la probabilitat d’encertar-ne cinc i fallar-ne un (és a dir la calculada abans) i encertar el complementari, per tant és: La probabilitat d’encertar-ne quatre i fallar-ne dos és, degut a que els dos fallats poden estar en qualsevol de les sis posicions La probabilitat d’encertar-ne tres i fallar-ne tres és, degut a que els tres fallats poden estar en qualsevol de les sis posicions La probabilitat de que ens tornen l’aposta és:

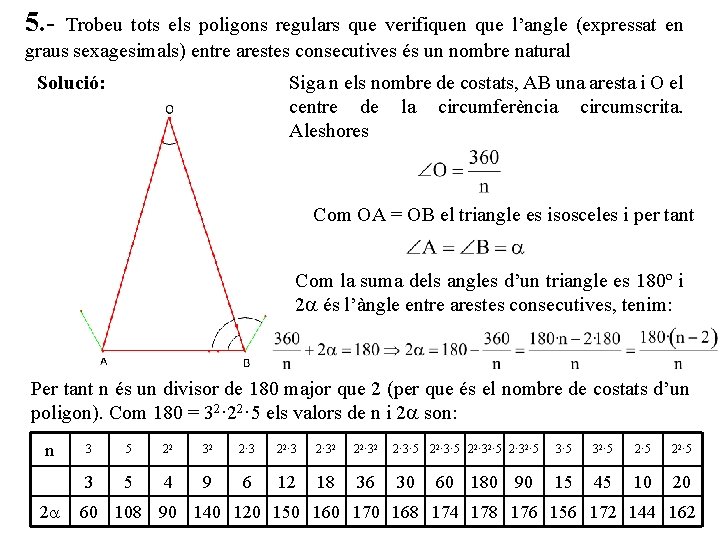
5. - Trobeu tots els poligons regulars que verifiquen que l’angle (expressat en graus sexagesimals) entre arestes consecutives és un nombre natural Solució: Siga n els nombre de costats, AB una aresta i O el centre de la circumferència circumscrita. Aleshores Com OA = OB el triangle es isosceles i per tant Com la suma dels angles d’un triangle es 180º i 2 és l’àngle entre arestes consecutives, tenim: Per tant n és un divisor de 180 major que 2 (per que és el nombre de costats d’un poligon). Com 180 = 32· 22· 5 els valors de n i 2 son: n 2 3 5 22 32 2· 32 22· 32 3 5 4 9 6 12 18 36 2· 3· 5 22· 32· 5 30 60 180 90 3· 5 32· 5 22· 5 15 45 10 20 60 108 90 140 120 150 160 170 168 174 178 176 156 172 144 162