OLIMPIADA MATEMTICA 2010 FASE PROVINCIAL PRIMRIA PROVA INDIVIDUAL

OLIMPIADA MATEMÀTICA 2010 FASE PROVINCIAL PRIMÀRIA PROVA INDIVIDUAL CASTELLÓ (UJI), 15 DE MAIG DE 2010

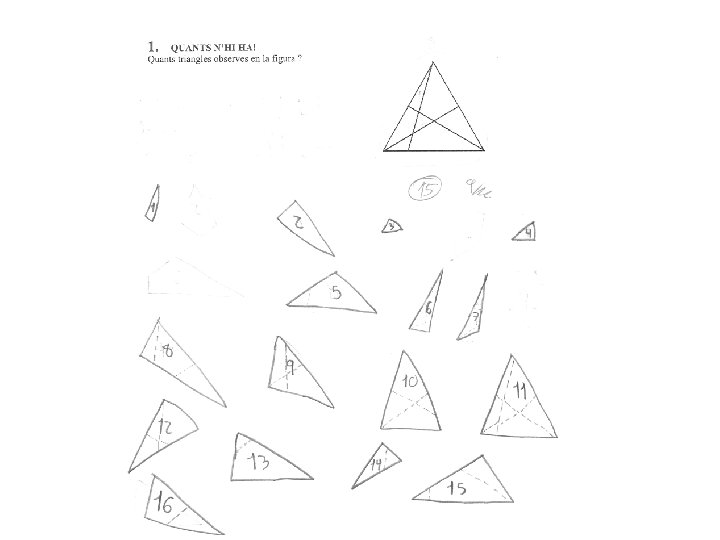
1. - QUANTS HI HA. - Quants triangles observes en la figura?

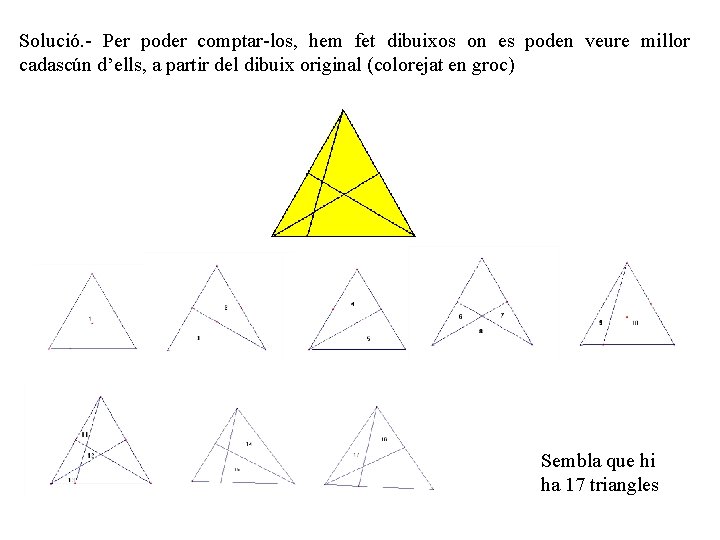
Solució. - Per poder comptar-los, hem fet dibuixos on es poden veure millor cadascún d’ells, a partir del dibuix original (colorejat en groc) Sembla que hi ha 17 triangles

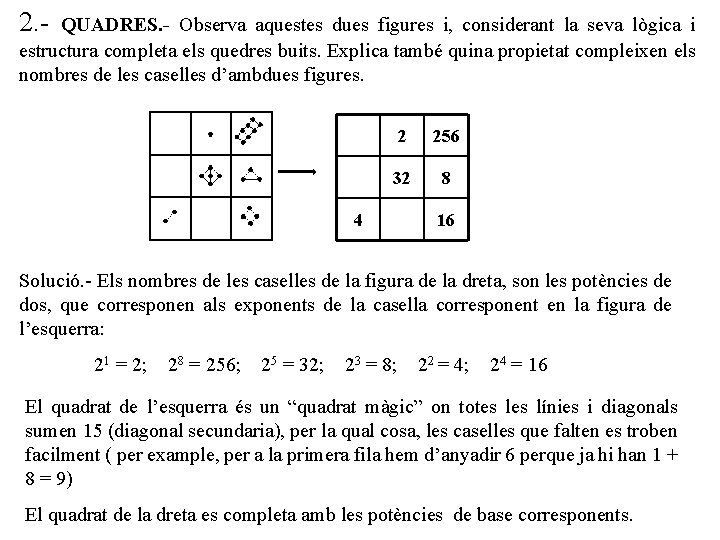
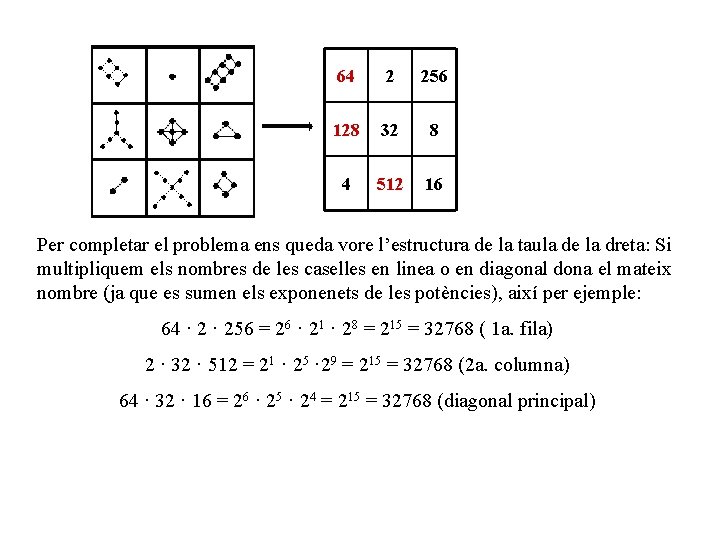
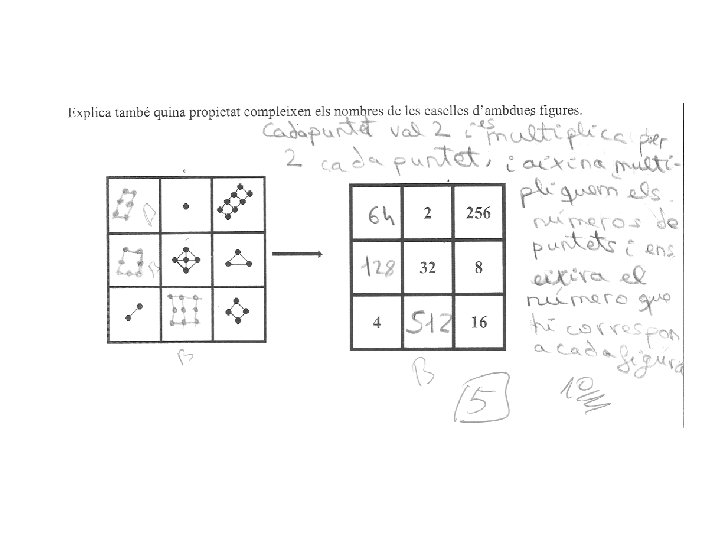
2. - QUADRES. - Observa aquestes dues figures i, considerant la seva lògica i estructura completa els quedres buits. Explica també quina propietat compleixen els nombres de les caselles d’ambdues figures. 2 256 32 8 4 16 Solució. - Els nombres de les caselles de la figura de la dreta, son les potències de dos, que corresponen als exponents de la casella corresponent en la figura de l’esquerra: 21 = 2; 28 = 256; 25 = 32; 23 = 8; 22 = 4; 24 = 16 El quadrat de l’esquerra és un “quadrat màgic” on totes línies i diagonals sumen 15 (diagonal secundaria), per la qual cosa, les caselles que falten es troben facilment ( per example, per a la primera fila hem d’anyadir 6 perque ja hi han 1 + 8 = 9) El quadrat de la dreta es completa amb les potències de base corresponents.

64 2 256 128 32 8 4 512 16 Per completar el problema ens queda vore l’estructura de la taula de la dreta: Si multipliquem els nombres de les caselles en linea o en diagonal dona el mateix nombre (ja que es sumen els exponenets de les potències), així per ejemple: 64 · 256 = 26 · 21 · 28 = 215 = 32768 ( 1 a. fila) 2 · 32 · 512 = 21 · 25 · 29 = 215 = 32768 (2 a. columna) 64 · 32 · 16 = 26 · 25 · 24 = 215 = 32768 (diagonal principal)

3. - UNA GALLINA, QUATRE GALLINES. . . - Una gallina pon dos ous cada tres dies. Quants dies es necessitaran perqué quatre gallines ponguen dues dotzenes d’ous? Solució. - Es tracta d’un problema de proporcionalitat: hi han tres magnituts: nombre de gallines, nombre d’ous, nombre de dies relacionades proporcionalment entre eeles ( al multiplicar un valor d’una d’elles per un factor l’altra magnitud queda multiplicada per el mateix factor, per example, el triple de gallines pondran el triple d’ous, si esperem el doble de dies pondran el doble d’ous). Per contestar la pregunta de l’enunciat poden seguir diverses tàctiques: (A). - Una gallina pon per dia, per tant 4 gallines pondran Com volem saber quants dies son necessaris per a que 4 gallines ponguen 24 ous, caldrá dividir el nombre d’ous a pondre per la “velocitat de posta” de les quatre gallines

(B). - Utilitzant aquest esquema: nombre de gallines 1 gallina x 4 4 gallines nombre d’ous nombre de dies 2 ous 3 dies x 4 8 ous 3 dies x 3 24 ous 9 dies

4. - LA SERP SÚMICA. - Situa en els cercles de la serp els nombres de l’ 1 al 9, de manera que cada linea de tres nombres sume 13 Solució: Despres de fer alguns intents fallits com 2 8 3 1 6 4 7 5 6 7 2 2 8 3 9 1 nos en adonem que són importants els nombres que col·loquem en els vértexs de la serp (en roig en els casos anteriors) perqué són sumats dos vegades i perqué han de ser els nombres que més vegades facen apareixer suma 13

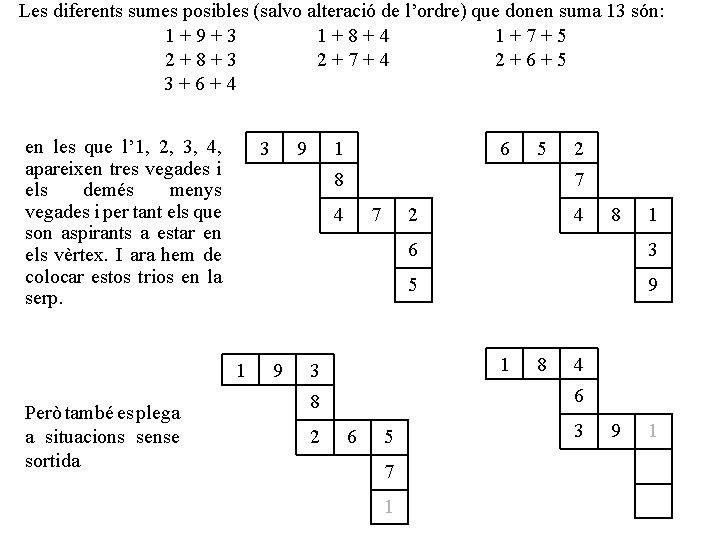
Les diferents sumes posibles (salvo alteració de l’ordre) que donen suma 13 són: 1+9+3 1+8+4 1+7+5 2+8+3 2+7+4 2+6+5 3+6+4 en les que l’ 1, 2, 3, 4, apareixen tres vegades i els demés menys vegades i per tant els que son aspirants a estar en els vèrtex. I ara hem de colocar estos trios en la serp. 3 1 6 5 8 9 7 2 4 8 1 6 3 5 9 1 3 8 4 6 8 2 2 7 4 1 Però també es plega a situacions sense sortida 9 6 5 7 1 3 9 1

5. - EDAT. - A un aficionat a les andivinalles li van preguntar quina era la seva edat. La resposta, com era d’esperar, va sert una endevinalla: “Si multipliques per tres l’edat que tindré d’ací a tres anys i li restes el triple de l’edat que tenia fa tres anys obtindràs le meva edat” Quina es la seva edat? Solució: La resposta la podem obtenir per assaig i errada: Partim d’un nombre qualsevol i cal comprovar si compleix l’enunciat del problema. per tant 20 no es l’edat de la persona. Provem un altre nombre:

per tant 17 no es l’edat de la persona. Provem un altre nombre: Per tant la persona té 18 anys. Per als adelantats: L’enunciat es pot passar a expressión algebraiques com: on x és l’edat. Resolguen l’equació, resulta: