Modified error estimates for discrete variational derivative methods

Modified error estimates for discrete variational derivative methods Chris Budd (Bath), Takaharu Yaguchi (Tokyo), Daisuke Furihata (Osaka)

Have a PDE with solution u(x, y, t) Seek to derive numerical methods which respect/inherit qualitative features of the PDE and to analyse them in this context. Variational structure Gradient structure (dissipation) Conservation laws

Cannot usually preserve all of the structure and Have to make choices Talk will describe the Discrete Variational Derivative Method which works well for PDEs with localised solutions and exploits variational structures 1. Will show the method works 2. Will analyse using modified equation analysis 3. Will derive modified conservation laws and a modified variational structure 4. Deduce the existence of soliton solutions

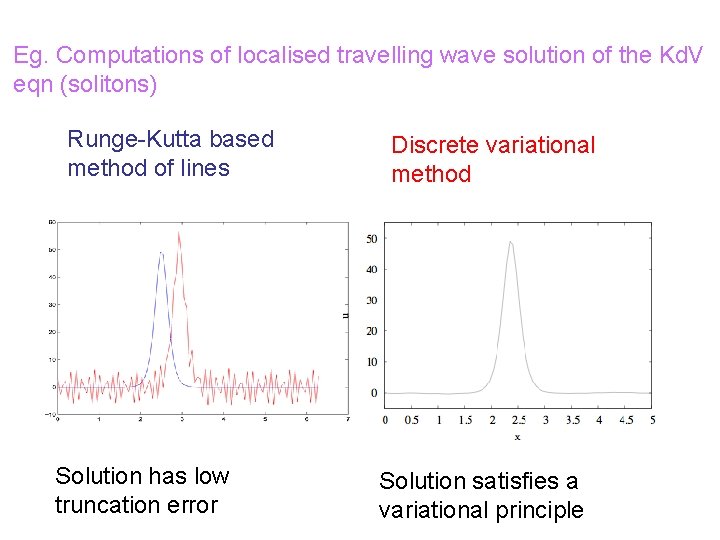
Eg. Computations of localised travelling wave solution of the Kd. V eqn (solitons) Runge-Kutta based method of lines Solution has low truncation error Discrete variational method Solution satisfies a variational principle

1. Look at PDEs with a (gradient) Variational Structure. Definition, let u be defined on the interval [a, b]

PDE has a Variational Form if Example 1: Heat equation Example 2: Heat equation (again)

Example 3: Kd. V Equation Example 4: Cahn Hilliard Equation

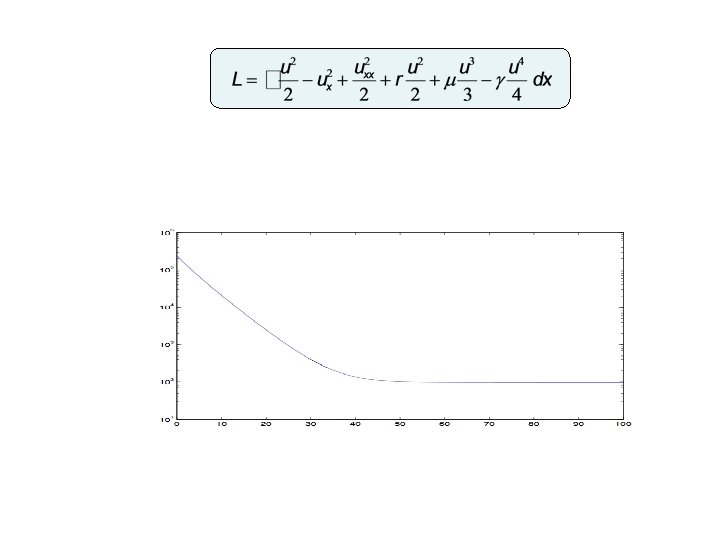
Example 5: Swift-Hohenberg Equation Integral of G is the Lagrangian L.

Variational structure is associated with dissipation or conservation laws: Theorem 1: If Proof:

2. Discrete Variational Derivative Method (DVDM) [B, Furihata, Ide, Matsuo, Yaguchi] (closely related to Discrete Gradient Methods [Owren, Celledoni, Quispel]) Aim to reproduce this structure for a discrete system Advantages: Modified dissipation and conservation laws Idea: Discrete ‘energy’ Discrete integral and discrete integration by parts

Define: Where the integral is replaced by the trapezium rule Note: This is exact for band limited periodic functions Now define the Discrete Variational Derivative by: Discrete Variational Derivative Method

Some useful results Definitions Summation by parts

Generally [Furihata], if

Example 1: Heat equation F(u)=0: Crank-Nicholson Method

More generally, if Set Eg. Kd. V

Conservation/Dissipation Property A key feature of DVDM schemes is that they inherit the conservation/dissipation properties of the PDE and hence have nice stability properties Theorem 2: For any N periodic sequence satisfying DVDM Proof. by the summation by parts formulae

Example 2: Nonlinear heat equation Implementation : Can prove this has a solution if time step small enough: choose this adaptively • Predict solution at next time step using a standard implicitexplicit method • Correct using a Powell Hybrid solver

Example 3: Swift-Hohenberg Equation

3. Modified Equation Error Analysis This gives some further insight into the solution behaviour Idea: Set Find a suitable function and ‘nice’ operator A: Deduce associated conservation/dissipation laws First consider semi-discrete form then fully discrete

Example of the heat equation: Derived scheme This can be considered to be given by applying the Averaging Vector Field (AVF) method to the ODE system Consider differentiable function Periodic on Fourier transform

Invert to give Modified equation G: Fejer Kernel: Finite support, positive, symmetric, continuous triangular function

Properties of the A operator • Smoothing operator • Positive semi-definite • Symmetric • Commutes with derivative operators • Has a positive square-root H: Rectangular function

Variational Structure The modified equation has various variational structures, each of which leads to a dissipation property.

Generalisations to other PDEs Let be the nth finite difference operator. Define the smoothing operator by rescaled Is a convolution operator

Some useful results: Let u(x) be periodic on , T the trapezoidal sum: (A) (B)

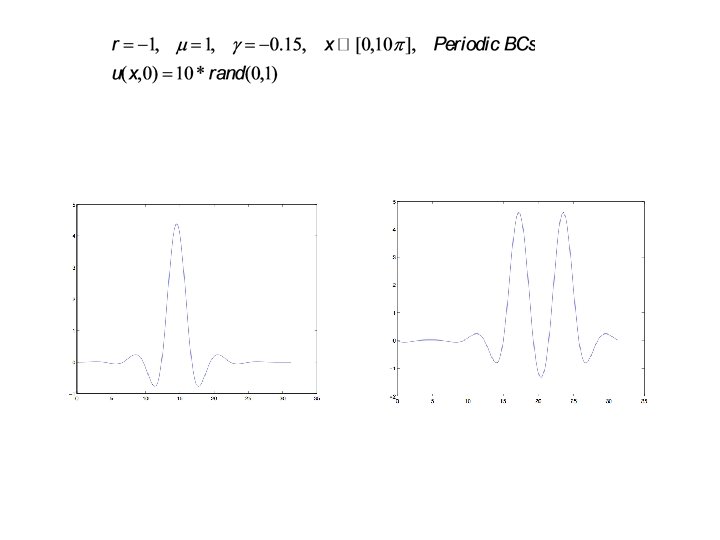
Applications Example 1: Nonlinear conservation laws Periodic boundary conditions on Exact conserved quantities:

DVDM method has the semi-discrete modified equation Lemma 1: Proof: The following are conserved

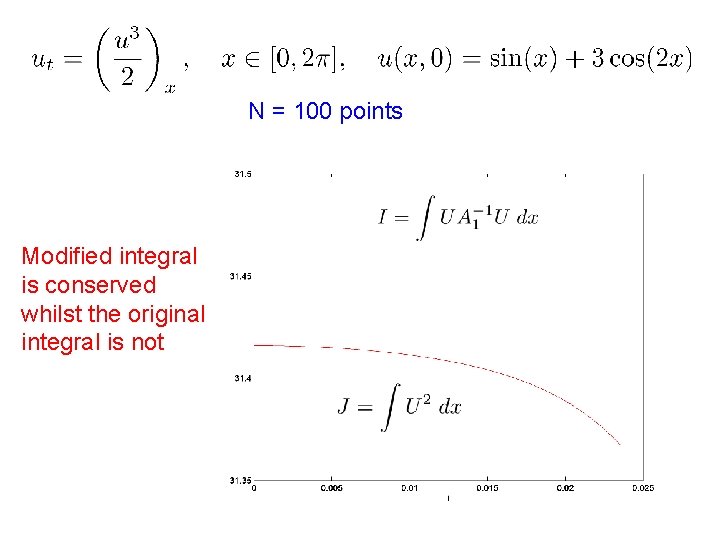
The conservation of is more subtle We introduce a modified square norm Lemma 2. If u(x, 0) is band limited, then I(U) is conserved

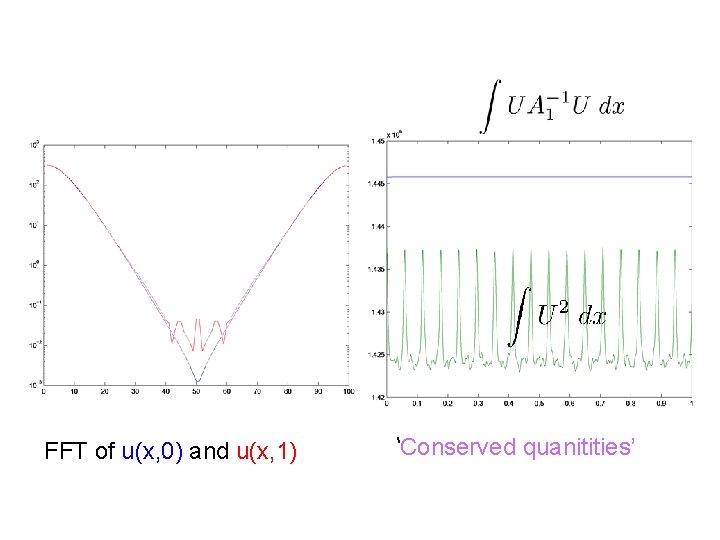
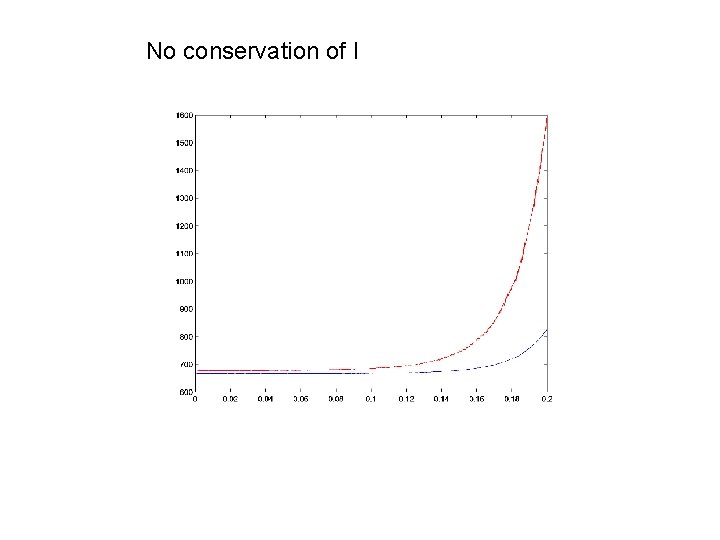
N = 100 points Modified integral is conserved whilst the original integral is not

Example 2: Fourth order dissipative problem Modified equation Positive definite smoothing operator. This implies

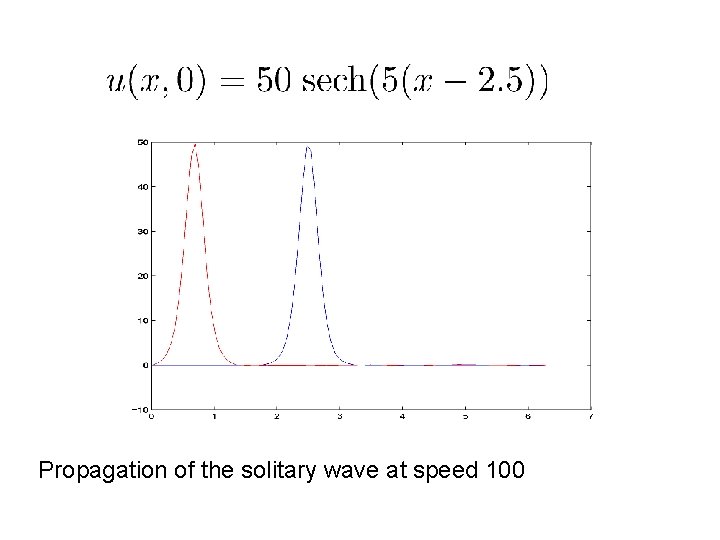
Example 3: The Kd. V equation The DVDM method leads to the full discretisation With the semi-discretisation

The modified equation has the form: Note the action of the smoothing operators It has the variational structure:

Conservation Laws It is immediate that TU and TG are conserved. As before, if u(x, 0) is band limited then is conserved The band limitation of U follows from the action of the smoothing operators.

Propagation of the solitary wave at speed 100

FFT of u(x, 0) and u(x, 1) ‘Conserved quanitities’

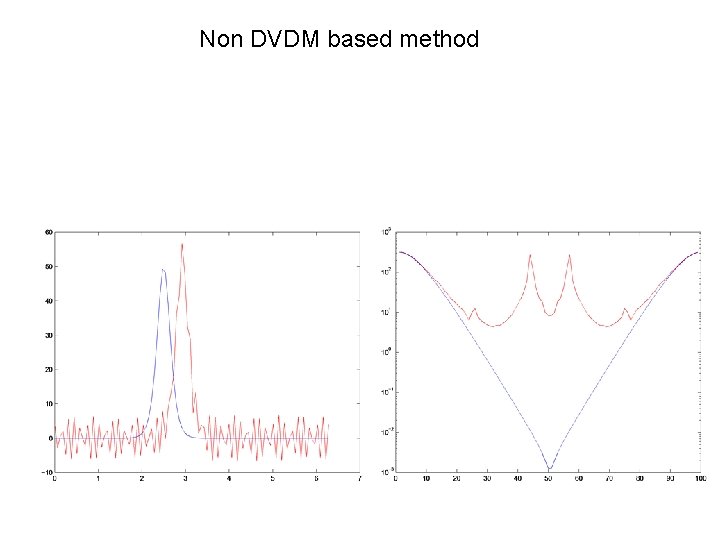
Non DVDM based method

No conservation of I

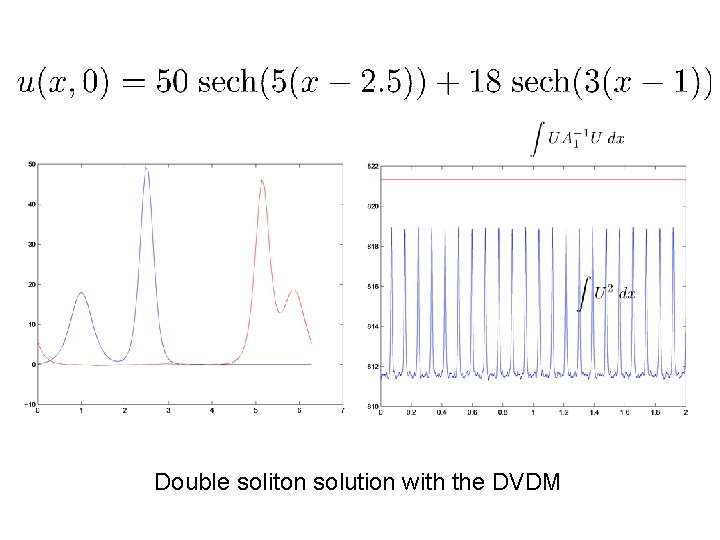
Double soliton solution with the DVDM

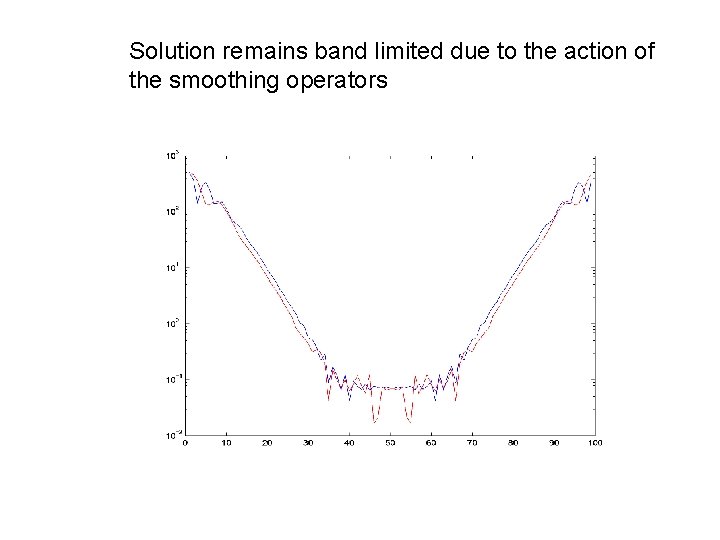
Solution remains band limited due to the action of the smoothing operators

Existence of soliton solutions This follows directly from a variational problem which is a modified version of a problem considered by [Benjamin] Subject to This has a minimiser

The minimiser satisfies the ordinary differential eqn Now set Giving Hence the modified eqn admits a travelling wave solution

Conclusions • Discrete Variational Derivative Method gives a systematic way to discretise PDEs in a manner which preserves useful qualitative structures • Modified Equation Analysis helps to determine these structures • Allowing us to deduce (modified) conservation laws and the existence of soliton solutions • Method can be extended (with effort) to higher dimensions and irregular meshes • Natural way to work with PDEs with a variational structure