MODELOWANIE ZMIENNOCI CEN AKCJI MODEL ADDYTYWNY MODEL MULTIPLIKATYWNY

MODELOWANIE ZMIENNOŚCI CEN AKCJI MODEL ADDYTYWNY MODEL MULTIPLIKATYWNY

Modele zmienności aktywów z czasem dyskretnym / Model addytywny Przyjmijmy następujące oznaczenia: S(0) - cena początkowa akcji S(k) - cena akcji w k-tym etapie u(k) , k= 0, 1, 2, …n ciąg niezależnych zmiennych losowych o jednakowej wartości oczekiwanej μ oraz o tej samej wariancji równej σ2. Będziemy go interpretować jako losowe fluktuacje.

Model addytywny Rozważmy model ceny aktywu postaci (1) S(k+1) = a S(k) + u (k) Gdzie u(k) – losowe fluktuacje, k=0, 1, 2, . . . zaś a jest pewną dodatnią liczbą rzeczywistą, decydującą o trendzie głównym. Dla a > 1 trend główny jest wzrostowy. Znając wartości u(0), . . . , u(n) można wyznaczyć S(1), S(2), …, S(n). W tym modelu cena akcji w dowolnym momencie zależy wyłącznie od ceny w momencie go poprzedzającym i od losowej fluktuacji.

Model addytywny Ze wzoru (1) otrzymujemy S(1) = a. S(0) + u(0) , S(2) = a. S(1) + u(1) = a[a. S(0) + u(0)] + u(1)= = a 2 S(0) + au(0) + u(1) S(3) = a. S(2)+u(2) = a [a 2 S(0) + au(0) + u(1)] +u(2)= = a 3 S(0) + a 2 u(0) + au(1) + u(2) Uwaga 1. Dla dowolnego k cena S(k) dana jest wzorem: (2) S(k) = ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+a u(k-2) + u(k-1).

Model addytywny Rzeczywiście, dla k = 1 wzór jest prawdziwy (z definicji modelu). Zakładając prawdziwość dla k, z ciągu równości : S(k+1) = a S(k) + u (k)= a[ak. S(0) + ak-1 u(0) + ak-2 u(1) +… +a u(k-2) + u(k-1)] + u (k)= = ak+1 S(0) + aku(0) + ak-1 u(1) +…+a 2 u(k-2) + au(k-1) + u (k) oraz indukcji matematycznej wynika prawdziwość wzoru (2)

Model addytywny. Wartość oczekiwana zmiennej S(k). Z elementarnych własności wartości oczekiwanej oraz z założenia E[u(k)] = μ dla każdego k mamy E[S(k)] = E( ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+ au(k-2) + u(k-1))= = ak. E[S(0)] + ak-1 E[u(0)] + ak-2 E[u(1)] +…+a. E[u(k-2)]+E[u(k-1)] = ak. S(0) + ak-1 μ + ak-2 μ +…+a μ + μ E[S(k)] = ak. S(0) + μ(1 -ak)/(1 -a), o ile a jest różne od 1 albo E[S(k)] = S(0) + k μ, gdy a = 1

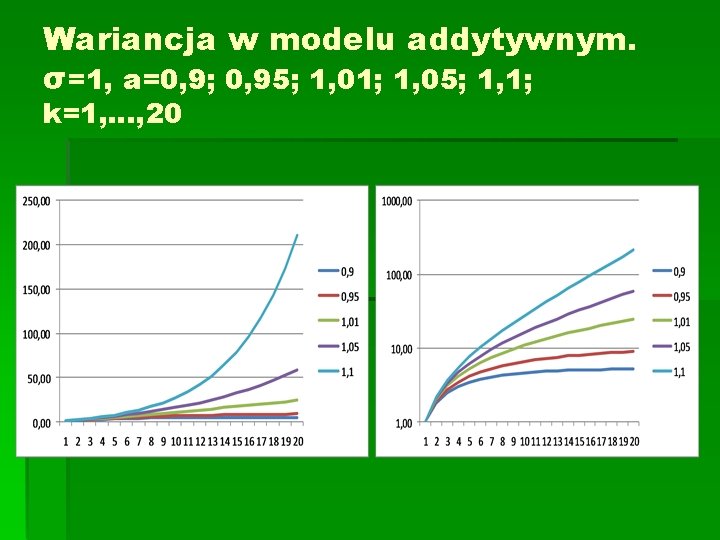
Model addytywny. Wariancja ceny Korzystając z podstawowych własności wariancji oraz założenia niezależności zmiennych losowych otrzymujemy Var [S(k)] = Var [ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+ u(k-1)] = = Var [ak-1 u(0)] + Var[ak-2 u(1)] +…+Var[u(k-1)] = = (ak-1)2 Var [u(0)]+ (ak-2)2 Var [u(1)]+…+ a 2 Var [u(k-2)] + +Var [u(k)] = = a 2(k-1)σ2+ a 2(k-2)σ2 +…+a 2σ2 +σ2 = = (1+a 2+a 4+…+a 2 k-2) σ2 = σ2(1 - a 2 k) / (1 - a 2), gdy a różne od 1 Var [S(k)] = k σ2, dla a = 1

Wariancja w modelu addytywnym. σ=1, a=0, 9; 0, 95; 1, 01; 1, 05; 1, 1; k=1, …, 20

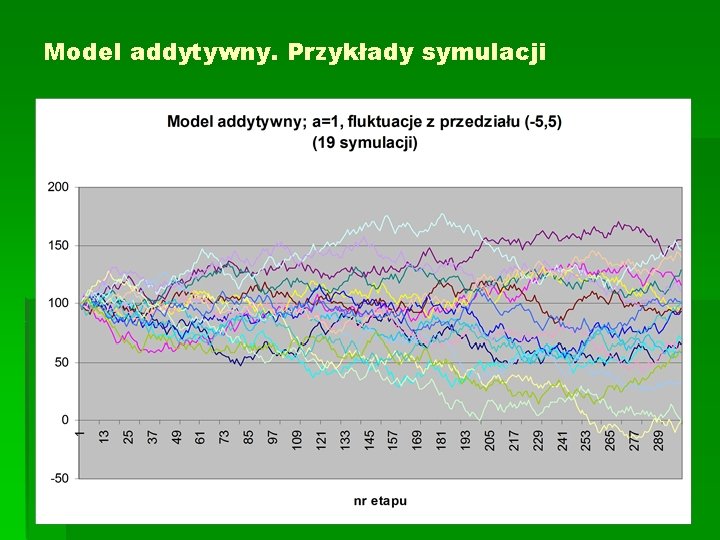
Model addytywny. Przykład Rozważmy 300 – etapową symulację w modelu addytywnym. Cena początkowa akcji: 100 zł, a =1, fluktuacje w każdym etapie są liczbami losowymi z przedziału (-5 zł, 5 zł).

Model addytywny. Przykłady symulacji

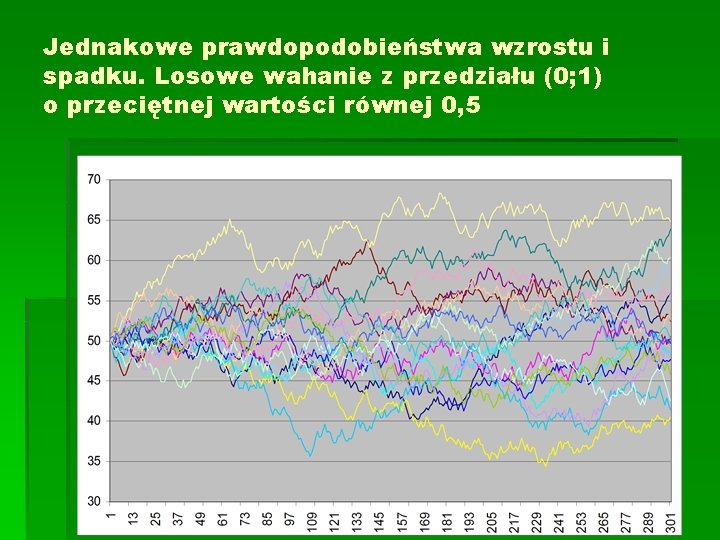
Jednakowe prawdopodobieństwa wzrostu i spadku. Losowe wahanie z przedziału (0; 1) o przeciętnej wartości równej 0, 5

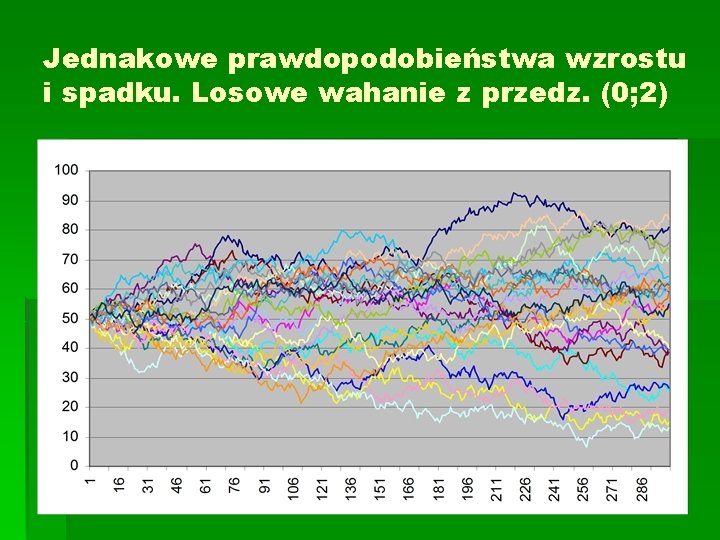
Jednakowe prawdopodobieństwa wzrostu i spadku. Losowe wahanie z przedz. (0; 2)

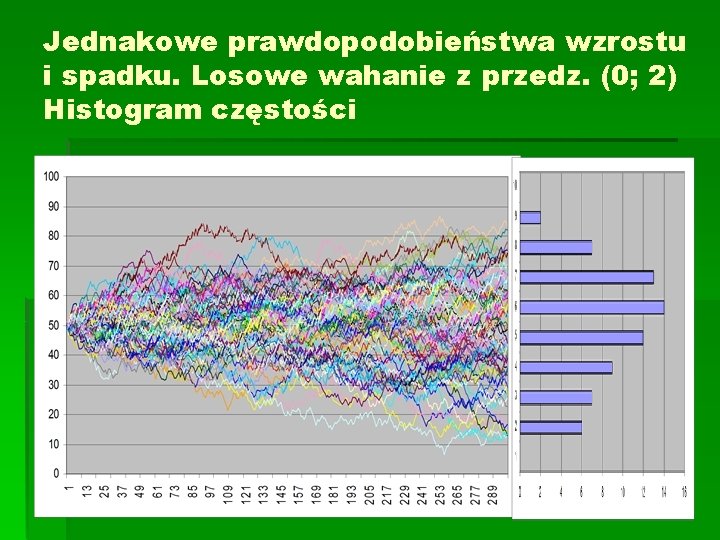
Jednakowe prawdopodobieństwa wzrostu i spadku. Losowe wahanie z przedz. (0; 2) Histogram częstości

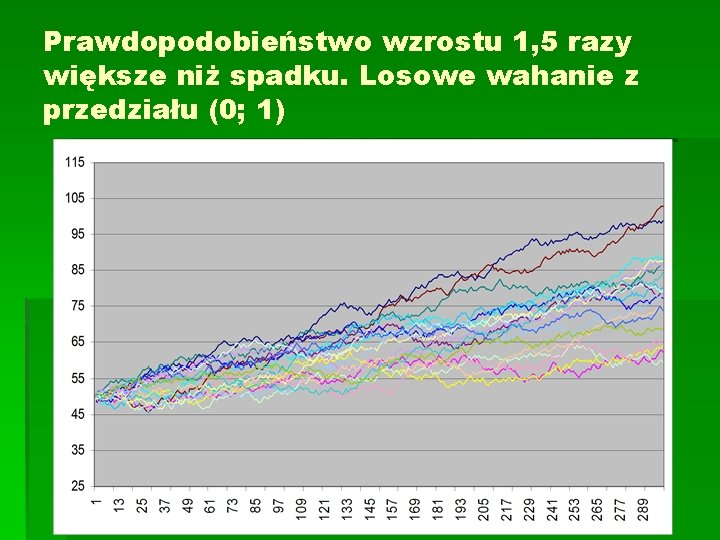
Prawdopodobieństwo wzrostu 1, 5 razy większe niż spadku. Losowe wahanie z przedziału (0; 1)

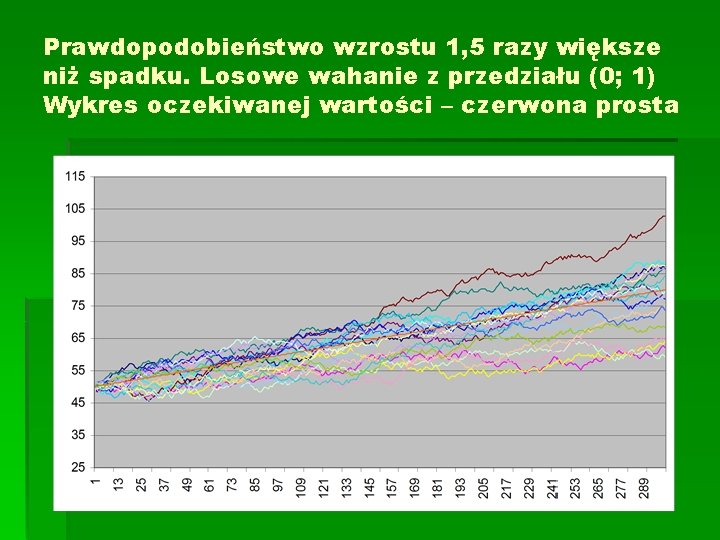
Prawdopodobieństwo wzrostu 1, 5 razy większe niż spadku. Losowe wahanie z przedziału (0; 1) Wykres oczekiwanej wartości – czerwona prosta

Model addytywny (przypadek a=1). Zmienne losowe u(k) o rozkładzie dwupunktowym S(k+1) = S(k) + u (k) u(k) mają rozkład dwupunktowy, k=0, 1, 2, . . . tzn. u(k) = σ lub u(k) = - σ, ( σ > 0 ) z jednakowymi prawdopodobieństwami S(n) = S(0) + u (1) +…+ u (n-1) Sn= u (0) + u (1) +…+ u (n-1) S(n) = S(0) + Sn Sn wyraża zmianę ceny po n etapach Wtedy: E[u (i)] = 0 Var [u (i)] = 0, 5(σ-0)2 + 0, 5(-σ-0)2 = σ2 E[Sn]= 0 Var Sn = Ʃni=1 Var [u (i)] = n σ2 Wzór na wariancję wynika z niezależności ciągu zmiennych losowych (u(i)). Z elementarnych własności wartości oczekiwanej i wariancji otrzymujemy E[S(n)]= S(0) Var S(n) = n σ2 Oznaczając przez σn odchylenie standardowe zmiennej Sn, mamy σn = σ n

Centralne twierdzenie graniczne Standaryzacja zmiennej losowej Sn § S*n = (Sn-E(Sn))/σn Uwzględniając poprzednie wyliczenia § S*n= Sn/ σ n § TW (CTG) Niech (Xn) będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach (niekoniecznie dwupunktowych) oraz E Xi = μi, Var Xi = σ2 dla i=1, …, n. Sn = X 1 + X 2 +… + Xn. Wtedy § (8) § (9) §

W przypadku m = 0 mamy W szczególności

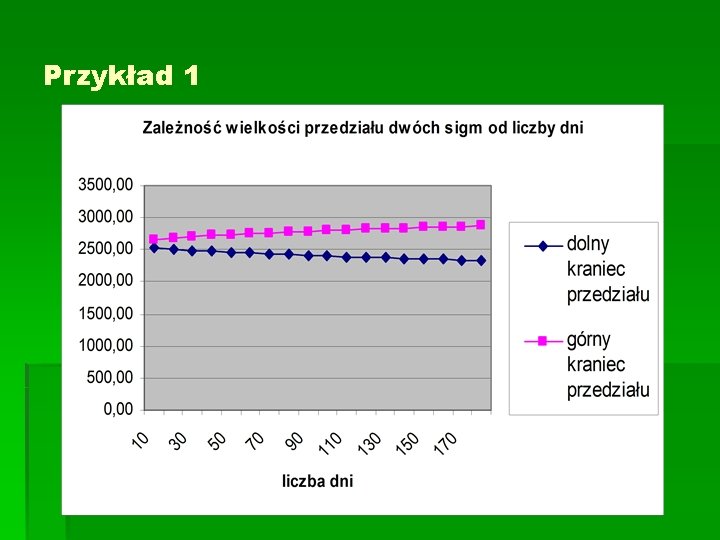
Przykład 1 § Kurs kontraktu futures na WIG 20 ma 2600 pt. Zakładamy, że każdego dnia kurs ma taką samą szansę na wzrost co na spadek o 10 punktów. W jakim przedziale znajdzie się z prawdopodobieństwem 0, 9545 kurs tego kontraktu po 30 dniach ? , (po 50? , po 100 ? ) § Zastosujemy centralne twierdzenie graniczne a w szczególności wykorzystamy przybliżenie § Ponieważ σ = 10, n=30 mamy więc § Otrzymaliśmy przedział na zmianę ceny, zatem uwzględniając S(n) = S(0) + Sn mamy §

Przykład 1 § Dla 50 i 100 dni mamy odpowiednio

Przykład 1

Model addytywny. Uwagi Mimo swej prostoty i łatwości stosowania model addytywny nie zawsze nadaje się do stosowania go w rzeczywistości. Zmienne u(k) mogą przyjmować wartości ujemne, co oznacza, że model dopuszcza ujemne wartości cen akcji, co jest niemożliwe. Model ten nadaje się do analizy w krótkich okresach i stał się podstawą do zbudowania wielu innych modeli.

Model multiplikatywny Rozważmy model zmienności cen aktywów w którym „nowa” cena powstaje ze „starej” przez pomnożenie przez pewien losowy czynnik. (3) S(k+1) = u(k)S(k) dla k = 0, 1, . . . , n – 1. Zakładamy, że dana jest cena początkowa S(0) oraz że zmienne losowe u(k), k = 0, 1, . . . , n - 1, są dodatnie, mają jednakowe wartości oczekiwane oraz jednakowe wariancje.

Model multiplikatywny Logarytmując (3) stronami: ln S(k+l) = ln S(k) + ln u(k) dla k = 1, 2, . . . , n - 1. Uwaga. Uzyskana postać jest jedną z form modelu addytywnego - wartości ln S(k) są modelowane addytywnie ze stałą a = 1 Oznaczmy w(k) = ln u(k) Losowe fluktuacje są naturalnego z u(k). wyrażone w formie logarytmu Załóżmy dalej, że ciąg {w(k)} jest ciągiem niezależnych zmiennych losowych o jednakowych rozkładach. Niech wartość oczekiwana każdej z nich wynosi μ zaś wariancja σ2.

Model multiplikatywny Korzystając z modelu (3) cena aktywa w chwili k dana jest wzorem S(k) = u(k-1)u(k-2)…u(0)S(0). Po zlogarytmowaniu obu stron

Model multiplikatywny Jeśli wszystkie zmienne w(i) mają tę samą wartość oczekiwaną μ i wariancję σ2 oraz są niezależne, to korzystając z własności wartości oczekiwanej i wariancji sumy niezależnych zmiennych losowych możemy zapisać: E [ln S(k)] = ln S(0) + μk Var [ln. S(k)] = k σ2. Łatwo zauważyć, że zarówno wartość oczekiwana jak i wariancja rosną liniowo względem k.

Rozkład logarytmiczno – normalny § Niech Y oznacza zmienną losową o rozkładzie normalnym N(μ, σ). Niech X = e. Y (Y = ln. X) § DEF. Rozkład prawdopodobieństwa zmiennej losowej X nazywamy rozkładem logarytmiczno – normalnym i oznaczamy Λ(μ, σ) § (X jest funkcją wykładniczą zmiennej losowej o rozkładzie normalnym) § FX – dystrybuanta zmiennej X

Rozkład logarytmiczno – normalny § Zatem § Oznaczmy przez (x) gęstość rozkładu zmiennej X

Model multiplikatywny § Jeżeli w(i) są niezależnymi zmiennymi losowymi o rozkładach normalnych i parametrach μ, σ2, to zmienna losowa ln[S(k)/S(0)] ma rozkład normalny o wartości oczekiwanej (kμ) oraz wariancji kσ2 (Wniosek 3, par. 37, S Zubrzycki „Wykł. rach. p-stwa. . ”) Ponadto, jeżeli w(i) są niezależnymi zmiennymi losowymi o dowolnych rozkładach i parametrach μ, σ2 , to ciąg zmiennych losowych ln [S(k)/ S(0)], (k=0, 1, 2, …) po standaryzacji jest zbieżny do rozkładu normalnego, a więc granica ciągu zmiennych S(k)/ S(0) (k=0, 1, 2, …) ma rozkład logarytmiczno - normalny

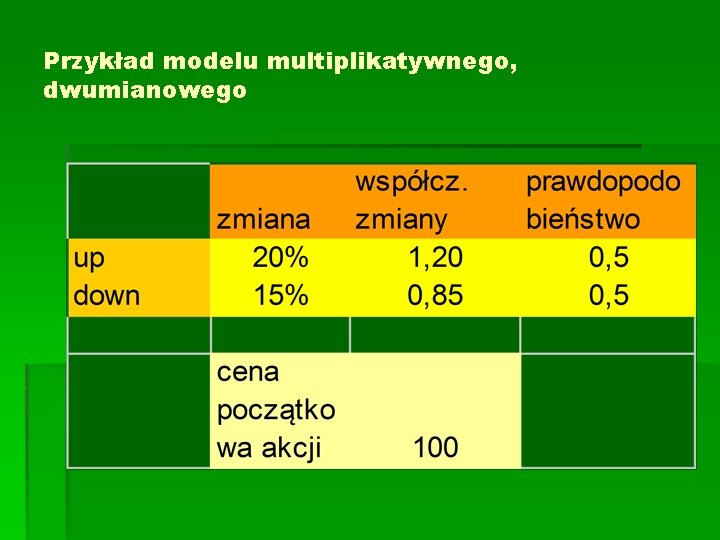
Model multiplikatywny, dwumianowy § Zakładamy, że w każdym okresie cena akcji może obniżyć się lub wzrosnąć, zawsze w tej samej proporcji, czyli przy czym pierwsza z tych wartości jest przyjmowana z prawdopodobieństwem p a druga z (1 -p)

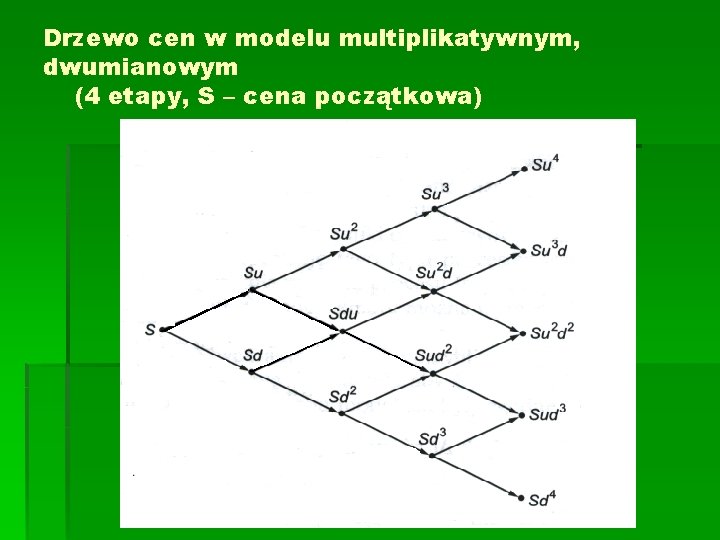
Drzewo cen w modelu multiplikatywnym, dwumianowym (4 etapy, S – cena początkowa)

Ceny końcowe w modelu multiplikatywnym dwumianowym, n-etapowym Ze wzoru (3) wynika, że możliwe ceny końcowe muszą mieć postać S u k d n-k, gdzie k = 0, 1, …, n. Na drzewie cenowym istnieje różnych dróg prowadzących do węzła identyfikowanego z ceną Sukdn-k , gdyż każda droga jest jednoznacznie scharakteryzowana przez n-wyrazowy ciąg (u, u, d, u, …, d, u), zawierający k liter u oraz (n-k) liter d.

Ceny końcowe w modelu multiplikatywnym dwumianowym, n-etapowym § Prawdopodobieństwo każdej takiej drogi – jako koniunkcji zdarzeń niezależnych wynosi § pk (1 -p)n-k Zatem prawdopodobieństwo ceny końcowej Sukdn-k wynosi §

Przykład modelu multiplikatywnego, dwumianowego

Drzewo cen akcji w modelu multiplikatywnym, dwumianowym (10 etapów)

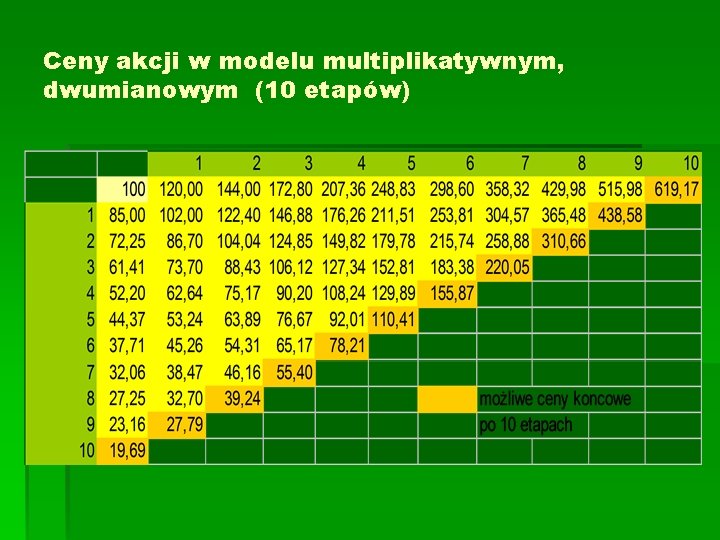
Ceny akcji w modelu multiplikatywnym, dwumianowym (10 etapów)

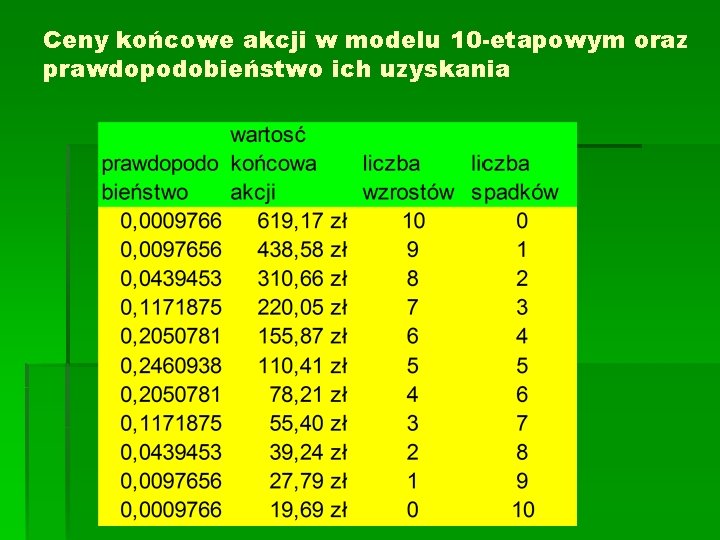
Ceny końcowe akcji w modelu 10 -etapowym oraz prawdopodobieństwo ich uzyskania

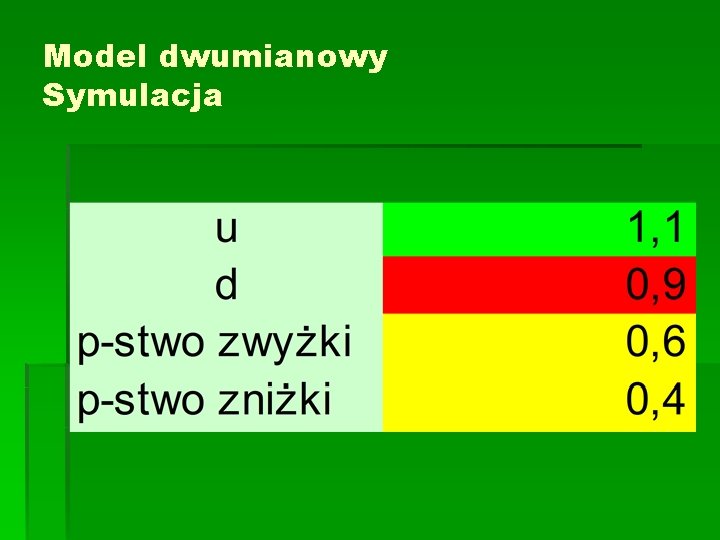
Model dwumianowy Symulacja

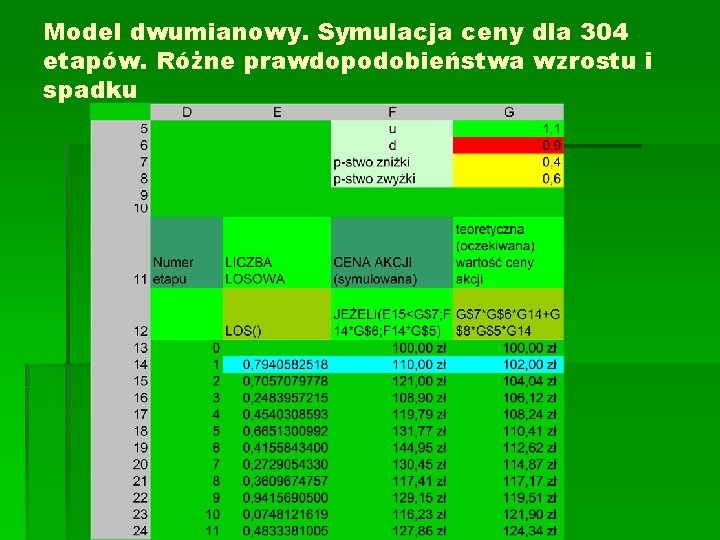
Model dwumianowy. Symulacja ceny dla 304 etapów. Różne prawdopodobieństwa wzrostu i spadku

Oczekiwana wartość ceny w (n+1)szym kroku § S 0=100 (cena początkowa) § ESn - oczekiwana wartość ceny po n – tym krokach § ESn+1= (1, 1 ESn ) • 0, 6 + (0, 9 ESn) • 0, 4 = = 1, 02 ESn § Ciąg (ESn) jest ciągiem geometrycznym o ilorazie 1, 02

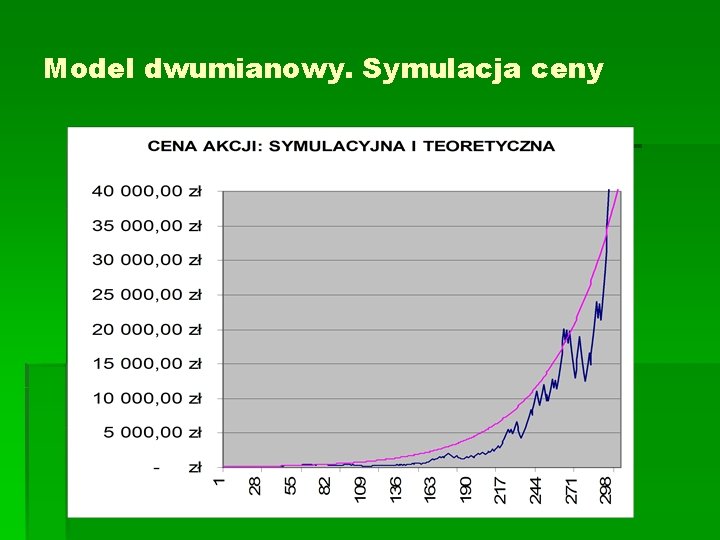
Model dwumianowy. Symulacja ceny

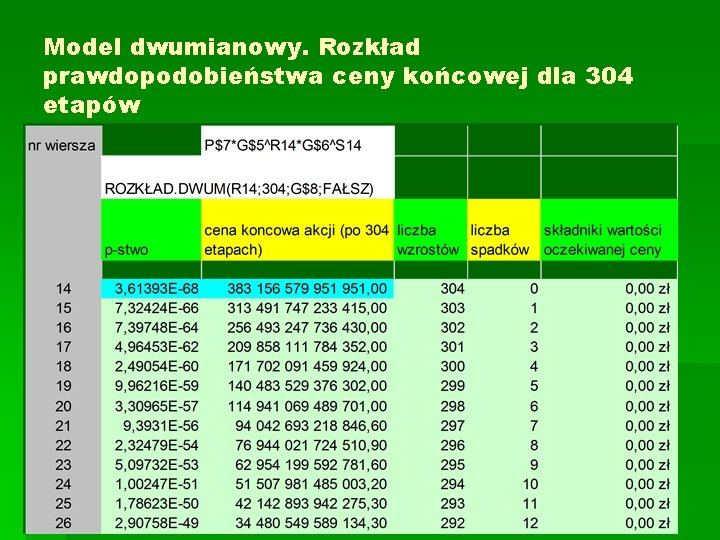
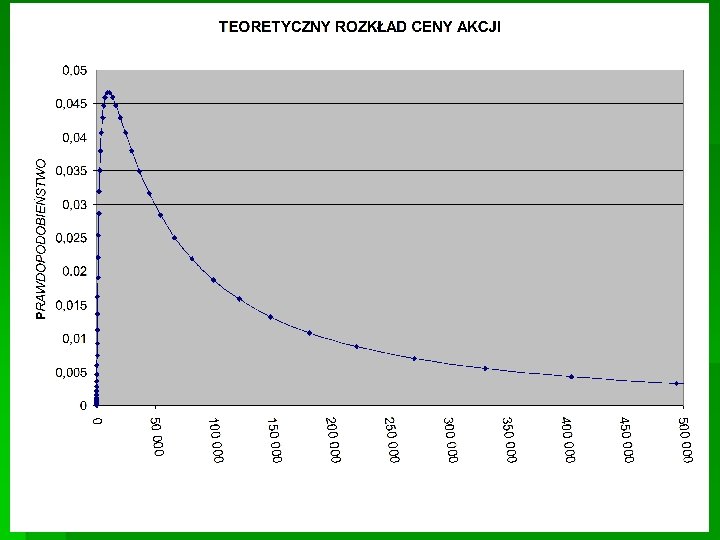
Model dwumianowy. Rozkład prawdopodobieństwa ceny końcowej dla 304 etapów

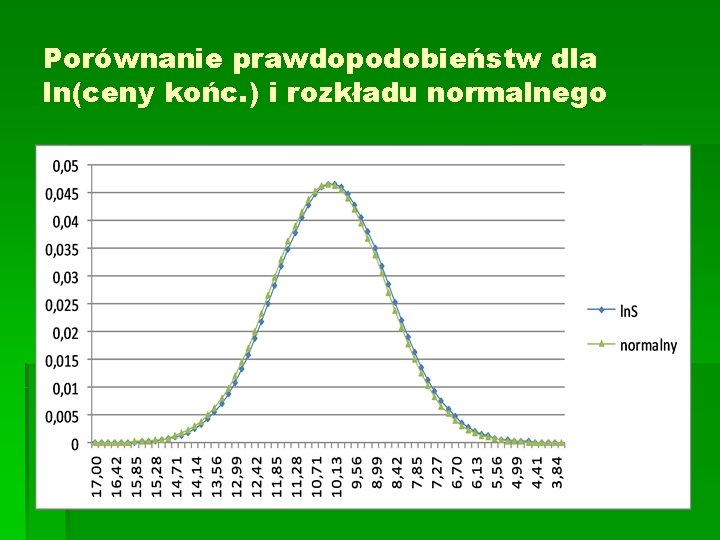
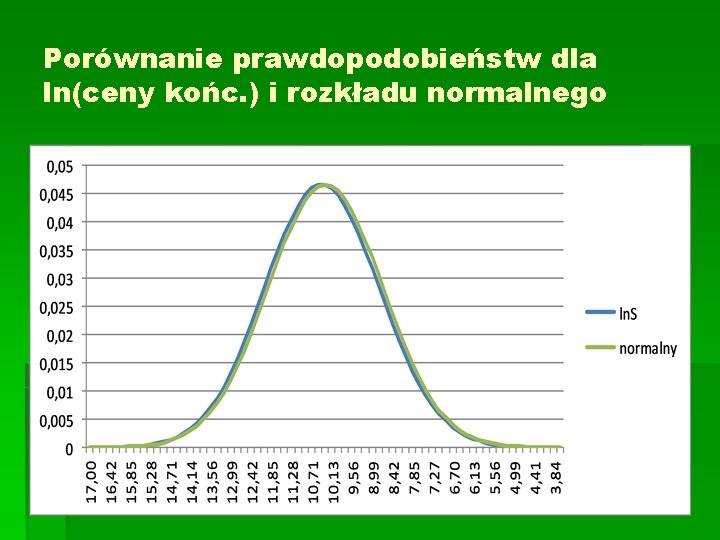
Porównanie prawdopodobieństw dla ln(ceny końc. ) i rozkładu normalnego

Porównanie prawdopodobieństw dla ln(ceny końc. ) i rozkładu normalnego