Modele zmiennoci aktyww ryzykownych Model addytywny Rozkad ceny

Modele zmienności aktywów ryzykownych Model addytywny Rozkład ceny końcowej – związek z rozkładem normalnym

Model addytywny zmienności aktywów z czasem dyskretnym Przyjmijmy następujące oznaczenia: S(0) - cena początkowa waloru S(k) - cena waloru w k-tym etapie. u(k) , k = 0, 1, 2, …n ciąg niezależnych zmiennych losowych o jednakowej wartości oczekiwanej μ oraz o tej samej wariancji równej σ2. Ciąg ten interpretujemy jako losowe fluktuacje.

Model addytywny Rozważmy model ceny aktywa postaci (1) S(k+1) = a S(k) + u (k) gdzie k=0, 1, 2, . . . zaś a jest pewną stałą rzeczywistą, dodatnią decydującą o trendzie głównym. Dla a > 1 trend główny jest wzrostowy. Znając wartości u(0), . . , u(n) można wyznaczyć S(1), S(2), …, S(n). W tym modelu cena waloru w dowolnym momencie zależy wyłącznie od ceny w momencie go poprzedzającym oraz od losowej fluktuacji.

Model addytywny Ze wzoru (1) otrzymujemy S(1) = a. S(0) + u(0) , S(2) = a. S(1) + u(1) = a[a. S(0) + u(0)] + u(1)= = a 2 S(0) + au(0) + u(1) S(3) = a. S(2)+u(2) = a [a 2 S(0) + au(0) + u(1)] +u(2)= = a 3 S(0) + a 2 u(0) + au(1) + u(2) Uwaga 1. Można pokazać, że dla każdego k: (2) S(k) = ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+a u(k-2) + u(k-1).

Model addytywny Rzeczywiście, dla k = 1 wzór jest prawdziwy (z definicji modelu). Zakładając prawdziwość dla k, z ciągu równości : S(k+1) = a S(k) + u (k)= a[ak. S(0) + ak-1 u(0) + ak-2 u(1) +… …+a u(k-2) + u(k-1)] + u (k) = =ak+1 S(0) + aku(0) + ak-1 u(1) +…+a 2 u(k-2) + au(k-1) + u (k) oraz indukcji matematycznej wynika prawdziwość wzoru (2)

Model addytywny. Wartość oczekiwana zmiennej S(k). Z elementarnych własności wartości oczekiwanej oraz z założenia E[u(k)]= μ dla każdego k mamy E[S(k)] =E( ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+ au(k-2) + u(k-1))= = ak. E[S(0)] + ak-1 E[u(0)] + ak-2 E[u(1)] +…+a. E[u(k-2)]+ E[u(k-1)] = ak. S(0) + ak-1 μ + ak-2 μ +…+a μ + μ (3) E[S(k)]= ak. S(0) + μ(1 -ak)/(1 -a), o ile a nie jest równe 1 (3’) E[S(k)]= S(0) + k μ, gdy a=1 (3’’) E[S(k)]= ak. S(0), gdy μ = 0

Model addytywny. Wariancja ceny Korzystając z podstawowych własności wariancji oraz założenia niezależności zmiennych losowych otrzymujemy Var [S(k)] = Var [ak. S(0) + ak-1 u(0) + ak-2 u(1) +…+ u(k-1)] = = Var [ak-1 u(0)] + Var[ak-2 u(1)] +…+Var[u(k-1)] = = (ak-1)2 Var [u(0)]+ (ak-2)2 Var [u(1)]+…+ a 2 Var [u(k-2)] + Var [u(k-1)]= = a 2(k-1)σ2+ a 2(k-2)σ2 +…+a 2σ2 +σ2 = = (1+a 2+a 4+…+a 2 k-2) σ2= σ2(1 - a 2 k)/ (1 -a 2), gdy a różne od 1 (4) (4’) Var [S(k)] = σ2(1 - a 2 k)/ (1 -a 2), gdy a różne od 1 Var [S(k)] = k σ2, dla a = 1

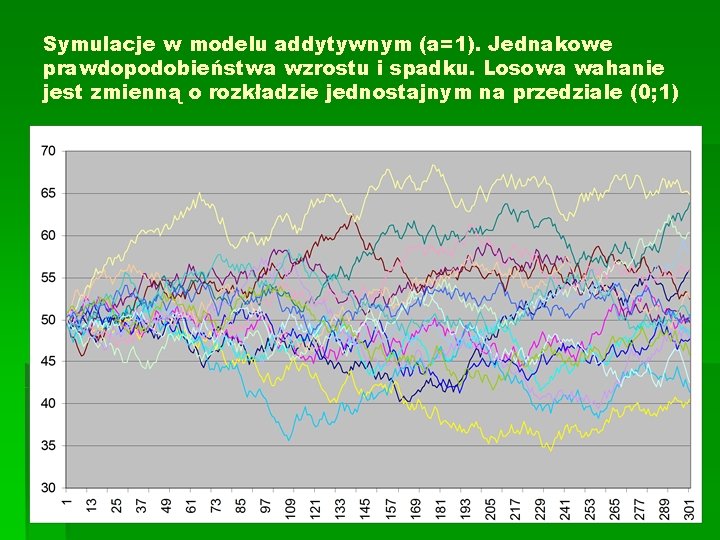
Symulacje w modelu addytywnym (a=1). Jednakowe prawdopodobieństwa wzrostu i spadku. Losowa wahanie jest zmienną o rozkładzie jednostajnym na przedziale (0; 1)

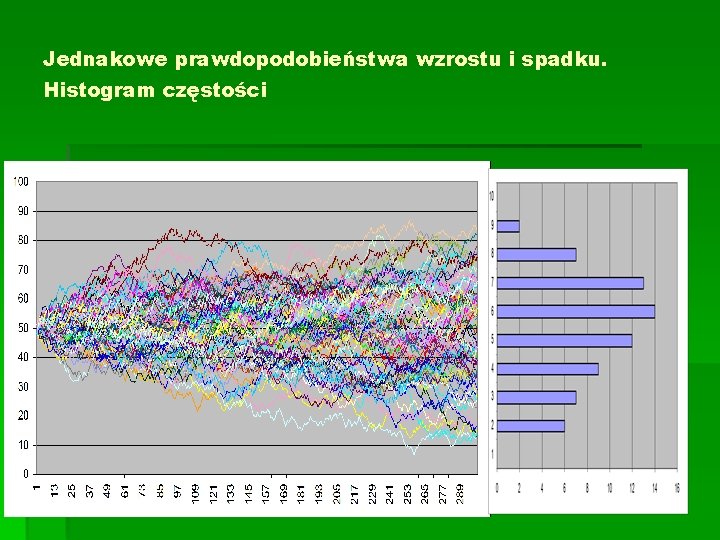
Jednakowe prawdopodobieństwa wzrostu i spadku. Histogram częstości

Model addytywny (przypadek a=1). Zmienne losowe u(k) o rozkładzie dwupunktowym S(k+1) = S(k) + u (k) u(k) mają rozkład dwupunktowy, k=0, 1, 2, . . . tzn. u(k) = σ lub u(k) = - σ, ( σ > 0 ) z jednakowymi prawdopodobieństwami S(n) = S(0) + u (1) +…+ u (n-1) (5) Sn= u (0) + u (1) +…+ u (n-1) (6) S(n) = S(0) + Sn Sn wyraża zmianę ceny po n etapach Wtedy: E[u (i)] = 0 Var [u (i)] = 0, 5(σ-0)2 + 0, 5(-σ-0)2 = σ2 E[Sn]= 0 Var Sn = Ʃni=1 Var [u (i)] = n σ2 Wzór na wariancję wynika z niezależności ciągu zmiennych losowych (u(i)). Z elementarnych własności wartości oczekiwanej i wariancji otrzymujemy E[S(n)]= S(0) Var S(n) = n σ2 Oznaczając przez σn odchylenie standardowe zmiennej Sn, mamy (7) σn = σ n

Centralne twierdzenie graniczne Standaryzacja zmiennej losowej Sn § S*n = (Sn-E(Sn))/σn Uwzględniając poprzednie wyliczenia § S*n= Sn/ σ n § TW (CTG) Niech (Xn) będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach (niekoniecznie dwupunktowych) oraz E Xi = m, Var Xi = σ2 dla i=1, …, n. Sn = X 1 + X 2 +… + Xn. Wtedy § (8) § (9) §

W przypadku m = 0 mamy W szczególności

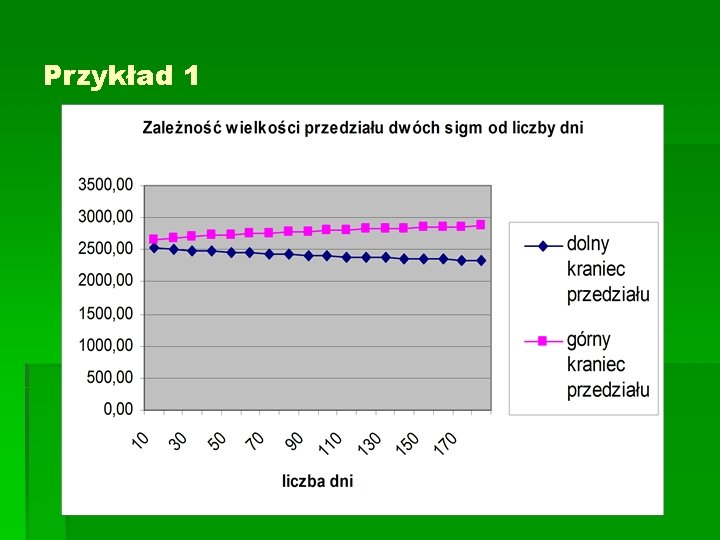
Przykład 1 § Kurs kontraktu futures na WIG 20 ma 2600 pt. Zakładamy, że każdego dnia kurs ma taką samą szansę na wzrost co na spadek o 10 punktów. W jakim przedziale znajdzie się z prawdopodobieństwem 0, 9545 kurs tego kontraktu po 30 dniach ? , (po 50? , po 100 ? ) § Zastosujemy centralne twierdzenie graniczne a w szczególności wykorzystamy przybliżenie § Ponieważ σ = 10, n=30 mamy więc § Otrzymaliśmy przedział na zmianę ceny, zatem uwzględniając S(n) = S(0) + Sn mamy §

Przykład 1 § Dla 50 i 100 dni mamy odpowiednio

Przykład 1

Przykład 2 § § § Kurs kontraktu futures na WIG 20 ma 2600 pt. Zakładamy, że każdego dnia kurs może zmienić się o 10 punktów, wzrost z prawdopodobieństwem 0, 55 lub spadek z prawdopodobieństwem 0, 45. W jakim przedziale znajdzie się z prawdopodobieństwem 0, 6827 kurs tego kontraktu po 30 dniach ? , (po 100 ? ) EXi=10*0, 55+(-10)*0, 45=1; War Xi = (10 -1)2 0, 55 + (-10 -1)2 0, 45 = 99 = σ2 ; σ = 9, 95 (zaokrąglenie do 2 miejsc)

Przykład 2 § Dla n=100 przeprowadzamy podobne wyliczenia § Otrzymujemy przedział (2600, 50; 2799, 50)

Centralne twierdzenie graniczne wersja Moivre’a – Laplace’a § Niech (Xn) będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach: dla każdego i (i=1, …, n), P{Xi =1} = p, P{Xi = 0} = q, p+q= 1, § Sn= X 1 + X 2+…+ Xn ; zmienna Sn ma rozkład dwumianowy: § Wtedy E Xi = p, Var Xi = pq § E Sn=np; Var Sn = npq § TW Przy powyższych oznaczeniach prawdziwa jest równość § (10) § lub równoważnie

Centralne twierdzenie graniczne wersja Moivre’a – Laplace’a § Ostatnie równości mogą być zapisane różne sposoby:

Przykład 3 § Cena akcji pewnej spółki wynosi 500 zł. Zakładamy, że każdego dnia kurs rośnie o 1 zł z prawdopodobieństwem 0, 55 i pozostaje niezmieniony z p-stwem 0, 45. Jakie jest prawdopodobieństwo, że po 1000 dniach cena będzie się mieściła w przedziale [1020; 1070] ?

Lokalne twierdzenie graniczne § Niech (Xn) będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach: dla każdego i (i=1, …, i=n) P{Xi =1} = p, P{Xi = 0} = q, p+q= 1, Sn= X 1 + X 2+…+ Xn ; zmienna Sn ma rozkład dwumianowy: § Wtedy E Xi = p, Var Xi = pq; E Sn=np; Var Sn = npq § TW. Przy powyższych oznaczeniach prawdziwa jest równość § (11) § Uwaga. Wszystkie liczby n, k, (n-k) muszą być dostatecznie duże by korzystać z ostatniego przybliżenia.