Ekonometryczne modele nieliniowe Wykad 7 Modele agodnego przejcia

Ekonometryczne modele nieliniowe Wykład 7 Modele łagodnego przejścia, sieci neuronowe w ekonometrii 1

Literatura • Timo Teräsvirta, Specification, Estimation, and Evaluation of Smooth Transition Autoregressive Models, Journal of the American Statistical Association, Vol. 89, No. 425 (Mar. , 1994), pp. 208 -218 • Dick van Dijk, Timo Teräsvirta and Philip Hans Franses, Smooth transition autoregressive models - A survey of recent developments, Econometric Reviews, 2002, vol. 21, issue 1, pp. 1 -47. 2

Literatura • Marcelo C. Medeiros & Timo Terasvirta, 2001, Statistical methods for modelling neural networks, Textos para discussão 445, Department of Economics PUC-Rio (Brazil). • Timo Teräsvirta, Dick van Dijk, Marcelo C. Medeiros, Linear models, smooth transition autoregressions, and neural networks forecasting macroeconomic time series: A re-examination, International Journal of Forecasting, Volume 21, Issue 4, 2005, pp. 755 -774. 3

Literatura Książka: • P. H. Frances, D. van Dijk, Non-linear time series models in empirical finance, Cambridge University Press, Cambridge, UK. 4

Przejście z modelu progowego… • Model z dwoma reżimami • …inaczej zapisany 5

Model STR • Smooth Transition (Auto-)Regression 6

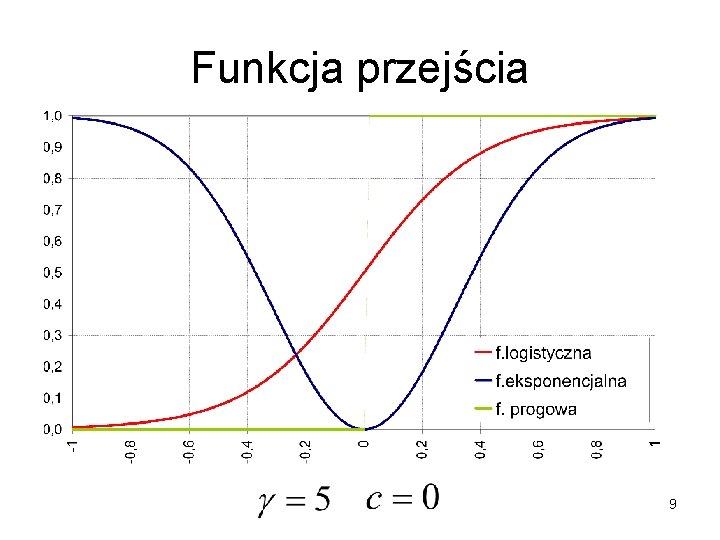
Funkcja przejścia • G – funkcja logistyczna • gdy , to model liniowy , to model progowy 7

Funkcja przejścia • G – funkcja eksponencjalna • gdy , to model liniowy 8

Funkcja przejścia 9

Estymacja Teräsvirta (1994) „conditional least squares”: 10

Estymacja • Estymator zgodny i asymptotycznie normalny • Problemy techniczne metody gradientowej: – ESTR: silnie skorelowane z parametrami (bez stałej) 1. standardyzuj wykładnik w G przez podzielenie go przez wariancję y 2. ustal startową wartość , np. 3. jeśli algorytm gradientowy nie zbiega, to „grid search” - 11

Estymacja • Estymator zgodny i asymptotycznie normalny • Problemy techniczne metody gradientowej: – LSTR: do oszacowania i gdy , to model TR (duży błąd oszacowania ) 1. Skaluj parametry startowe (zmniejsz i zwiększ c [? ? ]), podziel wykładnik w G przez odchylenie stand. y 2. Jeśli algorytm gradientowy nie zbiega, to „grid search”- c 12

Estymacja • Możliwa estymacja MNK pod warunkiem, że znane 13

Specyfikacja • wybór modelu liniowego (np. AR(p)) • testowanie liniowości modelu (przeciw STR) dla różnych zmiennych przejścia (transition variables) + wybór optymalnej zmiennej przejścia • wybór między LSTR i ESTR 14

Testowanie modelu STR • Hipotezy • Problem z parametrami nieidentyfikowalnymi przy H 0 niestandardowe rozkłady statystyk testowych 15

Testowanie modelu STR • Luukkonen, Saikkonen, Teräsvirta (1988): – Rozwinięcie modelu STR w szereg Taylora wokół – Zastosowanie testu LM 16

Testowanie LSTR • Szereg Taylora 1. rzędu: • Przy H 0 …dlatego test LM 17

Testowanie LSTR c. d. • Testowanie ( ) równoważne z • Standardowy test LM (szczegóły później) – Nazywany tutaj: „LM-type test” • Problem: kiedy , trzeba usunąć z „testowego” modelu regresji (współliniowość) – test nie nadaje się do testowania zmian stałej 18

Testowanie LSTR c. d. • Rozwiązanie: szereg Taylora 3. rzędu bez lub uproszczona wersja: • Test LM 19

Testowanie ESTR • Rozwinięcie ESTR w szereg Taylora 1. rzędu: • lub uwzględniając 2 punkty przegięcia w ESTR – rozwinięcie 2. rzędu: 20

Testowanie ESTR c. d. • Test typu LM 21

Obliczanie statystyk LM • Oszacuj model przy założeniu H 0 • Oszacuj „testową” regresję: y x, xz • Statystyka: lub w małych próbach: 22

Autokorelacja składnika losowego • Niech • Oszacuj model STR i oblicz reszty • Oblicz gdzie • Oszacuj model liniowy i oblicz R-kwadrat: • Rozszerzenie testu Godfreya (1979): H 0: brak autokorelacji 23

Test pozostałej nieliniowości • Model rozszerzony: • H 0: lub • Zamień G 2 na rozwinięcie w szereg Taylora 3. rzędu: • Po przekształceniu, H 0: 24

Test pozostałej nieliniowości • Niech • Oszacuj model STR i oblicz reszty • Oblicz gdzie • Oszacuj model liniowy i oblicz R-kwadrat: • Statystyka LM 25

Wybór funkcji przejścia • Sekwencja testów (statystyki LM): • Reguła decyzyjna: – Jeśli empiryczny poziom istotności (p-value) najmniejszy dla H 02 , to wybierz model ESTR – Jeśli empiryczny poziom istotności najmniejszy dla H 01 lub H 03 , to wybierz model LSTR 26

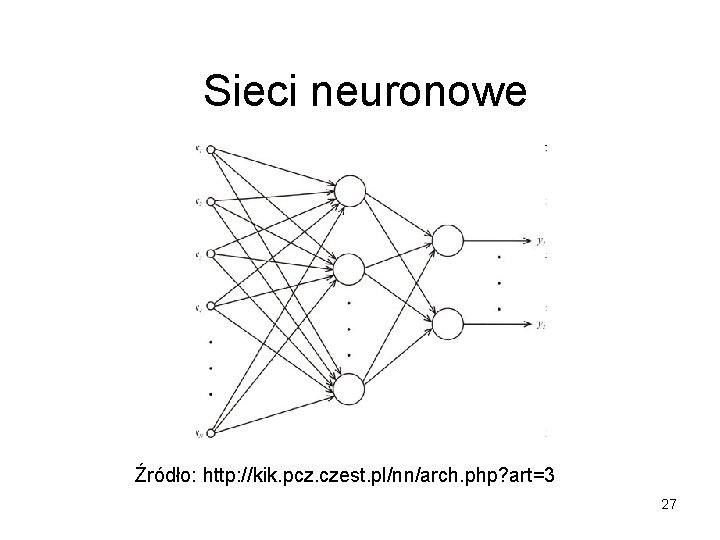
Sieci neuronowe Źródło: http: //kik. pcz. czest. pl/nn/arch. php? art=3 27

Sieci neuronowe • Model z jedną warstwą ukrytą • Funkcja logistyczna F lub inna sigmoidalna 28

Sieci neuronowe • Dokładne dopasowanie modelu do danych – możliwe dowolnie dokładne przybliżenie funkcji ciągłej – nie proces generujący dane, ale model przybliżający prawdziwy proces • Prognozowanie • Ekonomiczna interpretacja zależności? Nie. 29

Identyfikowalność parametrów • 3 problemy z identyfikowalnością – h! permutacji neuronów (funkcji przejścia) ma taką samą wartość funkcji wiarygodności – dodatkowo: – duża liczba funkcji przejścia • Rozwiązanie: – restrykcje: – odpowiednia specyfikacja modelu 30

Budowa modelu • Wybór zmiennych • Wybór liczby funkcji przejścia – wymaga estymacji modelu 31

Budowa modelu • Wybór zmiennych – przybliżenie sieci neuronowej przez wielomian k-tego rzędu – szacowanie modeli i optymalizacja kryterium informacyjnego: AIC, SBIC 32

Estymacja modelu • Metoda Największej Wiarygodności – równoważna: Nieliniowa MNK • Przydatna reparametryzacja 33

Estymacja modelu • Wektor parametrów • Standaryzowanie zmiennych wejściowych: Var(x)=1 • Możliwość „koncentracji” funkcji wiarygodności – tzn. szacowanie parametrów w grupach 34

Estymacja c. d. • Przyjmij za znane: • Zbuduj macierz Z dla regresji: 35

Estymacja c. d. • Szacuj parametry MNK: • Parametry szacuj minimalizując sumę kwadratów reszt – algorytmy optymalizacji: BFGS, Levenberg. Marquardt 36

Wybór liczby funkcji przejścia • Metoda „od małego do dużego” – dodawanie neuronów (hidden units) • Testowanie czy h+1 neuron zbędny 37

Testowanie funkcji przejścia • Rozwinięcie modelu w szereg Taylora 3. rzędu: • Oszacuj model z h neuronami i oblicz reszty • Wyznacz wektor „score” – Jeśli i nie są ortogonalne, to oszacuj regresję tych zmiennych i wyznacz reszty 38

Testowanie c. d. • Oblicz • Oszacuj regresję na i • Oblicz reszty oraz 39

Testowanie c. d. • Statystyka: z m stopniami swobody • W małych próbach: ma w przybliżeniu rozkład F(m, T-n-m) 40

Ewaluacja modelu • Testy aukorelacji, niestabilności parametrów • Analiza prognoz 41