Kontrakty futures Ceny futures ceny kasowe konwergencja Wykresy

Kontrakty futures Ceny futures, ceny kasowe, konwergencja Wykresy St, Ft, ft Pojęcie bazy Ryzyko bazy w strategii zabezpieczającej Badanie własności addytywnego modelu zmienności kursu kontraktu

Ceny futures, ceny kasowe. Konwergencja § Z kontraktem towarowym futures związana jest cena dostawy (K). § Dzięki dziennym rozliczeniom kontraktu jego wartość na koniec dnia, stale osiąga zero § Cena kontraktu jest różna (na ogół wyższa) od ceny kasowej aktywów. ( Ft = St er (T - t)) § Wraz ze zbliżaniem się terminu dostawy ceny te zbliżają się do siebie, by zrównać się w chwili wygaśnięcia kontraktu

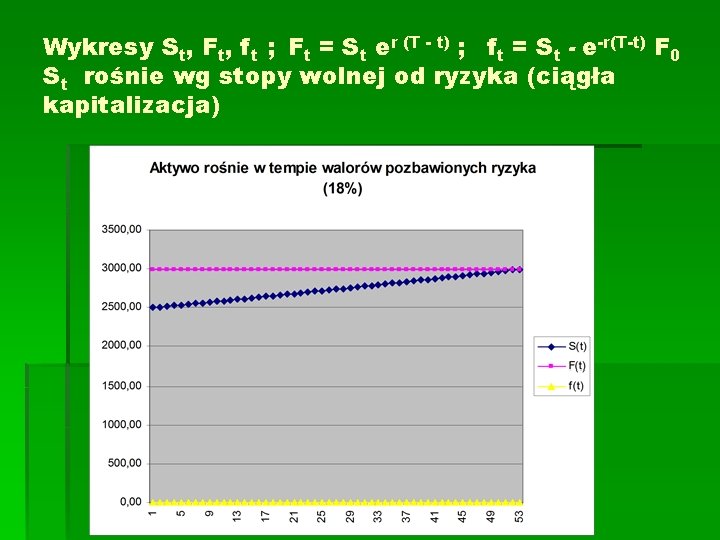
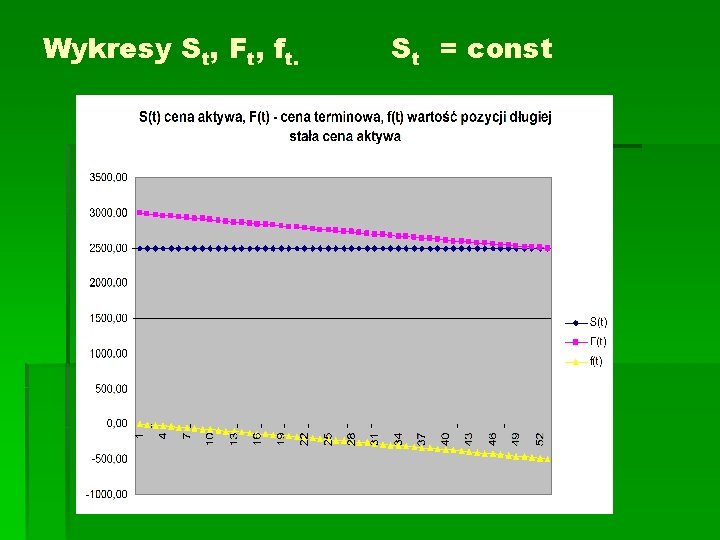
Wykresy St, Ft, ft ; Ft = St er (T - t) ; ft = St - e-r(T-t) F 0 St rośnie wg stopy wolnej od ryzyka (ciągła kapitalizacja)

Wykresy St, Ft, ft. St = const

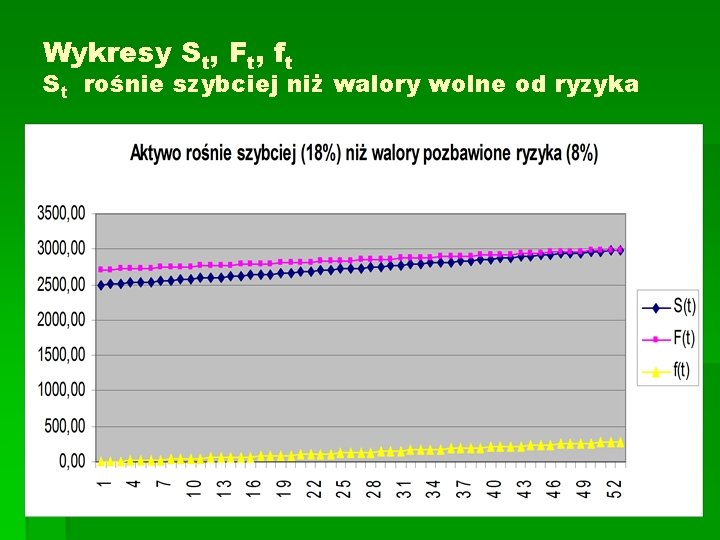
Wykresy St, Ft, ft St rośnie szybciej niż walory wolne od ryzyka

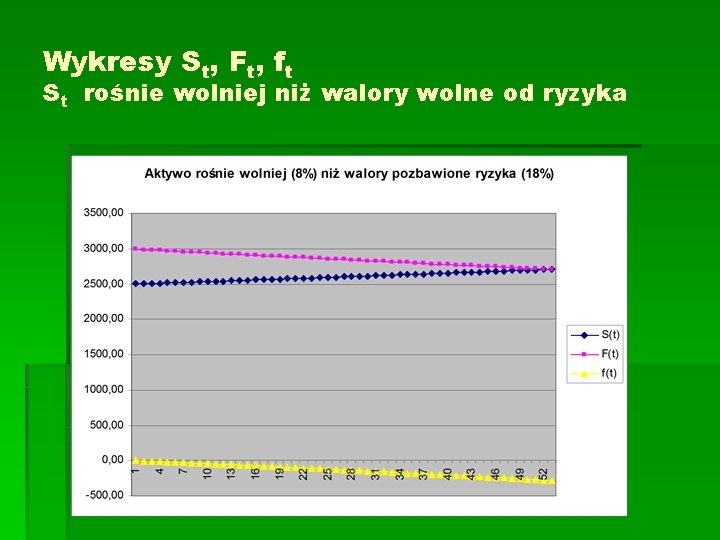
Wykresy St, Ft, ft St rośnie wolniej niż walory wolne od ryzyka

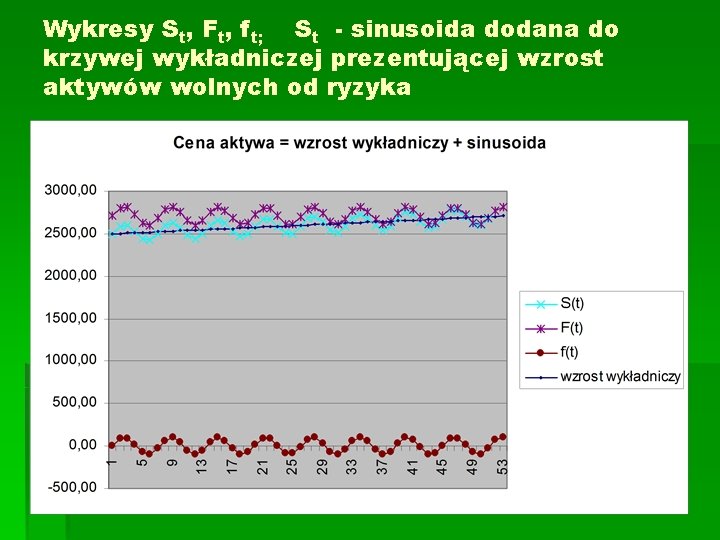
Wykresy St, Ft, ft; St - sinusoida dodana do krzywej wykładniczej prezentującej wzrost aktywów wolnych od ryzyka

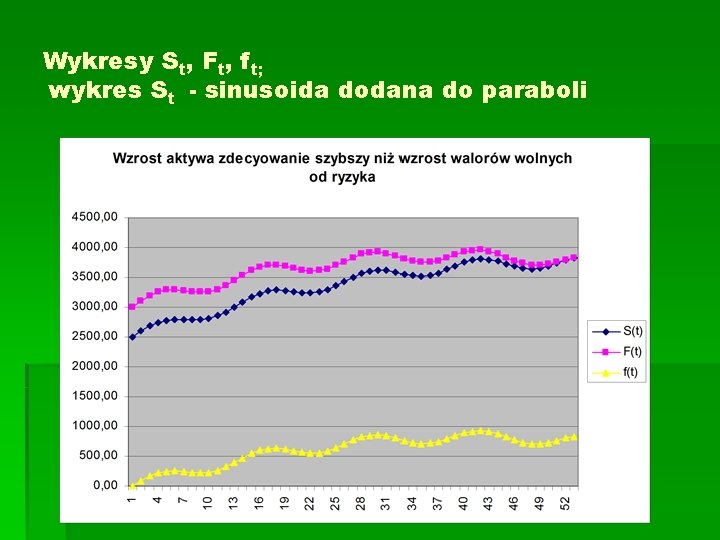
Wykresy St, Ft, ft; wykres St - sinusoida dodana do paraboli

Pojęcie bazy Ryzyko bazy w strategii zabezpieczającej § § § § Baza = (cena kasowa aktywów objętych strategią zabezpieczającą) – (cena terminowa kontraktów) S 1 cena kasowa w chwili t 1 S 2 cena kasowa w chwili t 2 F 1 cena kontraktu futures w chwili t 1 F 2 cena kontraktu futures w chwili t 2 B 1 wartość bazy w chwili t 1 B 2 wartość bazy w chwili t 2 W chwili t 1 rozpoczynamy strategie zabezpieczającą, zakończoną w chwili t 2 § Przykład. Ceny kasowa i terminowa w chwili t 1 wynoszą 2, 2 oraz 2, 5 $ zaś w chwili t 2 wynoszą odpowiednio 1, 9 i 2 $. § B 1= S 1 - F 1; B 2 = S 2 – F 2

Pojęcie bazy Ryzyko bazy w strategii zabezpieczającej § Załóżmy, że inwestor zamierza sprzedać aktywa w chwili t 2 (wcześniej ma długa pozycję na aktywach). § W chwili t 1 zajmuje krótką pozycję na kontrakcie futures § W chwili t 2 otrzymuje ze sprzedaży za walor S 2 oraz F 1 - F 2 z kontraktu § Efektywna cena uzyskana z zastosowania strategii to S 2 + F 1 - F 2 = F 1 + B 2 § W rozważanym przypadku to 2, 5 $ + (-0, 1) $ = 2, 4 $ § Wielkość B 2 jest w chwili t 1 wartością nieznaną, stanowi więc źródło ryzyka zwanego ryzykiem bazy

Pojęcie bazy Ryzyko bazy w strategii zabezpieczającej Załóżmy, że inwestor zamierza kupić aktywa w chwili t 2. § W chwili t 1 zajmuje długą pozycję na kontrakcie futures § W chwili t 2 kupuje za S 2 walor oraz uzyskuje F 2 -F 1 z kontraktu § Efektywna cena zakupu uzyskana z zastosowania strategii to S 2 – (F 2 -F 1) = S 2 – F 2 + F 1 = F 1 + B 2 § W rozważanym przypadku to 2, 5 $ + (-0, 1) $ = 2, 4 $ § W obu przypadkach obie ceny: sprzedaży i zakupu okazały się równe i mniejsze od ceny terminowej z chwili t 1

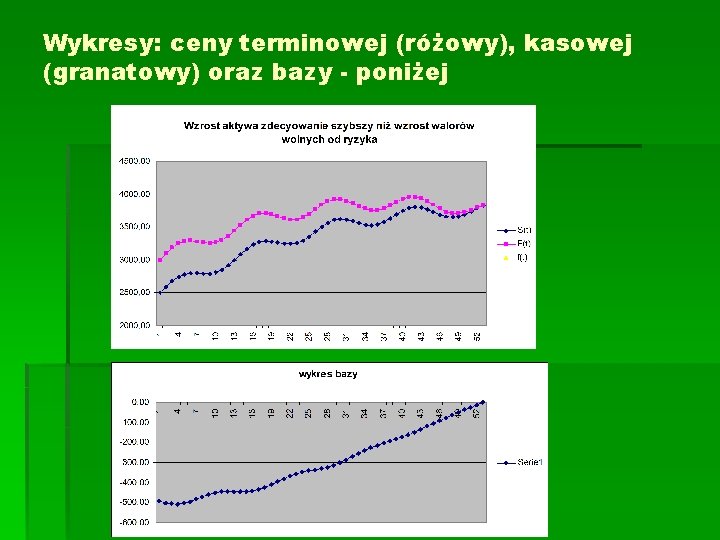
Wykresy: ceny terminowej (różowy), kasowej (granatowy) oraz bazy - poniżej

Badanie własności addytywnego modelu zmienności kursu kontraktu § Prawdopodobieństwo skoku ceny powyżej ustalonej wartości w skończonej liczbie kroków § Powrót do źródła. Prawdopodobieństwo powrotu do źródła (osiągnięcia ceny początkowej) w chwili 2 n. § Oczekiwana liczba powrotów w czasie błądzenia o długości 2 n kroków § Prawdopodobieństwo długich prowadzeń (pozostawania ceny ponad ustaloną wartością) § Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego. (Oczekiwany kwadrat różnicy ceny końcowej i początkowej)

Badanie własności addytywnego modelu zmienności kursu kontraktu § (a) § Załóżmy, że kurs kontraktu na zamknięciu każdej sesji wzrasta lub spada o 10 punktów z jednakowym prawdopodobieństwem. Inwestor zajął kiedyś długą pozycję na kontrakcie ale od tamtej chwili kurs spadł o 90 punktów. Do wygaśnięcia kontraktu pozostało jeszcze tylko 20 dni. Obliczymy prawdopodobieństwo uzyskania jakiegokolwiek zysku z inwestycji, zakładając, że inwestor utrzyma pozycję do wygaśnięcia.

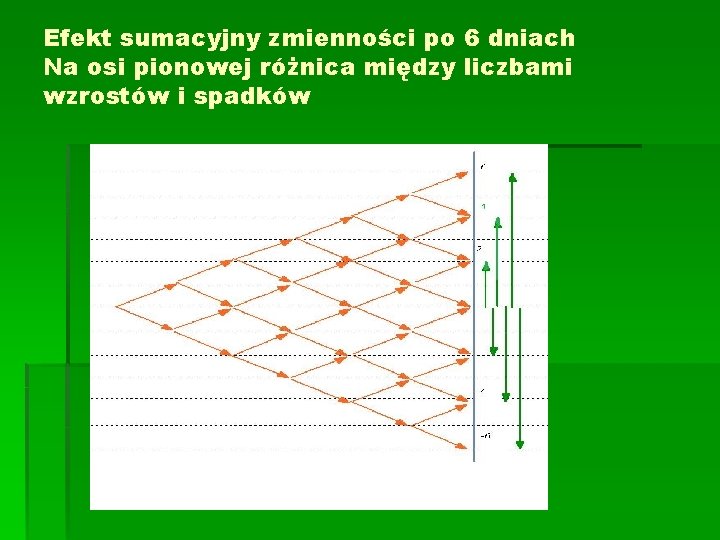
Efekt sumacyjny zmienności po 6 dniach Na osi pionowej różnica między liczbami wzrostów i spadków

Addytywny model zmienności kursu kontraktu § Przy 20 dniach do wygaśnięcia (20 próbach Bernoulliego) inwestor osiągnie zysk w następujących przypadkach liczb wzrostów i spadków : (15, 5); (16, 4); (17, 3); (18, 2); (19, 1); (20, 0). Sumując prawdopodobieństwa uzyskania odpowiedniej liczby sukcesów (wzrostów) obliczamy żądane prawdopodobieństwo. Stosujemy wzór na prawdopodobieństwo k sukcesów w n próbach Bernoulliego

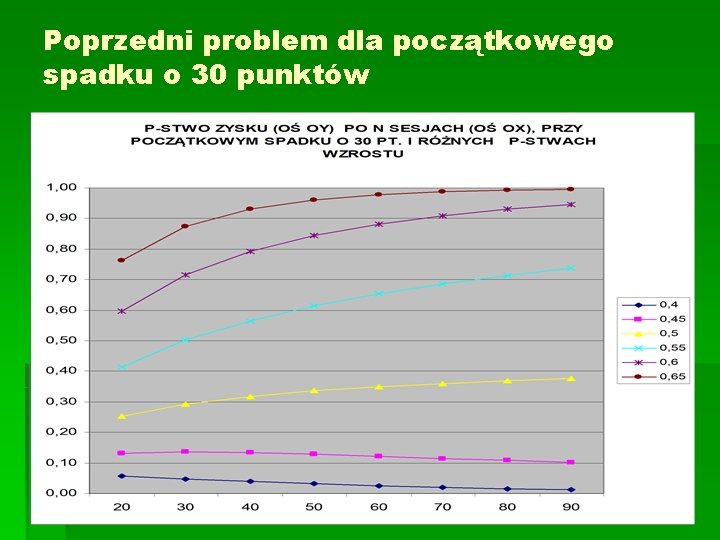
Addytywny model zmienności kursu kontraktu § (b) Przeprowadzimy podobne obliczenia dla różnej liczby dni do wygaśnięcia kontraktu: 30, 40, 50, 60, 70, 80 oraz sporządzimy wykres prawdopodobieństwa uzyskania jakiegokolwiek zysku z inwestycji od liczby dni pozostających do wygaśnięcia. § (c) Sporządzimy wykresy prawdopodobieństwa uzyskania jakiegokolwiek zysku z inwestycji w zależności od liczby dni do wygaśnięcia, dla różnych prawdopodobieństw wzrostu kursu (0, 4; 0, 45; 0, 55; 0, 65) § Dla każdej liczby dni należy ustalić wszystkie przypadki w których różnica między liczbą sukcesów i porażek jest nie mniejsza niż 10. Np. dla 60 liczby sukcesów sprzyjające zdarzeniu to: 35, 36, …, 60, dla 70 liczby sukcesów to: 40, 41, 42, …, 70

Addytywny model zmienności kursu kontraktu § Załóżmy, jak poprzednio, że kurs kontraktu na zamknięciu każdej sesji wzrasta lub spada o 10 punktów z pewnym prawdopodobieństwem. Inwestor zajął kiedyś długą pozycję na kontrakcie ale od tamtej chwili kurs spadł o 50 punktów. § Sporządzimy wykresy prawdopodobieństwa uzyskania jakiegokolwiek zysku z inwestycji w zależności od liczby dni do wygaśnięcia, dla różnych prawdopodobieństw wzrostu kursu § (0, 4; 0, 45; 0, 55; 0, 65)

Poprzedni problem dla początkowego spadku o 30 punktów

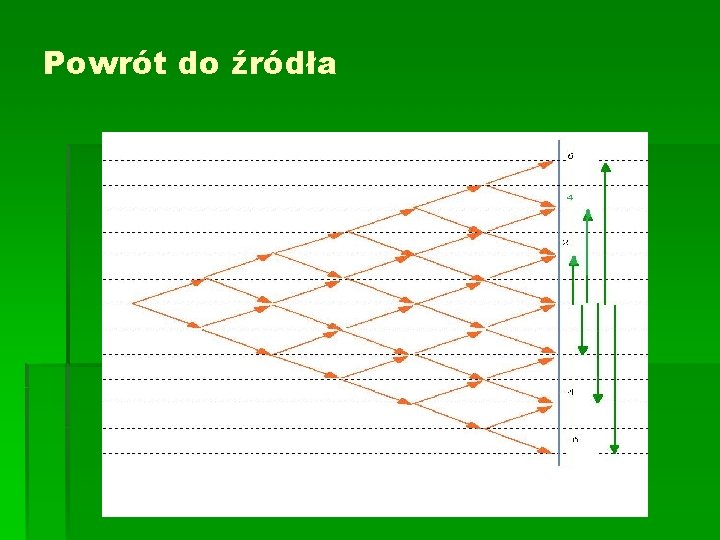
Powrót do źródła § Punkt startowy błądzącej cząstki nazywamy źródłem § Mówimy, że pierwszy powrót cząstki do źródła nastąpił w k- tym kroku, jeżeli cząstka ta w krokach wcześniejszych nie była rejestrowana w punkcie startu Zakładamy że kurs kontraktu w każdym dniu wzrasta o k punktów z prawdopodobieństwem p lub spada o k punktów z prawdopodobieństwem q. § Jakie jest prawdopodobieństwo, że kurs kontraktu powróci po dokładnie 2 n dniach do poziomu przy którym inwestor zajął pozycję? § Jaka jest oczekiwana liczba powrotów do tego poziomu na przestrzeni 2 n dni ?

Powrót do źródła

Prawdopodobieństwo powrotu do źródła w chwili 2 n § Powroty do źródła mogą następować tylko w momentach parzystych, w przypadku gdy liczba kroków w górę jest taka sama jak w dół § Skorzystamy ze schematu Bernoulliego § Prawdopodobieństwo powrotu do źródła w dokładnie 2 n krokach przy błądzeniu asymetrycznym

Oczekiwana liczba powrotów do źródła w 2 n krokach § Po 2 krokach, błądzenie może zakończyć się w zerze lub poza nim. Oczekiwana liczba powrotów po 2 krokach wynosi więc § Po 4 krokach, błądzenie może zakończyć się w zerze lub poza nim. Oczekiwana liczba powrotów po 4 krokach wynosi więc § itd. .

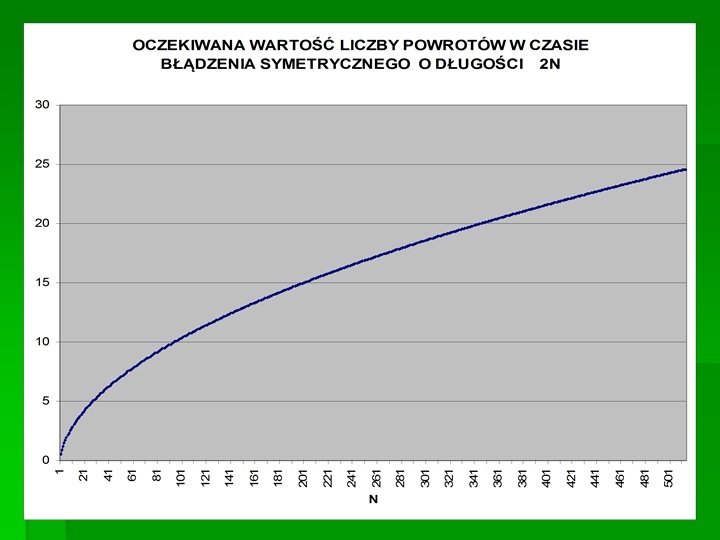
Oczekiwana liczba powrotów w czasie błądzenia o długości 2 n kroków = =

Powrót do źródła excel

Prawdopodobieństwo długich prowadzeń § Załóżmy, że kurs kontraktu na zamknięciu każdej sesji wzrasta lub spada o 10 punktów z jednakowym prawdopodobieństwem. Inwestor zajmuje długą pozycję na kontrakcie. Zakładając, że po 20 dniach kurs kontraktu będzie wyższy o 20 punktów obliczymy prawdopodobieństwo tego, że kurs będzie cały czas powyżej kursu zakupu.

Prawdopodobieństwo długich prowadzeń § Oznaczając liczbę sukcesów przez a, porażek przez b, mamy a + b = 20; a - b = 2. § Aby kurs kontraktu był cały czas powyżej kursu zakupu, po każdym dniu liczba sukcesów musi być większa niż liczba porażek. Sytuacja ta odpowiada modelowi tzw. długich prowadzeń. (W. Feller „Wstęp o rachunku prawdopodobieństwa” t. 1) § Okazuje się prawdopodobieństwo długiego prowadzenia (kurs będzie cały czas powyżej kursu zakupu) § to liczba (a-b)/(a+b)

Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego § di - odległość od źródła i-tego punktu docelowego § pi - prawdopodobieństwo dotarcia do i-tego punktu docelowego § Niech w każdym kroku cząstka przemieszcza się w górę lub w dół o jeden (jednostkowy wzrost lub spadek ceny). Obliczymy wartość oczekiwanego kwadratu odległości od punktu startu po n krokach. (oczekiwanego kwadratu różnicy ceny końcowej i początkowej)

Oczekiwany kwadrat odległości od źródła po 6 oraz po 7 krokach błądzenia symetrycznego

Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego

Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego § Ponieważ oczekiwana pozycja docelowa przy błądzeniu symetrycznym to punkt zerowy, więc pojęcie oczekiwanego kwadratu odległości od źródła pokrywa się z wariancją wartości docelowej błądzenia. § W języku zmiennych losowych, błądzenie w n krokach jest sumą n niezależnych zmiennych losowych o rozkładzie dwupunktowym Yn= X 1 + X 2+…+ Xn § gdzie Xi przyjmuje wartości 1 lub (-1) z jednakowymi prawdopodobieństwami, wariancja takiej zmiennej wynosi 1. Z niezależności zmiennych Xi wynika, że wariancja zmiennej Yn jest sumą wariancji poszczególnych Xi, co daje n. § Zatem oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego wynosi n.

Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego § Zatem § Pierwiastek z oczekiwanego kwadratu odległości od źródła jest więc odchyleniem standardowym wartości docelowej błądzenia, czyli zmiennej Yn

Oczekiwany kwadrat odległości od źródła po n krokach błądzenia symetrycznego, przy jednostkowym kroku długości d Oczekiwany kwadrat odległości od źródła w tym przypadku jest iloczynem tej wielkości dla jednostkowego kroku oraz d 2 Pierwiastek z oczekiwanego kwadratu odległości od źródła, czyli odchylenie standardowe wartości docelowej błądzenia wynosi więc d n

Literatura Kontrakty terminowe i opcje. Wprowadzenie J. Hull Warszawa 1997 Teoria inwestycji finansowych D. Luenberger Wstęp o rachunku prawdopodobieństwa t. 1 W. Feller Instrumenty pochodne – sympozjum matematyki finansowej. Kraków UJ 1997 Inwestycje K. Jajuga, T. Jajuga PWN 2008 Rynkowe instrumenty finansowe A. Sopoćko PWN 2005