Midterm Review Calculus Derivative relationships dsin xdx cos





















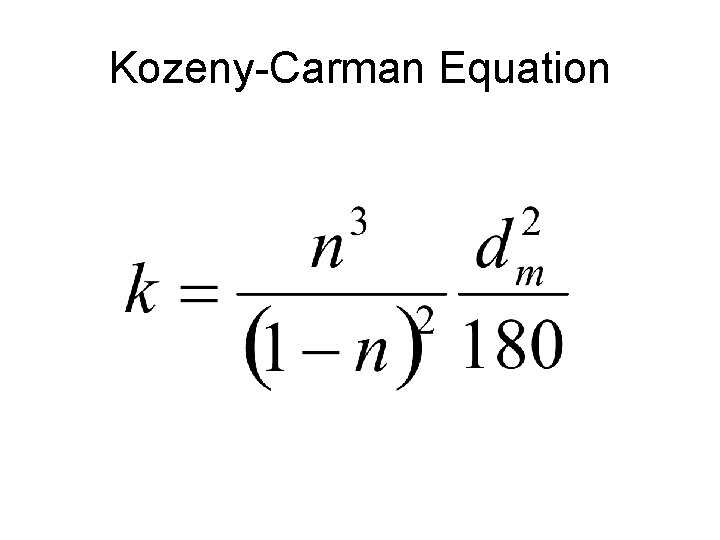











- Slides: 53

Midterm Review

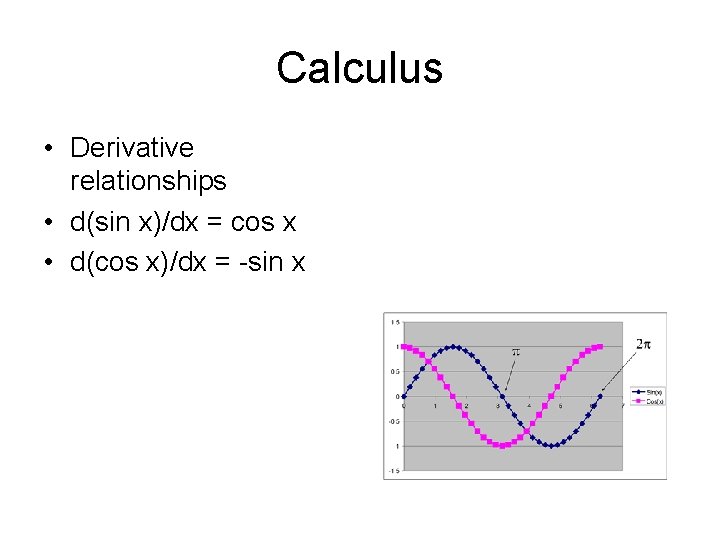
Calculus • Derivative relationships • d(sin x)/dx = cos x • d(cos x)/dx = -sin x

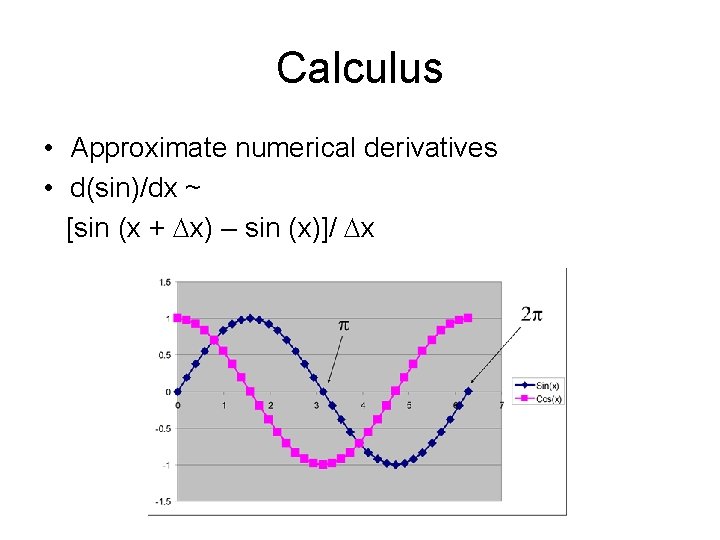
Calculus • Approximate numerical derivatives • d(sin)/dx ~ [sin (x + Dx) – sin (x)]/ Dx

Calculus • Partial derivatives • h(x, y) = x 4 + y 3 + xy • The partial derivative of h with respect to x at a y location y 0 (i. e. , ∂h/∂x|y=y 0), • Treat any terms containing y only as constants – If these constants stand alone they drop out of the result – If the constants are in multiplicative terms involving x, they are retained as constants • Thus ∂h/ ∂x|y=y 0 = 4 x 3 + y 0

Ground Water Basics • • Porosity Head Hydraulic Conductivity Transmissivity

Porosity Basics • Porosity n (or f) • Volume of pores is also the total volume – the solids volume

Porosity Basics • Can re-write that as: • Then incorporate: • Solid density: rs = Msolids/Vsolids • Bulk density: rb = Msolids/Vtotal • rb/rs = Vsolids/Vtotal

Cubic Packings and Porosity Simple Cubic n = 0. 48 Body-Centered Cubic Face-Centered Cubic n = 0. 26 http: //members. tripod. com/~Epp. E/images. htm n = 0. 26

FCC and BCC have same porosity http: //uwp. edu/~li/geol 200 -01/cryschem/ • Bottom line for randomly packed beads: n ≈ 0. 4 Smith et al. 1929, PR 34: 1271 -1274

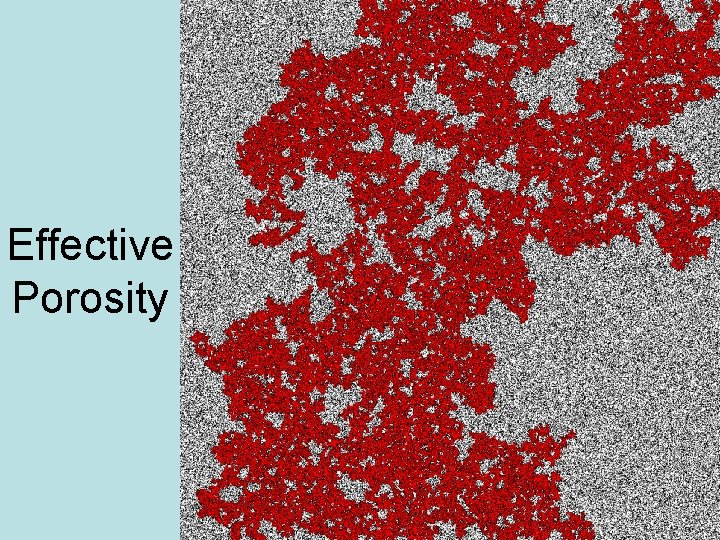
Effective Porosity

Effective Porosity

Porosity Basics • Volumetric water content (q) – Equals porosity for saturated system

Ground Water Flow • • Pressure and pressure head Elevation head Total head Head gradient Discharge Darcy’s Law (hydraulic conductivity) Kozeny-Carman Equation

Multiple Choice: Water flows…? • Uphill • Downhill • Something else

Pressure • Pressure is force per unit area • Newton: F = ma – F force (‘Newtons’ N or kg m s-2) – m mass (kg) – a acceleration (m s-2) • P = F/Area (Nm-2 or kg m s-2 m-2 = kg s-2 m-1 = Pa)

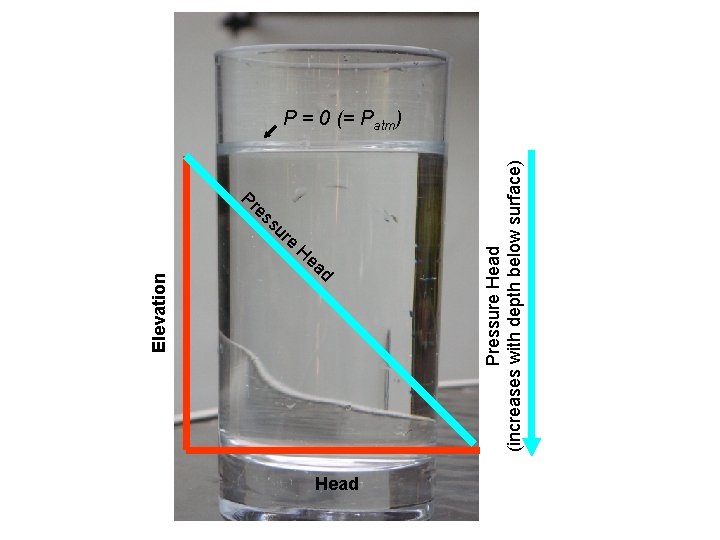
Pressure and Pressure Head • Pressure relative to atmospheric, so P = 0 at water table • P = rghp – r density – g gravity – hp depth

Elevation Pr es su re H ea d Head Pressure Head (increases with depth below surface) P = 0 (= Patm)

Elevation Head • Water wants to fall • Potential energy

Head El at io ev n ad He Elevation Head (increases with height above datum) Elevation datum

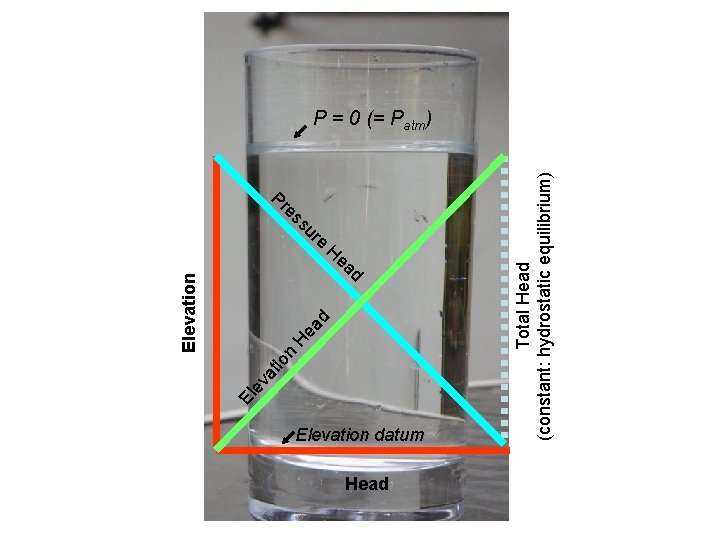
Total Head • For our purposes: • Total head = Pressure head + Elevation head • Water flows down a total head gradient

at io ev n ad He Pr es su re H ea d Elevation datum Head Total Head (constant: hydrostatic equilibrium) El Elevation P = 0 (= Patm)

Head Gradient • Change in head divided by distance in porous medium over which head change occurs • dh/dx [unitless]

Discharge • Q (volume per time) Specific Discharge/Flux/Darcy Velocity • q (volume per time per unit area) • L 3 T-1 L-2 → L T-1

Darcy’s Law • Q = -K dh/dx A where K is the hydraulic conductivity and A is the cross-sectional flow area 1803 - 1858 www. ngwa. org/ ngwef/darcy. html

Darcy’s Law • Q = K dh/dl A • Specific discharge or Darcy ‘velocity’: qx = -Kx ∂h/∂x … q = -K grad h • Mean pore water velocity: v = q/ne

Intrinsic Permeability L T-1 L 2
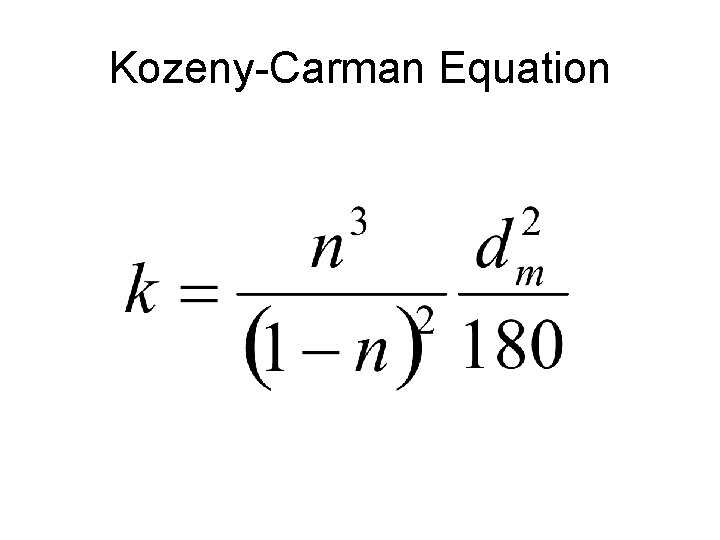
Kozeny-Carman Equation

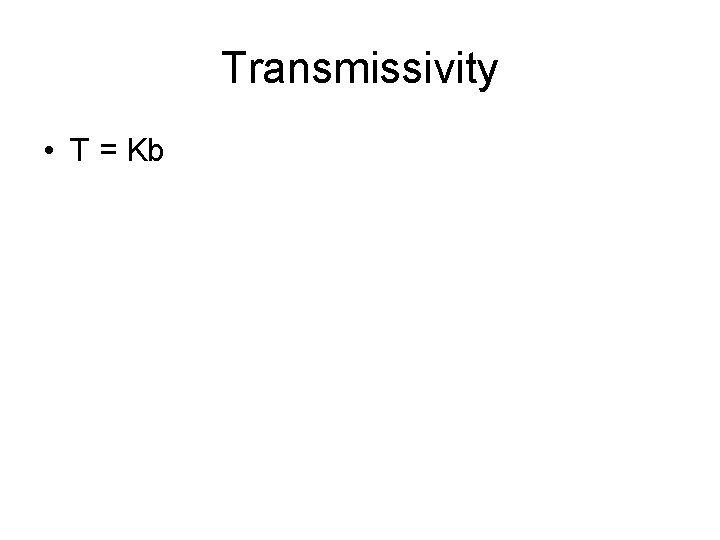
Transmissivity • T = Kb

Potential/Potential Diagrams • Total potential = elevation potential + pressure potential • Pressure potential depends on depth below a free surface • Elevation potential depends on height relative to a reference (slope is 1)

Darcy’s Law • Q = -K dh/dl A • Q, q • K, T

Mass Balance/Conservation Equation • • • I = inputs P = production O = outputs L = losses A = accumulation

Derivation of 1 -D Laplace Equation qx | x • • Dz Inflows - Outflows = 0 (q|x - q|x+Dx)Dy. Dz = 0 q|x – (q|x +Dx dq/dx) = 0 dq/dx = 0 (Continuity Equation) (Constitutive equation) qx|x+Dx Dx Dy

General Analytical Solution of 1 -D Laplace Equation

Particular Analytical Solution of 1 -D Laplace Equation (BVP) BCs: - Derivative (constant flux): e. g. , dh/dx|0 = 0. 01 - Constant head: e. g. , h|100 = 10 m After 1 st integration of Laplace Equation we have: Incorporate derivative, gives A. After 2 nd integration of Laplace Equation we have: Incorporate constant head, gives B.

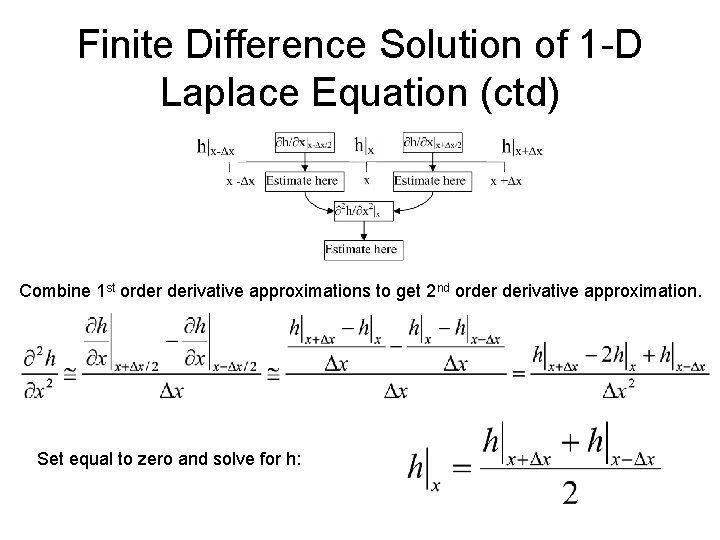
Finite Difference Solution of 1 -D Laplace Equation Need finite difference approximation for 2 nd order derivative. Start with 1 st order. Look the other direction and estimate at x – Dx/2:

Finite Difference Solution of 1 -D Laplace Equation (ctd) Combine 1 st order derivative approximations to get 2 nd order derivative approximation. Set equal to zero and solve for h:

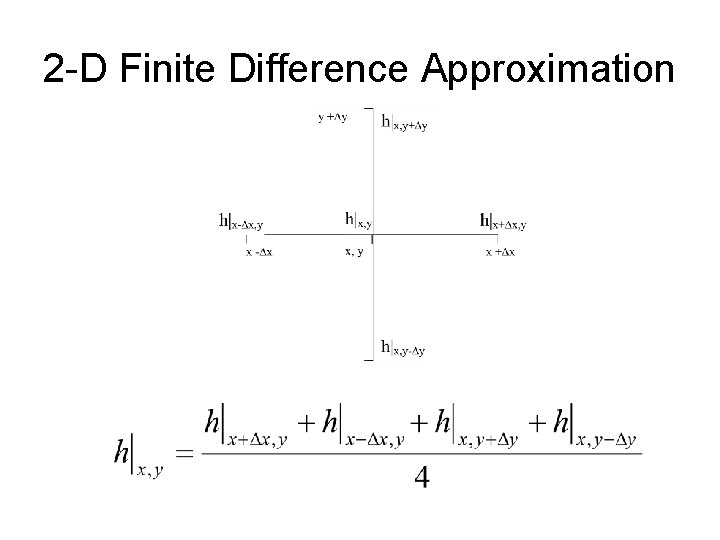
2 -D Finite Difference Approximation

Matrix Notation/Solutions • Ax=b • A-1 b=x

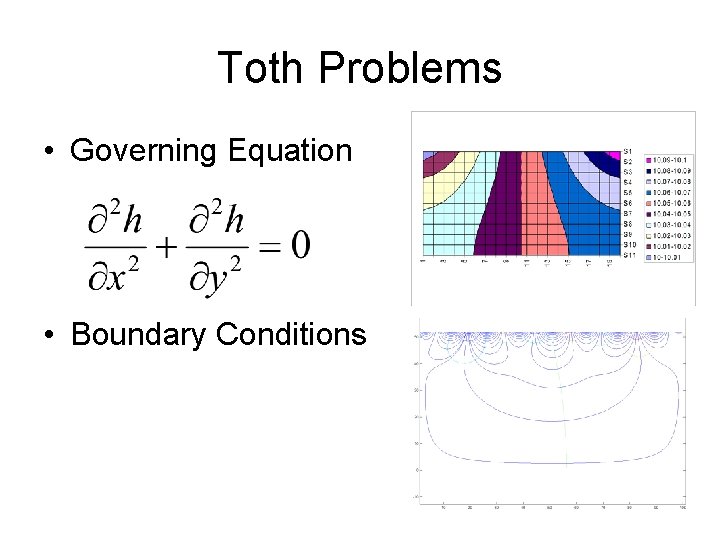
Toth Problems • Governing Equation • Boundary Conditions

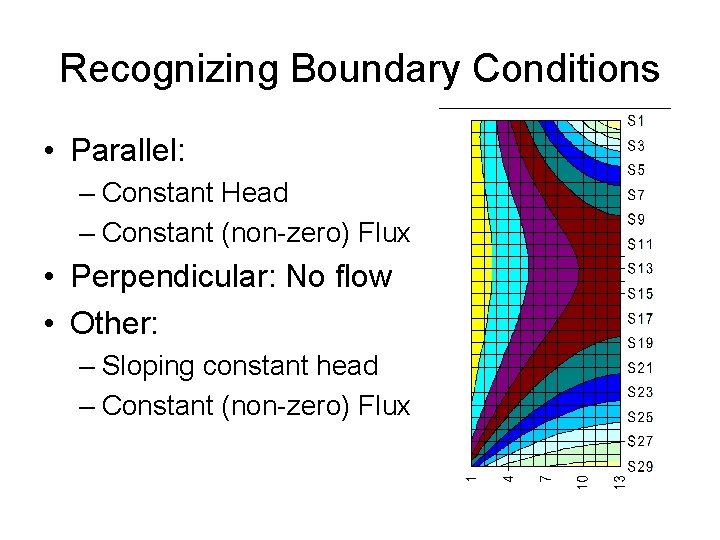
Recognizing Boundary Conditions • Parallel: – Constant Head – Constant (non-zero) Flux • Perpendicular: No flow • Other: – Sloping constant head – Constant (non-zero) Flux

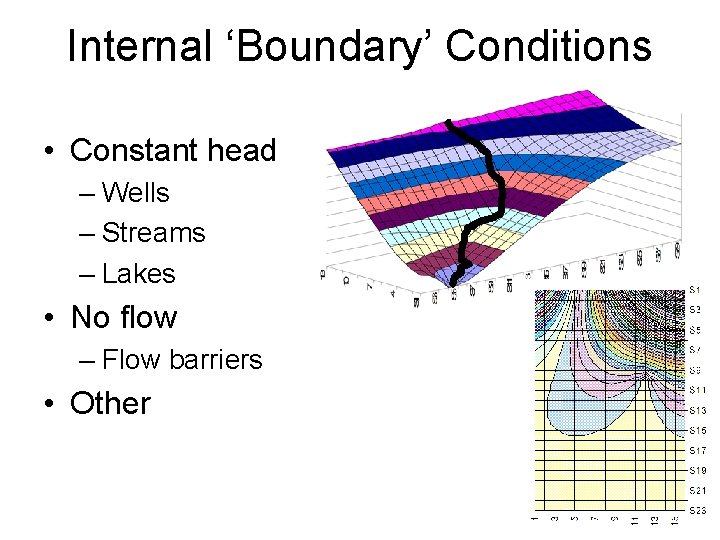
Internal ‘Boundary’ Conditions • Constant head – Wells – Streams – Lakes • No flow – Flow barriers • Other

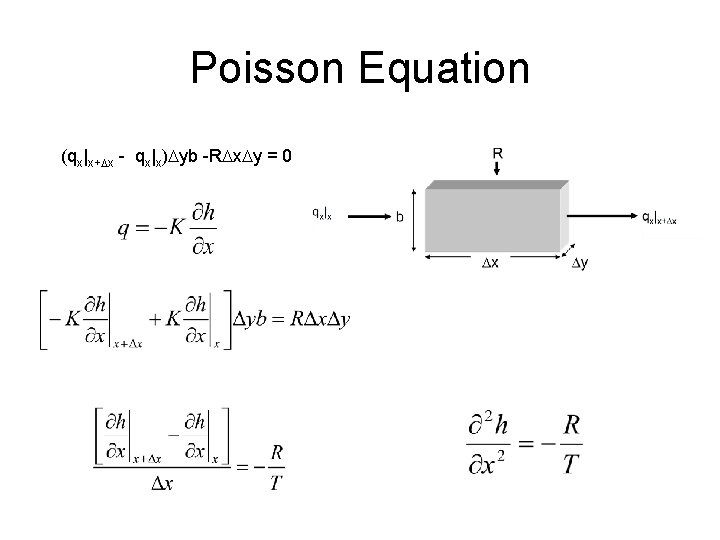
Poisson Equation • Add/remove water from system so that inflow and outflow are different • R can be recharge, ET, well pumping, etc. • R can be a function of space and time • Units of R: L T-1

Poisson Equation (qx|x+Dx - qx|x)Dyb -RDx. Dy = 0

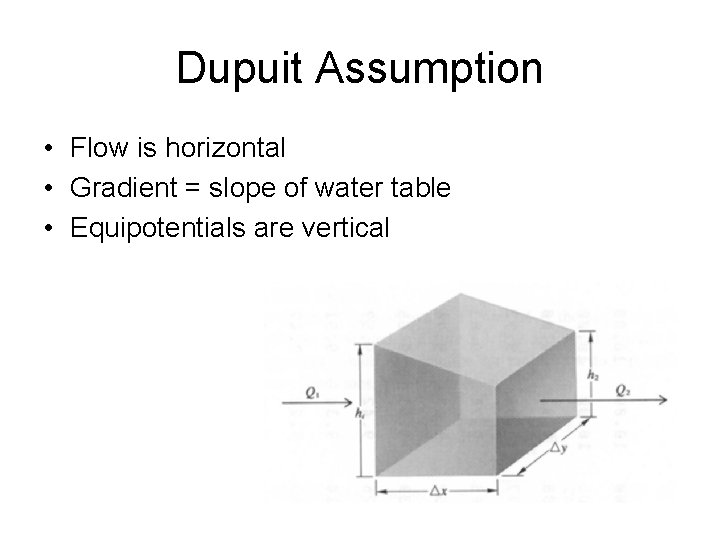
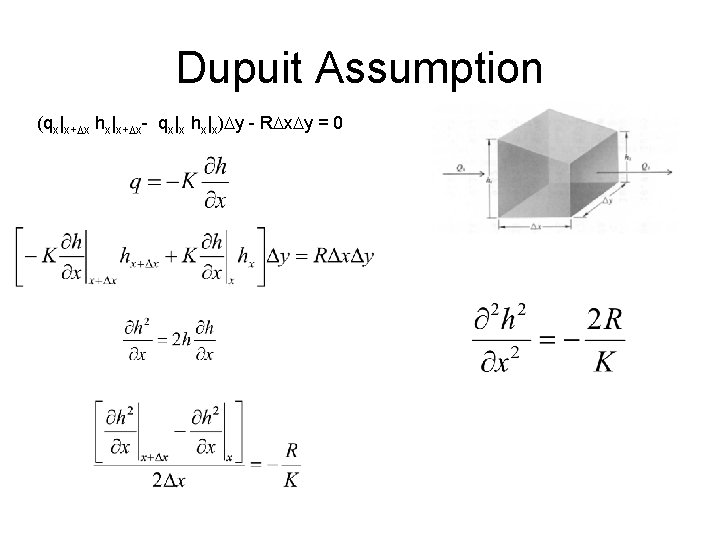
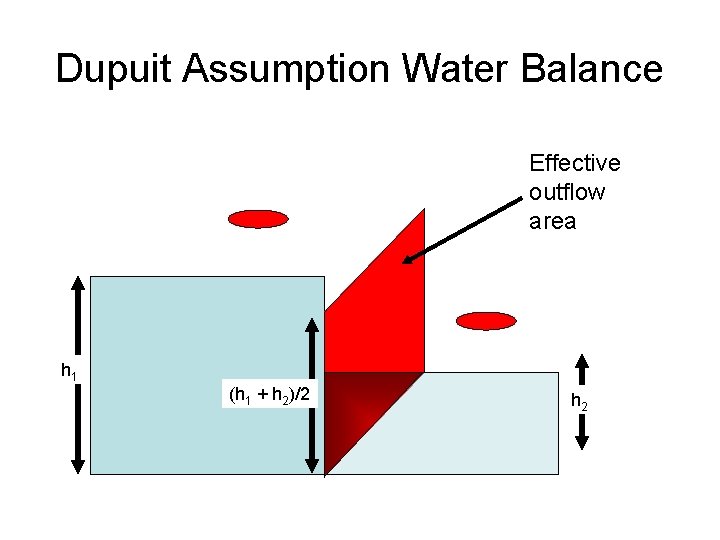
Dupuit Assumption • Flow is horizontal • Gradient = slope of water table • Equipotentials are vertical

Dupuit Assumption (qx|x+Dx hx|x+Dx- qx|x hx|x)Dy - RDx. Dy = 0

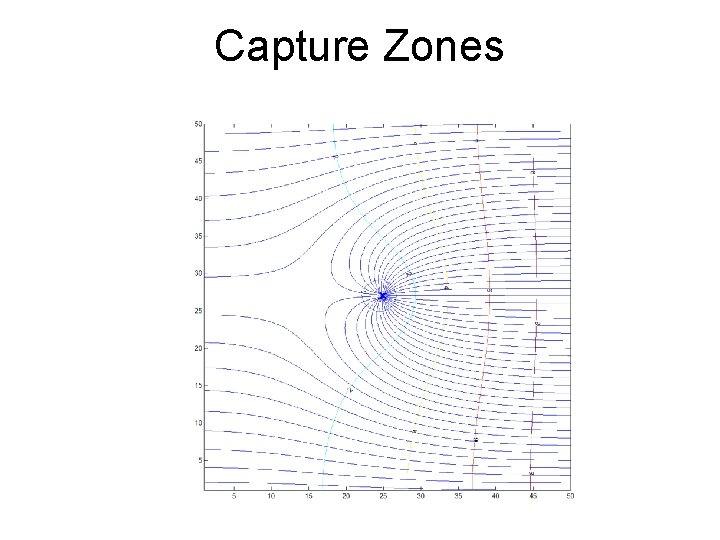
Capture Zones

Water Balance and Model Types

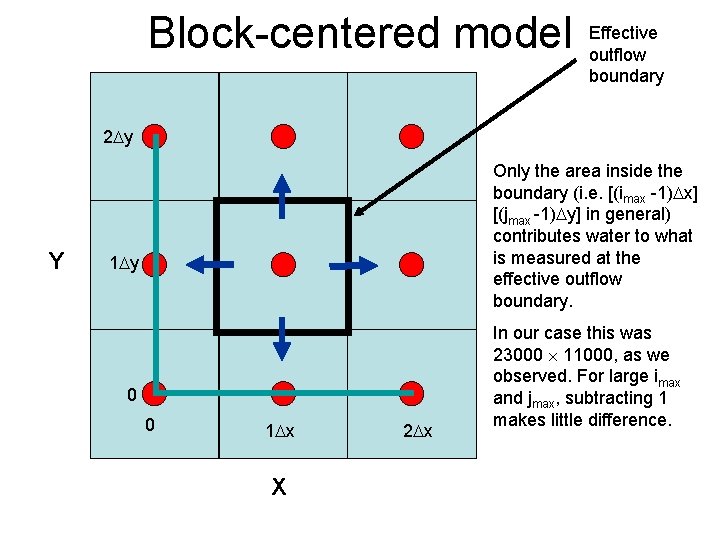
Block-centered model Effective outflow boundary 2 Dy Y Only the area inside the boundary (i. e. [(imax -1)Dx] [(jmax -1)Dy] in general) contributes water to what is measured at the effective outflow boundary. 1 Dy 0 0 1 Dx X 2 Dx In our case this was 23000 11000, as we observed. For large imax and jmax, subtracting 1 makes little difference.

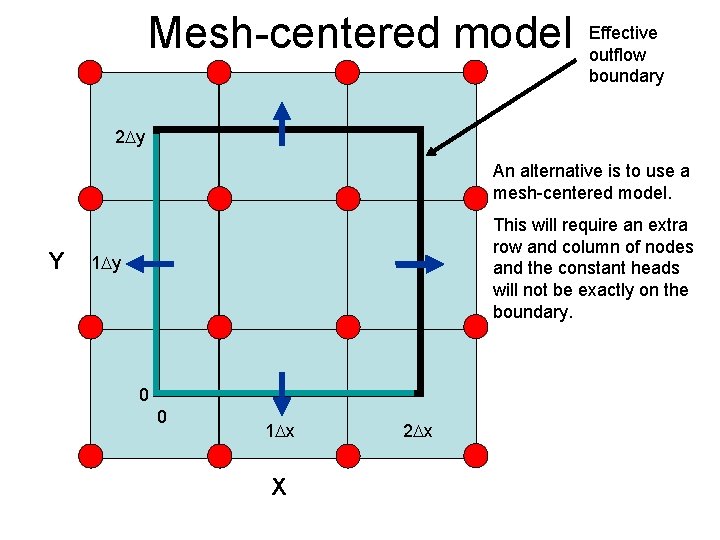
Mesh-centered model Effective outflow boundary 2 Dy An alternative is to use a mesh-centered model. Y This will require an extra row and column of nodes and the constant heads will not be exactly on the boundary. 1 Dy 0 0 1 Dx X 2 Dx

Summary • In summary, there are two possibilities: – Block-centered and – Mesh-centered. • Block-centered makes good sense for constant head boundaries because they fall right on the nodes, but the water balance will miss part of the domain. • Mesh-centered seems right for constant flux boundaries and gives a more intuitive water balance, but requires an extra row and column of nodes. • The difference between these models becomes negligible as the number of nodes becomes large.

Dupuit Assumption Water Balance Effective outflow area h 1 (h 1 + h 2)/2 h 2

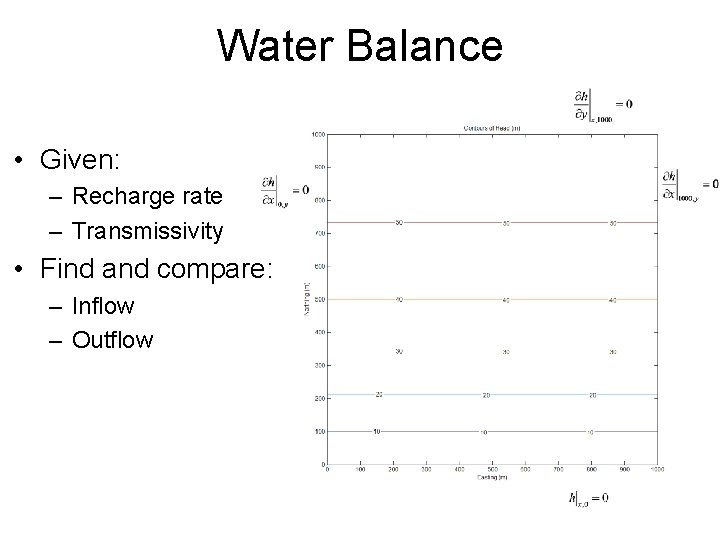
Water Balance • Given: – Recharge rate – Transmissivity • Find and compare: – Inflow – Outflow

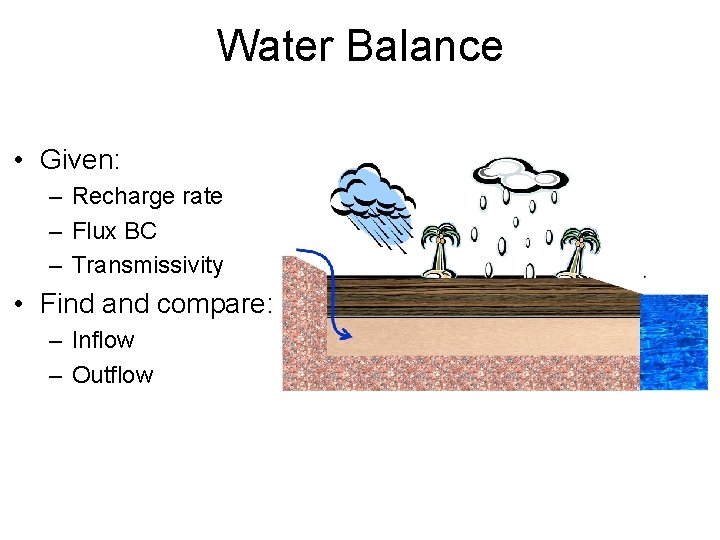
Water Balance • Given: – Recharge rate – Flux BC – Transmissivity • Find and compare: – Inflow – Outflow
 Fundamental theorem
Fundamental theorem Gradient operator
Gradient operator Michael britt brain mnemonics
Michael britt brain mnemonics Algebra 1 midterm exam
Algebra 1 midterm exam Whap midterm review
Whap midterm review Cows
Cows Global 9 midterm review
Global 9 midterm review Trig midterm review
Trig midterm review Chemistry midterm review
Chemistry midterm review Business law midterm answers
Business law midterm answers Apes midterm review
Apes midterm review Ap chemistry midterm
Ap chemistry midterm Algebra 2 midterm exam review answers
Algebra 2 midterm exam review answers Spanish 2 midterm review
Spanish 2 midterm review Mid term test english 10
Mid term test english 10 World history first semester exam review
World history first semester exam review Biology midterm review
Biology midterm review Geometry midterm exam
Geometry midterm exam Area of sector radians
Area of sector radians Derivative of tan
Derivative of tan Differentiation of tan inverse
Differentiation of tan inverse Calculus limits review
Calculus limits review Pre calculus unit 1 review
Pre calculus unit 1 review Jika sin 5 derajat = p
Jika sin 5 derajat = p Cos c -cos d
Cos c -cos d Sederhanakan 2 cos 15 sin 30 + 2 sin 25 sin 15
Sederhanakan 2 cos 15 sin 30 + 2 sin 25 sin 15 Sen(a+b)+sen(a-b)
Sen(a+b)+sen(a-b) Fabula testo narrativo
Fabula testo narrativo Il testo narrativo: schema
Il testo narrativo: schema Composition of inverse trig functions
Composition of inverse trig functions Nilai dari 6 sin 112,5 sin 22,5 adalah
Nilai dari 6 sin 112,5 sin 22,5 adalah Sin 270
Sin 270 Nlp midterm exam
Nlp midterm exam Data mining midterm exam with solutions
Data mining midterm exam with solutions Difference between html and xhtml
Difference between html and xhtml Mid term break images
Mid term break images Eku direct
Eku direct Midterm exam for applied research methods
Midterm exam for applied research methods Prelim midterm finals grading system
Prelim midterm finals grading system Nr 601 week 3 quiz
Nr 601 week 3 quiz Ics 111
Ics 111 Mid term thesis presentation
Mid term thesis presentation Mid term break poem analysis
Mid term break poem analysis Global history midterm
Global history midterm Biology practice midterm
Biology practice midterm English 9 midterm exam
English 9 midterm exam Computer science midterm
Computer science midterm Introduction to computer science midterm exam
Introduction to computer science midterm exam Introduction to computer science midterm exam test
Introduction to computer science midterm exam test Regents chemistry midterm
Regents chemistry midterm Ap english language and composition midterm exam
Ap english language and composition midterm exam What is a midterm
What is a midterm Grva midterm exam
Grva midterm exam To remember a list of the school supplies she needs
To remember a list of the school supplies she needs