METFLU UBH ZUHERNA MIZWAR zmizwaryahoo com 081388629937 Tugas

METFLU - UBH ZUHERNA MIZWAR zmizwar@yahoo. com 081388629937

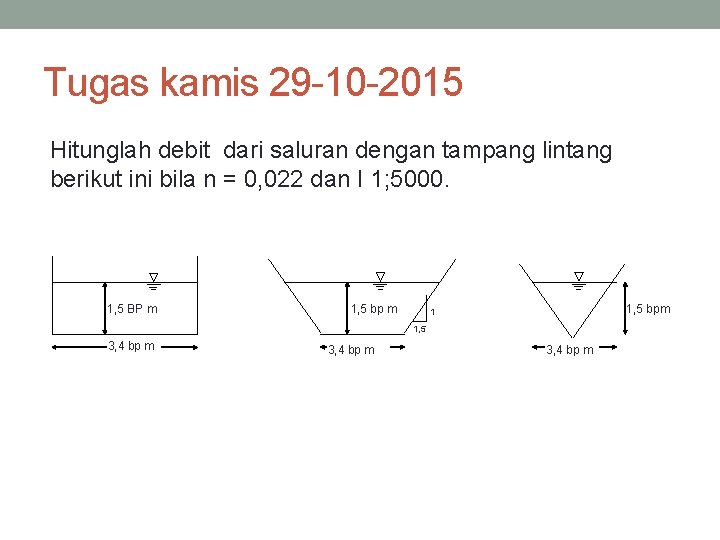
Tugas kamis 29 -10 -2015 Hitunglah debit dari saluran dengan tampang lintang berikut ini bila n = 0, 022 dan I 1; 5000. 1, 5 BP m 1, 5 bpm 1 1, 5 3, 4 bp m

Penyelesaian a) Luas tampang A = b h Keliling basah P = b + 2 h Jari-jari hidraulik R = A/P b) Luas tampang A = [B+(B+2 mh)]0, 5 h Keliling basah : P = B + 2 h Jari-jari hidraulis : R = A/P

ALIRAN FLUIDA DALAM PIPA v Pressure Drop v Aliran Fluida v Persamaan Kontinuitas v Persamaan Bernoulli v Karakteristik Aliran Di Dalam Saluran/Pipa v Karakteristik Aliran Melalui Sambungan- Sambungan

1 Pendahuluan q Sistem perpipaan adalah suatu sistem yang banyak digunakan untuk memindahkan fluida, baik cair, gas, maupun campuran cair dan gas dari suatu tempat ke tempat yang lain q Sistem perpipaan yang lengkap terdiri atas : Ø Pipa Ø Sambungan-Sambungan (fitting) Ø Peralatan pipa (pompa) Ø dll

2 Pressure Drop § Terjadi akibat aliran fluida mengalami gesekan dengan permukaan saluran § Dapat juga terjadi ketika aliran melewati sambungan pipa, belokan, katup, difusor, dan sebagainya § Besar Pressure Drop bergantung pada : * Kecepatan aliran * Kekasaran permukaan * Panjang pipa * Diameter pipa

3 Aliran Fluida Jenis Aliran Fluida : q. Steady atau tidak steady q. Laminar atau Turbulen q. Satu, dua, atau tiga dimensi ü Steady jika kecepatan aliran tidak merupakan fungsi waktu ( dv/dt = 0) ü Aliran laminer atau turbulen tergantung dari bilangan Reynolds ü Aliran satu dimensi terjadi jika arah dan besar kecepatan di semua titik sama ü Aliran dua dimensi terjadi jika fluida mengalir pada sebuah bidang (sejajar suatu bidang) dan pola garis aliran sama untuk semua bidang

• Garis arus adalah kurva imajinasi yang digambar mengikuti pergerakan fluida untuk menunjukan arah pergerakan aliran fluida tersebut • Vektor kecepatan pada setiap titik kurva : • Tidak memiliki arah normal • Tidak akan ada aliran yang berpindah dari suatu garis arus ke garis arus lain Gambar garis arus dan vektor kecepatan

4 Persamaan Kontinuitas Persamaan kontinuitas diperoleh dari hukum kekekalan massa yaitu: Diman a Fluida incompressibel Massa jenis fluida Luas penampang aliran Kecepatan aliran Catatan : Bidang A dan V harus tegak lurus satu sama lainnya

Contoh 1. Jika kecepatan alir pada pipa berdiameter 12 cm adalah 0, 5 m/s, berapa kecepatan aliran tersebut jika pipa dikecilkan menjadi 3 cm?

4. 5 Persamaan Bernoulli ØMerupakan salah satu bentuk penerapan hukum kekekalan energi ØPrinsipnya adalah energi pada dua titik yang dianalisis haruslah sama ØUntuk aliran steady dan fluida incompressibel (perubahan energi dalam diabaikan) persamaan yang diperoleh adalah : Dimana: Z = ketinggian HL= head loss dari titik 1 ke titik 2

Contoh 2 Gambar di bawah menunjukkan aliran air dari titik A ke titik B dengan debit aliran sebesar 0, 4 m 3/s dan head tekanan pada titik A = 7 m. Jika diasumsikan tidak ada losses antara titik A dan titik B, tentukan head tekanan di titik B Penyelesaian:

4. 6 Karakteristik Aliran Di Dalam Saluran/Pipa v. Aliran di dalam suatu saluran selalu disertai dengan friksi v. Aliran yang terlalu cepat akan menimbulkan pressure drop yang tinggi sedangkan aliran yang terlalu lambat pressure drop-nya akan rendah akan tetapi tidak efisien v. Kecepatan aliran perlu dibatasi dengan memperhatikan : * Besarnya daya yang dibutuhkan * Masalah erosi pada dinding pipa * Masalah pembentukan deposit/endapan * Tingkat kebisingan yang terjadi

Harga-harga kecepatan aliran air yang dianjurkan untuk berbagai pemakaian Service Daerah kecepatan (fps) Keluaran pompa 8 -12 Pipa isap pompa 4 -7 Saluran pembuangan 4 -7 Header 4 -15 Riser 3 -10 Service umum 5 -10 Air minum 3 -7

Kecepatan maksimum aliran fluida dalam pipa Jenis fluida Kecepatan maksimum [ft/s] Uap untuk proses 120 150 Slurry 5 10 Uap air 100 130 Air 6 10 Fluida cair 100/ 1/2

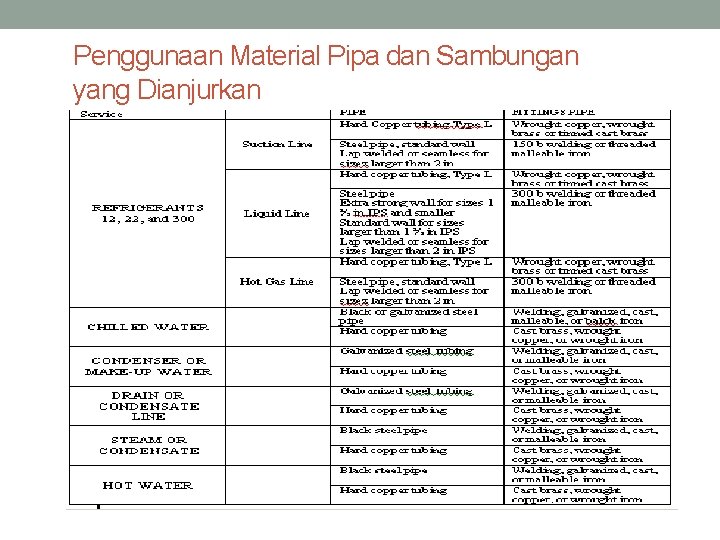
Penggunaan Material Pipa dan Sambungan yang Dianjurkan

Kerugian yang terdapat di dalam aliran fluida § Kerugian tekanan (Pressure Drop) atau § Kerugian head ( Head Loss) Faktor yang mempengaruhi kerugian di dalam aliran fluida: üKecepatan aliran üLuas penampang saluran üFaktor friksi üViskositas üDensitas fluida

Persamaan matematis kerugian tekanan di dalam saluran sirkuler Dimana : P = kerugian tekanan Hubungan antara head dan tekanan : d = diameter pipa V = kecepatan aliran f = faktor friksi Kerugian head (head loss) : l = panjang pipa g = grafitasi h = head Catatan: harga f untuk pipa-pipa tertentu dapat dicari dengan menggunakan diagram Moody dengan terlebih dahulu menghitung bilangan Reynolds

Kerugian head dengan menggunakan konstanta K sebagai pengganti faktor friksi Kerugian tekanan dengan menggunakan konstanta K sebagai pengganti faktor friksi Catatan : Kerugian aliran akan semakin besar jika kecepatan aliran semakin cepat dan saluran semakin panjang

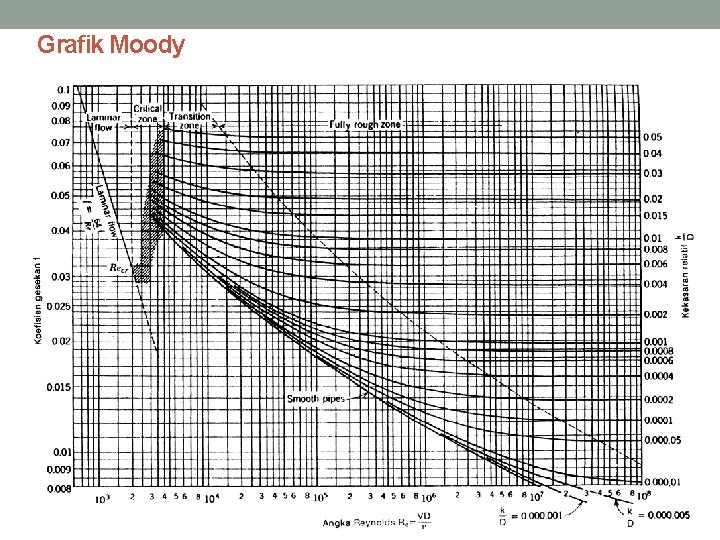
Grafik Moody

Grafik Kerugian Head untuk Sistem Pipa Tertutup

Grafik Kerugian Head untuk Sistem Pipa Terbuka

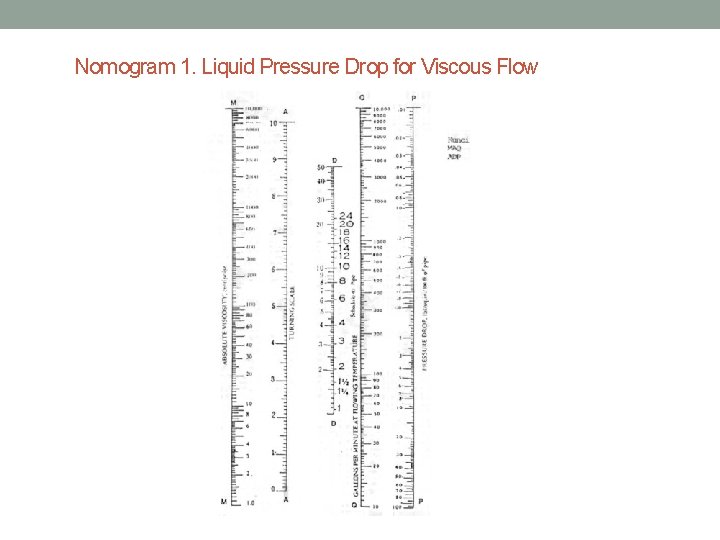
Nomogram 1. Liquid Pressure Drop for Viscous Flow

4. 7 Karakteristik Aliran Melalui Sambungan-Sambungan Bentuk-bentuk sambungan pada sistem perpipaan: v. Sambungan lurus v. Sambungan belok v. Sambungan cabang v. Sambungan dengan perubahan ukuran saluran Cara-cara penyambungan pada sistem pemipaan: üUlir üPress üFlens üLem üLas

Persamaan matematis kerugian akibat sambungan (kerugian minor) dalam sistem pemipaan: Keterangan: K = Koefisien hambatan minor

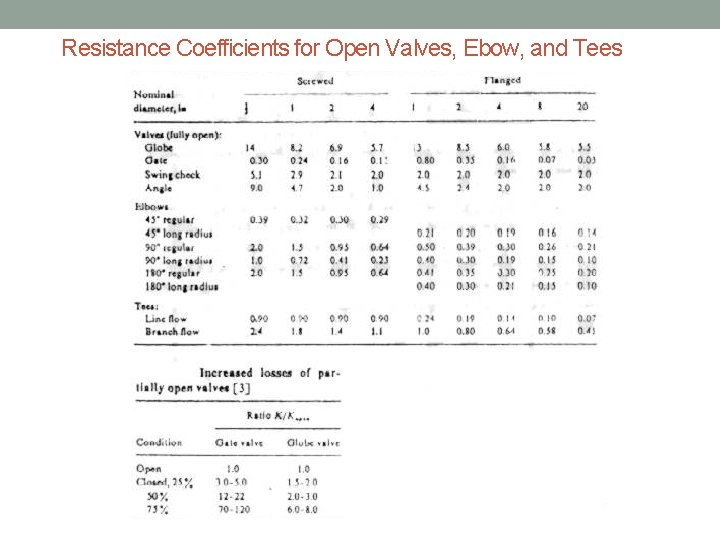
Resistance Coefficients for Open Valves, Ebow, and Tees

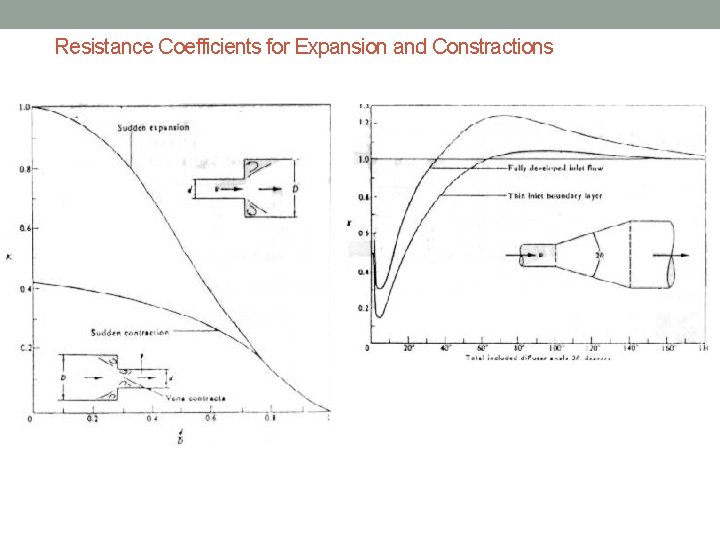
Resistance Coefficients for Expansion and Constractions

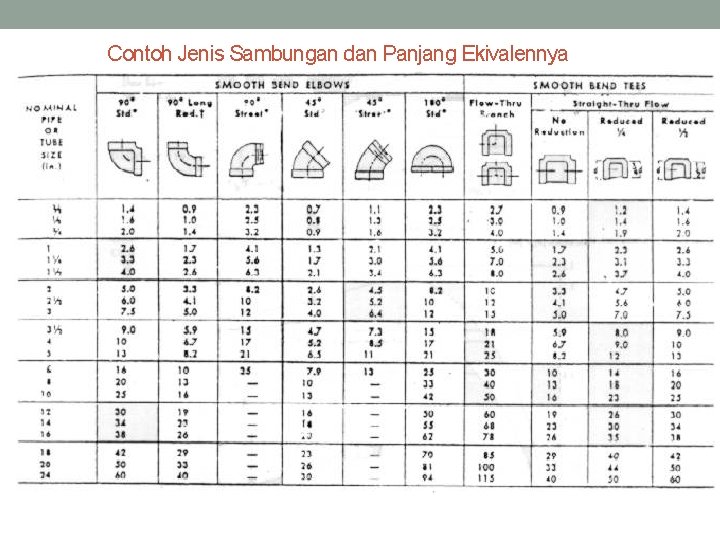
Contoh Jenis Sambungan dan Panjang Ekivalennya

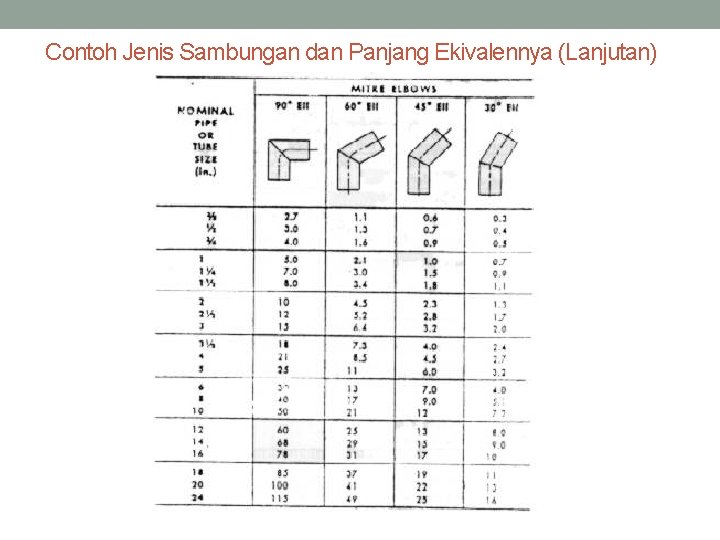
Contoh Jenis Sambungan dan Panjang Ekivalennya (Lanjutan)

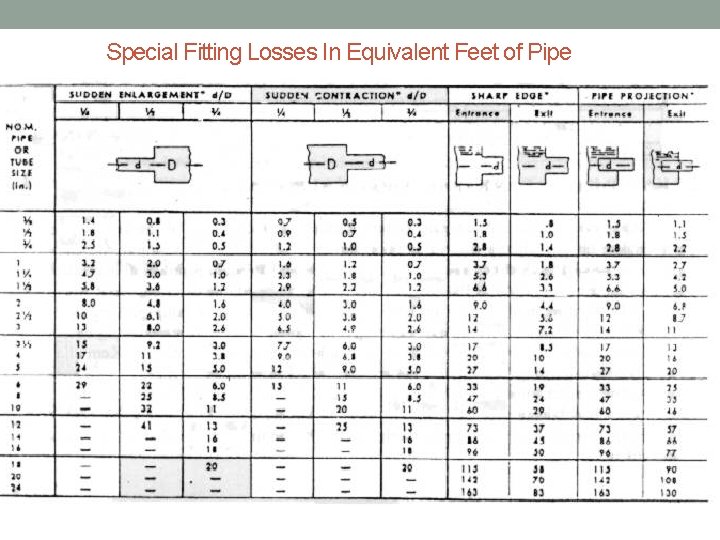
Special Fitting Losses In Equivalent Feet of Pipe

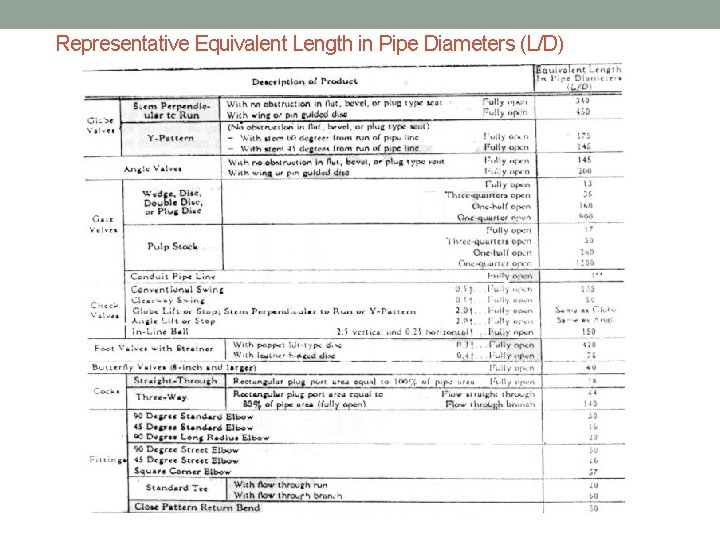
Representative Equivalent Length in Pipe Diameters (L/D)

4. 8 Beberapa Contoh Perhitungan Karakteristik Aliran Sistem Di Dalam Sistem Pemipaan Contoh 1. Suatu sistem pemipaan terdiri dari komponen seperti gambar. Air mengalir dengan kecepatan sebesar 9, 7 fps dan diameter 6 inch. Pipa tersebut adalah pipa baru dengan panjang 1200 ft. Katup gerbang berada posisi terbuka penuh. Tentukan kerugian tekanan dari titik 1 hingga titik 3.

Penyelesaian: Kerugian aliran dari titik 1 s. d 3 adalah jumlah dari kerugian-kerugian aliran pada pengecilan penampang di titik 1, kerugian friksi sepanjang pipa 1 s. d 2 dan kerugian pada katup. Dari grafik resistance coefficient for expantion and constraction diperoleh harga K= 0, 42 untuk titik 1, sehingga kerugiannya: Aliran yang terjadi adalah turbulen. Jika kekasaran pipa 0, 0017 maka dengan mengunakan diagram Moody diperoleh f = 0, 023

PIPA • Pipa adalah saluran tertutup yang biasanya berpenampang lingkaran digunakan untuk mengalirkan fluida dengan tampang aliran penuh. • Apabila zat cair di dalam pipa tidak penuh maka aliran termasuk jenis aliran saluran terbuka.

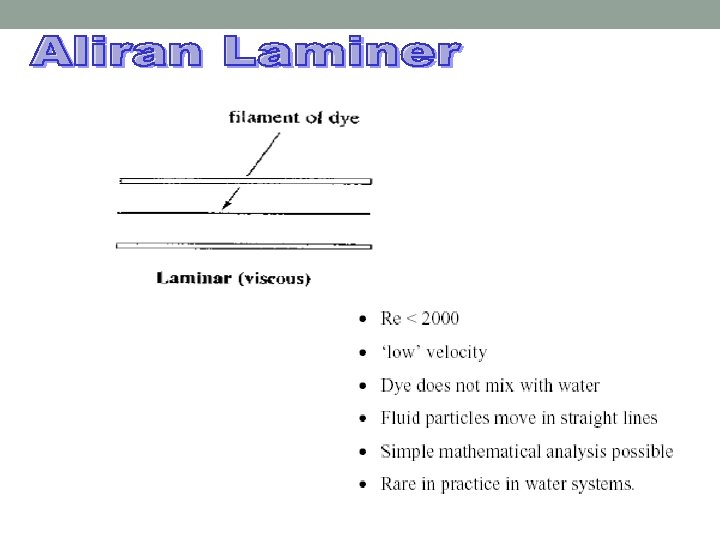
KEHILANGAN TENAGA • Fluida yang mengalir melalui pipa dapat berupa zat cair atau gas. Sedangkan jenis aliran yang terjadi dapat laminer atau turbulen. Aliran zat cair riil yang melalui pipa selalu disertai kehilangan tenaga searah dengan aliran

Angka Reynolds mempunyai bentuk: Dengan: V : kecepatan aliran D : diameter pipa v : kekentalan kinematik

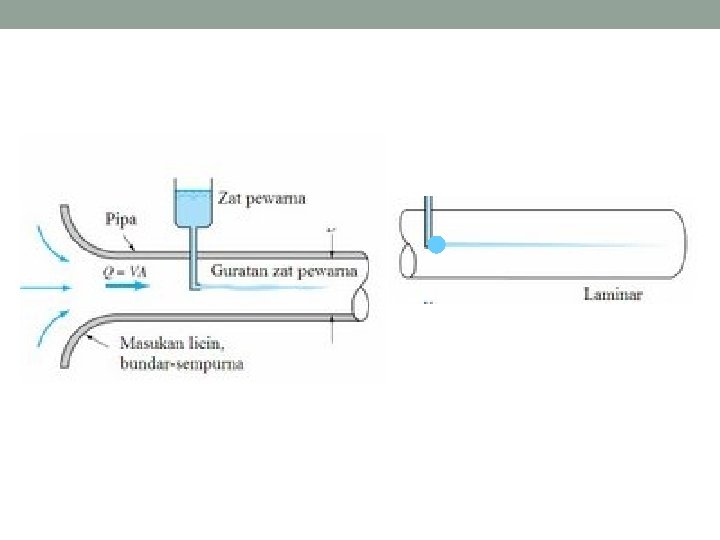
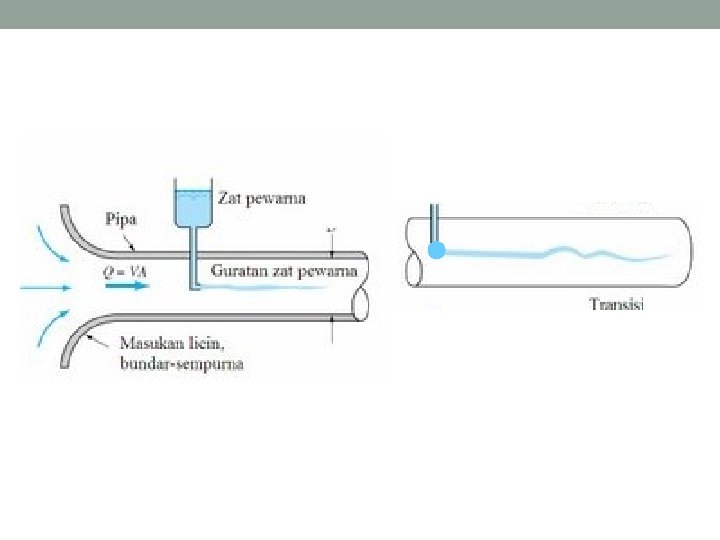
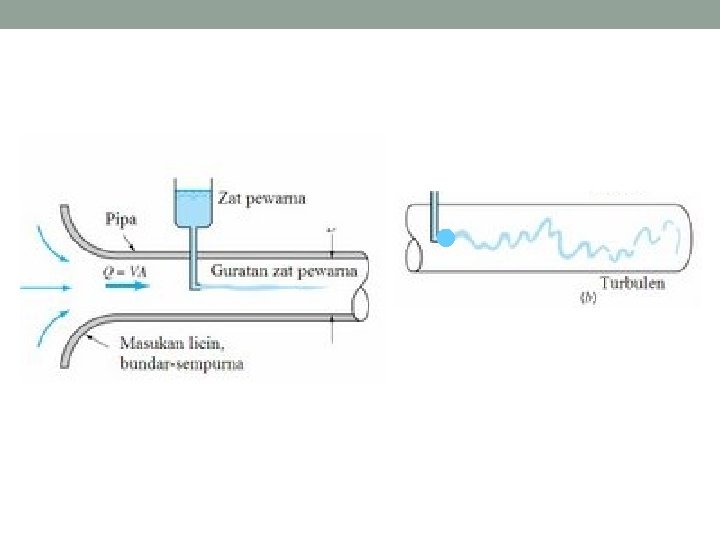
• Besarnya angka Reynolds dapat menunjukkan jenis aliran. Re < 2000 → aliran laminer 2000 < Re < 4000 → aliran transisi Re > 4000 → aliran turbulen

Soal • Air mengalir melalui pipa berdiameter 150 mm dan kecepatan 5, 5 m/d. Kekentalan kinematik air adalah 1, 3 x 10 -6 m 2/d. Selidiki tipe aliran!

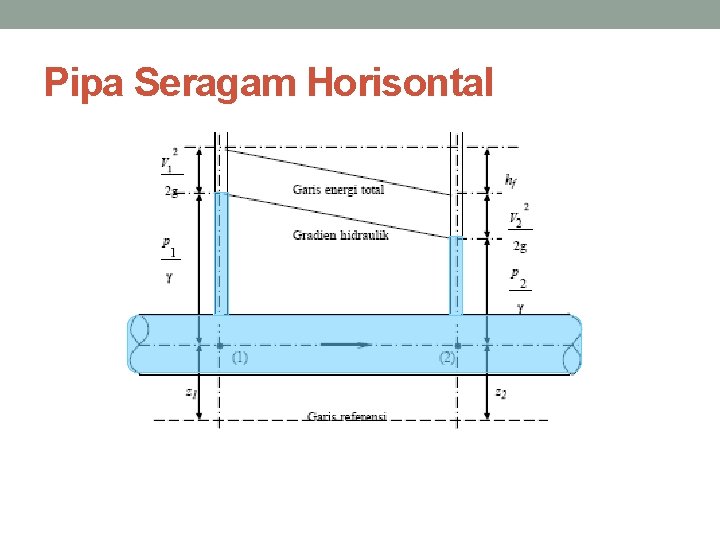
Pipa Seragam Horisontal

• Persamaan Bernoulli untuk titik 1 dan 2 pada gambar di atas adalah sebagai berikut : dengan z : elevasi (tinggi tempat); : tinggi tekanan; : tinggi kecepatan. Bila pipa terletak horisontal, tampang lintang seragam dan tampang aliran penuh maka z 1 = z 2 dan v 1 = v 2 sehingga : dengan hf adalah kehilangan tenaga.

• Pada kondisi lain, dimana tampang lintang tidak seragam dan ada perbedaan tinggi tempat (pipa tidak terpasang horisontal) maka persamaan Bernoulli untuk titik 1 dan 2 pada gambar di bawah adalah sebagai berikut :

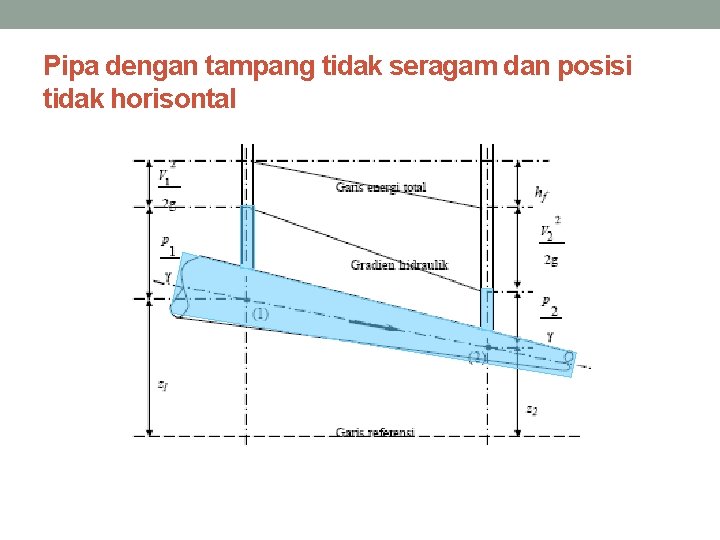
Pipa dengan tampang tidak seragam dan posisi tidak horisontal

Kehilangan tenaga pada aliran laminer • Pada aliran laminer, kehilangan tenaga terutama disebabkan oleh adanya kekentalan fluida dan tidak dipengaruhi oleh bidang batas atau kekasaran dinding, seperti ditunjukkan oleh persamaan Poiseuille sebagai berikut : • dengan ν V L g D : kekentalan kinematik : kecepatan aliran; : panjang pipa; : percepatan gravitasi; : diameter pipa.

Kehilangan tenaga pada aliran turbulen • Pada aliran turbulen melalui pipa, kehilangan tenaga berhubungan dengan tegangan akibat tahanan gesek dari dinding pipa. Pada tahun 1850 Darcy dan Weisbach mengemukakan sebuah persamaan yang dikenal sebagai persamaan Darcy -Weisbach untuk kehilangan tenaga dalam pipa. • dengan f : koefisien gesekan Darcy-Weisbach

Koefisien gesek • Pada persamaan di atas, f adalah koefisien gesekan Darcy- Weisbach yang tidak berdimensi. Koefisien f merupakan fungsi dari angka Reynolds dan kekasaran pipa. Untuk aliran laminer koefisien gesekan hanya dipengaruhi oleh angka Reynolds dan mempunyai bentuk : • Harga f tersebut diperoleh dari persamaan Poiseuille yang ditulis dalam bentuk persamaan Darcy-Weisbach. Pada aliran turbulen, pipa dapat bersifat hidraulis halus atau hidraulis kasar. Untuk pipa halus, Blasius mengemukakan rumus gesekan f dalam bentuk : • Rumus tersebut berlaku untuk 4000<Re<105

• Dalam praktek, pipa yang digunakan kebanyakan tidak halus tetapi mempunyai kekasaran dinding. Tahanan pada pipa kasar lebih besar daripada pipa halus. • Untuk pipa kasar nilai f tidak hanya tergantung pada angka Reynolds tetapi juga pada sifat dinding pipa yaitu kekasaran k/D atau : • Pada tahun 1944, Moody mengemukakan suatu grafik yang memberi gambaran f tergantung angka Reynolds (Re) dan kekasaran relatif (k/D ). Grafik tersebut dikenal sebagai grafik Moody (Gambar di bawah).

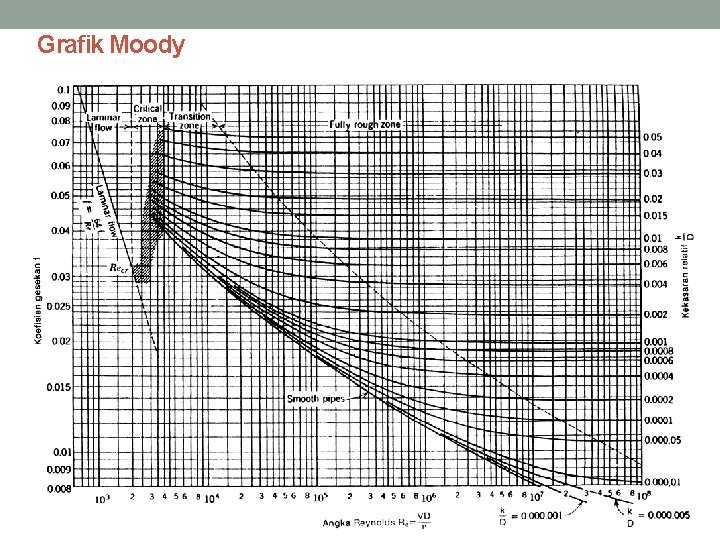
Grafik Moody

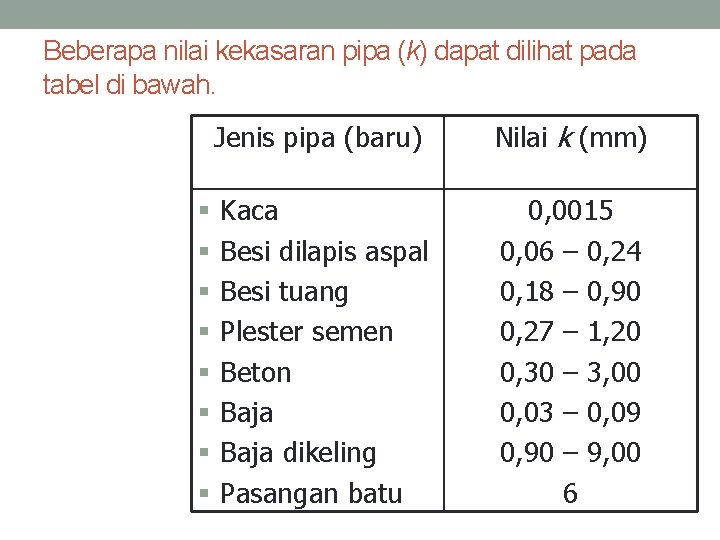
Beberapa nilai kekasaran pipa (k) dapat dilihat pada tabel di bawah. § § § § Jenis pipa (baru) Nilai k (mm) Kaca Besi dilapis aspal Besi tuang Plester semen Beton Baja dikeling Pasangan batu 0, 0015 0, 06 – 0, 24 0, 18 – 0, 90 0, 27 – 1, 20 0, 30 – 3, 00 0, 03 – 0, 09 0, 90 – 9, 00 6

• Grafik Moody juga dapat dinyatakan dengan persamaan yang dikemukakan oleh Swamee dan Jain (1976) yang mempunyai bentuk : • Persamaan di atas berlaku untuk rentang 5∙ 103 < Re < 106 dan 10 -6 < k/D < 10 -2

Soal 1. Hitung kehilangan tenaga karena gesekan di dalam pipa sepanjang 1500 m dan diameter 20 cm, apabila air mengalir dengan kecepatan 2 m/d. Koefisien gesekan f = 0, 02. Air mengalir melalui pipa berdiameter 15 cm dengan debit aliran 20 liter/detik. Apabila panjang pipa 2 km, hitung kehilangan tenaga di sepanjang pipa jika koefisien gesekan Darcy-Weisbach f = 0, 015.

Penyelesaian Soal 1 Kehilangan tenaga Soal 2 Kecepatan aliran Kehilangan tenaga

Soal • Air mengalir di dalam pipa berdiameter 75 mm dan pada angka Reynolds 80. 000. Jika tinggi kekasaran k = 0, 15 mm, berapakah koefisien kekasaran pipa tersebut? Tentukan dengan Grafik Moody dan Rumus Swamee-Jain. Bandingkan hasilnya.

Penyelesaian Diketahui Re = 80. 000 dan Dengan menggunakan grafik Moody untuk nilai Re dan k/D tersebut akan didapat nilai f = 0, 0256

Dengan rumus

Air mengalir melalui pipa berdiameter 30 cm. Kehilangan tenaga tiap 1000 m adalah 5 m. Tinggi kekasaran pipa k = 0, 15 mm. Kekentalan kinematik air u = 0, 98. 10 -6 m 2/d. Hitung debit aliran!

Rumus-rumus Empiris untuk Kecepatan Aliran dalam Pipa • Kecepatan V dan debit aliran Q merupakan faktor yang penting dalam studi hidraulika. Dalam hitungan praktis, rumus yang banyak digunakan adalah persamaan kontinuitas, Q=A. V, dengan A adalah tampang aliran. Apabila kecepatan dan tampang aliran diketahui, maka debit aliran dapat dihitung. Demikian pula jika kecepatan debit aliran diketahui maka dapat dihitung luas tampang aliran yang diperlukan untuk melewatkan debit tersebut.

• Rumus -rumus empiris kecepatan aliran dikembangkan untuk memudahkan hitungan. Dalam rumus-rumus ini I adalah kemiringan garis tenaga (I = h/L). Untuk pipa halus, rumus Blasius dapat digunakan untuk nilai angka Reynolds 4000< Re<105, yang dapat ditunjukkan dalam bentuk :

• Untuk pipa di daerah transisi berlaku rumus Hazen • William yang berbentuk: • • • Nilai CH tergantung pada kekasaran yang dipengaruhi oleh jenis dan bahan pipa. Untuk pipa di daerah turbulen rumus Manning dapat digunakan. Rumus Manning biasa dipakai pada pengaliran di saluran terbuka, yang mempunyai bentuk : • dengan R adalah jari-jari hidraulis (R=D/4 untuk pipa • lingkaran) dan n adalah koefisien kekasaran Manning • yang berbeda-beda untuk tiap bahan pipa.

• Rumus Chezy dan Strickler juga sering digunakan. Bentuk rumus Chezy adalah : • Sedangkan rumus Strickler mempunyai bentuk : • Dengan ks adalah koefisien kekasaran Strickler (ks=1/n).

Koefisien Hazen-William

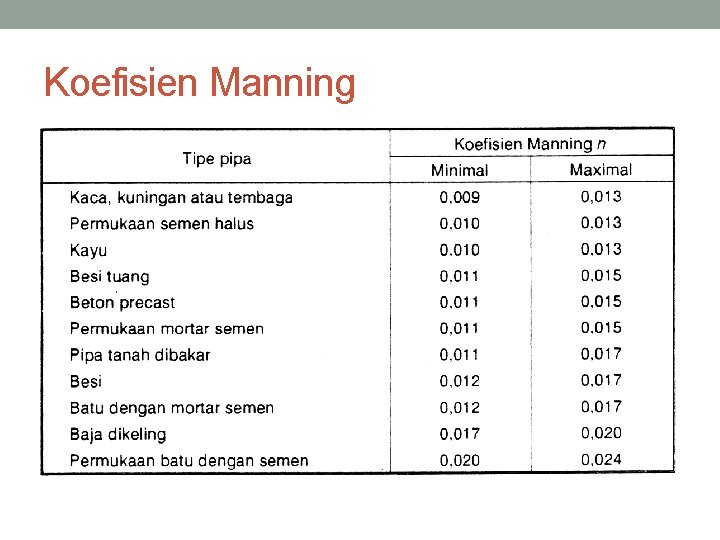
Koefisien Manning

Soal Dengan rumus Hazen-William tentukan kecepatan aliran yang terjadi jika aliran melewati pipa berdiameter 30 cm dan kemiringan garis tenaga 0, 002. Koefisien Hazen-William = 100. 2. Dengan rumus Manning tentukan kecepatan aliran yang terjadi jika aliran melewati pipa besi berdiameter 30 cm dan kemiringan garis tenaga 0, 001. Tentukan nilai koefisien Manning dari tabel. 1.

Penyelesaian Soal 1 Soal 2