MATA KULIAH KALKULUS I 4 sks Dosen Ir
















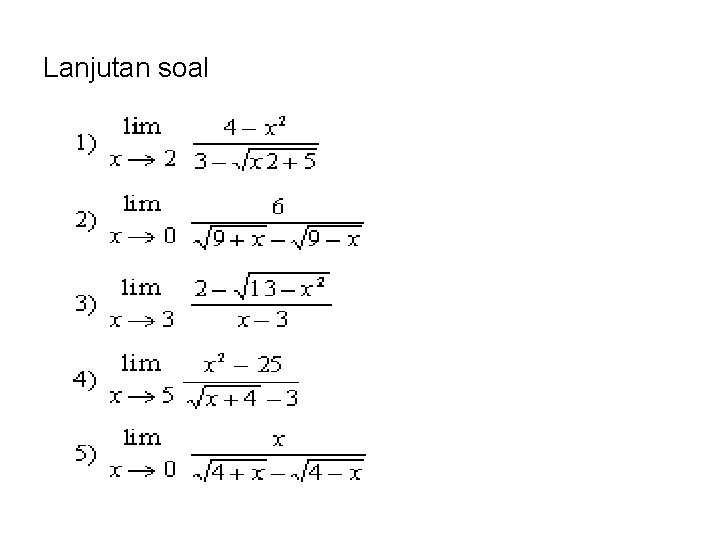




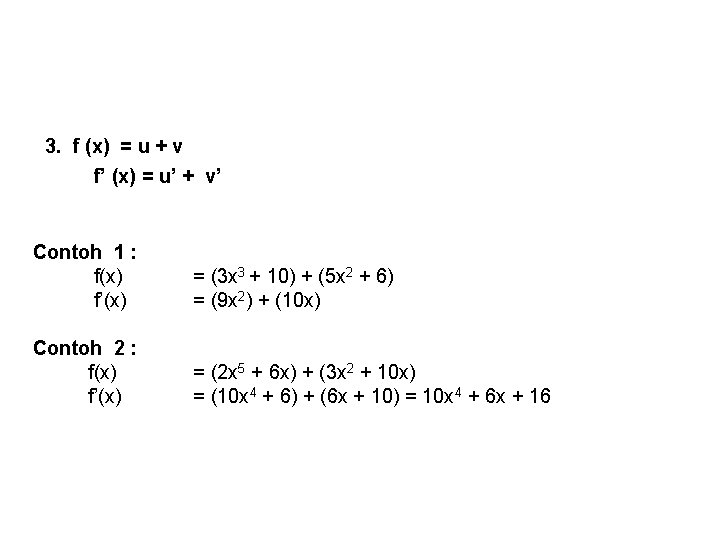



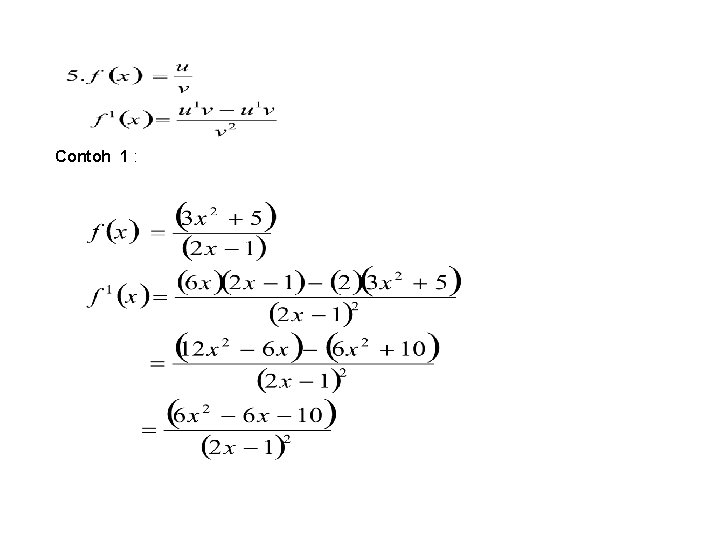
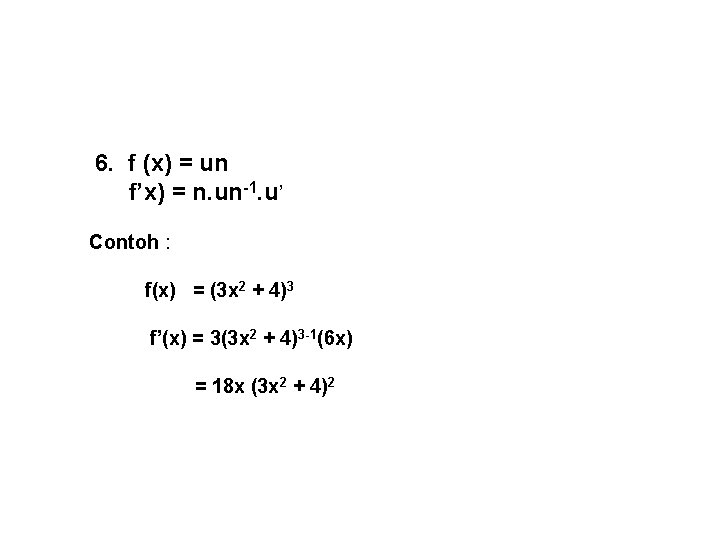
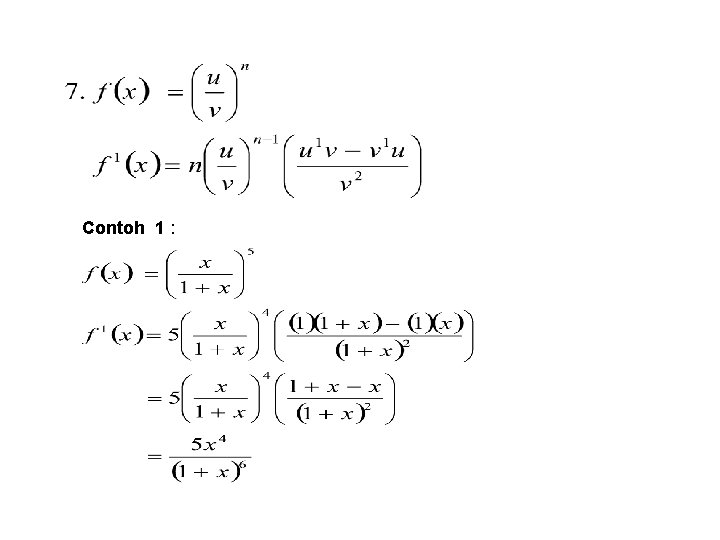























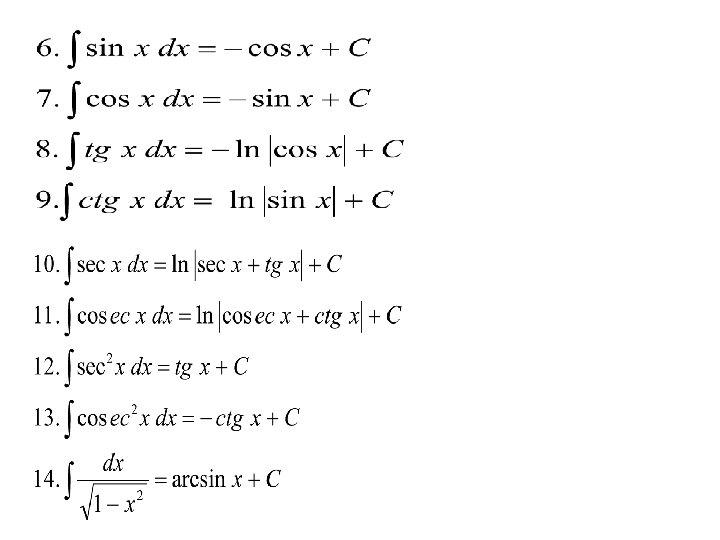





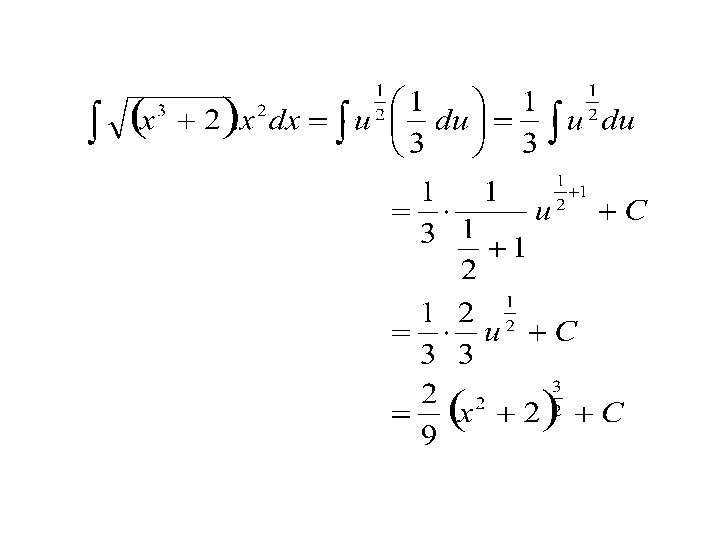


















- Slides: 77

MATA KULIAH KALKULUS I (4 sks) Dosen : Ir. RENILAILI, MT

Pertemuan ke 1 sistem bilangan

Sistem bilangan • Bilangan merupakan angka mulai dari 0 sampai 10 , tetapi bisa juga bilangan itu berupa pernyataan , seperti bilangan biner , bilangan decimal, bilangan ekponen , bilangan irrasional, bilangan imaginer dll.

Bilangan dasar 10 • 2763 = 2. 10 • 2783 = 2. 10 3 +7. 10 2+ 8. 10 1+3. 10 0 • • 3896, 475 = 3. 10 3 +8. 10 2 + 9. 10. 1 +6. 10 0 + 4. 10 -1 + 7. 10 + 5. 10 -3 -2

Pertemuan ke dua latihan soal-soal

Latihan soal • Latihan untuk merubah ke bilangan biner • Soal-soal: 2789 = 4789 = 9765 = 7569 = 6754 =

Pertemuan ketiga merubah basis

Merubah basis • Cara merubah basis dapat dilakukan dengan jalan membagi bilangan tersebut secara terus menerus sampai bilangan tersebut menghsilkan bilangan 0 • Contoh • 524 = 1014 8 • 897 = 629 12 • 0, 526 = 0, 4152 8

Pertemuan ke empat limit

LIMIT Difinisi : f (x) dikatakan mempunyai limit L untuk x → x 0, bila untuk setiap bilangan positif h yang diberikan, dapat ditunjuk bilangan positif δ sedemikian hingga untuk semua harga x yang memenuhi

TEOREMA LIMIT Teorema Limit • • • Jika K suatu konstanta, f dan g adalah fungsi – fungsi yang mempunyai limit untuk x → a, a ε R. f (x) = k → lim f (x) = k x→a f (x) = k → lim f (x) = a x→a Lim [ f(x) + g (x) ] = lim f(x) + lim g (x) x→a x→a Lim [ f(x) – g (x)] = lim f(x) – lim g (x) x→a x→a Lim k f(x) = K. lim f(x) x→a

1. Lim [ f(x). g (x) = lim f(x). lim g (x) x→a x→a 2. Lim = x→a 3. Lim [ f(x) ]n = [lim f(x)]n , n bilangan bulat x→a 4. Lim , n bilangan asli n ≥ 2 = x→a 5. Lim [ f(x)]m/n = x→a , m bilangan bulat lim f(x) ε R = x→a

Contoh-contoh penyelesaian limit


Pertemuan ke lima latihan soal-soal limit

Soal-soal latihan
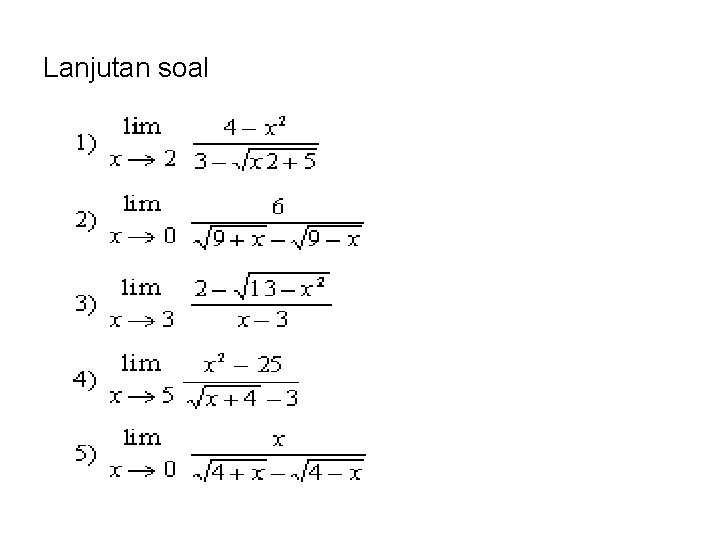
Lanjutan soal

Pertemuan ke enam differensial

DIFFERENSIAL Fungsi Aljabar f (x) difefenisikan sebagai fungsi x, dapat ditulis dengan singkat sebagai y dan f’ (x) merupakan turunan dari f (x) juga dalam hal ini dapat ditulis dengan dy/dx, tetapi ada fungsi-fungsi lainnya yang dalam buku ini ditulis sebagai u dan v yang digunakan untuk memperpendek cara penulisan.

RUMUS-RUMUS DASAR 1. f (x) = xn f’ (x) = n. xn-1 Contoh f (x) = x 5 f’ (x) = 5. x 4 f (x) = 2 x 3 f’ (x) = 6 x 2

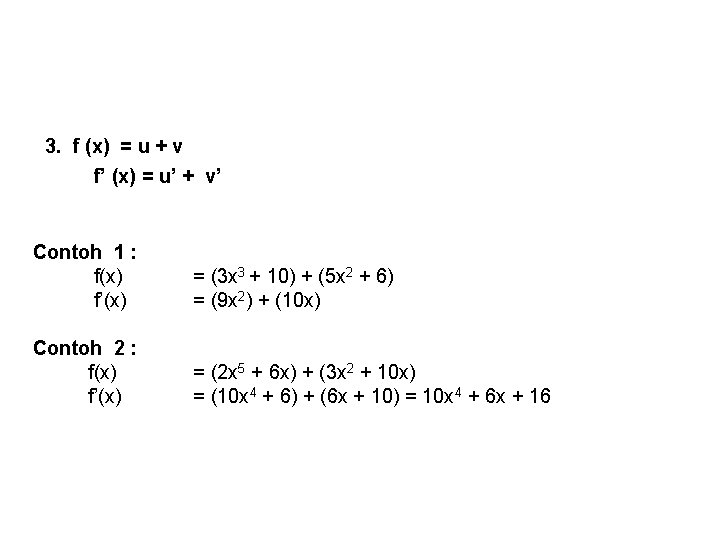
3. f (x) = u + v f’ (x) = u’ + v’ Contoh 1 : f(x) f’(x) = (3 x 3 + 10) + (5 x 2 + 6) = (9 x 2) + (10 x) Contoh 2 : f(x) f’(x) = (2 x 5 + 6 x) + (3 x 2 + 10 x) = (10 x 4 + 6) + (6 x + 10) = 10 x 4 + 6 x + 16

4. f (x) = u. v f’ (x) = u’v + v’u Contoh 1 : f(x) = (2 x 5 + 3). (3 x 2 + 1) f’x) = (10 x 4) (3 x 2 + 1) + (6 x) (2 x 5 + 3) = (30 x 6 + 10 x 4) + (12 x 6 + 18 x) = 42 x 6 + 10 x 4 + 18 x

Pertemuan ke tujuh latihan soal -soal diff fungsi aljabar

LATIHAN SOAL 1. f(x) = (x 3+3) – (x 4+4 x 2) 2. f(x) = (x 3+3 x 2) + (x 3+5 x) 3. f(x) = (x 3+4 x 2+5 x+10) 4. f(x) = (x 5+3 x). (x 2+2 x) 5. f(x) = (x 3 + 2 x) 1/2
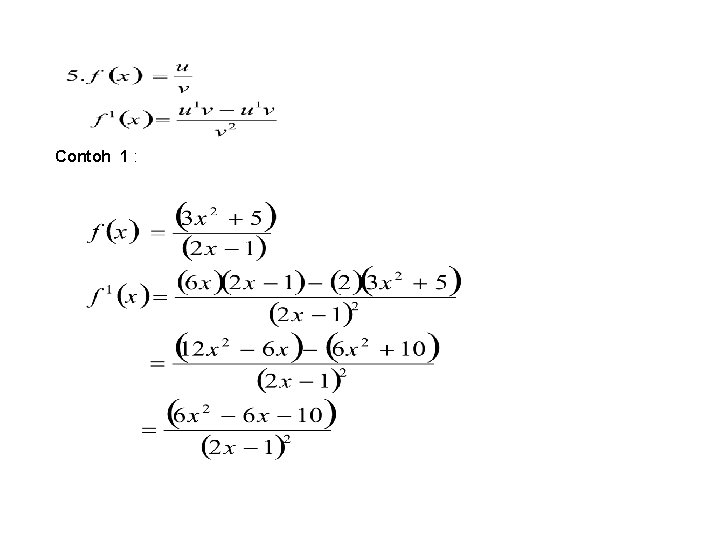
Contoh 1 :
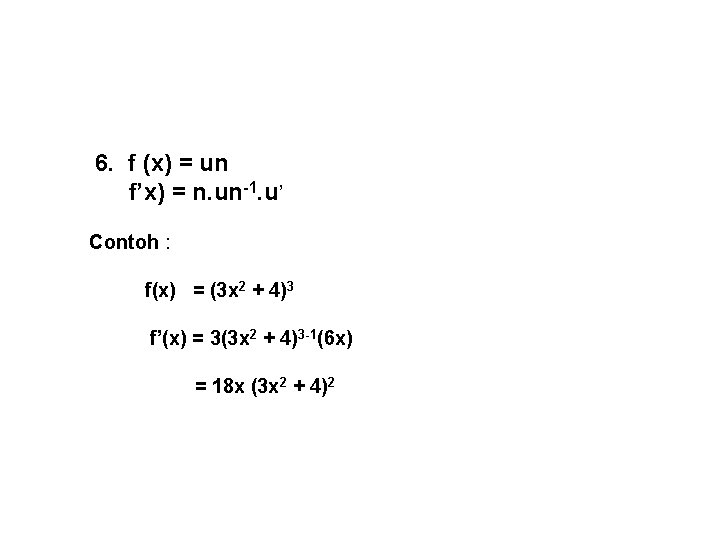
6. f (x) = un f’x) = n. un-1. u’ Contoh : f(x) = (3 x 2 + 4)3 f’(x) = 3(3 x 2 + 4)3 -1(6 x) = 18 x (3 x 2 + 4)2
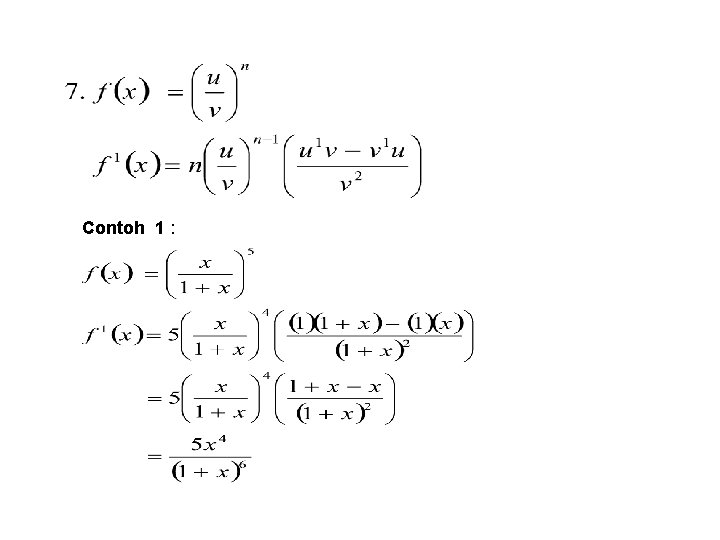
Contoh 1 :

Pertemuan ke lapan Quisioner

QUISIONER f(x) = (x 3 + 5) (2 x + 1) f(x) = (x 2 – 1) + (3 x 2 +3 x+7) f(x) = (4 x 5 + 10) – (3 x 3 + 2 x) f(x) = (2 x 3+3 x)5

Pertemuan ke sembilan diff fungsi implisit

Fungsi Implisit Differensial secara implisit, caranya differensialkan variabel x seperti biasa, kemudian differensialkan variabel y seperti variabel x, tetapi harus dikalikan dengan dy/dx

Pertemuan ke sepuluh latihan soal-soal diff fungsi implisit

Latihan soal-soal untuk fungsi implisit selesaikanlah differensial fungsi implisit berikut ini :

Pertemuan ke sebelas diff fungsi trigonometri

Fungsi Trigonometri Tabel 1. Koefisien Differensial Baku No y = f(x) 1 sin x cos x 2 cos x -sin x 3 tg x sec 2 x 4 ctg x -cosec 2 x 5 sec x tg x 6 Cosec x -cosec x tg x

Pertemuan ke duabelas diff fungsi eksponen

FUNGSI EKSPONEN DAN LOGARIMA

Pertemuan ke tigabelas latihan soal-soal diff fungsi exponen dan logaritma

CONTOH PENYELESAIAN SOAL-SOAL. y = ex 1 2. y = 2 e 3 x 3. y = ln x 4. y = ax 5. log a x 6. y = e(3 -x)

Pertemuan ke empatbelas mid test

MID TEST SELESAIKANLAH DIFFERENSIAL FUNGSI-FUNGSI BERIKUT INI DENGAN WAKTU 60 MENIT. 1. f(x) = ( 2 x 4 + 3 x 2 + 5 x + 55 ) 2. f(x) = ( 3 x 2 + 5 x 3 ) + ( 4 x 3 - 2 x 3 ) 3. f(x) = ( 3 x 4 + 5 x 2 ) 7 4. f(x) = ( 3 x 3_ 4 x 2 ). ( 2 x 4 + 5 x ) 5. f(x) = sin 2 x 3 + 3 tg 2 x 6. f(x) = ( cos 3 x + 5 ). ( sin 3 x 2 ) 7. f(x) = ( e 3 x + 5 x 2 ) + ( sin 3 x 2 + 5 )

Pertemuan ke limabelas penerapan differensial

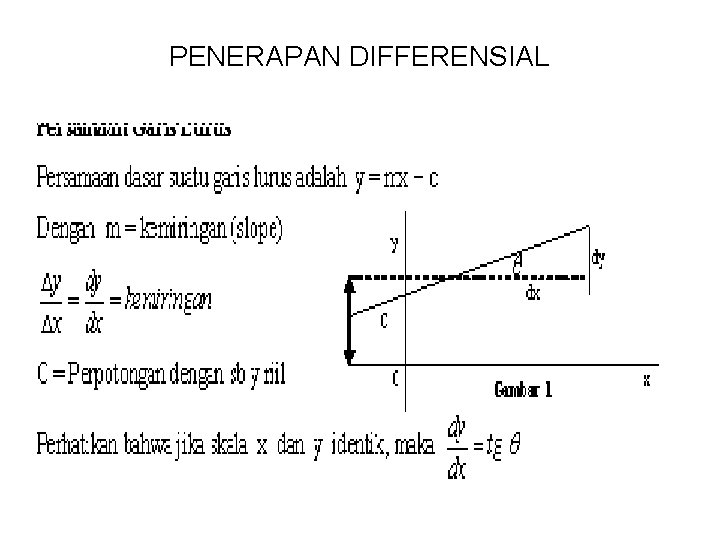
PENERAPAN DIFFERENSIAL

• Garis Singgung dan Garis Normal suatu kurva disebuah titik tertentu. Kemiringan kurva y = f(x) disebuah titik P pada kurva ditentukan oleh kemiringan garis singgungnya dititik P. Kemiringan ini juga diberikan oleh harga dititik P. Yang dapat dihitung bila persamaan kurvanya diketahui. Jadi kita dapat menghitung kemiringan garis singgung suatu kurva dititik P. Kita tahu bahwa garis singgung tersebut melalui titik P, yaitu bila x = x 1 dan y = y 1. • Persamaan garis untuk menghitung kemiringan adalah: y-y 1 = m (x-x 1)

JARI-JARI KELENGKUNGAN

Pertemuan ke enambelas latihan soal penerapan differensial

Latihan soal 1. Tentukanlah jari-jari kelengkungan kurva dititik (2, 3) 2. Tentukanlah persamaan garis singgung dari garis normal kurva y = x 3 – 2 x 2 + 3 x – 1 dititik (2, 5).

Pertemuan ke tujubelas Integral

INTEGRAL Pengertian Integral boleh disebut sebagai “anti turunan” atau kebalikan dari differensial, kalau dalam differensial pangkat dari variabel x berkurang satu, sebaliknya dalam integral pangkat dari variabel x bertambah satu. Dalam operasi matematika ada dua macam operasi yang saling berlawanan, operasi yang demikian merupakan operasi balikan (inversi). Dalam operasi balikan itu misalnya pengurangan dan penambahan, perkalian dan pembagian, pemangkatan dan penarikan akar serta penarikan logaritma dan perhitungan logaritma.

MACAM –MACAM INTEGRAL Dalam menyelesaikan suatu fungsi integral, maka perlu kita ketahui bahwa ada beberapa macam fungsi yang dapat dikelompokkan sebagai beriktu : • Integral tak tentu • Integral parsiil • Integral fungsi rasional • Integral fungsi trigonometri • Integral logaritma dan exponen • Integral denan substitusi

RUMUS-RUMUS DASAR
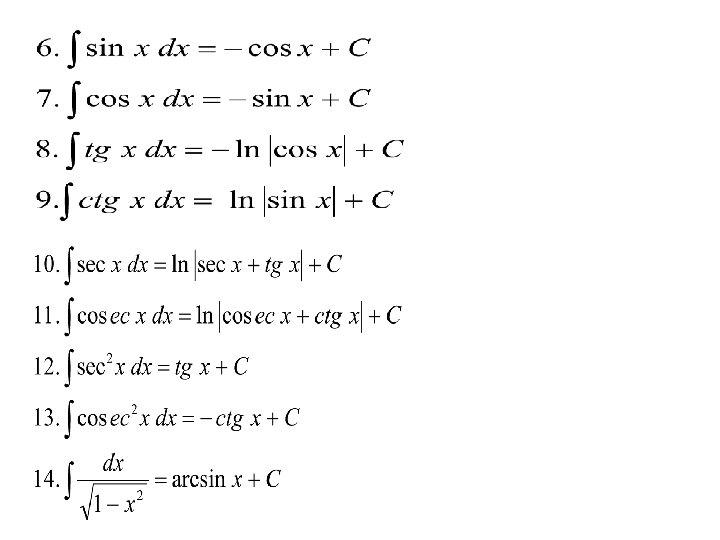

Pertemuan ke delapanbelas Integral tak tentu

INTEGRAL TAK TENTU

INTEGRAL TAK TENTU Contoh-contoh

Pertemuan ke sembilanbelas Integral dengan substitusi

INTEGRAL DENGAN SUBSTITUSI Misalnya : x 3 + 2 = u 3 x 2 dx = du
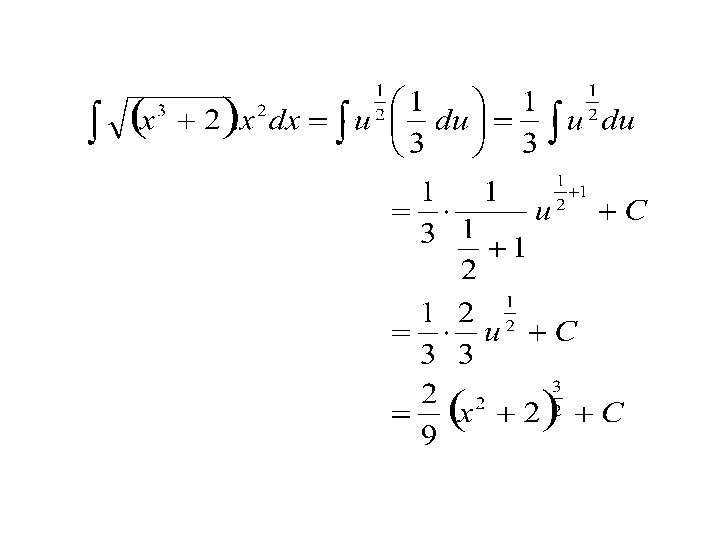

Pertemuan ke duapuluh latihan soal-soal integral tak tentu dan integral dg substitusi

Latihan soal

Pertemuan ke duapuluhsatu Integral parsiil

INTEGRAL PARSIIL Suatu bentuk integral yang sering timbul, ialah suatu integral yang integralnya merupakan hasil ganda dari suatu fungsi x dengan differensial dari fungsi x yang lain. Andaikan u dan v adalah fungsi dari x, maka dicari hasil dari bentuk : Agar kita dapat menggunakan rumus ini, bentuk dari integral yang kita ketahui harus dibuat menjadi dua bagaian satu bagain sesuai dengan u dan bagian yang lain bersama-sama dengan dx sesuai dv. Untuk lebih jelasnya kita ambil beberapa

Contoh Integral parsiil

Pertemuan ke duapuluhdua latihan soal-soal Integral parsiil

Latihan soal

Pertemuan ke duapuluhtiga Integral fungsi rasional

Integral fungsi rasional Dalam menyelesaikan integral fungsi rasional ada cara yang dapat digunakan agar penyelesaian tersebut dapat dengan mudah kita selesaikan. Caranya adalah sebagai berikut : Bagian kiri identik dengan bagian kanan, berarti koefisien dari x yang berpangkat sama dari kedua bagian tersebut harus sama.

CONTOH INTEGRAL FUNGSI RASIONAL dalam hal ini x 3 – 7 x + 6 kita uraikan dalam bentuk faktor :

Maka persamaan menjadi :

Pertemuan ke duapululima latihan soal-soal Integral fungsi rasional

LATIHAN SOAL FUNGSI RASIONAL

Pertemuan ke duapuluenam latihan soal-soal campuran

Slatihan soal-soal campuran 1. f(x) = (x 3 + 5) (2 x + 1) 2. f(x) = (x 2 – 1) + (3 x 2 +3 x+7) 3. f(x) = (4 x 5 + 10) – (3 x 3 + 2 x) 4. f(x) = (2 x 3+3 x)5

Pertemuan ke duapulutujuh latihan soal-soal campuran

Slatihan soal-soal campuran 1. f(x) = (x 3 + 5) (2 x + 1) 2. f(x) = (x 2 – 1) + (3 x 2 +3 x+7) 3. f(x) = (4 x 5 + 10) – (3 x 3 + 2 x) 4. f(x) = (2 x 3+3 x)5

Pertemuan ke duapuluhdelapan ujian semester
 Mahasiswa takut pada dosen
Mahasiswa takut pada dosen Silabus mata kuliah seminar proposal skripsi
Silabus mata kuliah seminar proposal skripsi Matkul ekonomi pembangunan ub
Matkul ekonomi pembangunan ub Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Mata kuliah manajemen investasi
Mata kuliah manajemen investasi Mata kuliah mikrokontroler
Mata kuliah mikrokontroler Mata kuliah struktur beton
Mata kuliah struktur beton Mata kuliah geografi
Mata kuliah geografi Mata kuliah institusional adalah
Mata kuliah institusional adalah Rekonstruksi mata kuliah
Rekonstruksi mata kuliah Gambar
Gambar Mata kuliah metode penelitian teknik informatika
Mata kuliah metode penelitian teknik informatika Materi pengantar ilmu pendidikan semester 1
Materi pengantar ilmu pendidikan semester 1 Mata kuliah etika profesi
Mata kuliah etika profesi Mata kuliah teknologi bahan
Mata kuliah teknologi bahan Relevansi mata kuliah menyimak dengan berbicara
Relevansi mata kuliah menyimak dengan berbicara Mata kuliah geografi ui
Mata kuliah geografi ui Mata kuliah sistem produksi
Mata kuliah sistem produksi Hampiran adalah
Hampiran adalah Materi tentang keamanan jaringan
Materi tentang keamanan jaringan Mata kuliah probabilitas dan statistika
Mata kuliah probabilitas dan statistika Mata kuliah komputer dan masyarakat
Mata kuliah komputer dan masyarakat Cpmk
Cpmk Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Mata kuliah pelayanan prima
Mata kuliah pelayanan prima Lacrisert adalah
Lacrisert adalah Mata kuliah teknik digital
Mata kuliah teknik digital Mata kuliah promosi kesehatan
Mata kuliah promosi kesehatan Teori dan perilaku organisasi anggri puspita sari
Teori dan perilaku organisasi anggri puspita sari Tugas mata kuliah metodologi penelitian
Tugas mata kuliah metodologi penelitian Mata kuliah ilmu alamiah dasar
Mata kuliah ilmu alamiah dasar Surat pengunduran diri gunadarma
Surat pengunduran diri gunadarma Mata kuliah ekonomi islam ub
Mata kuliah ekonomi islam ub Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Mata kuliah ilmu kelautan unpad
Mata kuliah ilmu kelautan unpad Mata kuliah farmasi ugm
Mata kuliah farmasi ugm Materi pengembangan diri mahasiswa
Materi pengembangan diri mahasiswa Erd adalah
Erd adalah Materi kuliah manajemen keuangan
Materi kuliah manajemen keuangan Deskripsi mata kuliah pengantar bisnis
Deskripsi mata kuliah pengantar bisnis Mata kuliah seminar akuntansi
Mata kuliah seminar akuntansi Administrasi publik upi
Administrasi publik upi Silabus sejarah pendidikan islam
Silabus sejarah pendidikan islam Proses mapping risiko
Proses mapping risiko Cjr mata kuliah kewirausahaan
Cjr mata kuliah kewirausahaan Mata kuliah sik
Mata kuliah sik Klasifikasi sistem manufaktur
Klasifikasi sistem manufaktur Contoh soal modal kerja mata kuliah manajemen keuangan
Contoh soal modal kerja mata kuliah manajemen keuangan Mata kuliah manajemen proyek sistem informasi
Mata kuliah manajemen proyek sistem informasi Deklarasi jakarta 1997
Deklarasi jakarta 1997 Rangkuman mata kuliah sistem informasi manajemen
Rangkuman mata kuliah sistem informasi manajemen Sap universitas gunadarma
Sap universitas gunadarma Mata kuliah fisika lingkungan
Mata kuliah fisika lingkungan Rekonstruksi mata kuliah
Rekonstruksi mata kuliah Mata kuliah pemrograman visual
Mata kuliah pemrograman visual Contoh analisis kebijakan pendidikan
Contoh analisis kebijakan pendidikan Deskripsi mata kuliah ekonomi mikro
Deskripsi mata kuliah ekonomi mikro Mata kuliah manajemen investasi dan pasar modal
Mata kuliah manajemen investasi dan pasar modal Erd kuliah
Erd kuliah Mata kuliah mercu buana
Mata kuliah mercu buana Csm erp
Csm erp Mata kuliah struktur beton
Mata kuliah struktur beton Risk financing
Risk financing Mata kuliah penyuntingan
Mata kuliah penyuntingan Soal uas mata kuliah perencanaan pembelajaran
Soal uas mata kuliah perencanaan pembelajaran Mata kuliah keamanan sistem informasi
Mata kuliah keamanan sistem informasi Mata kuliah geografi ui
Mata kuliah geografi ui Mata kuliah testing dan implementasi sistem
Mata kuliah testing dan implementasi sistem Mata kuliah administrasi perpajakan ui
Mata kuliah administrasi perpajakan ui Kurikulum sistem informasi gunadarma
Kurikulum sistem informasi gunadarma Pertanyaan tentang tugas-tugas perkembangan peserta didik
Pertanyaan tentang tugas-tugas perkembangan peserta didik Mata kuliah advokasi
Mata kuliah advokasi Deskripsi mata kuliah pengantar bisnis
Deskripsi mata kuliah pengantar bisnis Mata kuliah keamanan sistem informasi
Mata kuliah keamanan sistem informasi Mata kuliah aplikasi komputer statistik
Mata kuliah aplikasi komputer statistik Mata kuliah analisis jabatan
Mata kuliah analisis jabatan Mata kuliah teknik industri
Mata kuliah teknik industri Mata kuliah profesi keguruan
Mata kuliah profesi keguruan