MATA KULIAH KALKULUS III 4 sks DOSEN Ir






















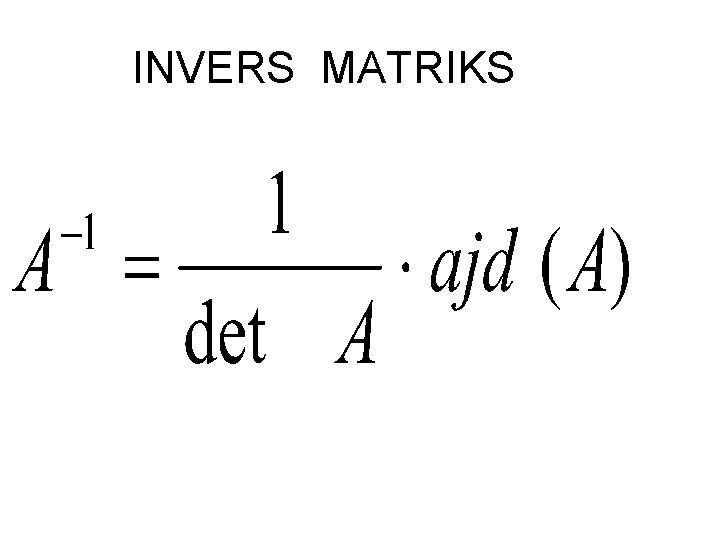












































- Slides: 72

MATA KULIAH KALKULUS III (4 sks) DOSEN : Ir. RENILAILI, MT

MINGGU PERTAMA

MATRIKS PENGERTIAN MATRIKS Matriks adalah sekumpulan bilangan riil atau kompleks yang disususn menurut baris dan kolom sehingga membentuk jajaran persegi panjang. Matriks yang mempunyai m baris dan n kolom disebut m x n atau matriks berordo m x n.

MACAM-MACAM MATRIKS 1. Matriks Nol adalah suatu matriks yang semua elemen-elemennya adalah nol. Contoh : 2 Matriks Bujur Sangkar adalah matriks m x n atau banyak baris = banyaknya kolom Contoh :

3. Matriks Diagonal adalah matriks bujur sangkar yang semua elemennya sama dengan nol, kecuali elemen pada diagonal utamanya. Contoh :

4. Matriks satuan/Matriks Indentitas adalah matriks diagonal yang semua elemen diagonal utmanya = 1 Contoh :

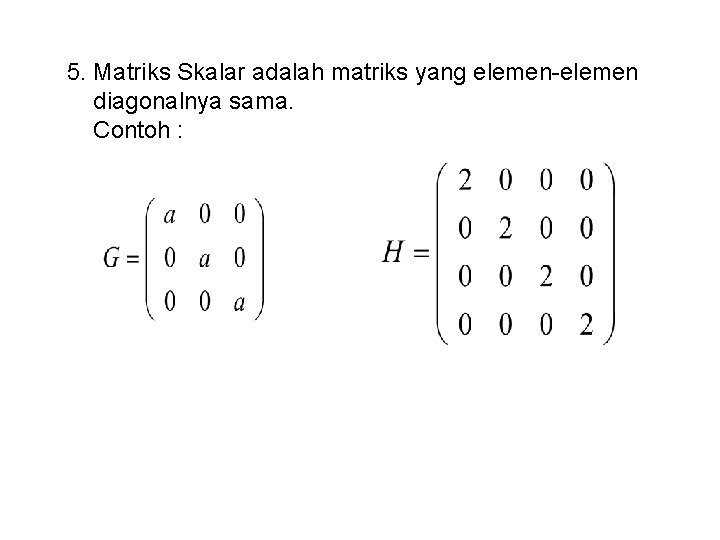
5. Matriks Skalar adalah matriks yang elemen-elemen diagonalnya sama. Contoh :

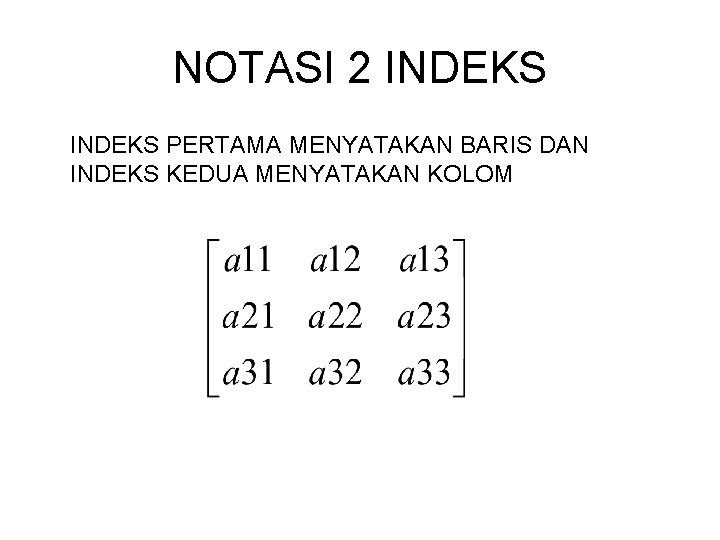
NOTASI 2 INDEKS PERTAMA MENYATAKAN BARIS DAN INDEKS KEDUA MENYATAKAN KOLOM

OPERASI DASAR MATRIKS • • • PENJUMLAHAN MATRIKS PENGURANGAN MATRIKS PERKALIAN MATRIKS TRANSFOSE MATRIKS DETERMINAN MATRIKS INVERS MATRIKS

PENJUMLAHAN MATRIKS

PENGURANGAN MATRIKS

PERKALIAN MATRIKS K x =

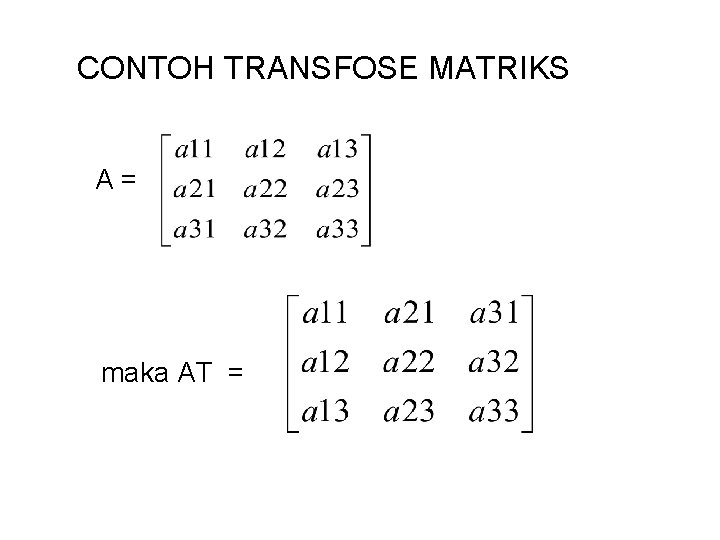
TRANSFOSE MATRIKS Jika baris dan kolom suatu matriks dipertukarkan maksudnya baris menjadi kolom dan kolom menjadi baris, maka matriks baru yang terbentuk disebut transpose dari matriks semula.

CONTOH TRANSFOSE MATRIKS A= maka AT =

DETERMINAN MATRIKS Ada 3 metode yang bisa dipakai untuk menghitung determinan 3 x 3 yaitu: Metode Sarruss Metode kofaktor (atas) Metode kofaktor (bawah) Untuk determinan 2 x 2 cukup berlaku ad-bc

Determinan 2 x 2 Contoh: Det A = 2. 5 – 4. 7=10 -28 = - 18

DETERMINAN 3 X 3 METODE SARRUSS METODE KOFAKTOR (ATAS) KOFAKTOR (SAMPING)

METODE SARRUSS

METODE KOFAKTOR

CONTOH

LATIHAN SOAL-SOAL 1. 2. 3. 4. Buatlah contoh dari macam-macam matrik. Buatlah masing-masing contoh matriks 2 x 2 dan 3 x 3 Dari matriks yang anda buat untuk matriks yang 2 x 2 hitunglah masing-masing penjumlahan, pengurangandan perkaliannya. Untuk matriks yang 3 x 3 hitunglah determinan dengan 3 cara yang sudah dipelajari sebelumnya. Usahakan kerjakan soal-soal tepat dalam waktu 1 jam.

INVERS MATRIKS UNTUK MATRIKS YANG 2 X 2

INVERS MATRIKS 3 X 3

MATRIKS KOFAKTOR

ADJOINT MATRIKS
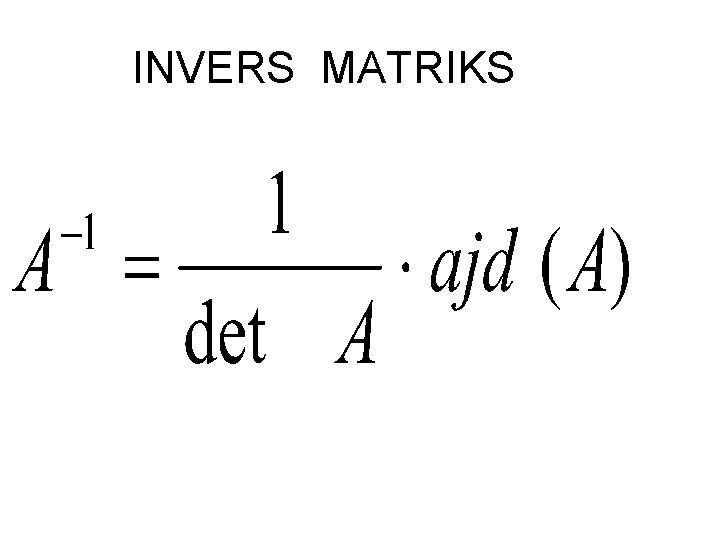
INVERS MATRIKS


PERSAMAAN DIFFERENSIAL Pengertian Persamaan Differensial adalah hubungan antara variabel bebas x, variabel tak bebas y, dan satu atau lebih koefisien differensial y terhadap x. Persamaan differensial menyatakan hubungan dinamik, maksudnya hubungan tersebut memuat besaran-besaran yang berubah dan karena itu persamaan differensial sering muncul dalam persoalan ilmu pengetahuan dan teknik. Orde suatu persamaan differensial ditentukan oleh turunan tertinggi yang terdapat dalam persamaan tersebut.

Contoh persamaan differensial untuk orde I , II dan III

Pembentukan Persamaan Differensial Dalam prakteknya, persamaan differensial dapat dibentuk dari pengkajian persoalan fisis yang dinyatakannya. Secara matematis persamaan differensial muncul bila ada konstanta sembarang dieleminasikan dari suatu fungsi tertentu yang diberikan. Contoh 1 : setelah dua kali differensial ternyata persamaan diatas tepat sama dengan persamaan semula hanya tandanya yang berlawanan. Jadi persamaan orde 2.

CONTOH 2. Diketahui : fungsi Ditanya : Bentuklah persamaan differensial dari fungsi diatas Penyelesaian : Substitusi persamaan ii dan iv

PEMECAHAN PERSAMAAN DIFFERENSIAL Untuk memecahkan differensial, kita harus mencari fungsi yang memenuhi persamaan itu artinya yang membuat persamaan itu benar. Hal ini berarti kita harus mengolah persamaan tersebut sedemikian rupa sehingga semua koefisien differensialnya hilang dan tinggallah hubungan antara y dan x. Ada 2 cara yang dapat dilakukan yaitu: 1. Dengan Integral langsung

2. Dengan pemisahan variabel Jika persamaan yang diberikan berbentuk , maka variabel y yang muncul diruas kanan mencegah kita memecahkannya dengan integrasi langsung. Karena itu kita harus mencari cara pemecahan yang lain misalkan kita tinjau persamaan dalam bentuk : dan dalam bentuk yaitu persamaan yang ruas kanannya dapat dinyatakan sebagai perkalian atau pembagian fungsi x dan fungsi y, f (y).

Contoh 1 pada contoh tersebut kita ubh dulu menjadi : kemudian integrasikan kedua ruasnya terhadap x :

Contoh 2

LATIHAN SOAL-SOAL


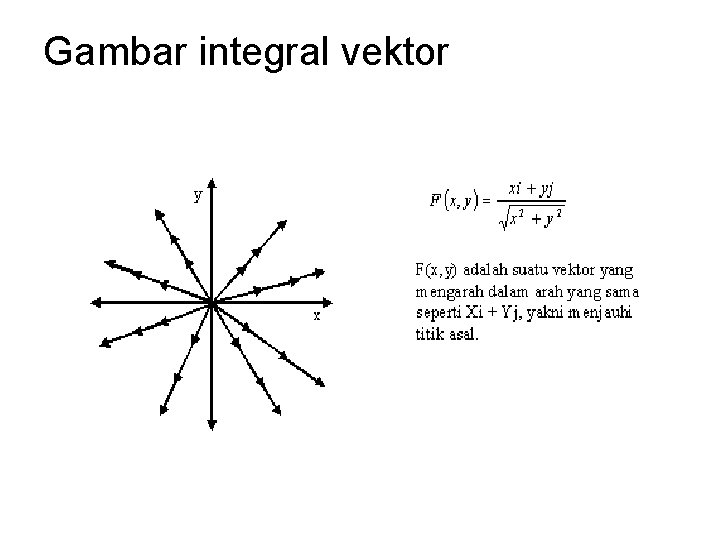
INTEGRAL VEKTOR Pengertian Integral Vektor Medan Vektor dapat diartikan hampir sama dengan medan-medan yang lain, yang muncul secara alamiah seperti medan listrik, medan magnit, medan gaya dan medan gravitasi. Kita hanya memandang kasus dimana medan-medan ini tidak tergantung pada waktu yang kita sebut dengan “MEDAN VEKTOR MANTAP”. Berlawanan dengan suatu medan vektor suatu fungsi F yang mengaitkan suatu bilangan dengan uap titik didalam ruang disebut medan skalar fungsi yang memberikan suhu pada tiap titik akan merupakan sebuah contoh fisis yang bagus dari suatu medan skalar.

Gambar integral vektor

Divergensi Dan Curl Dari Medan Vektor Misalkan F = Mi + Nj + Pk adalah medan vektor

Bilamana beroperasi pada suatu f, ia akan menghasilkan gradien yaitu :

CONTOH 1. Tentukan div F dan curl F dari fungsi : Penyelesaian :

CONTOH 2. Tentukan div F dan curl F dari fungsi :

MINGGU KEEMPAT

KUISIONER

MINGGU KELIMA

INTEGRAL GARIS Integral Garis , disebut juga dengan integral curva yang dapat ditulis sebagai integral ini dapat dirumuskan sebagai berikut :

CONTOH Hitunglah Integral Curva dari fungsi sebagai berikut : dengan C ditentukan oleh persamaan parameter x = 3 cos t dan y = 3 sin t, Penyelesaian X = 3 cost t dx = -3 sin t dt

Latihan soal-soal 1. Tentukanlah Div F dan curl F dari fungsi berikut : F(x, y, z) = (x 3 y 2 z)i + (2 x y 2 z 3)j + (3 x 2 + z 3)k 2. Tentukanlah div F dan curl F dari fungsi berikut : F(x, y, z) = (2 x 4 y z 3)i + (x 3 y 4 z)j + (x 3 + 2 x 4)k 3. Hitunglah integral curva dari fungsi sebagai berikut : dengan C ditentukan oleh persamaan parameter x = 5 sin t dan y = 5 cos t,

MID TEST

PERSAMAAN DIFFERENSIAL PARSIIL

CONTOH

CONTOH

LATIHAN SOAL-SOAL

MINGGU KESEBELAS

DERET MACLAURINE

CONTOH DERET MACLAURINE

LATIHAN SOAL 1. f(x) = ex turunkan sampai f. IV(x) 2. f(x) = Cos 2 x turunkan sampai f. IV(x)

MINGGU KEDUABELAS

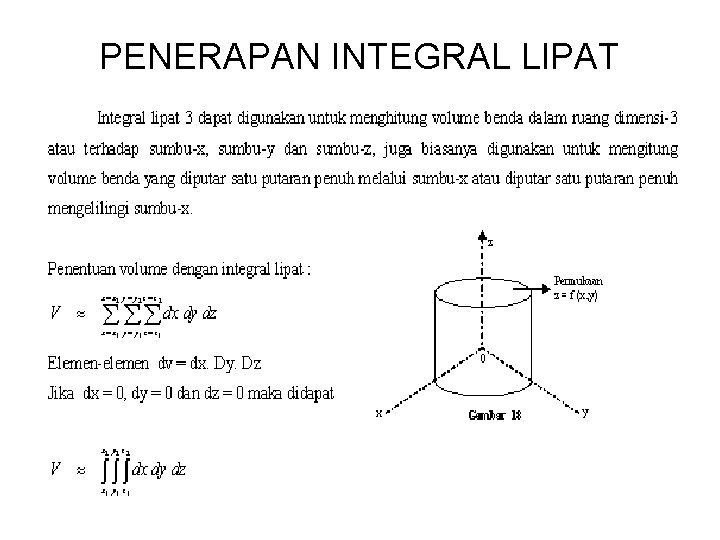
PENERAPAN INTEGRAL LIPAT

CONTOH SOAL


MINGGU KETIGABELAS

VOLUME BENDA PUTAR


CONTOH SOAL

MINGGU KEEMPATBELAS

PUSAT GRAVITASI SUATU BENDA PUTAR

MINGGU KELIMABELAS

LATIHAN SOAL

MINGGU KEENAMBELAS UJIAN AKHIR SEMESTER

DAFTAR PUSTAKA
 Mahasiswa takut pada dosen
Mahasiswa takut pada dosen Mata kuliah sik
Mata kuliah sik Perencanaan dan pengendalian produksi
Perencanaan dan pengendalian produksi Mata kuliah manajemen proyek sistem informasi
Mata kuliah manajemen proyek sistem informasi Deklarasi jakarta 1997
Deklarasi jakarta 1997 Rangkuman mata kuliah sistem informasi manajemen
Rangkuman mata kuliah sistem informasi manajemen Sap universitas gunadarma
Sap universitas gunadarma Materi kuliah fisika lingkungan
Materi kuliah fisika lingkungan Silabus metode penelitian
Silabus metode penelitian Rekonstruksi mata kuliah
Rekonstruksi mata kuliah Tujuan pemrograman visual
Tujuan pemrograman visual Contoh analisis kebijakan pendidikan
Contoh analisis kebijakan pendidikan Mata kuliah etika profesi
Mata kuliah etika profesi Mata kuliah manajemen investasi dan pasar modal
Mata kuliah manajemen investasi dan pasar modal Mata kuliah mercu buana
Mata kuliah mercu buana Mata kuliah erp
Mata kuliah erp Contoh cpmk mata kuliah
Contoh cpmk mata kuliah Beton
Beton Contoh risk financing transfer
Contoh risk financing transfer Mata kuliah penyuntingan
Mata kuliah penyuntingan Mata kuliah pelayanan prima
Mata kuliah pelayanan prima Soal uas mata kuliah perencanaan pembelajaran
Soal uas mata kuliah perencanaan pembelajaran Mata kuliah keamanan sistem informasi
Mata kuliah keamanan sistem informasi Mata kuliah geografi ui
Mata kuliah geografi ui Mata kuliah administrasi perpajakan ui
Mata kuliah administrasi perpajakan ui Pertanyaan tentang psikologi perkembangan peserta didik
Pertanyaan tentang psikologi perkembangan peserta didik Mata kuliah advokasi
Mata kuliah advokasi Mata kuliah ilmu kelautan unpad
Mata kuliah ilmu kelautan unpad Silabus mata kuliah pengantar bisnis
Silabus mata kuliah pengantar bisnis Mata kuliah keamanan sistem informasi
Mata kuliah keamanan sistem informasi Pengantar aplikasi komputer (spss)
Pengantar aplikasi komputer (spss) Mata kuliah analisis jabatan
Mata kuliah analisis jabatan Materi kuliah pengembangan diri
Materi kuliah pengembangan diri Mata kuliah teknik industri
Mata kuliah teknik industri Mata kuliah profesi keguruan
Mata kuliah profesi keguruan Mata kuliah pendidikan inklusi
Mata kuliah pendidikan inklusi Silabus mata kuliah seminar proposal skripsi
Silabus mata kuliah seminar proposal skripsi Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Mata kuliah manajemen investasi
Mata kuliah manajemen investasi Mata kuliah mikrokontroler
Mata kuliah mikrokontroler Cjr mata kuliah kewirausahaan
Cjr mata kuliah kewirausahaan Mata kuliah struktur beton
Mata kuliah struktur beton Materi kuliah geografi ekonomi
Materi kuliah geografi ekonomi Kurikulum institusional adalah
Kurikulum institusional adalah Contoh soal modal kerja mata kuliah manajemen keuangan
Contoh soal modal kerja mata kuliah manajemen keuangan Rekonstruksi mata kuliah adalah
Rekonstruksi mata kuliah adalah Kode pensil yang paling cocok untuk teknik dusel adalah
Kode pensil yang paling cocok untuk teknik dusel adalah Kontrak perkuliahan
Kontrak perkuliahan Mata kuliah teknologi bahan
Mata kuliah teknologi bahan Deskripsi mata kuliah ekonomi mikro
Deskripsi mata kuliah ekonomi mikro Relevansi mata kuliah menyimak dengan berbicara
Relevansi mata kuliah menyimak dengan berbicara Mata kuliah geografi ui
Mata kuliah geografi ui Mata kuliah sistem produksi
Mata kuliah sistem produksi Erd mata kuliah
Erd mata kuliah Hampiran adalah
Hampiran adalah Jenis ancaman keamanan komputer
Jenis ancaman keamanan komputer Mata kuliah statistika dan probabilitas
Mata kuliah statistika dan probabilitas Mata kuliah komputer dan masyarakat
Mata kuliah komputer dan masyarakat Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Lacrisert adalah
Lacrisert adalah Mata kuliah teknik digital
Mata kuliah teknik digital Deklarasi alma ata
Deklarasi alma ata Mata kuliah testing dan implementasi sistem
Mata kuliah testing dan implementasi sistem Uts perilaku organisasi
Uts perilaku organisasi Tugas mata kuliah metodologi penelitian
Tugas mata kuliah metodologi penelitian Mata kuliah ilmu alamiah dasar
Mata kuliah ilmu alamiah dasar Sks sistem informasi gunadarma
Sks sistem informasi gunadarma Contoh pi psikologi gunadarma
Contoh pi psikologi gunadarma Matkul ekonomi islam ub
Matkul ekonomi islam ub Mata kuliah pengantar arsitektur
Mata kuliah pengantar arsitektur Abdul rohman ugm
Abdul rohman ugm Penjelasan erd
Penjelasan erd Mata kuliah creative writing
Mata kuliah creative writing