MAT 101 Temel Matematik Mustafa Sezer PEHLVAN Yksek

MAT – 101 Temel Matematik * Mustafa Sezer PEHLİVAN Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü

KARTEZYEN ÇARPIMI İlk elemanı birinci kümeden, ikinci elemanı ikinci kümeden gelen ikililerin oluşturduğu kümeye Kartezyen Çarpımı denir. Örnek : A = {a, b} ve B = {1, 2, 3} ise A x B = {(a, 1), (b, 1), (a, 2), (b, 2), (a, 3), (b, 3)} olur. B x A = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)} şeklinde yazılır. Mustafa Sezer PEHLİVAN

KARTEZYEN ÇARPIMI Örnekte olduğu gibi; A x B ≠ B x A (Kartezyen çarpım işleminin değişme özelliği yoktur. ) Yine örnekte görüldüğü gibi A kümesinin 3, B kümesinin 2 elemanı vardır. Ax. B kümesinin eleman sayısı ise 6 ‘dır. Mustafa Sezer PEHLİVAN

KARTEZYEN ÇARPIMI Çünkü kartezyen çarpım kümesinin eleman sayısı ; kartezyen çarpımı oluşturan kümelerin eleman sayılarının çarpımına eşittir. s(Ax. B) = s(Bx. A) = s(A). s(B) Mustafa Sezer PEHLİVAN

BAĞINTI Kartezyen çarpım kümesinin herhangi bir alt kümesine Bağıntı denir. Eğer bağıntı, Ax. B ‘nin alt kümesi ise o bağıntıya A’dan B’ye bir bağıntı denir. Buradaki birinci küme, bağıntının tanım kümesi ; ikinci küme ise bağıntının değer kümesi olarak adlandırılır. Mustafa Sezer PEHLİVAN

BAĞINTI “n” elemanlı bir kümenin tüm bağıntılarının sayısı 2 n olduğundan dolayı A’dan B’ye yazılabilecek tüm bağıntıların sayısı da 2 s(A). s(B)’ dir. Örneğin; s(A) = 4 ve s(B) = 3 ise A’dan B’ye yazılabilecek tüm bağıntıların sayısı 212 olur. Tabii ki aynı şekilde B’den A’ya yazılabilecek tüm bağıntıların sayısı da 212 ‘dir. Mustafa Sezer PEHLİVAN

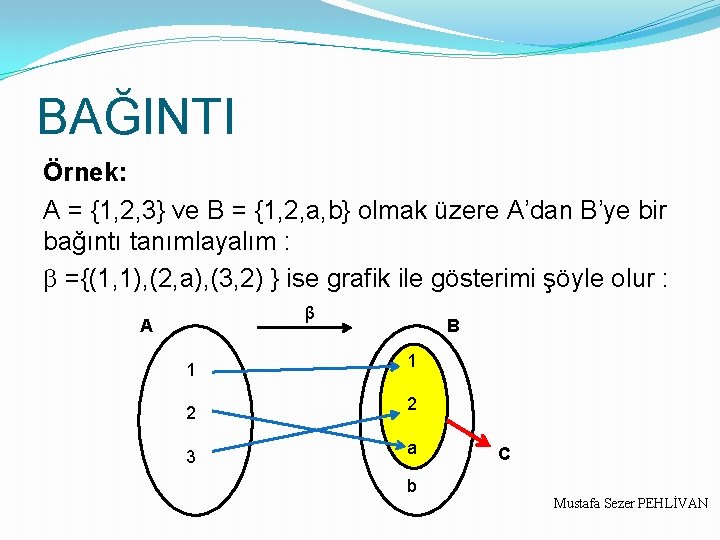
BAĞINTI Örnek: A = {1, 2, 3} ve B = {1, 2, a, b} olmak üzere A’dan B’ye bir bağıntı tanımlayalım : b ={(1, 1), (2, a), (3, 2) } ise grafik ile gösterimi şöyle olur : β A 1 2 3 B 1 2 a b C Mustafa Sezer PEHLİVAN

BAĞINTI b : A B olmak üzere tanımlanmış; A tanım kümesi, B değer kümesi, C ise görüntü kümesi olarak tanımlanır. Örnek üzerinden tanımlarsak; C = b (A) = {b(1), b(2), b(3)} = {1, 2, a} kümesine görüntü kümesi denir ve görüntü kümesi her zaman değer kümesi ile aynı anlama gelmeyebilir. Mustafa Sezer PEHLİVAN

FONKSİYON A ve B boş olmayan iki küme olsun. A’nın her elemanını B’nin bir tek elemanı ile eşleyen f bağıntısına A dan B ye bir fonksiyon denir ve f f: A B, A B veya x f(x)=y biçiminde gösterilir. A kümesine fonksiyonun tanım kümesi, B kümesine ise değer kümesi denir. Mustafa Sezer PEHLİVAN

FONKSİYON Şekilde A dan B ye tanımlanan f fonksiyonu f = {(a, 1), (b, 2), (c, 3), (d, 2)} biçiminde de gösterilir. Mustafa Sezer PEHLİVAN

FONKSİYON Eğer bağıntı; tanım kümesinin her elemanını değer kümesinin yalnız ve yalnız bir tek elemanına eşliyorsa o bağıntıya fonksiyon denir. Yani her bağıntı bir fonksiyon değil ama her fonksiyon aynı zamanda bir bağıntıdır. Mustafa Sezer PEHLİVAN

FONKSİYON Not: Verilen bir bağıntının fonksiyon olabilmesi için; �Tanım kümesinde açıkta eleman kalmamalıdır. Değer kümesinde açıkta eleman kalabilir. Yani tanım kümesinin her elemanının kullanılmış olması gerekir. �Tanım kümesinin her elemanının yalnız bir tane eşi- değeri- olmalıdır. Mustafa Sezer PEHLİVAN

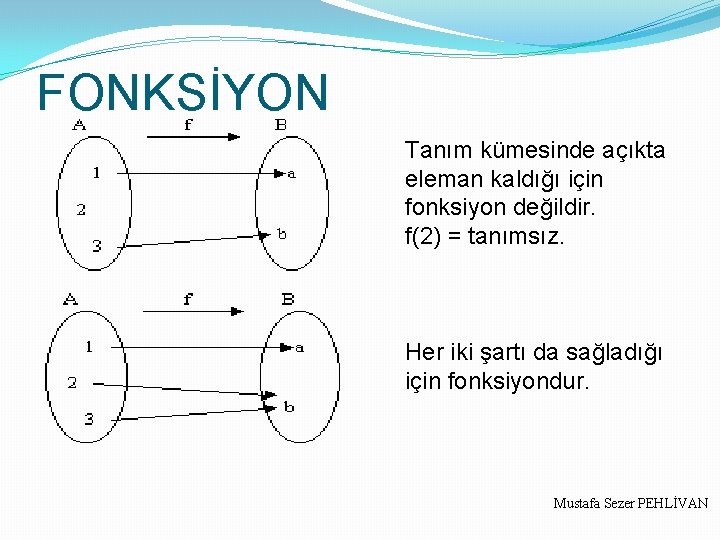
FONKSİYON f(2)=1 ve f(2)=2 olduğundan yani 2 elemanının 1’den fazla değeri olduğu için fonksiyon değildir. Mustafa Sezer PEHLİVAN

FONKSİYON Tanım kümesinde açıkta eleman kaldığı için fonksiyon değildir. f(2) = tanımsız. Her iki şartı da sağladığı için fonksiyondur. Mustafa Sezer PEHLİVAN

FONKSİYON Tanım kümesinin bir x elemanı, değer kümesinin bir y elemanına f ile bağlı ise bunu, bağıntıda kullanılan (x, y) ϵ f şeklinde gösterim yerine f: x y veya genellikle y=f(x) biçiminde gösterilir. Mustafa Sezer PEHLİVAN

FONKSİYON Ø Her fonksiyon bir bağıntıdır. Fakat her bağıntı fonksiyon olmayabilir. Ø Görüntü kümesi değer kümesinin alt kümesidir. Ø s(A) = m ve s(B) = n olmak üzere, Ø A dan B ye nm tane fonksiyon tanımlanabilir. Ø B den A ya mn tane fonksiyon tanımlanabilir. Ø A dan B ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı 2 m. n – nm dir. Mustafa Sezer PEHLİVAN

FONKSİYON Ø Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği grafiği yalnız ve yalnız bir noktada kesiyorsa verilen bağıntı x ten y ye bir fonksiyondur. Mustafa Sezer PEHLİVAN

FONKSİYON Örnek: Aşağıda grafiği verilen gerçek sayılarda tanımlanmış fonksiyonun tanım, görüntü ve değer kümelerini bulunuz. Mustafa Sezer PEHLİVAN

FONKSİYON Çözüm: Tanım kümesi = [-1, 7] Değer kümesi = [-5, 8] Görüntü kümesi, değer kümesine eşit veya onun alt kümesi olabilir. Mustafa Sezer PEHLİVAN

FONKSİYON Örnek: Aşağıda gerçel sayılarda tanımlanmış olan bağıntı fonksiyon mudur ? -4 y x Mustafa Sezer PEHLİVAN

FONKSİYON Çözüm: Bu bağıntı, tanım kümesinin (-¥, -4) aralığındaki değerlerinin görüntüsü olmadığı için fonksiyon değildir. Aynı zamanda [-4, ¥) aralığındaki değerlerinin de birden fazla görüntüsü olduğu için fonksiyon değildir. Bu sebeplerin bir tanesi bile fonksiyon olmaması için yeterlidir. Mustafa Sezer PEHLİVAN

FONKSİYON TÜRLERİ İçine Fonksiyon Eğer fonksiyonun görüntü kümesi, değer kümesinin alt kümesi (değer kümesinin bazı elemanlarının tanım kümesinde karşılığı yok) ise bu tür fonksiyonlara İçine fonksiyon denir. İçine fonksiyonlarda değer kümesinde en az bir eleman açıktadır. Mustafa Sezer PEHLİVAN

Birebir Fonksiyon x 1, x 2 A için, f (x 1) = f (x 2) iken x 1 = x 2 ise, f fonksiyonu bire bir fonksiyondur Ya da f (x 1) f (x 2) iken x 1 x 2 ise, f fonksiyonu bire birdir. f, A dan B ye bir fonksiyon olsun. f nin tanım kümesindeki her farklı elemanının görüntüsü farklı ise, f fonksiyonuna bire bir (1 -1) fonksiyon denir. Mustafa Sezer PEHLİVAN

Birebir Fonksiyon A dan B ye tanımlanabilecek bire bir fonksiyonların sayısı, Mustafa Sezer PEHLİVAN

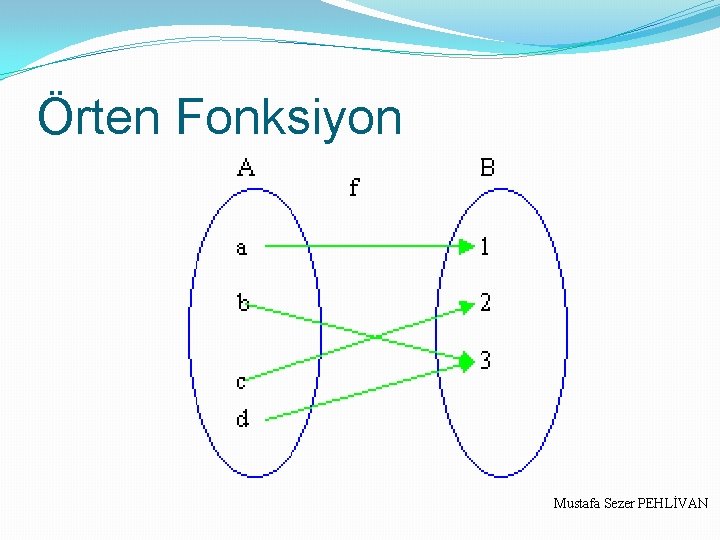
Örten Fonksiyon Görüntü kümesi, değer kümesine eşit olan fonksiyonlara örten fonksiyon denir. f : A → B f(A) = B ise, f örtendir. s(A) = m olmak üzere, A dan A ya tanımlanabilen bire bir örten fonksiyonların sayısı, m! = m × (m – 1) × (m – 2) ×. . . × 3 × 2 × 1 dir. Mustafa Sezer PEHLİVAN

Örten Fonksiyon Mustafa Sezer PEHLİVAN

Birim Fonksiyon Tanım kümesindeki her elemanın görüntüsü yine aynı ise bu tip fonksiyona birim fonksiyon denir ve ile gösterilir. f A f : A B f(a) = a, f(b) = b, f(c) = c dir. Buna göre, f birim fonksiyondur. B a. . a b. . b c. . c Mustafa Sezer PEHLİVAN

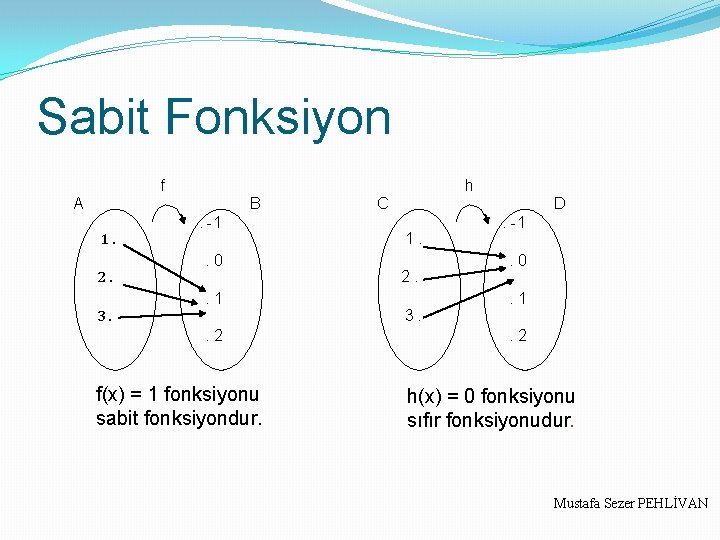
Sabit Fonksiyon Tanım kümesindeki bir bütün elemanları elemana değer eşleyen fonksiyona sabit fonksiyon denir. x A ve c B için, f(x) = c oluyorsa f, A dan B ye sabit fonksiyondur. c = 0 ve x A için, f(x) = 0 ise f fonksiyonu sıfır fonksiyonudur. Mustafa Sezer PEHLİVAN

Sabit Fonksiyon f h A B 1. 2. 3. . -1. 0. 1. 2 f(x) = 1 fonksiyonu sabit fonksiyondur. C D 1. 2. 3. . -1. 0. 1. 2 h(x) = 0 fonksiyonu sıfır fonksiyonudur. Mustafa Sezer PEHLİVAN

Tek ve Çift Fonksiyon f : R → R �f(-x) = f(x) ise, f fonksiyonu çift fonksiyondur. �f(-x) = -f(x) ise, f fonksiyonu tek fonksiyondur. Çift fonksiyonların grafikleri y eksenine göre simetriktir. Tek fonksiyonların grafikleri orijine göre simetriktir. Mustafa Sezer PEHLİVAN

Fonksiyonlarda Dört İşlem f ve g birer fonksiyon olsun. f : R → R g : R → R olmak üzere, f ± g(x): R → R (f ± g)(x) = f(x) ± g(x) Mustafa Sezer PEHLİVAN

Fonksiyonlarda Dört İşlem f. g(x): R → R (f. g)(x) = f(x). g(x) f/g (x): R → R f/g (x)=f(x)/g(x), (g(x)≠ 0) Burada dikkat edilmesi gereken noktalardan Ø Birincisi; işlemlerin sonucunun tanım kümesi, f ve g fonksiyonlarının tanım kümelerinin kesişim kümesidir, Ø ikincisi ise fonksiyonlar üzerinde tanımlanan işlemler fonksiyonların görüntü kümeleri üzerinde yapılacaktır. Mustafa Sezer PEHLİVAN

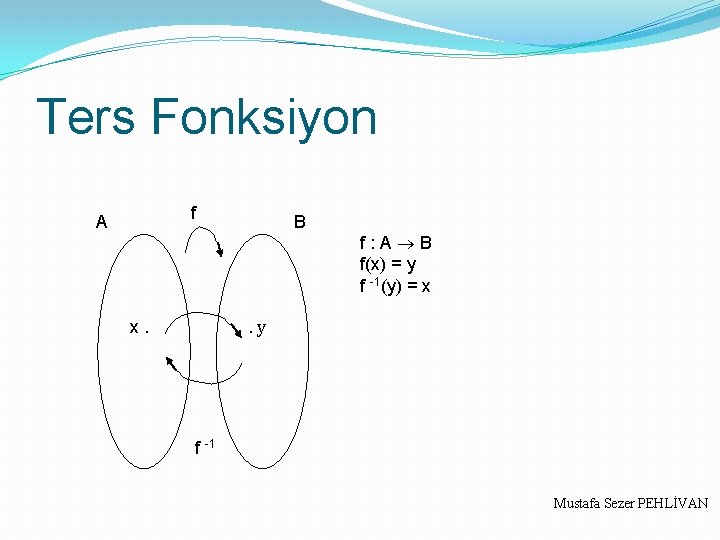
Ters Fonksiyon f : A B, f = {(x, y)|x A, y B} bire bir ve örten fonksiyon olmak üzere, f– 1 : B A, f– 1 = {(y, x)|(x, y) f} fonksiyonuna f nin ters fonksiyonu denir ve f– 1(x) ile gösterilir. Mustafa Sezer PEHLİVAN

Ters Fonksiyon f A B f : A B f(x) = y f -1(y) = x. y x. f -1 Mustafa Sezer PEHLİVAN

Ters Fonksiyon (x, y) f ise, (y, x) f– 1 olduğu için, y = f(x) ise, x = f– 1(y) dir. Ayrıca, (f– 1)– 1 = f dir. Ancak, (f– 1(x))– 1 ≠ f(x) tir. f fonksiyonu bire bir ve örten değilse, f– 1 fonksiyon değildir. f : A B ise, f– 1 : B A olduğu için, f nin tanım kümesi, f– 1 in değer kümesidir. f nin değer kümesi de, f– 1 in tanım kümesidir. f(a) = b ise, f– 1(b) = a dır. f– 1(b) = a ise, f(a) = b dir. Mustafa Sezer PEHLİVAN

Ters Fonksiyon y = f(x) fonksiyonunun grafiği ile y = f– 1(x) in grafiği y = x doğrusuna göre birbirinin simetriğidir. Mustafa Sezer PEHLİVAN

y = f(x) x = f -1 (y) olduğundan f -1 i bulmak için x, y cinsinden bulunur ve x ile y nin yerleri değiştirilir. Örnek: f : R R, f(x) olduğuna göre f -1 i bulalım. y 3 x + 2 = 4 y 3 x = 4 y - 2 x f: R R f: x y f(x) =y f -1 (x) olur. Mustafa Sezer PEHLİVAN

Bileşke Fonksiyon f g f : A B, g : B C fonksiyonları tanımlansın. f ve B C A g yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f x. . z. y nin bileşke fonksiyonu denir ve gof(x)=g(f(x)) şeklinde gösterilir. gof Mustafa Sezer PEHLİVAN

Bileşke Fonksiyon Bileşke fonksiyonların özellikleri • Bileşke işleminin değişme özeliği yoktur. Bu durumda, fog ≠ gof dir. • Bazı fonksiyonlar için fog = gof olabilir. Ancak bu “fonksiyonlarda değişme özeliği yoktur. ” gerçeğini değiştirmez. • Fonksiyonlarda bileşke işleminin birleşme özeliği vardır. • Bu durumda (fog)oh = fo(goh) = fogoh olur. Mustafa Sezer PEHLİVAN

SORU 1: Mustafa Sezer PEHLİVAN

SORU 2: Mustafa Sezer PEHLİVAN

SORU 3: Mustafa Sezer PEHLİVAN

SORU 4: Mustafa Sezer PEHLİVAN

� Mustafa Sezer PEHLİVAN

� Mustafa Sezer PEHLİVAN

� Mustafa Sezer PEHLİVAN