Linear filters What is Image Filtering Modify the

Linear filters

What is Image Filtering? Modify the pixels in an image based on some function of a local neighborhood of the pixels 10 5 4 5 1 1 CS 8690 Computer Vision 3 1 7 Some function 7 University of Missouri at Columbia

Linear Filtering • Linear case is simplest and most useful – Replace each pixel with a linear combination of its neighbors. • The prescription for the linear combination is called the convolution kernel. 10 5 3 0 0 0 4 5 1 0 0. 5 0 1 1 7 0 1. 0 0. 5 7 kernel CS 8690 Computer Vision University of Missouri at Columbia

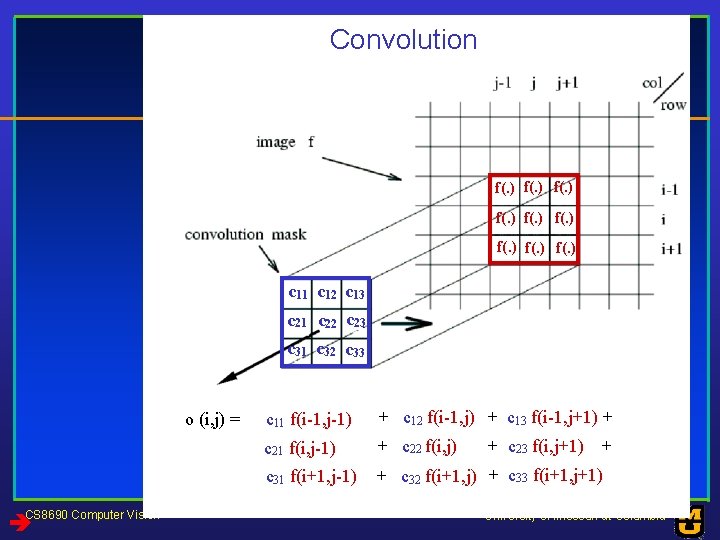
Convolution f(. ) f(. ) c 11 c 12 c 13 c 21 c 22 c 23 c 31 c 32 c 33 o (i, j) = CS 8690 Computer Vision c 11 f(i-1, j-1) + c 12 f(i-1, j) + c 13 f(i-1, j+1) + c 21 f(i, j-1) + c 22 f(i, j) c 31 f(i+1, j-1) + c 32 f(i+1, j) + c 33 f(i+1, j+1) + c 23 f(i, j+1) + University of Missouri at Columbia

Linear Filter = Convolution CS 8690 Computer Vision University of Missouri at Columbia

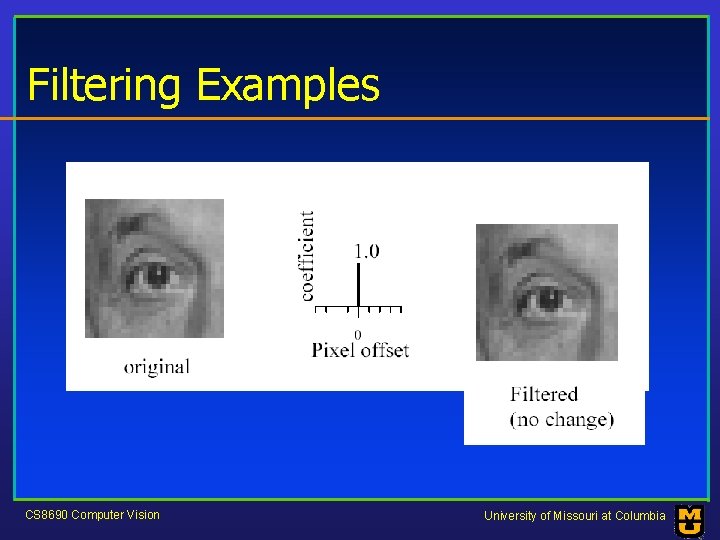
Filtering Examples CS 8690 Computer Vision University of Missouri at Columbia

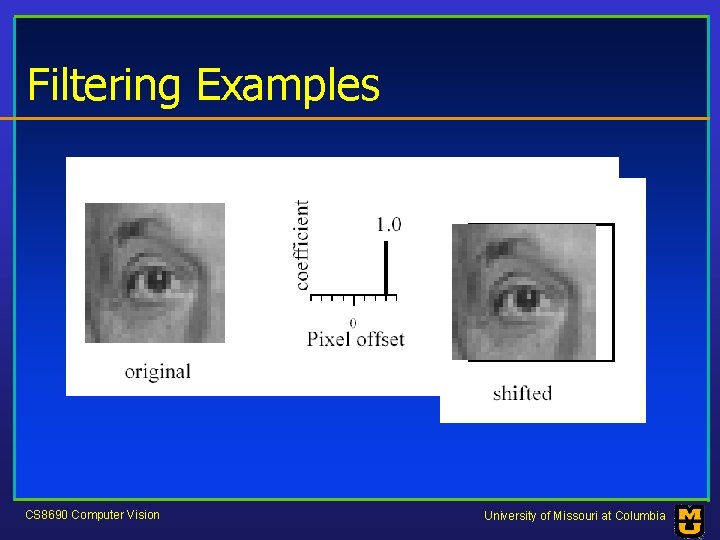
Filtering Examples CS 8690 Computer Vision University of Missouri at Columbia

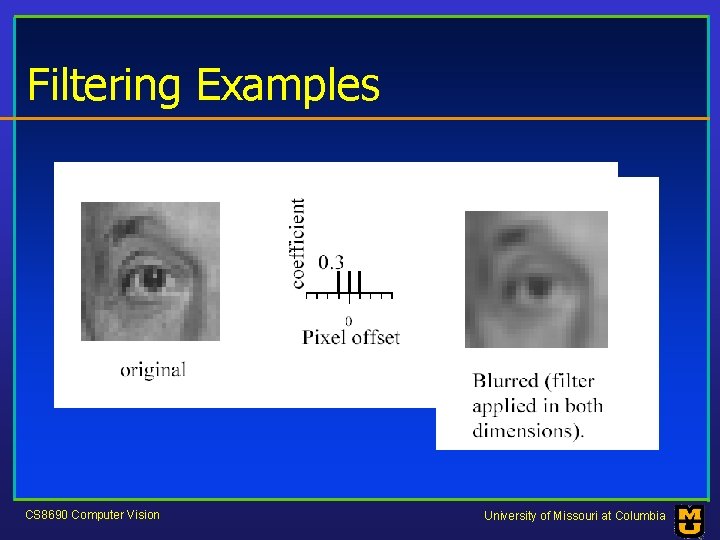
Filtering Examples CS 8690 Computer Vision University of Missouri at Columbia

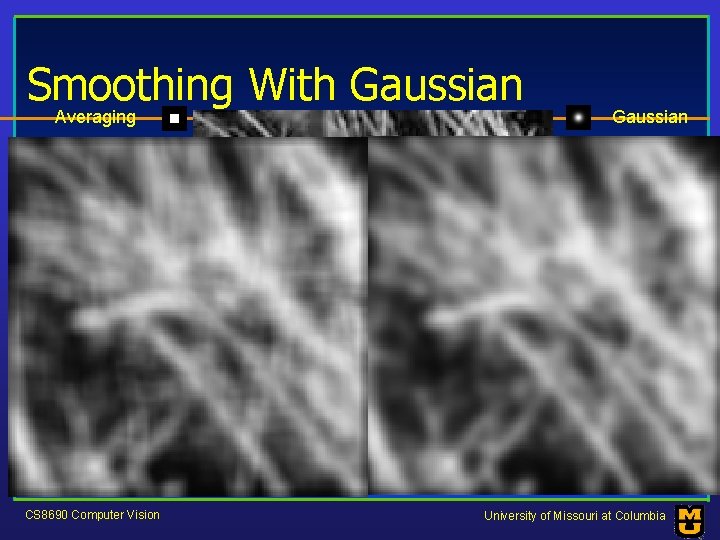
Smoothing With Gaussian Averaging CS 8690 Computer Vision Gaussian University of Missouri at Columbia

Linear Filters • General process: – Form new image whose pixels are a weighted sum of original pixel values, using the same set of weights at each point. • Properties – Output is a linear function of the input – Output is a shift-invariant function of the input (i. e. shift the input image two pixels to the left, the output is shifted two pixels to the left) CS 8690 Computer Vision • Example: smoothing by averaging – form the average of pixels in a neighbourhood • Example: smoothing with a Gaussian – form a weighted average of pixels in a neighbourhood • Example: finding a derivative – form a weighted average of pixels in a neighbourhood University of Missouri at Columbia

Convolution • Represent these weights as an image, H • H is usually called the kernel • Operation is called convolution – it’s associative CS 8690 Computer Vision • Result is: • Notice wierd order of indices – all examples can be put in this form – it’s a result of the derivation expressing any shift-invariant linear operator as a convolution. University of Missouri at Columbia

Example: Smoothing by Averaging CS 8690 Computer Vision University of Missouri at Columbia

Smoothing with a Gaussian • Smoothing with an average actually doesn’t compare at all well with a defocussed lens – Most obvious difference is that a single point of light viewed in a defocussed lens looks like a fuzzy blob; but the averaging process would give a little • A Gaussian gives a good model of a fuzzy blob square. CS 8690 Computer Vision University of Missouri at Columbia

An Isotropic Gaussian • The picture shows a smoothing kernel proportional to (which is a reasonable model of a circularly symmetric fuzzy blob) CS 8690 Computer Vision University of Missouri at Columbia

Differentiation and convolution • Recall • We could approximate this as (which is obviously a • Now this is linear and convolution; it’s not a shift invariant, so must be very good way to do the result of a things, as we shall see) convolution. CS 8690 Computer Vision University of Missouri at Columbia

Finite differences CS 8690 Computer Vision University of Missouri at Columbia

Noise • Simplest noise model – independent stationary additive Gaussian noise – the noise value at each pixel is given by an independent draw from the same normal probability distribution CS 8690 Computer Vision • Issues – this model allows noise values that could be greater than maximum camera output or less than zero – for small standard deviations, this isn’t too much of a problem - it’s a fairly good model – independence may not be justified (e. g. damage to lens) – may not be stationary (e. g. thermal gradients in the ccd) University of Missouri at Columbia

sigma=1 CS 8690 Computer Vision University of Missouri at Columbia

sigma=16 CS 8690 Computer Vision University of Missouri at Columbia

Finite differences and noise • Finite difference filters respond strongly to noise – obvious reason: image noise results in pixels that look very different from their neighbours • Generally, the larger the noise the stronger the response CS 8690 Computer Vision • What is to be done? – intuitively, most pixels in images look quite a lot like their neighbours – this is true even at an edge; along the edge they’re similar, across the edge they’re not – suggests that smoothing the image should help, by forcing pixels different to their neighbours (=noise pixels? ) to look more like neighbours University of Missouri at Columbia

Finite differences responding to noise Increasing noise -> (this is zero mean additive gaussian noise) CS 8690 Computer Vision University of Missouri at Columbia

The response of a linear filter to noise • Do only stationary independent additive Gaussian noise with zero mean (non-zero mean is easily dealt with) • Mean: – output is a weighted sum of inputs – so we want mean of a weighted sum of zero mean normal random variables – must be zero CS 8690 Computer Vision • Variance: – recall • variance of a sum of random variables is sum of their variances • variance of constant times random variable is constant^2 times variance – then if s is noise variance and kernel is K, variance of response is University of Missouri at Columbia

Filter responses are correlated • over scales similar to the scale of the filter • Filtered noise is sometimes useful – looks like some natural textures, can be used to simulate fire, etc. CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

Smoothing reduces noise • Generally expect pixels to “be like” their neighbours – surfaces turn slowly – relatively few reflectance changes • Generally expect noise processes to be independent from pixel to pixel CS 8690 Computer Vision • Implies that smoothing suppresses noise, for appropriate noise models • Scale – the parameter in the symmetric Gaussian – as this parameter goes up, more pixels are involved in the average – and the image gets more blurred – and noise is more effectively suppressed University of Missouri at Columbia

The effects of smoothing Each row shows smoothing with gaussians of different width; each column shows different realisations of an image of gaussian noise. CS 8690 Computer Vision University of Missouri at Columbia

Some other useful filtering techniques • Median filter • Anisotropic diffusion CS 8690 Computer Vision University of Missouri at Columbia

Median filters : principle non-linear filter method : n 1. rank-order neighbourhood intensities n 2. take middle value no new grey levels emerge. . . CS 8690 Computer Vision University of Missouri at Columbia

Median filters : odd-man-out advantage of this type of filter is its “odd-man-out” effect e. g. 1, 1, 1, 7, 1, 1 ? , 1, 1, 1, ? CS 8690 Computer Vision University of Missouri at Columbia

Median filters : example filters have width 5 : CS 8690 Computer Vision University of Missouri at Columbia

Median filters : analysis median completely discards the spike, linear filter always responds to all aspects median filter preserves discontinuities, linear filter produces rounding-off effects DON’T become all too optimistic CS 8690 Computer Vision University of Missouri at Columbia

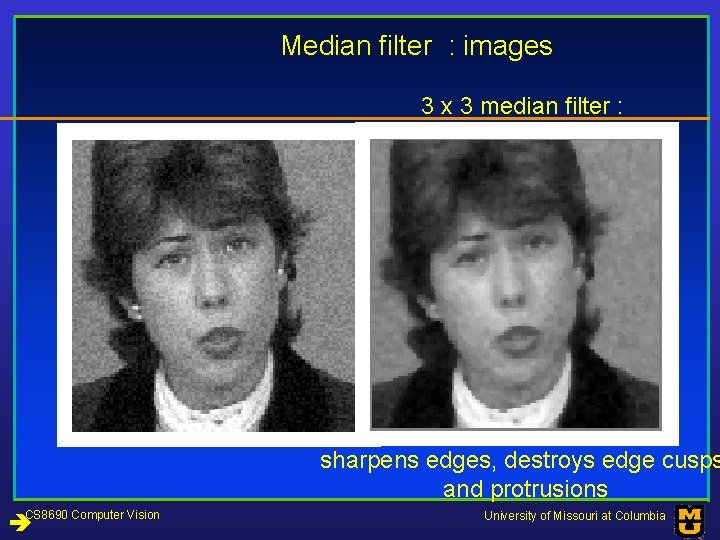
Median filter : images 3 x 3 median filter : sharpens edges, destroys edge cusps and protrusions CS 8690 Computer Vision University of Missouri at Columbia

Median filters : Gauss revisited 3 x 3 median filter : sharpens edges, destroys edge cusps and protrusions CS 8690 Computer Vision Comparison with Gaussian : e. g. upper lip smoother, eye better preserved University of Missouri at Columbia

Example of median 10 times 3 X 3 median CS 8690 Computer Vision patchy effect important details lost (e. g. ear-ring) University of Missouri at Columbia

Pyramids

Linear filters Gaussian blurring Finite differences Composition of linear filters = linear filter Edge detection CS 8690 Computer Vision Corners, etc. University of Missouri at Columbia

Scaled representations • Big bars (resp. spots, hands, etc. ) and little bars are both interesting – Stripes and hairs, say • Inefficient to detect big bars with big filters – And there is superfluous detail in the filter kernel CS 8690 Computer Vision • Alternative: – Apply filters of fixed size to images of different sizes – Typically, a collection of images whose edge length changes by a factor of 2 (or root 2) – This is a pyramid (or Gaussian pyramid) by visual analogy University of Missouri at Columbia

A bar in the big images is a hair on the zebra’s nose; in smaller images, a stripe; in the smallest, the animal’s nose CS 8690 Computer Vision University of Missouri at Columbia

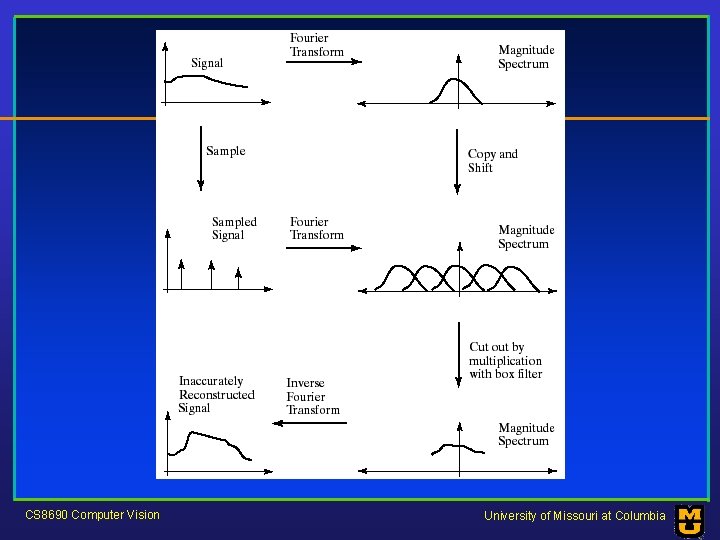
Aliasing • Can’t shrink an image by taking every second pixel • If we do, characteristic errors appear – In the next few slides – Typically, small phenomena look bigger; fast phenomena can look slower – Common phenomenon • Wagon wheels rolling the wrong way in movies • Checkerboards misrepresented in ray tracing • Striped shirts look funny on colour television CS 8690 Computer Vision University of Missouri at Columbia

Resample the checkerboard by taking one sample at each circle. In the case of the top left board, new representation is reasonable. Top right also yields a reasonable representation. Bottom left is all black (dubious) and bottom right has checks that are too big. CS 8690 Computer Vision University of Missouri at Columbia

Constructing a pyramid by taking every second pixel leads to layers that badly misrepresent the top layer CS 8690 Computer Vision University of Missouri at Columbia

Open questions • What causes the tendency of differentiation to emphasize noise? • In what precise respects are discrete images different from continuous images? • How do we avoid aliasing? • General thread: a language for fast changes The Fourier Transform CS 8690 Computer Vision University of Missouri at Columbia

The Fourier Transform • Represent function on a new basis – Think of functions as vectors, with many components – We now apply a linear transformation to transform the basis • dot product with each basis element • In the expression, u and v select the basis element, so a function of x and y becomes a function of u and v • basis elements have the form transformed image vectorized image Fourier transform base, . CS 8690 Computer Vision University of Missouri at Columbia

To get some sense of what basis elements look like, we plot a basis element --- or rather, its real part --as a function of x, y for some fixed u, v. We get a function that is constant when (ux+vy) is constant. The magnitude of the vector (u, v) gives a frequency, and its direction gives an orientation. The function is a sinusoid with this frequency along the direction, and constant perpendicular to the direction. CS 8690 Computer Vision University of Missouri at Columbia

Fourier basis element example, real part Fu, v(x, y)=const. for (ux+vy)=const. Vector (u, v) • Magnitude gives frequency • Direction gives orientation. CS 8690 Computer Vision University of Missouri at Columbia

Here u and v are larger than in the previous slide. CS 8690 Computer Vision University of Missouri at Columbia

And larger still. . . CS 8690 Computer Vision University of Missouri at Columbia

Phase and Magnitude • Fourier transform of a real function is complex – difficult to plot, visualize – instead, we can think of the phase and magnitude of the transform • Phase is the phase of the complex transform • Magnitude is the magnitude of the complex transform CS 8690 Computer Vision • Curious fact – all natural images have about the same magnitude transform – hence, phase seems to matter, but magnitude largely doesn’t • Demonstration – Take two pictures, swap the phase transforms, compute the inverse - what does the result look like? University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

This is the magnitude transform of the cheetah pic CS 8690 Computer Vision University of Missouri at Columbia

This is the phase transform of the cheetah pic CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

This is the magnitude transform of the zebra pic CS 8690 Computer Vision University of Missouri at Columbia

This is the phase transform of the zebra pic CS 8690 Computer Vision University of Missouri at Columbia

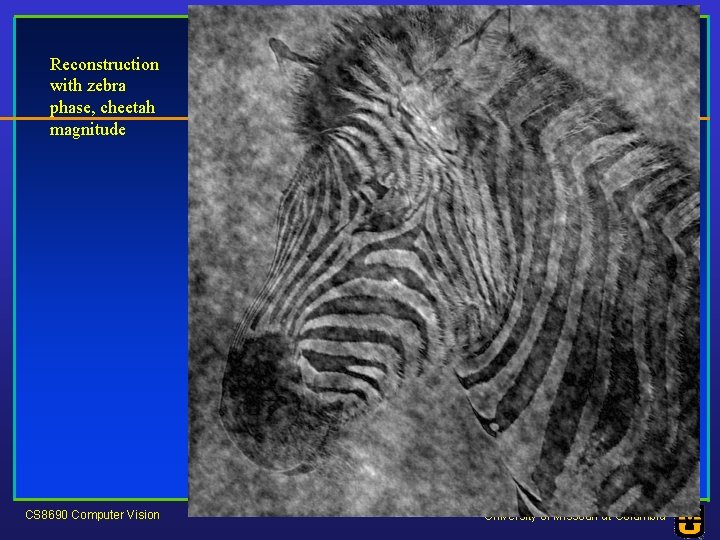
Reconstruction with zebra phase, cheetah magnitude CS 8690 Computer Vision University of Missouri at Columbia

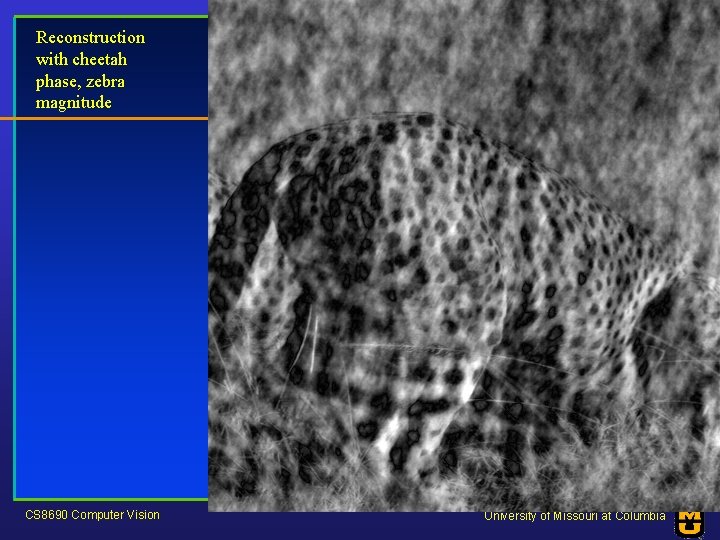
Reconstruction with cheetah phase, zebra magnitude CS 8690 Computer Vision University of Missouri at Columbia

Various Fourier Transform Pairs • Important facts – The Fourier transform is linear – There is an inverse FT – scale function down scale transform up i. e. high frequency = small details – The FT of a Gaussian is a Gaussian. compare to box function transform CS 8690 Computer Vision University of Missouri at Columbia

Convolution theorem • The convolution theorem – The Fourier transform of the convolution of two functions is the product of their Fourier transforms – The Fourier transform of the product of two functions is the convolution of the Fourier transforms CS 8690 Computer Vision University of Missouri at Columbia

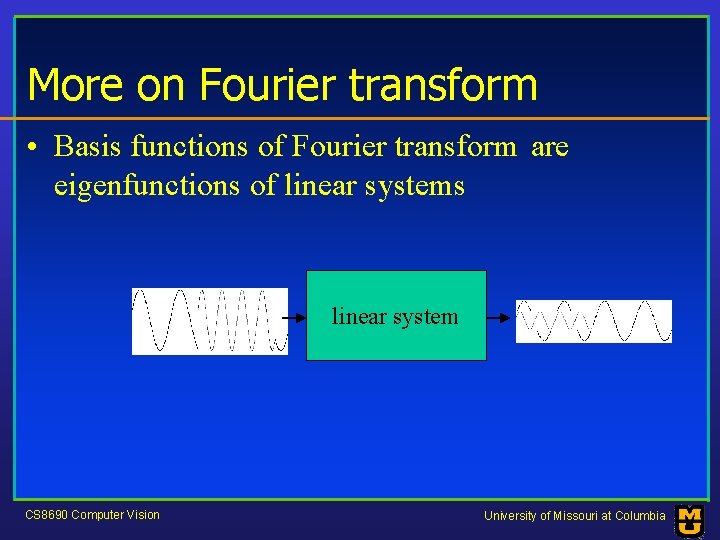
More on Fourier transform • Basis functions of Fourier transform are eigenfunctions of linear systems linear system CS 8690 Computer Vision University of Missouri at Columbia

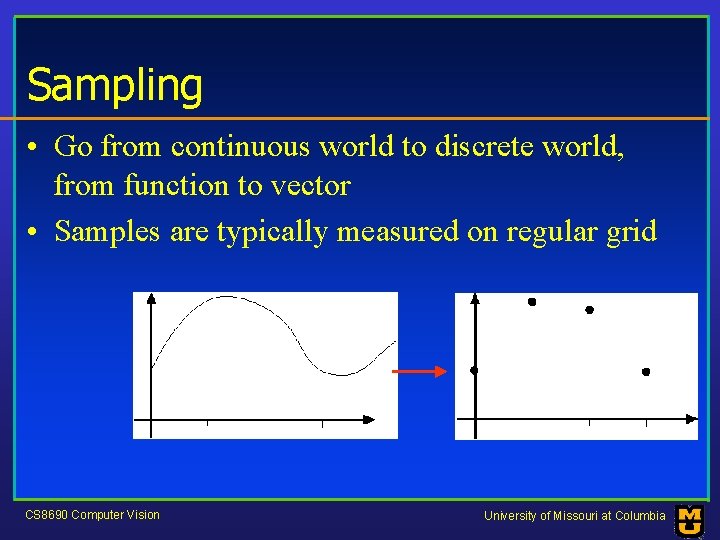
Sampling • Go from continuous world to discrete world, from function to vector • Samples are typically measured on regular grid CS 8690 Computer Vision University of Missouri at Columbia

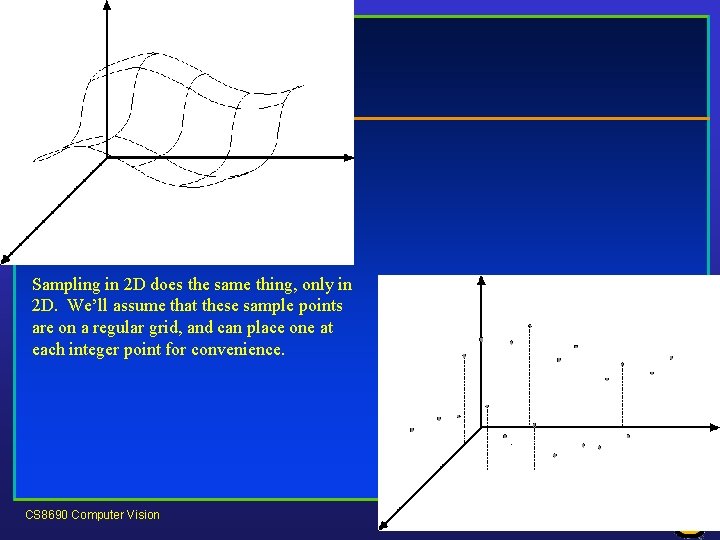
Sampling in 2 D does the same thing, only in 2 D. We’ll assume that these sample points are on a regular grid, and can place one at each integer point for convenience. CS 8690 Computer Vision University of Missouri at Columbia

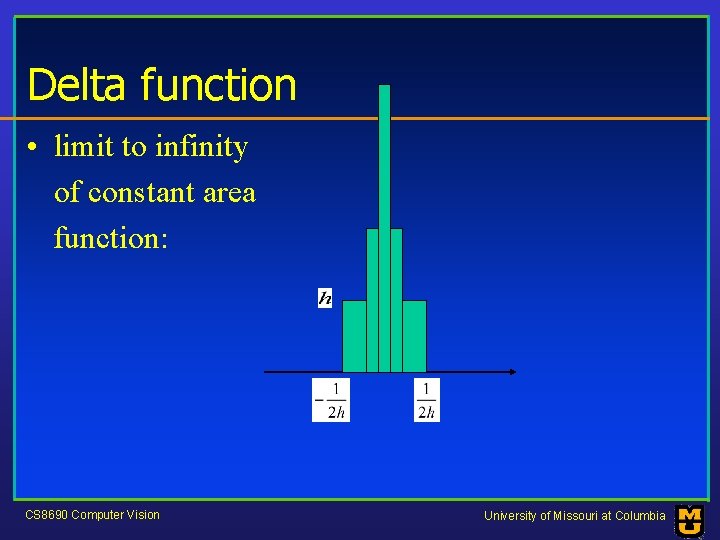
Delta function • limit to infinity of constant area function: CS 8690 Computer Vision University of Missouri at Columbia

A continuous model for a sampled function • We want to be able to approximate integrals sensibly • Leads to – the delta function – model on right CS 8690 Computer Vision University of Missouri at Columbia

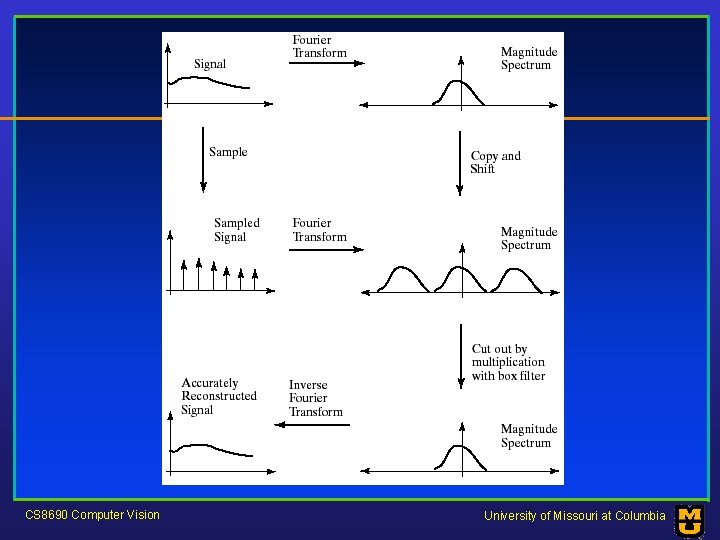
The Fourier transform of a sampled signal CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

Smoothing as low-pass filtering • The message of the FT is that high frequencies lead to trouble with sampling. • Solution: suppress high frequencies before sampling – multiply the FT of the signal with something that suppresses high frequencies – or convolve with a lowpass filter CS 8690 Computer Vision • A filter whose FT is a box is bad, because the filter kernel has infinite support • Common solution: use a Gaussian – multiplying FT by Gaussian is equivalent to convolving image with Gaussian. University of Missouri at Columbia

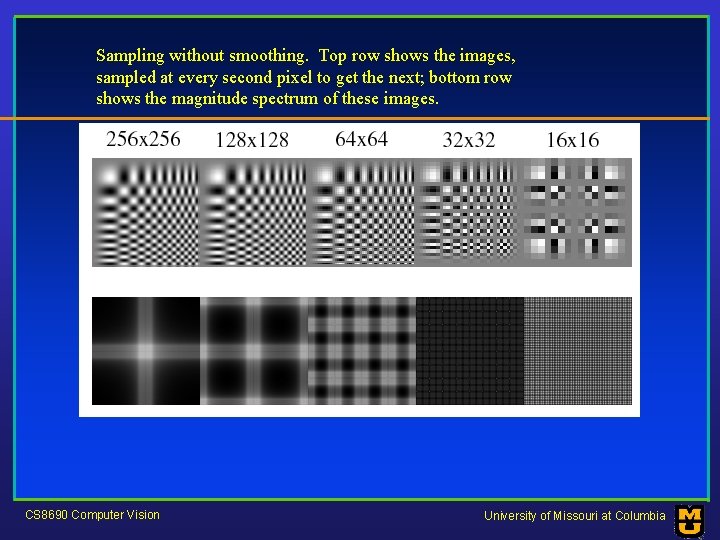
Sampling without smoothing. Top row shows the images, sampled at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. CS 8690 Computer Vision University of Missouri at Columbia

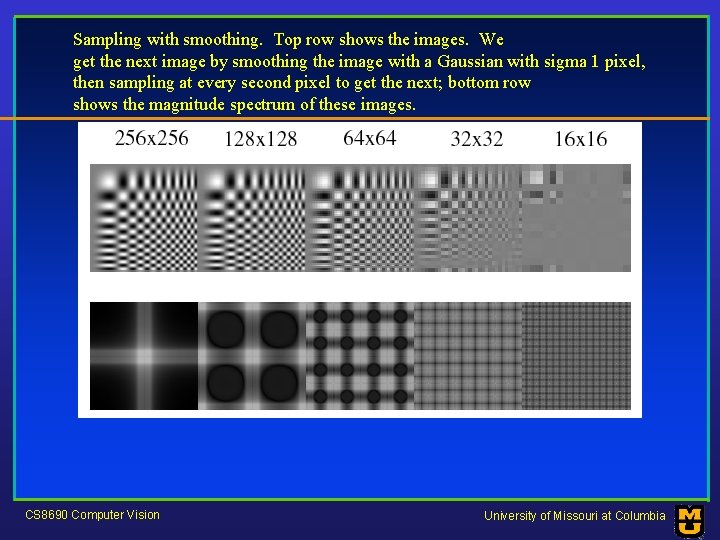
Sampling with smoothing. Top row shows the images. We get the next image by smoothing the image with a Gaussian with sigma 1 pixel, then sampling at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. CS 8690 Computer Vision University of Missouri at Columbia

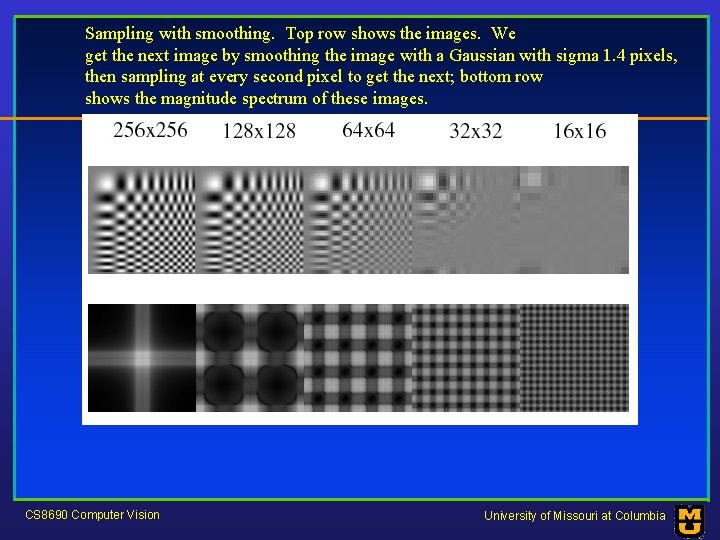
Sampling with smoothing. Top row shows the images. We get the next image by smoothing the image with a Gaussian with sigma 1. 4 pixels, then sampling at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. CS 8690 Computer Vision University of Missouri at Columbia

Applications of scaled representations • Search for correspondence – look at coarse scales, then refine with finer scales • Edge tracking – a “good” edge at a fine scale has parents at a coarser scale • Control of detail and computational cost in matching – e. g. finding stripes – terribly important in texture representation CS 8690 Computer Vision University of Missouri at Columbia

Gaussian Pyramid Gaussian Image Filter Downsample Low-Pass Filtered Image Low-Res Image

The Gaussian pyramid • Smooth with gaussians, because – a gaussian*gaussian=another gaussian • Synthesis – smooth and sample • Analysis – take the top image • Gaussians are low pass filters, so representation is redundant CS 8690 Computer Vision University of Missouri at Columbia

Example: CMU face detection CS 8690 Computer Vision University of Missouri at Columbia

The Gaussian pyramid CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia http: //web. mit. edu/persci/people/adelson/pub_pdfs/pyramid 83. pdf