Recap of Friday linear Filtering convolution differential filters

Recap of Friday linear Filtering convolution differential filters filter types boundary conditions.

Review: questions 1. Write down a 3 x 3 filter that returns a positive value if the average value of the 4 -adjacent neighbors is less than the center and a negative value otherwise 2. Write down a filter that will compute the gradient in the x-direction: gradx(y, x) = im(y, x+1)-im(y, x) for each x, y Slide: Hoiem

Review: questions 3. Fill in the blanks: a) b) c) d) _ A F _ = = D _ D D * * Filtering Operator B A _ _ D B E G C F H I D Slide: Hoiem

The Frequency Domain (Szeliski 3. 4) Somewhere in Cinque Terre, May 2005 Slides from Steve Seitz and Alexei Efros CS 129: Computational Photography James Hays, Brown, Spring 2011

Salvador Dali “Gala Contemplating the Mediterranean Sea, which at 30 meters becomes the portrait of Abraham Lincoln”, 1976

A nice set of basis Teases away fast vs. slow changes in the image. This change of basis has a special name…

Jean Baptiste Joseph Fourier (1768 -1830) had crazy idea (1807): Any periodic function can be rewritten as a weighted sum of sines and cosines of different frequencies. Don’t believe it? • Neither did Lagrange, Laplace, Poisson and other big wigs • Not translated into English until 1878! But it’s true! • called Fourier Series

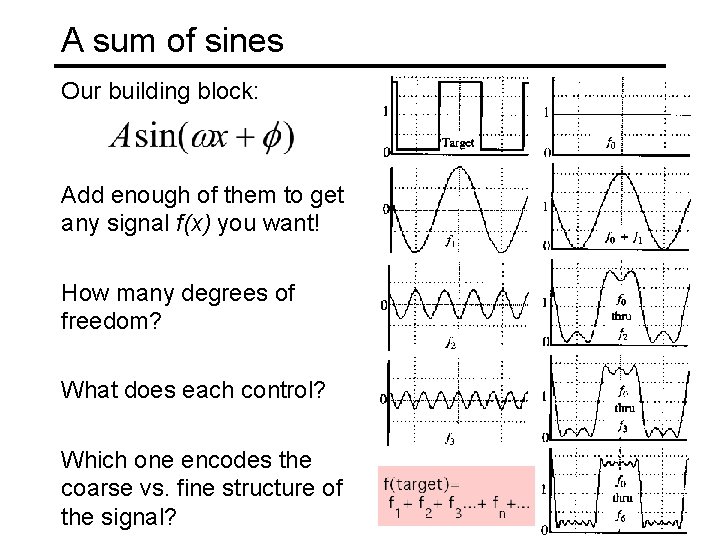
A sum of sines Our building block: Add enough of them to get any signal f(x) you want! How many degrees of freedom? What does each control? Which one encodes the coarse vs. fine structure of the signal?

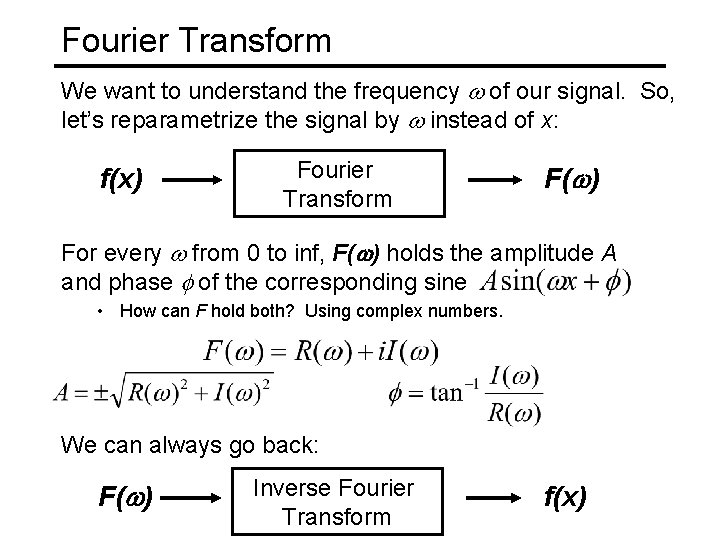
Fourier Transform We want to understand the frequency w of our signal. So, let’s reparametrize the signal by w instead of x: f(x) Fourier Transform F(w) For every w from 0 to inf, F(w) holds the amplitude A and phase f of the corresponding sine • How can F hold both? Using complex numbers. We can always go back: F(w) Inverse Fourier Transform f(x)

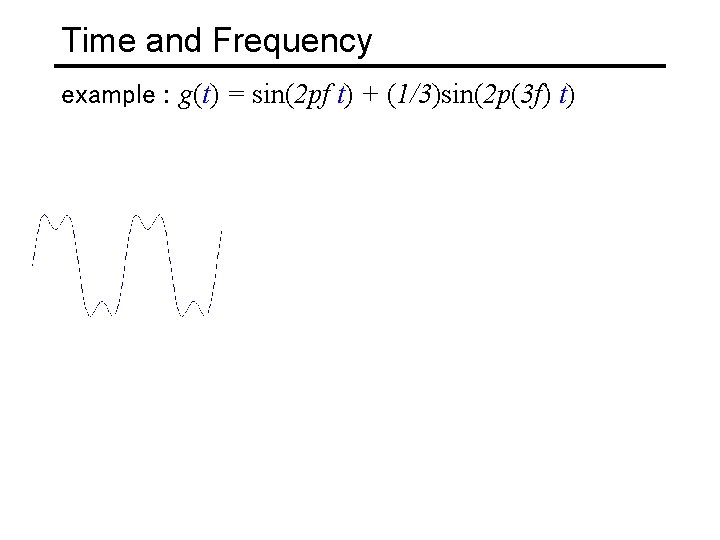
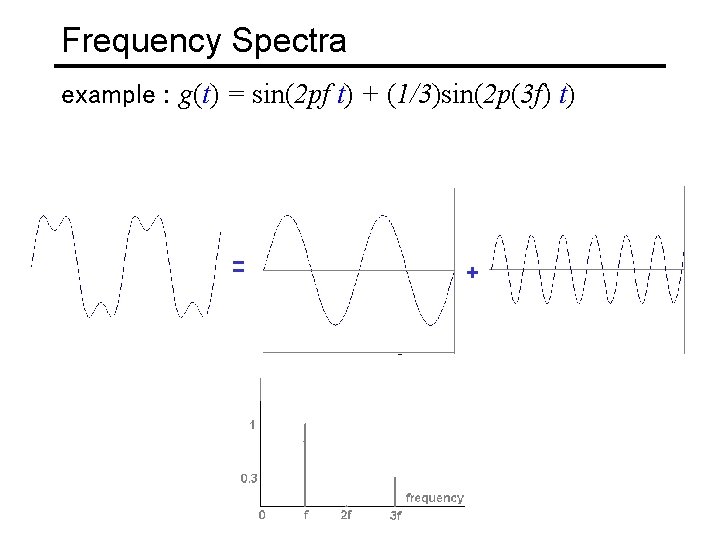
Time and Frequency example : g(t) = sin(2 pf t) + (1/3)sin(2 p(3 f) t)

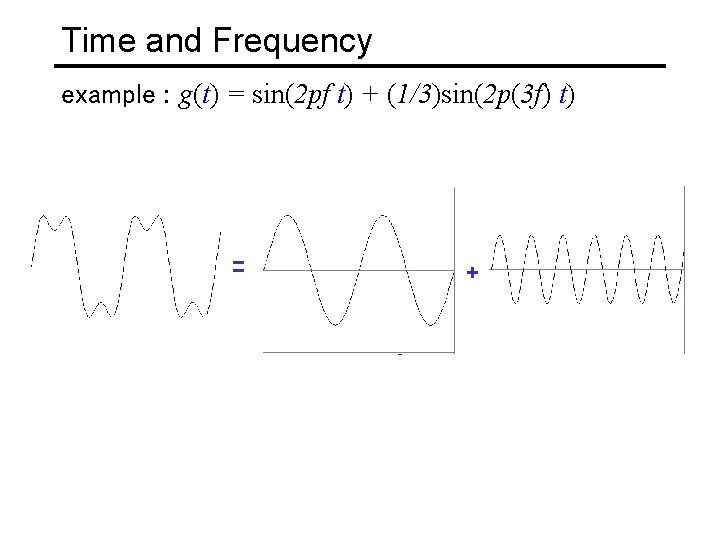
Time and Frequency example : g(t) = sin(2 pf t) + (1/3)sin(2 p(3 f) t) = +

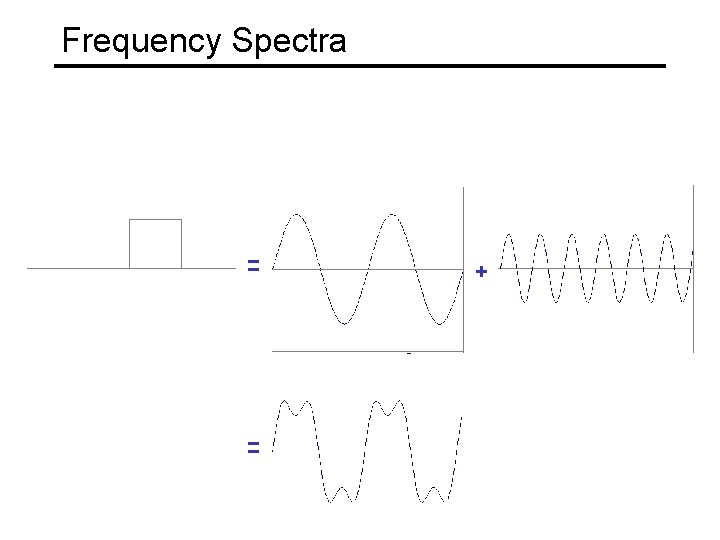
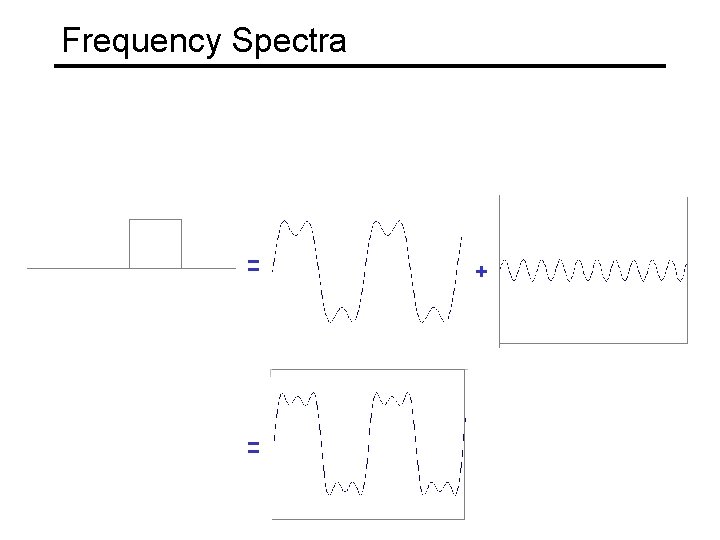
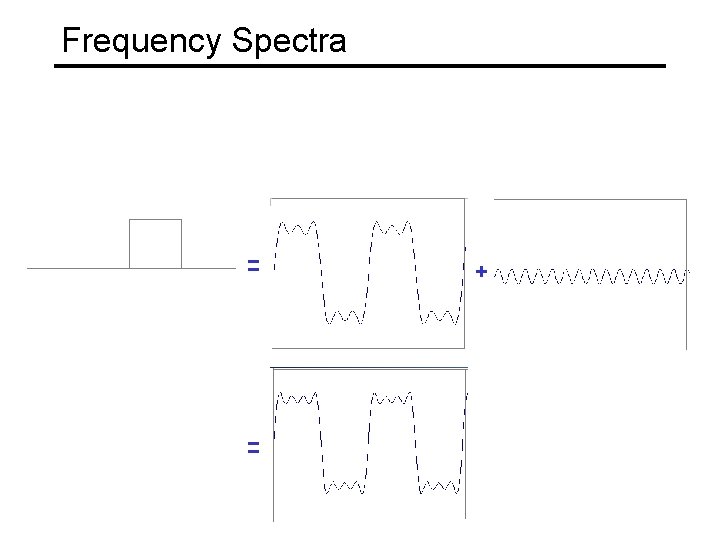
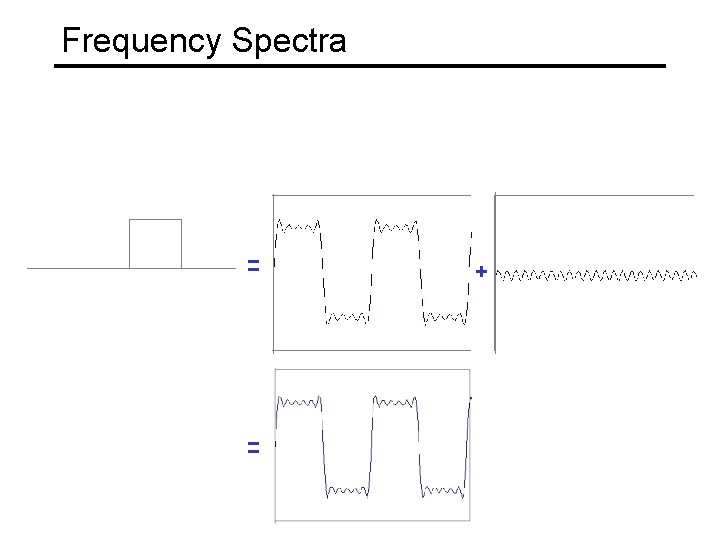
Frequency Spectra example : g(t) = sin(2 pf t) + (1/3)sin(2 p(3 f) t) = +

Frequency Spectra Usually, frequency is more interesting than the phase

Frequency Spectra = = +

Frequency Spectra = = +

Frequency Spectra = = +

Frequency Spectra = = +

Frequency Spectra = = +

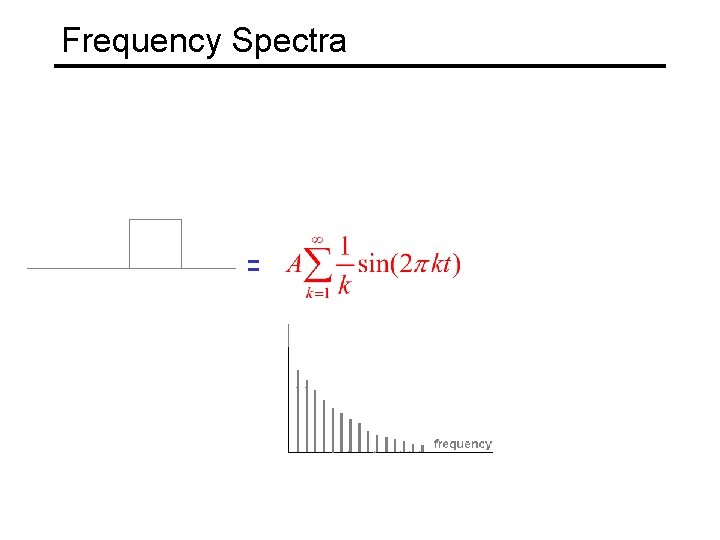
Frequency Spectra =

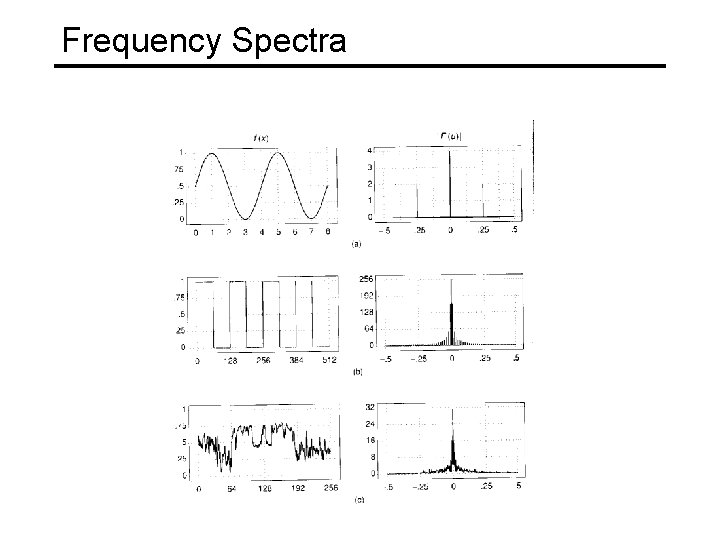
Frequency Spectra

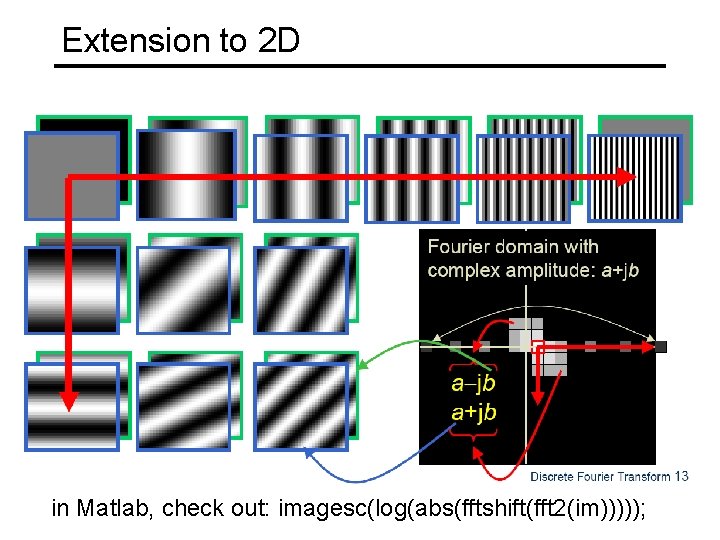
Extension to 2 D in Matlab, check out: imagesc(log(abs(fftshift(fft 2(im)))));

Man-made Scene

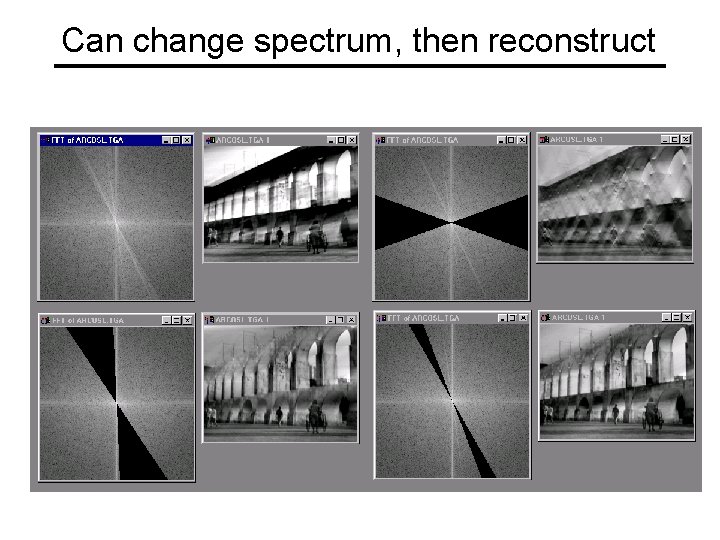
Can change spectrum, then reconstruct

Low and High Pass filtering

The Convolution Theorem • The Fourier transform of the convolution of two functions is the product of their Fourier transforms • Convolution in spatial domain is equivalent to multiplication in frequency domain!

2 D convolution theorem example |F(sx, sy)| f(x, y) * h(x, y) |H(sx, sy)| g(x, y) |G(sx, sy)|

Filtering in frequency domain FFT = Inverse FFT Slide: Hoiem

FFT in Matlab • Filtering with fft im = double(imread(‘…'))/255; im = rgb 2 gray(im); % “im” should be a gray-scale floating point image [imh, imw] = size(im); hs = 50; % filter half-size fil = fspecial('gaussian', hs*2+1, 10); fftsize = 1024; % should be order of 2 (for speed) and include im_fft = fft 2(im, fftsize); % 1) fil_fft = fft 2(fil, fftsize); % 2) image im_fil_fft = im_fft. * fil_fft; % 3) im_fil = ifft 2(im_fil_fft); % 4) im_fil = im_fil(1+hs: size(im, 1)+hs, 1+hs: size(im, 2)+hs); % 5) padding fft im with padding fft fil, pad to same size as multiply fft images inverse fft 2 remove padding • Displaying with fft figure(1), imagesc(log(abs(fftshift(im_fft)))), axis image, colormap jet Slide: Hoiem

Fourier Transform pairs

Low-pass, Band-pass, High-pass filters low-pass: High-pass / band-pass:

Edges in images

What does blurring take away? original

What does blurring take away? smoothed (5 x 5 Gaussian)

High-Pass filter smoothed – original

Image gradient The gradient of an image: The gradient points in the direction of most rapid change in intensity The gradient direction is given by: • how does this relate to the direction of the edge? The edge strength is given by the gradient magnitude

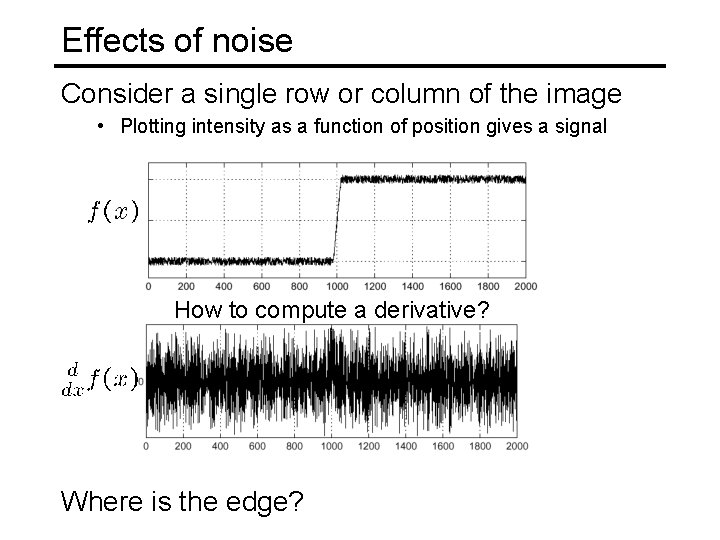
Effects of noise Consider a single row or column of the image • Plotting intensity as a function of position gives a signal How to compute a derivative? Where is the edge?

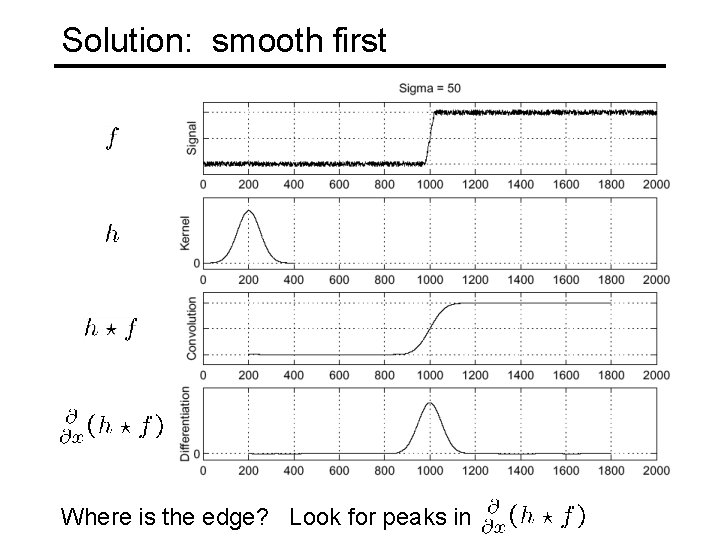
Solution: smooth first Where is the edge? Look for peaks in

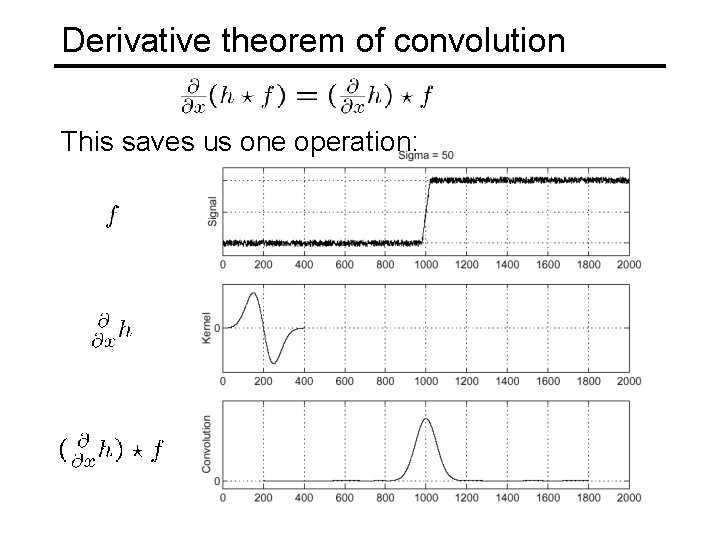
Derivative theorem of convolution This saves us one operation:

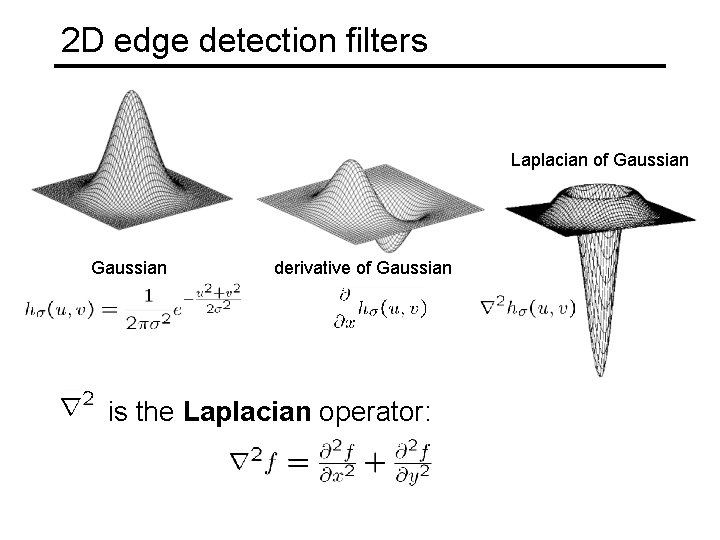
2 D edge detection filters Laplacian of Gaussian derivative of Gaussian is the Laplacian operator:

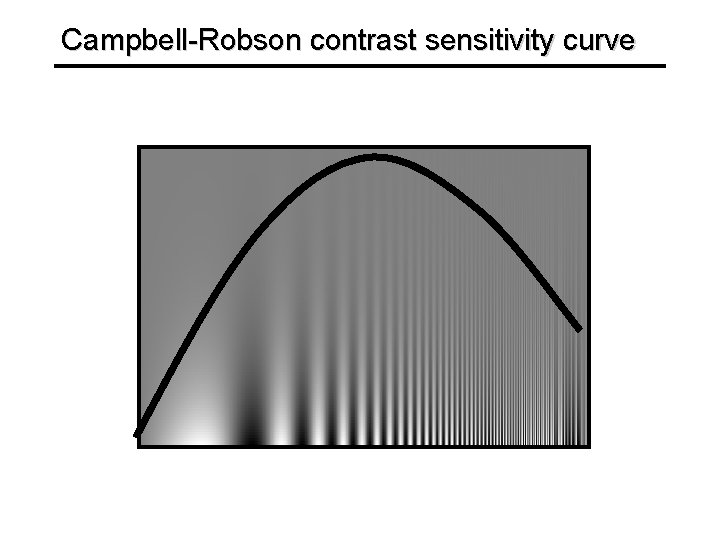
Campbell-Robson contrast sensitivity curve

Depends on Color R G B

Lossy Image Compression (JPEG) Block-based Discrete Cosine Transform (DCT)

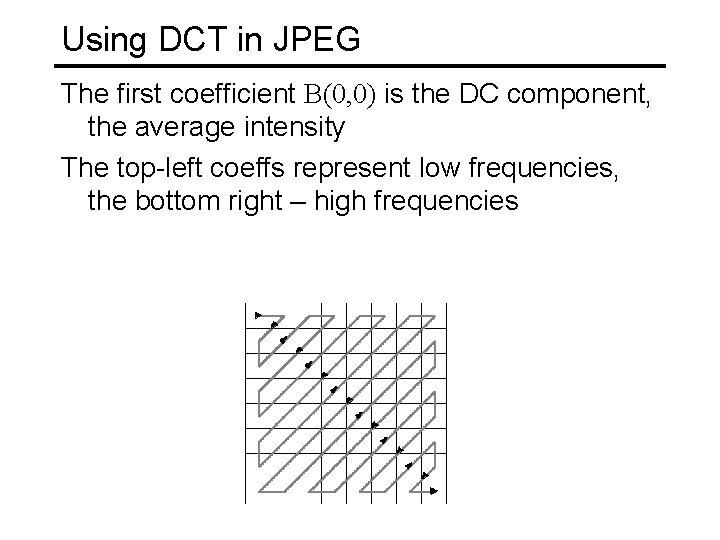
Using DCT in JPEG The first coefficient B(0, 0) is the DC component, the average intensity The top-left coeffs represent low frequencies, the bottom right – high frequencies

Image compression using DCT enables image compression by concentrating most image information in the low frequencies Lose unimportant image info (high frequencies) by cutting B(u, v) at bottom right The decoder computes the inverse DCT – IDCT • Quantization Table 3 5 7 9 11 13 15 17 19 21 23 11 13 15 17 19 21 23 25 27 29 31

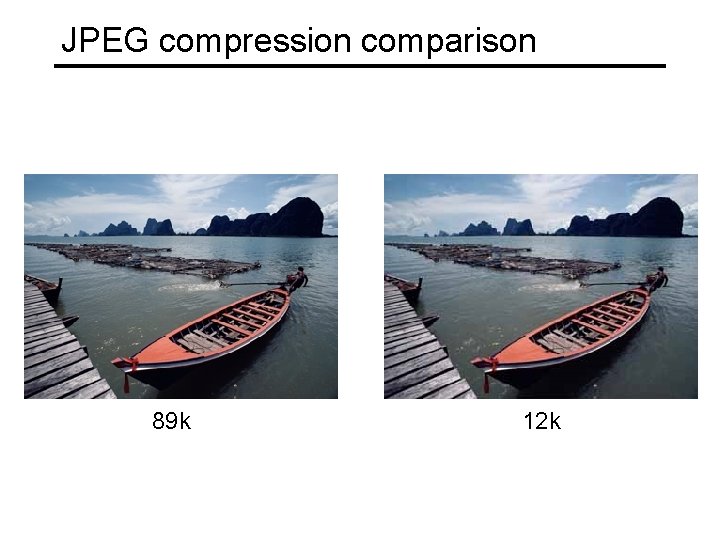
JPEG compression comparison 89 k 12 k

Things to Remember Sometimes it makes sense to think of images and filtering in the frequency domain • Fourier analysis Can be faster to filter using FFT for large images (N log. N vs. N 2 for autocorrelation) Images are mostly smooth • Basis for compression Remember to low-pass before sampling

Summary Frequency domain can be useful for Analysis Computational efficiency Compression