Lecture 5 Determinants Lat Time Elementary Matrices n

Lecture 5 Determinants Lat Time Elementary Matrices n. Determinant of a Matrix n. Evaluation of Determinant Reading Assignment: Secs 2. 4, 3. 1, 3. 2 of Textbook n Elementary Linear Algebra R. Larsen et al. (5 Edition) TKUEE翁慶昌-NTUEE SCC_09_2007

Lecture 5: Determinants Today n Matrix Computation Packages (Matlab and …) n Evaluation of Determinants n Geometric Interpretations n Properties of Determinants Reading Assignment: Secs 3. 2, 3. 3, 3. 5 of Textbook Homework #2 due Next Time • Introduction to Eigenvalues n Applications of Determinants n n Vectors in R n Vector Spaces Reading Assignment: Secs 3. 4, 4. 1 -4. 2 2

Lecture 4: Elementary Matrices & Determinants Today n Matrix Computation Packages (Matlab and …) n Evaluation of Determinants n Geometric Interpretations n Properties of Determinants 3

What Did You Actually Learn Last Time? 4

Keywords in Section 2. 4: n row elementary matrix: 列基本矩陣 n row equivalent: 列等價 n lower triangular matrix: 下三角矩陣 n upper triangular matrix: 上三角矩陣 n LU-factorization: LU分解 5

n Thm 3. 1: (Expansion by cofactors) Let A is a square matrix of order n. Then the determinant of A is given by (Cofactor expansion along the i-th row, i=1, 2, …, n ) or (Cofactor expansion along the j-th row, j=1, 2, …, n ) 6

n Ex: The determinant of a matrix of order 3 7

n The determinant of a matrix of order 3: Subtract these three products. Add these three products. 8

n Upper triangular matrix: All the entries below the main diagonal are zeros. n Lower triangular matrix: All the entries below the main diagonal are zeros. n Diagonal matrix: All the entries above and below the main diagonal are zeros. 9

Keywords in Section 3. 1: n determinant : 行列式 n minor : 子行列式 n cofactor : 餘因子 n expansion by cofactors : 餘因子展開 n upper triangular matrix: 上三角矩陣 n lower triangular matrix: 下三角矩陣 n diagonal matrix: 對角矩陣 10

n That is, we’ve got an intuitive justification to interpret det ( as the size of the box formed by the vectors. , . . . , Example The volume of this parallelepiped, which can be found by the usual formula from high school geometry, is 12. 11 )

2 B. 4 Geometry of Determinants: Determinants as Size Functions n We have so far only considered whether or not a determinant is zero, here we shall give a meaning to the value of that determinant. One way to compute the area that it encloses is to draw this rectangle and subtract the area of each subregion. 12

The properties in the definition of determinants make reasonable postulates for a function that measures the size of the region enclosed by the vectors in the matrix. See this case: n The region formed by and is bigger, by a factor of k, than the shaded region enclosed by and. That is, size ( , ) = k · size( , ) and in general we expect of the size measure that size(. . . , , . . . )= k · size(. . . , , . . . ). 13

n n Another property of determinants is that they are unaffected by pivoting Here are before-pivoting and after-pivoting boxes (the scalar used is k = 0. 35). Although the region on the right, the box formed by and , is more slanted than the shaded region, the two have the same base and the same height and hence the same area. This illustrates that 14

n That is, we’ve got an intuitive justification to interpret det ( as the size of the box formed by the vectors. , . . . , Example The volume of this parallelepiped, which can be found by the usual formula from high school geometry, is 12. 15 )

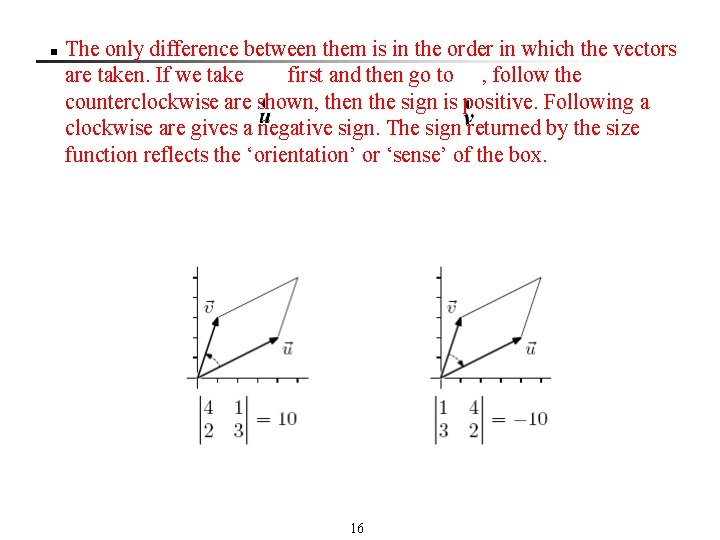
n The only difference between them is in the order in which the vectors are taken. If we take first and then go to , follow the counterclockwise are shown, then the sign is positive. Following a clockwise are gives a negative sign. The sign returned by the size function reflects the ‘orientation’ or ‘sense’ of the box. 16

n Volume, because it is an absolute value, does not depend on the order in which the vectors are given. The volume of the parallelepiped in the following example, can also be computed as the absolute value of this determinant. The definition of volume gives a geometric interpretation to something in the space, boxes made from vectors. 17

Application of the map t represented with respect to the standard bases by will double sizes of boxes, e. g. , from this to 18

3. 2 Evaluation of a determinant using elementary operations n Thm 3. 3: (Elementary row operations and determinants) Let A and B be square matrices. 19

n Ex: 20

Note: A row-echelon form of a square matrix is always upper triangular. Ex 2: (Evaluation a determinant using elementary row operations) n Sol: 21

n Notes: 22

n Notes: 23

n Thm 3. 4: (Conditions that yield a zero determinant) If A is a square matrix and any of the following conditions is true, then det (A) = 0. (a) An entire row (or an entire column) consists of zeros. (b) Two rows (or two columns) are equal. (c) One row (or column) is a multiple of another row (or column). 24

n Ex: 25

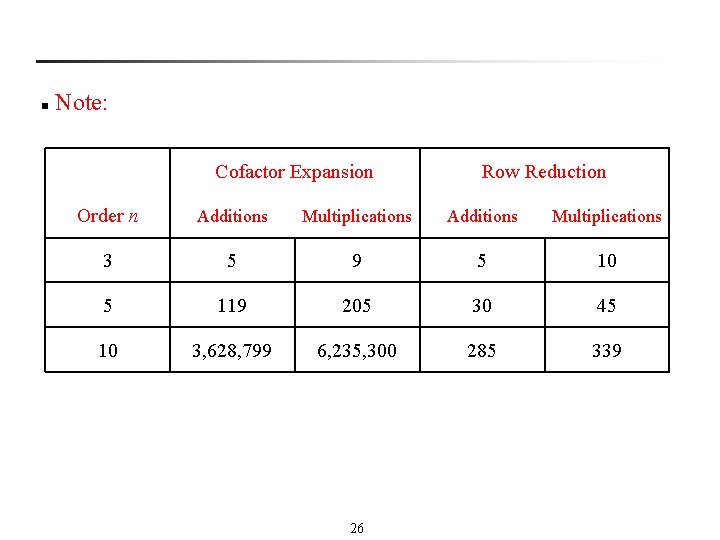
n Note: Cofactor Expansion Row Reduction Order n Additions Multiplications 3 5 9 5 10 5 119 205 30 45 10 3, 628, 799 6, 235, 300 285 339 26

n Ex 5: (Evaluating a determinant) Sol: 27

n Ex 6: (Evaluating a determinant) Sol: 28

29

3. 3 Properties of Determinants n Thm 3. 5: (Determinant of a matrix product) det (AB) = det (A) det (B) n Notes: (1) det (EA) = det (E) det (A) (2) (3) 30

n Ex 1: (The determinant of a matrix product) Find |A|, |B|, and |AB| Sol: 31

n Check: |AB| = |A| |B| 32

Thm 3. 6: (Determinant of a scalar multiple of a matrix) n If A is an n × n matrix and c is a scalar, then det (c. A) = cn det (A) n Ex 2: Sol: Find |A|. 33

n Thm 3. 7: (Determinant of an invertible matrix) A square matrix A is invertible (nonsingular) if and only if det (A) 0 n Ex 3: (Classifying square matrices as singular or nonsingular) Sol: A has no inverse (it is singular). B has inverse (it is nonsingular). 34

n Thm 3. 8: (Determinant of an inverse matrix) n Thm 3. 9: (Determinant of a transpose) n Ex 4: (a) Sol: 35 (b)

n Equivalent conditions for a nonsingular matrix: If A is an n × n matrix, then the following statements are equivalent. (1) A is invertible. (2) Ax = b has a unique solution for every n × 1 matrix b. (3) Ax = 0 has only the trivial solution. (4) A is row-equivalent to In (5) A can be written as the product of elementary matrices. (6) det (A) 0 36

n Ex 5: Which of the following system has a unique solution? (a) (b) 37

Sol: (a) This system does not have a unique solution. (b) This system has a unique solution. 38