Temat Wyraenia wymierne zastosowania 9 i 13 padziernika








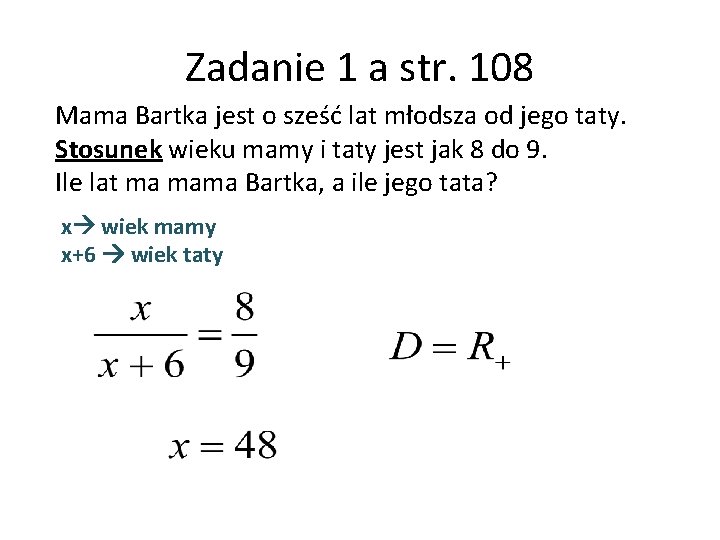

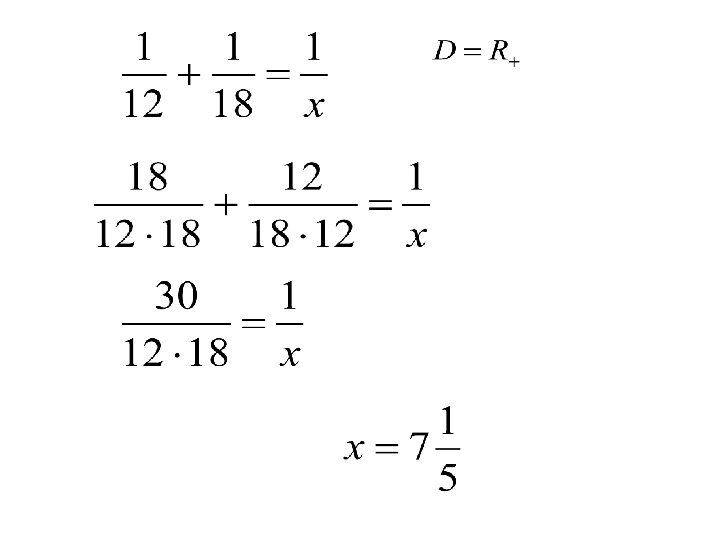

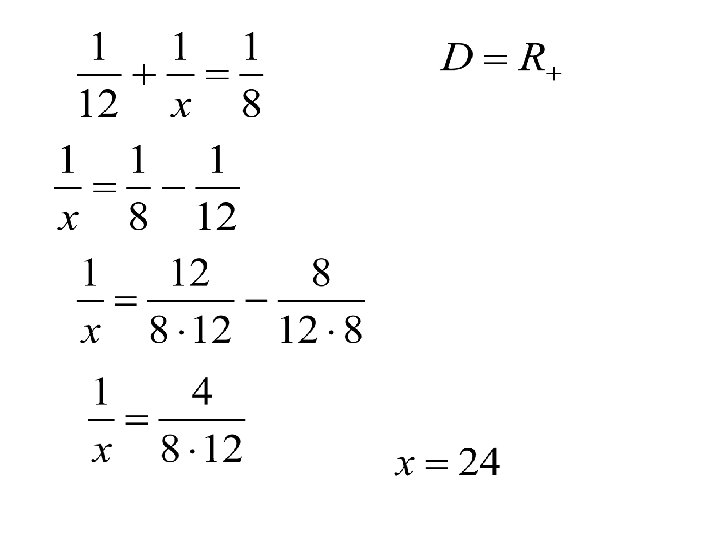

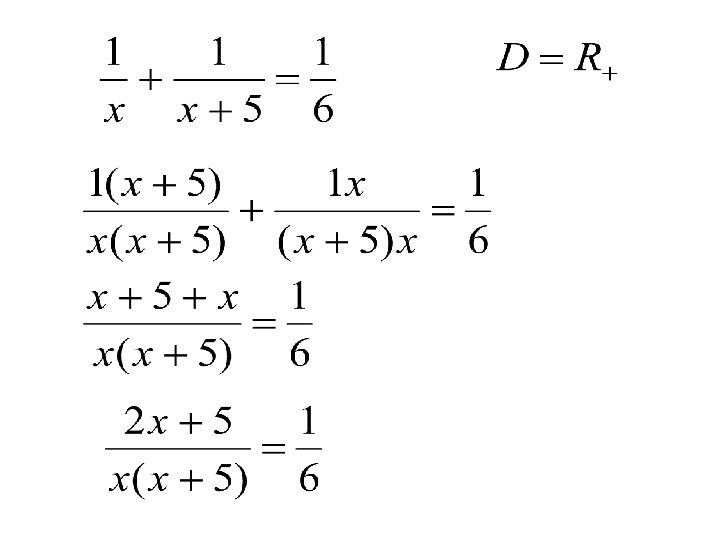













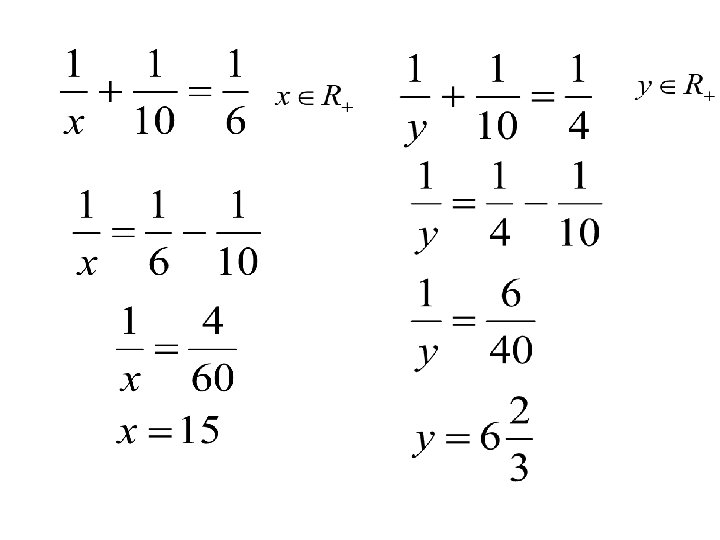
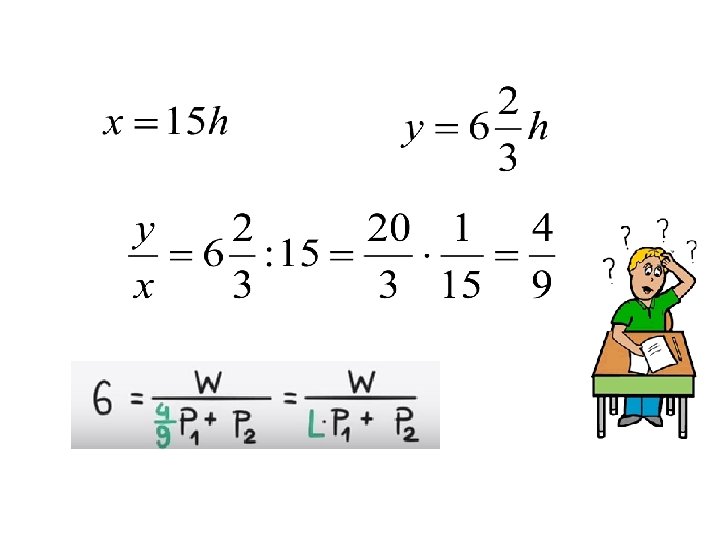







- Slides: 38

Temat: Wyrażenia wymierne - zastosowania 9 i 13 października 2015 3 TIM (2 godziny)

Jak można wykorzystać wiedzę o tym, że dane wielkości są względem siebie odwrotnie proporcjonalne? Czy może to pomóc w rozwiązywaniu zadań?

Cele lekcji: Uczeń: ØPosługuje się wyrażeniami wymiernymi w zagadnieniach osadzonych w kontekście praktycznym ØStosuje przy rozwiązywaniu zadań wyrażenia wymierne w tym proporcjonalność odwrotną ØNabywa umiejętności: wyjaśniania, przekonywania i argumentowania; ØWyrabia wytrwałość i motywację do wysiłku intelektualnego.

Kryteria sukcesu: üPotrafię wykorzystać wyrażenia wymierne do rozwiązywania zadań tekstowych. üPotrafię zapisać analizę zadania (starannie) üPotrafię ułożyć równanie wymierne do zadania osadzonego w kontekście praktycznym.

Zadanie: ćwiczenie- 1 a str. 108 Licznik pewnego ułamka jest równy 10. Jeśli licznik tego ułamka zwiększamy o 20 a mianownik o 30 to wartość ułamka się nie zmieni. Jaki to ułamek?

jeśli D: R{-30, 0} Odp. szukany ułamek to to wartość ułamka nie zmieni się

Zadanie: ćwiczenie- 2 b str. 108 Cena winogron to obecnie x zł/kg. Tydzień temu, kiedy winogrona były o 4 zł za kilogram droższe, Tomek wydał na ich zakup 20 zł. Gdyby obecna cena spadła o 1 zł/kg, to taką samą ilość winogron można by kupić za 12 zł. Jaka jest obecnie cena winogron? Cena 1 kg winogron obecnie x zł Tydzień temu kupił za 20 zł pewną ilość winogrona ale cena była o 4 zł wyższa niż obecnie, czyli (x+4) Obecnie można kupić za 12 zł tę samą ilość winogron ale cena musiała by być o 1 zł niższa niż obecnie, czyli (x-1)

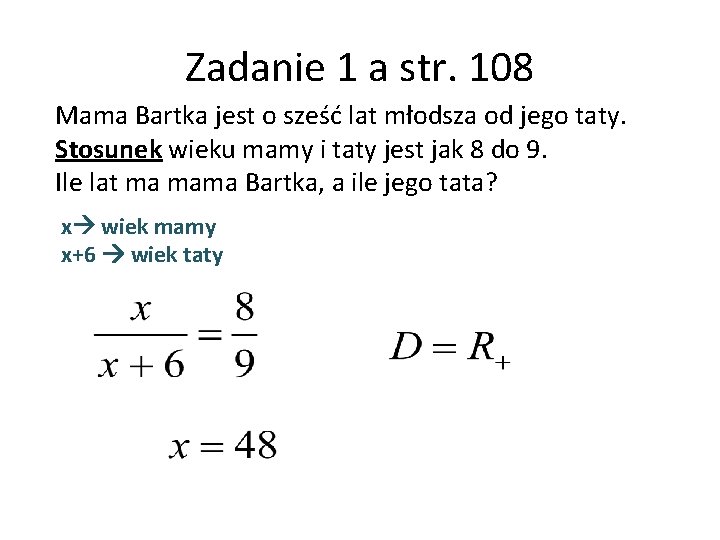
Zadanie 1 a str. 108 Mama Bartka jest o sześć lat młodsza od jego taty. Stosunek wieku mamy i taty jest jak 8 do 9. Ile lat ma mama Bartka, a ile jego tata? x wiek mamy x+6 wiek taty

Zadanie 5 strona 109 Pierwsza koparka wykonała połowę wykopu w ciągu 6 godzin, resztę wykopu wykonała druga koparka w ciągu 9 godzin. Ile czasu zajęłoby wykonanie wykopu, gdyby obie koparki pracowały jednocześnie? X- czas w jakim obie koparki wykonają cały wykop Pierwsza koparka wykonałaby wykop w ciągu 12 godzin, czyli kopała w tempie 1/12 na godzinę Druga koparka wykonałaby wykop w ciągu 18 godzin, czyli kopała w tempie 1/18 na godzinę Gdyby kopały razem to tempo byłoby 1/x na godzinę
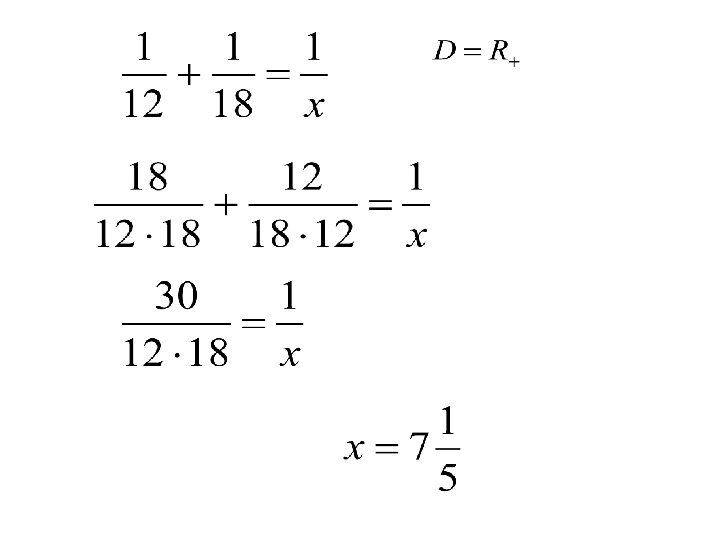

Zadanie 4 strona 109 Dwie koparki, pracując razem wykonują wykop w ciągu 8 dni. Gdyby pracowała tylko pierwsza z nich, wykop powstał by w ciągu 12 dni. Ile czasu zajęłoby wykopanie wykopu drugiej koparce. X- czas w jakim druga koparka wykonałaby cały wykop Pierwsza koparka wykonałaby wykop w ciągu 12 dni, czyli kopała w tempie 1/12 na dzień Dwie koparki wykonały wykop w ciągu 8 dni, czyli kopała w tempie 1/8 na dzień Druga koparka kopała w tempie 1/x na dzień
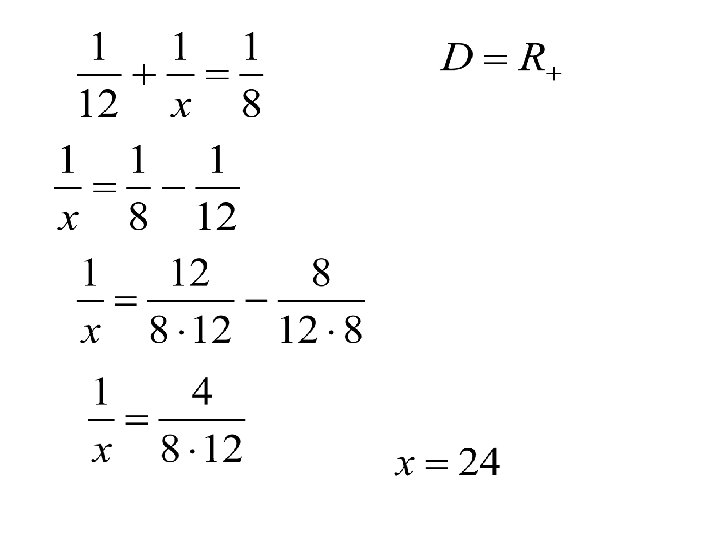

Zadanie ekstra Ojciec i syn zbierają jabłka. Razem zebranie wszystkich jabłek zajęło im 6 godzin. Gdyby ojciec zbierał jabłka sam, to zajęłoby mu to o 5 godzin mniej, niż gdyby zbierał je sam jego syn. W jakim czasie ojciec sam zebrałby wszystkie jabłka? X- czas w jakim ojciec sam zebrałby wszystkie jabłka, a tempo jego pracy to 1/x na godzinę X+5 czas w jakim syn sam zebrałby wszystkie jabłka, a tempo jego pracy to 1/(x+5) na godzinę Razem zbierali w tempie 1/6 na godzinę
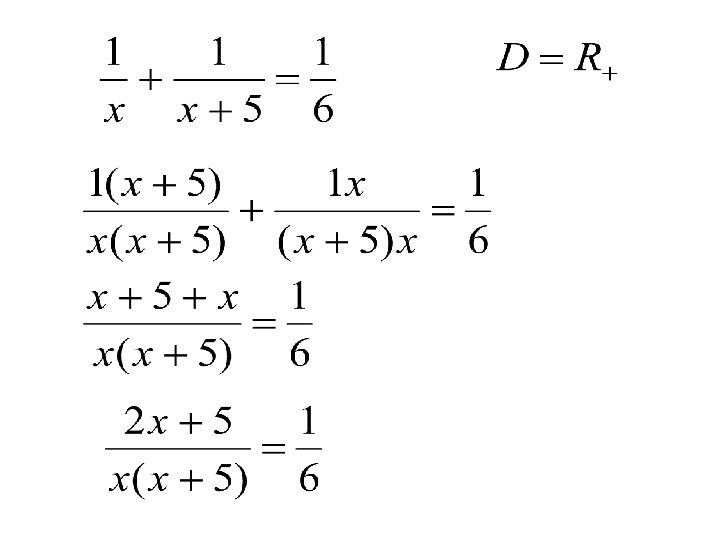

Odp. Ojciec sam zebrałby wszystkie jabłka w ciągu 10 godzin.

Zadanie domowe 1. Licznik pewnego ułamka jest o 6 większy od jego mianownika. Jeśli licznik i mianownik zwiększymy o 11 to otrzymamy ułamek równy 4/3. Znajdź wyjściowy ułamek. b. Licznik pewnego ułamka jest liczbą dodatnią i jest o 3 mniejszy od jego mianownika. Jeśli licznik i mianownik zwiększymy o 10, to otrzymamy ułamek dwa razy większy. Znajdź właściwy ułamek.

Zadanie domowe 2. Licznik pewnego ułamka jest liczbą dodatnią i jest o 3 mniejszy od jego mianownika. Jeśli licznik i mianownik zwiększymy o 10, to otrzymamy ułamek dwa razy większy. Znajdź wyjściowy ułamek.

Zadanie domowe 3. Rodzice Roberta mają na działce truskawki. Zebranie truskawek zajęłoby Robertowi 4 godziny, a jego młodszemu bratu- 6 godzin. Ile czasu zajmie im zbiór truskawek, jeśli będą pracować razem? X- czas w jakim Robert z bratem zbiorą wszystkie truskawki Robertowi zbiór truskawek zająłby 4 godziny, zatem tempo jego zbioru to ¼ części zbioru na godzinę. Bratu zbiór truskawek zająłby 6 godzin zatem tempo jego zbioru to 1/6 części zbioru na godzinę. Gdyby pracowali razem to tempo byłoby 1/x części zbioru na godzinę.

Zadanie domowe 3. Rodzice Roberta mają na działce truskawki. Zebranie truskawek zajęłoby Robertowi 4 godziny, a jego młodszemu bratu- 6 godzin. Ile czasu zajmie im zbiór truskawek, jeśli będą pracować razem?

Wyrażenia wymierne - zastosowania 3 TIM Ciąg dalszy lekcji (13 października)

Zadanie ćwiczenie 1 a str. 110 Samochód jadący ze średnią szybkością v pokonał odległość 195 km. Samochód jadący z szybkością o 20 km/h większą pokonał w tym samym czasie 260 km. oblicz średnie szybkości obu samochodów. s=v·t s − droga t − czas v − szybkość

Oznaczenia i obliczenia

Zadanie ćwiczenie 2 str. 110 Z miast A i B, oddalonych o 510 km, wyruszyły równocześnie naprzeciw siebie dwa pociągi. Średnia szybkość pierwszego była o 10 km/h większa niż szybkość drugiego. Pociągi spotkały się w odległości 270 km od miasta A. Oblicz średnie szybkości, z jakimi poruszały się te pociągi. Analiza: Pierwszy pociąg przejechał: 270 km z szybkością x+10 km/h Drugi pociąg przejechał 240 km z szybkością x km/h Czas trasy pociągów jest wspólny, zakładamy, że pociągi poruszają się ze stałą prędkością.

Oznaczenia i obliczenia

Zadanie 3 str. 111 Trasa rowerowa wokół jeziora ma długość 12 km. Dwóch rowerzystów wyruszyło z tego samego miejsca i okrążało jezioro w tym samym kierunku. Średnia szybkość jednego z nich była o 5 km/h mniejsza niż szybkość drugiego. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora, a wolniejszy 3. Oblicz średnie szybkości obu rowerzystów. s=v·t s − droga, t − czas, v − szybkość

Oznaczenia i obliczenia

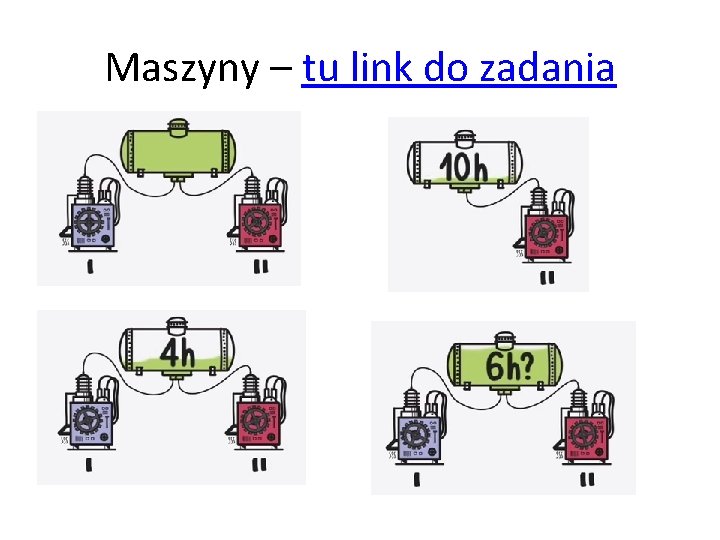
Maszyny – tu link do zadania

X – czas na pracę pierwszej maszyny przed redukcją mocy y– czas na pracę pierwszej maszyny po redukcji mocy 1/10 – moc drugiej maszyny (jest stały) na godzinę 1/6 – moc obu maszyn na godzinę przed redukcją mocy pierwszej 1/4 – moc obu maszyn na godzinę po redukcją mocy pierwszej
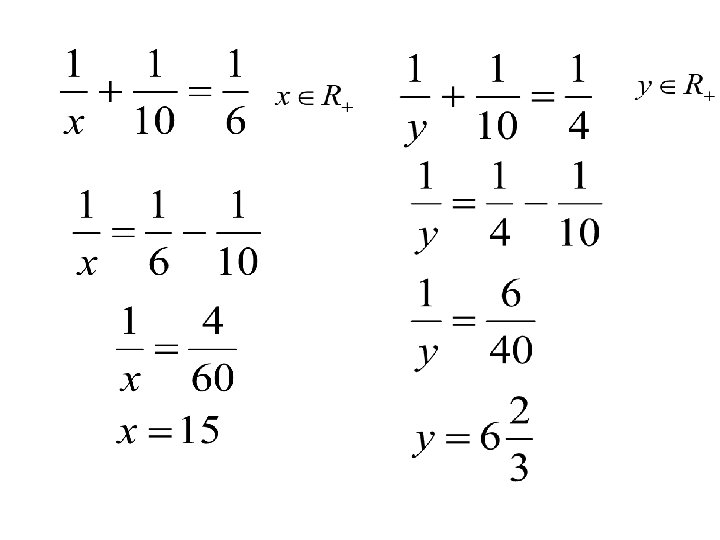
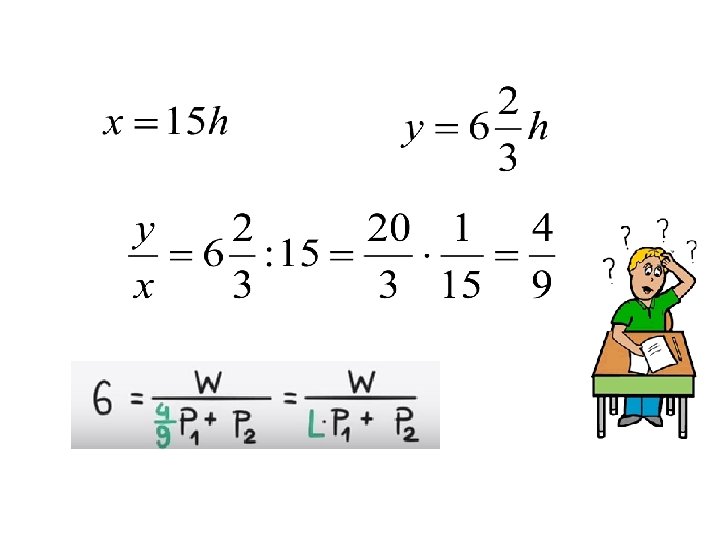

Zadanie Długość pewnej linii kolejowej to około 318 km. Pociąg ekspresowy pokonuje tę trasę o 3 h szybciej niż pociąg osobowy. Szybkość ekspresu jest o 53 km/h większa od szybkości pociągu osobowego. Oblicz średnie szybkości obu pociągów na tej trasie. s=v·t s − droga, t − czas, v − prędkość

Oznaczenia

Obliczenia

Obliczenia

Obliczenia

Obliczenia

Dziękuję za aktywny udział w lekcji Przeanalizuj przed pracą klasową jeszcze raz rozwiązania zadań. Praca klasowa w piątek 16 października