L 3 PRO 1 Echantillonnage Estimation dun paramtre

L 3 PRO 1

Echantillonnage – Estimation d’un paramètre Extraction de n échantillons d’une population P Si l’on extrait plusieurs échantillons représentatifs de taille n fixée, les différences observées entre les résultats obtenus sont dues à des fluctuations d’échantillonnage. A partir d’un échantillon, on n’a donc pas de certitudes mais des estimations de paramètres. L'estimation d'un paramètre peut être faite - par un seul nombre: estimation ponctuelle - par 2 nombres entre lesquels le paramètre peut se trouver: estimation par intervalle 2

Echantillonnage – Estimation d’un paramètre Estimation ponctuelle d’une moyenne x barre Estimateur sans biais Ecart type de la moyenne 3

Echantillonnage – Estimation d’un paramètre Pour améliorer la connaissance de la moyenne, il faut augmenter la taille de l’échantillon 4

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la moyenne Cas des grands échantillons (variance connue): Soit une population obéissant à une loi normale de moyenne m et d’écart type s. 5

Echantillonnage – Estimation d’un paramètre Exemple: 45 hommes à 95% de confiance 6

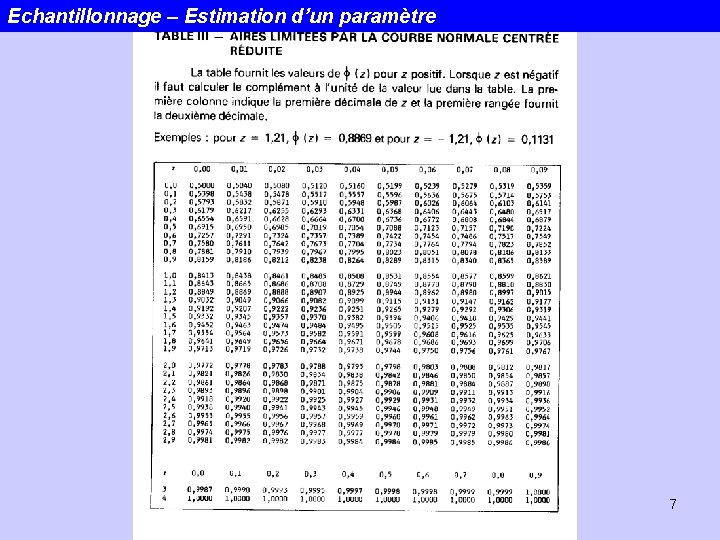
Echantillonnage – Estimation d’un paramètre 7

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la moyenne Cas des petits échantillons: Quand n<30 ou quand la variance est inconnue, on prend la loi de Student. Pour n = n-1 degrés de liberté Finalement on peut toujours utiliser la loi de Student puisque t tend vers la loi normale quand n est grand… 8

La loi de Student: t(n) n degrés de liberté Converge vers la loi Normale quand n augment. 9

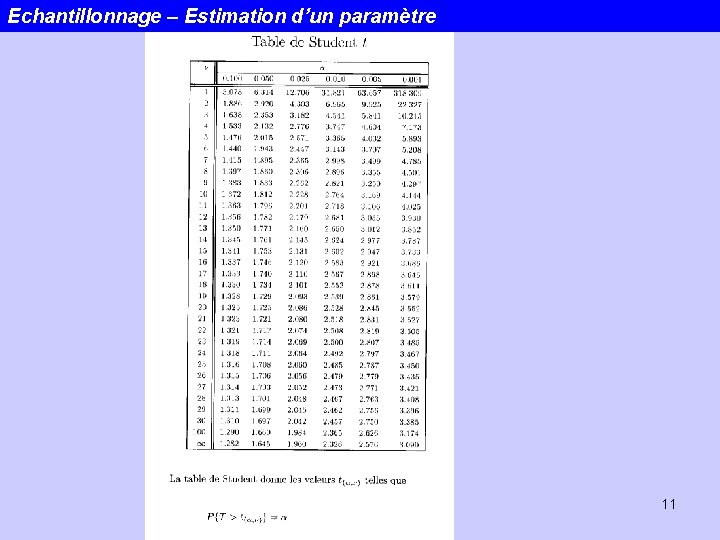
La loi de Student: t(n) La probabilité d’obtenir une valeur de t à l’extérieur de l’intervalle (-ta/2 et ta/2) -> TABLES. 10

Echantillonnage – Estimation d’un paramètre 11

Echantillonnage – Estimation d’un paramètre Exemple: 6 hommes à 95% de confiance Finalement on peut toujours utiliser la loi de Student puisque t tend vers la loi normale quand n est grand… 12

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la variance Soit une population obéissant à une loi normale de moyenne m (inconnue) et d’écart type s (inconnu). Pour n = n-1 degrés de liberté 13

La loi du Khi carré: c 2 Si Z 1, Z 2, Zn sont des variables aléatoires normales centrées réduites et indépendantes entres elles, la somme des carrées de ces varaibles aléatoires obéit à la loi du c 2 à n degrés de libertés 14

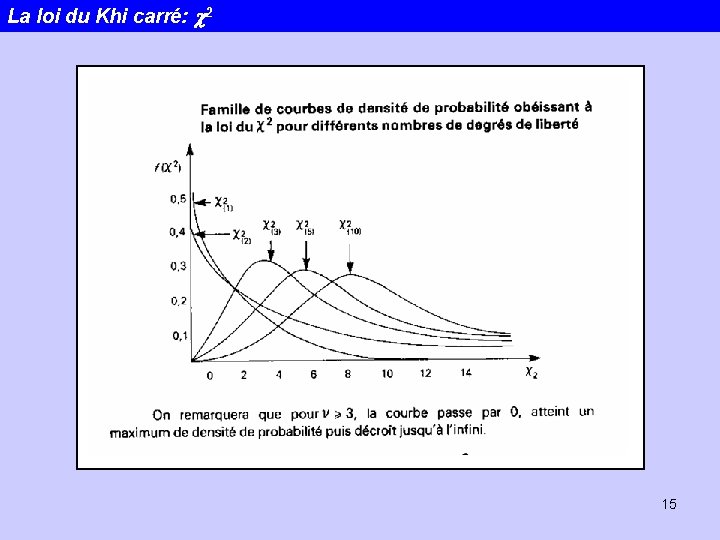
La loi du Khi carré: c 2 15

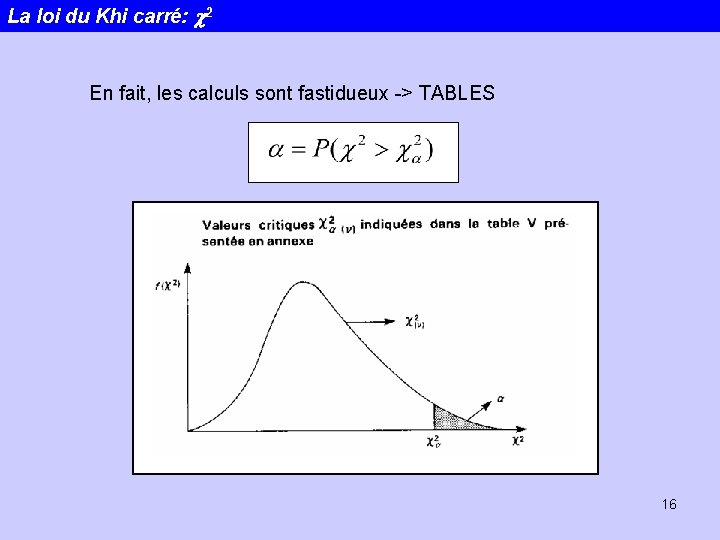
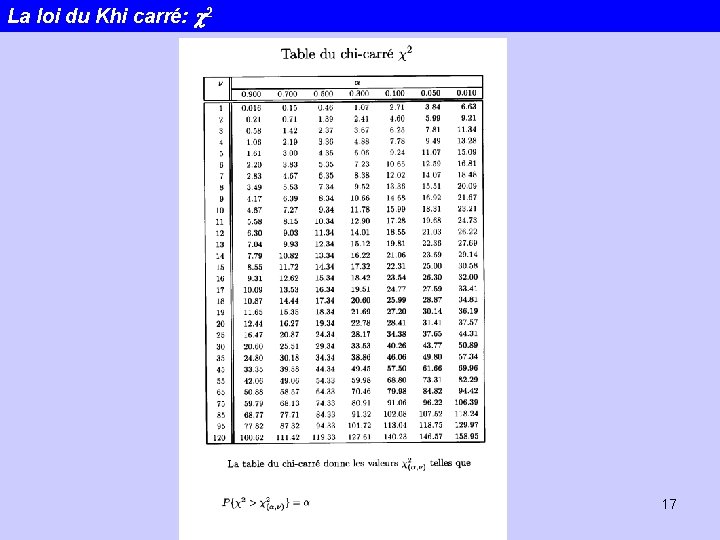
La loi du Khi carré: c 2 En fait, les calculs sont fastidueux -> TABLES 16

La loi du Khi carré: c 2 17

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de l’écart type (idem) Soit une population obéissant à une loi normale de moyenne m et d’écart type s. Pour n = n-1 degrés de liberté 18

Echantillonnage – Estimation d’un paramètre Estimation ponctuelle d’un pourcentage La population est formée d’individus ayant ou non un caractère A. Soit p la probabilité pour qu’un individu pris au hasard dans la population présente le caractère A. Quand on dispose d’un seul échantillon de taille n, la meilleure estimation ponctuelle de P est donc la fréquence p observée sur l’échantillon. 19

Echantillonnage – Estimation d’un paramètre Intervalle de confiance d’un pourcentage Grands échantillons (n>30), p ni voisin de 0, ni voisin de 1, (np>5, n(1 p)>5) La variable fréquence obéit à une loi normale centrée réduite 20

Echantillonnage – Estimation d’un paramètre Un problème très fréquent! Un quotidien publie tous les mois la cote du chef du gouvernement à partir d'un sondage réalisé sur un échantillon représentatif de 1000 personnes. En janvier, la cote publiée était de 38% d'opinions favorables, en février de 36%. Un journaliste commente alors ces valeurs par "Le chef du gouvernement perd 2 points !!" En fait: On construit un intervalle de confiance autour des proportions. Avec un seuil de 95%, on obtient respectivement [35; 41] et [33; 39] pour les valeurs 36% et 38%. Les deux intervalles ayant une intersection non vide, on ne peut pas conclure qu'il y ait eu baisse ou augmentation de la cote du chef de gouvernement. 21

L 3 PRO 22

Théorie de la statistique de décision Quel est le problème…? On sait qu’un homme de néanerthal mesure en moyenne 165 cm. Sur un site on trouve 16 hommes avec une moyenne de 167 et un écart type de 8 cm (e. t. échantillon). Comparaison de la moyenne avec la valeur théorique de 165 cm Possibilités: Moyenne très élevée: Nous pourrons être amenés à croire que ces hommes ont des tailles différentes de 165 cm Moyenne faiblement plus élevée: on ne pourra pas conclure si c’est significativement supérieur à la norme ou si c’est l’effet du hasard. 23

Théorie de la statistique de décision Question: à partir de quelle limite pouvons nous raisonnablement conclure à une différence? H 0: m=165 (il n’y pas de différence) H 1: m≠ 165 Calcul de Sur la table la probabilité pour que la moyenne d’échantillonnage soit différente celle de la population de plus 2, 131 de écart-type est de 5%. 24

Théorie de la statistique de décision Quel est le problème…? On sait qu’un homme de Neandertal mesure en moyenne 165 cm. Sur un site on trouve 40 hommes avec une moyenne de 167 et un écart type de 8 cm (e. t. échantillon). Comparaison de la moyenne avec la valeur théorique de 165 cm Possibilités: Moyenne très élevée: Nous pourrons être amenés à croire que ces hommes ont des tailles différentes de 165 cm Moyenne faiblement plus élevée: on ne pourra pas conclure si c’est significativement supérieur à la norme ou si c’est l’effet du hasard. 25

Théorie de la statistique de décision Question: à partir de quelle limite pouvons nous raisonnablement conclure à une différence? H 0: m=165 (il n’y pas de différence) H 1: m≠ 165 Calcul de On mesure en fait 167 +/- 2. 48 à 95% de confiance, ce qui n’est pas différent de 165 cm! 26

Théorie de la statistique de décision Les deux risques d’erreur dans un test. Erreur de 2 nde espèce (compliquée) 1 -a 1 -b Erreur de 1 ere espèce A priori on ne sait pas à quel type d’erreur on sera confronté: Le résultat de l’échantillon a révélé 167 cm probablement par pur hasard. On conclue que la moyenne pourrait être 165 cm alors qu’en fait elle est mesurée à 167 cm. 27

Théorie de la statistique de décision H 0 : hypothèse nulle ou principale Ex: Les haches de type A présentent les mêmes teneurs en Sn que les haches de type B. H 1 : hypothèse alternative ou contraire … Soumission à une épreuve de vérité! Conclusion : différence attribuable aux fluctuations d’échantillonnage? ? ? 28

Théorie de la statistique de décision Niveau de signification : un peu arbitraire… significatif : 0. 05 hautement significatif : 0. 01 très hautement significatif : 0. 001. Test bilatéral / unilatéral : bilatéral : différence sans se préoccuper du sens. Unilatéral : > ou <. Zone de rejet d’un seul coté de la distribution de probabilité de référence. Echantillons indépendants ou appariés: Indépendants : aucune influence du 1 er ech sur le 2 nd. Appariés : prélèvements par paires. Ex : fumeurs H + F. 29

Comparaison de deux moyennes expérimentales–grands échantillons Comparaison des moyennes de 2 grands échantillons indépendants (n 1 et n 2 >30): Deux échantillons qui suivent des lois normales: m 1, s 21; m 2, s 22 H 0 : m 1 = m 2 Si H 0 est vraie, Zc suit une loi normale N(0, 1) 30

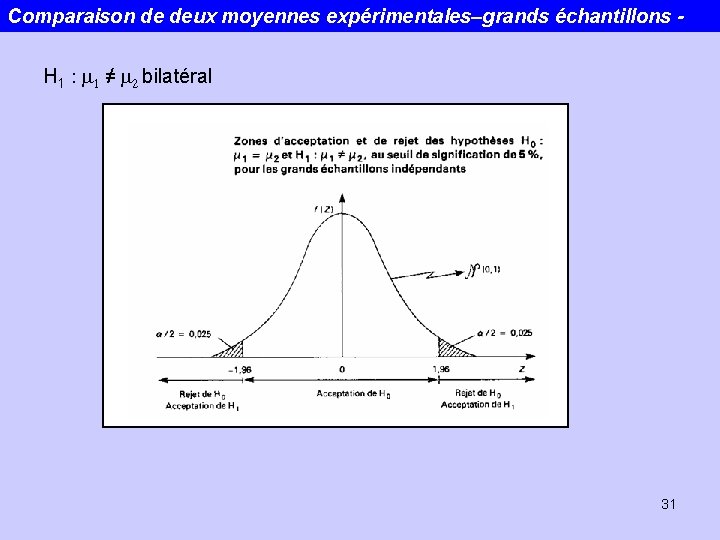
Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 ≠ m 2 bilatéral 31

Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 > m 2 unilatéral 32

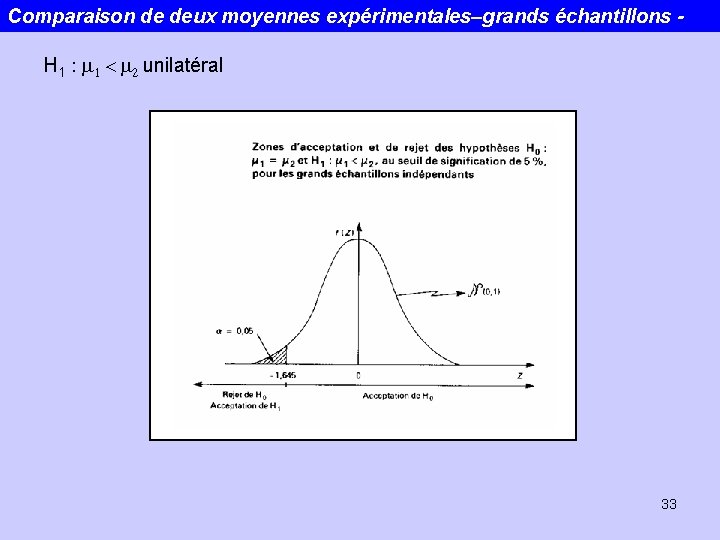
Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 < m 2 unilatéral 33

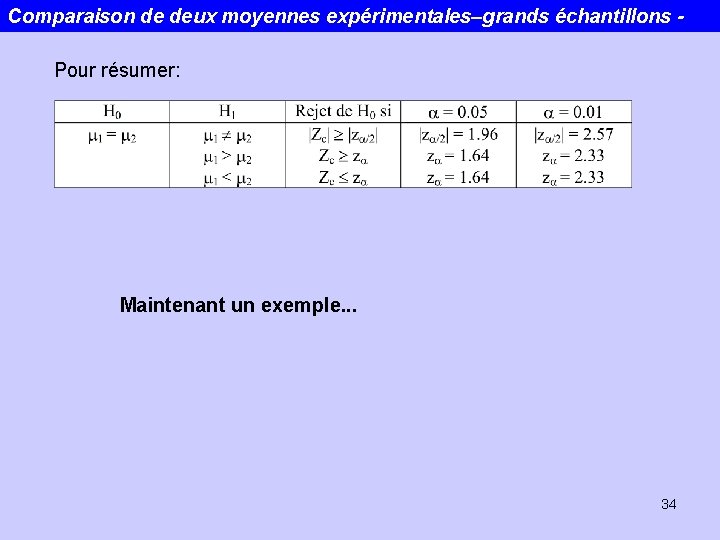
Comparaison de deux moyennes expérimentales–grands échantillons Pour résumer: Maintenant un exemple. . . 34

Comparaison de deux moyennes expérimentales–grands échantillons Taille des silex sur deux sites Les moyennes de ces deux échantillons prélevés indépendamment l’un de l’autre diffèrent-elles d’une façon hautement significative? 35

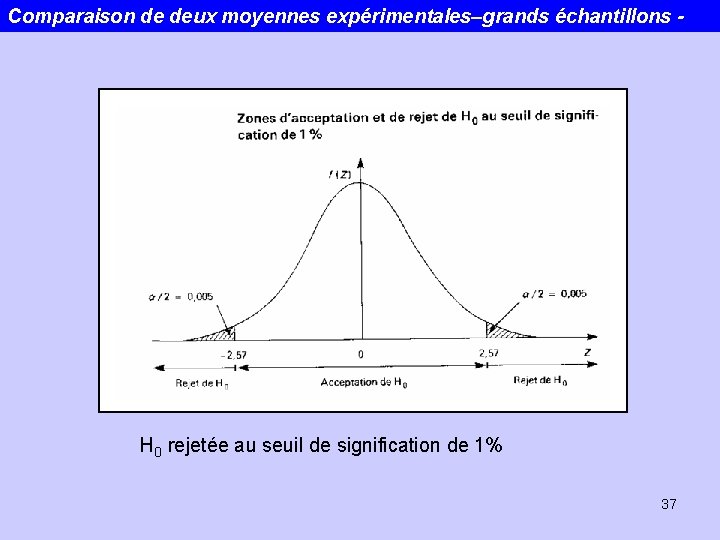
Comparaison de deux moyennes expérimentales–grands échantillons - n 1 et n 2 grands -> test sur la loi normale H 0 : ma = mb H 1 : ma mb (bilatéral) a = 0. 01, Za/2 = 2. 57 36

Comparaison de deux moyennes expérimentales–grands échantillons - H 0 rejetée au seuil de signification de 1% 37

Comparaison d’une moyenne empirique à une moyenne théorique Même principe que précédemment (quand n est grand): H 0: m=m 0 que l’on teste sur la loi normale N(0, 1) 38

Comparaison de deux moyennes expérimentales– petits échantillons Cas des petits échantillons: Test t Deux populations normales m 1 et m 2 de même variance (au moins approximativement) s 2. Si n 1 et n 2 sont petits, s 2 x 1 et s 2 x 2 sont des estimateurs peu précis de s 2. Dans ce cas, la variable différence centrée réduite n’obéit plus à une loi normale mais à une loi de Student à n=n 1+n 2 -2 degrés de liberté. 39

Comparaison de deux moyennes expérimentales– petits échantillons La variance de la distribution des différences de moyennes estimées par s 2 D avec 40

Comparaison de deux moyennes expérimentales– petits échantillons Ce qui donne… H 0 : ma = mb Avec n = n 1 + n 2 - 2 41

Comparaison de deux moyennes expérimentales– petits échantillons Si les variances s’avèrent inégales alors test t modifié. avec 42

Comparaison d’une moyenne empirique à une moyenne théorique Même principe que précédemment. Suivant si n est petit ou grand, on calcule les variables auxiliaires suivantes: H 0: m=m 0 que l’on teste sur la loi de Student ou loi normale N(0, 1) 43

Comparaison de moyennes de deux échantillons appariés Fondée sur les différences de chaque paire d’éléments On imagine que la différence obéit à une loi normale, mais en général on utilise une loi de Student à n-1 degrés de liberté: 44

Comparaison de moyennes de deux échantillons appariés H 0 : m 1 = m 2 ou md = 0 H 1: m 1 m 2 , bilatéral H 1: m 1 > m 2 , unilatéral H 1: m 1 < m 2 , unilatéral t calculé pour n = n-1 degrés de liberté 45

Comparaison de deux fréquences expérimentales Comparaison des fréquences de 2 grands échantillons indépendants. Deux échantillons : f 1, n 1; f 2, n 2 On approxime la loi binomiale par la loi normale mais: n 1>30, n 2>30, n 1 f 1>5, n 2 f 2>5, n 1(1 -f 1)>5, n 2(1 -f 2)>5 H 0 : p 1 = p 2 = p 46

Comparaison de deux fréquences expérimentales Sous H 0 on peut réunir les deux échantillons, et on est conduit à l’estimation de p Zc devient H 1: p 1≠p 2 H 1: p 1>p 2 H 1: p 1<p 2 Test sur la loi normale N(0, 1) 47

Comparaison d’une fréquence empirique et d’une fréquence théorique La différence entre f et p est-elle seulement explicable par les aléas dus à l’échantillonnage? On approxime la loi binomiale par la loi normale mais: n>30, np>5 et nq>5 H 0 : f = p H 1: p 1≠p 2 H 1: p 1>p 2 H 1: p 1<p 2 Test sur la loi normale N(0, 1) 48

Comparaison de deux variances expérimentales Deux échantillons qui suivent des lois normales: m 1, s 21; m 2, s 22 Plus grande variance H 0: s 21=s 22 calcul de : >1 Plus petite variance Si H 0 est vraie, Fc suit une loi de Fisher-Snedecor avec n 1=n 1 -1 et n 2=n 2 -1 49

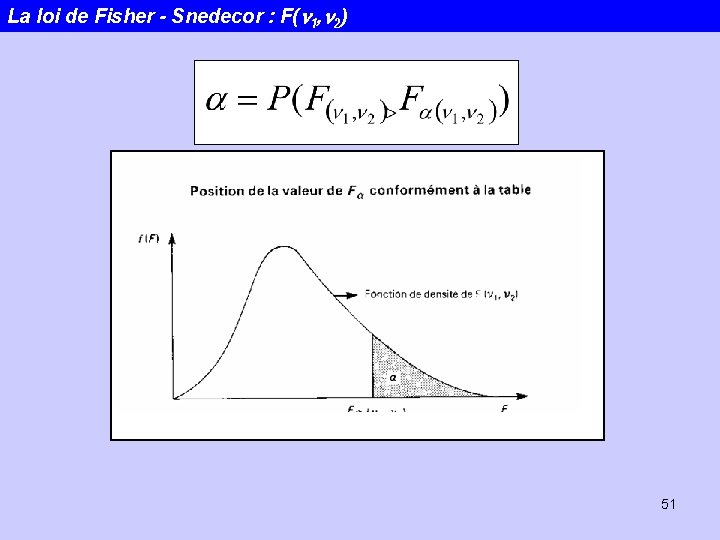
La loi de Fisher - Snedecor : F(n 1, n 2) Soit c 21 et c 22, un couple de variables aléatoires indépendantes suivant respectivement des lois du c 2 à n 1 et n 2 degrés de libertés. Utile pour les tests de variance et de covariance 50

La loi de Fisher - Snedecor : F(n 1, n 2) 51

Comparaison de deux variances expérimentales H 1: s 21>s 22 Sous H 0: Pr(Fc<Fa)=1 -a rejet H 0 Accept. H 0 Fa 52

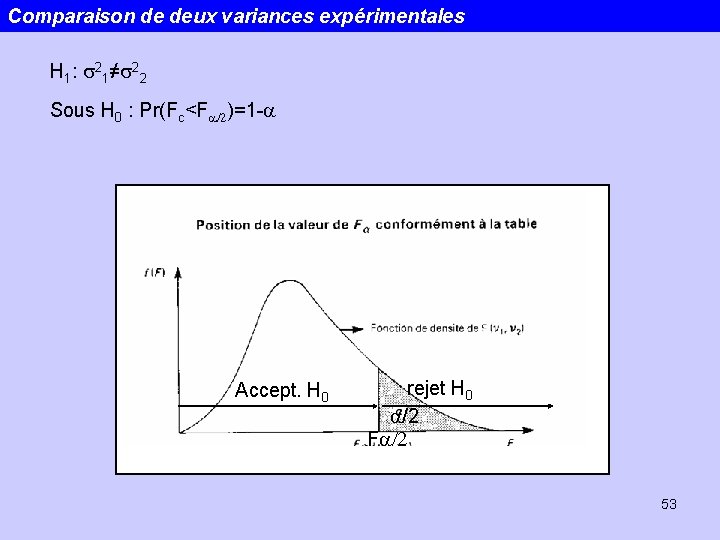
Comparaison de deux variances expérimentales H 1: s 21≠s 22 Sous H 0 : Pr(Fc<Fa/2)=1 -a Accept. H 0 rejet H 0 a/2 Fa/2 53

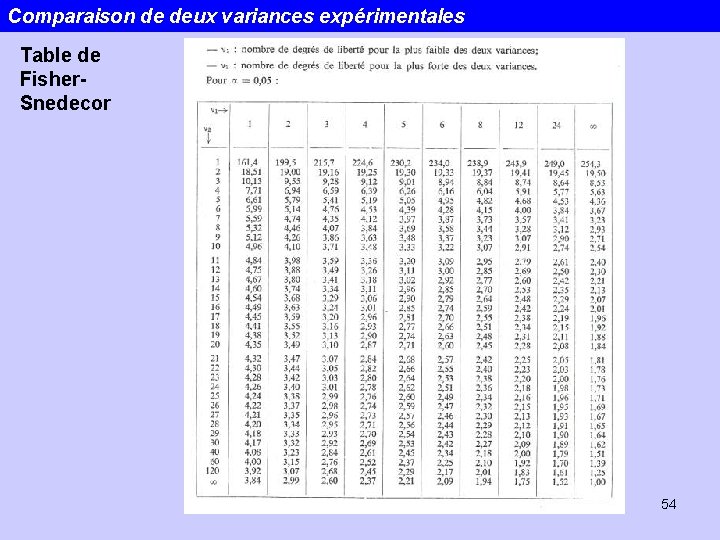
Comparaison de deux variances expérimentales Table de Fisher. Snedecor 54

L 3 PRO 10/19/2021 Statistiques 55

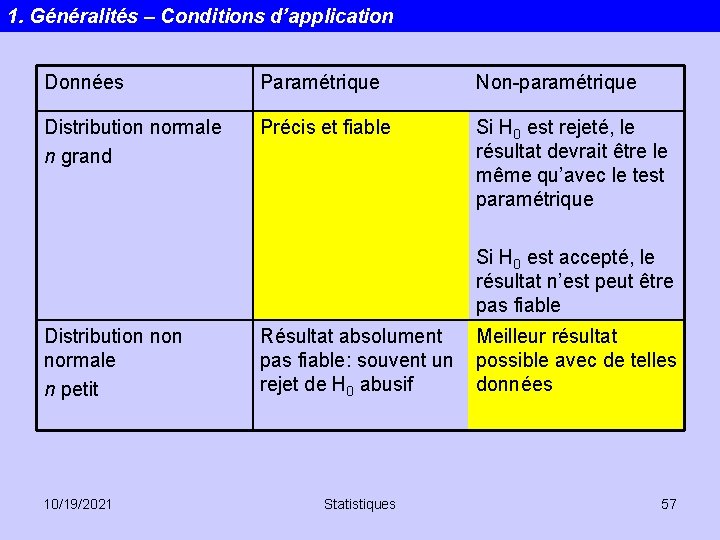
1. Généralités – Conditions d’application Pourquoi et quand utiliser des statistiques non-paramétriques? Les tests non paramétriques ne font aucune hypothèse sur la distribution sousjacente des données. On les qualifie souvent de tests distribution free. L’étape préalable consistant à estimer les paramètres distributions (p. e. moyenne et écart type) avant de procéder au test d’hypothèse proprement dit n’est plus nécessaire. Quand? : 1. L’échelle des données est ordinale plutôt que sous forme d’intervalles ou de rapports. Dans ce cas les opérations arithmétiques n’ont pas de sens! 2. Les mesures sont sur des échelles d’intervalles ou de rapports mais les distributions de fréquences observées sont très éloignées de la distribution normale. 10/19/2021 Statistiques 56

1. Généralités – Conditions d’application Données Paramétrique Non-paramétrique Distribution normale n grand Précis et fiable Si H 0 est rejeté, le résultat devrait être le même qu’avec le test paramétrique Si H 0 est accepté, le résultat n’est peut être pas fiable Distribution normale n petit 10/19/2021 Résultat absolument pas fiable: souvent un rejet de H 0 abusif Statistiques Meilleur résultat possible avec de telles données 57

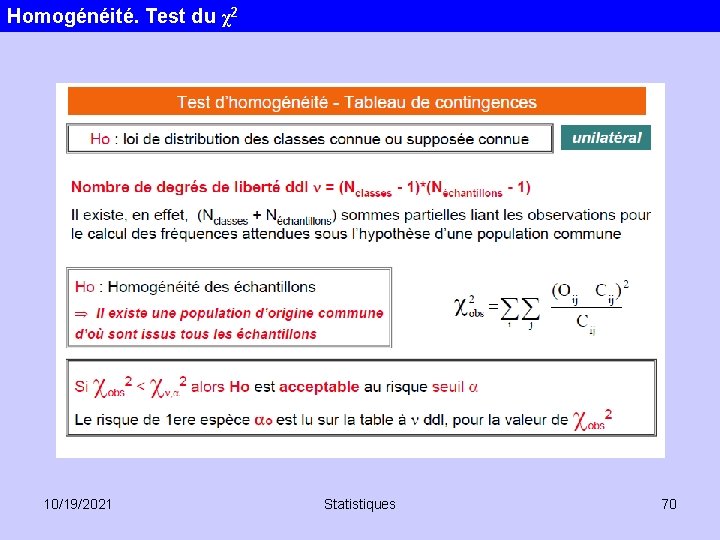
Test du χ2 d’adéquation/conformité: Il s'agit de juger de l'adéquation entre une série de données statistiques et une loi de probabilité définie a priori ou à une population donnée. Test du χ2 d’homogénéité: Il s'agit alors de se demander si deux listes de nombres de même effectif peuvent dériver de la même loi de probabilité. Principe L’analyse se fait à l’aide d’un tableau de corrélation (variables quantitatives regroupées en classes) ou (plus souvent) de contingence (variables qualitatives). Il ne concerne que des données discrètes. On calcule les fréquences attendues de chacune des cases puis les écarts entre celles-ci et les fréquences observées.

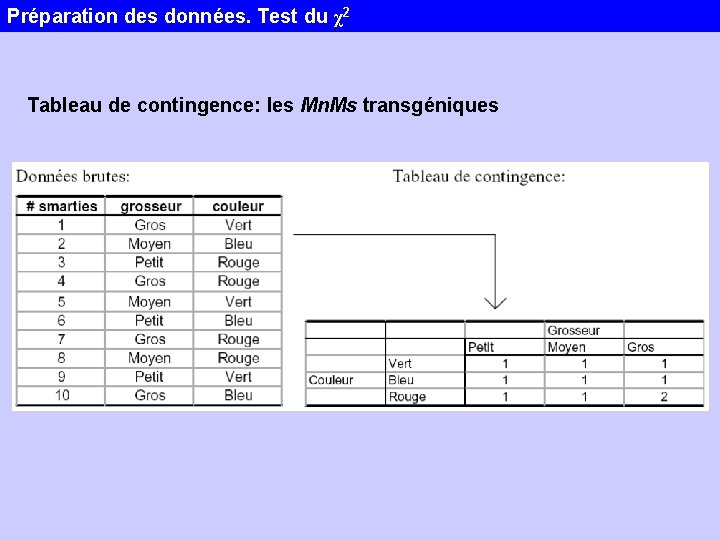
Préparation des données. Test du χ2 Tableau de contingence: les Mn. Ms transgéniques

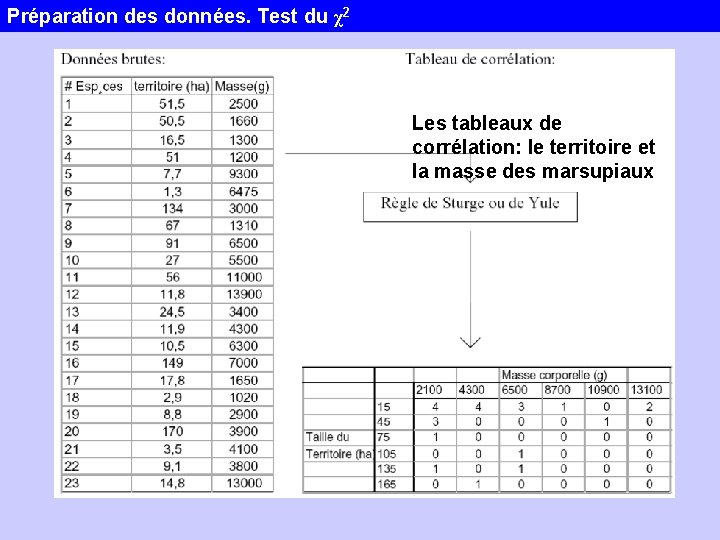
Préparation des données. Test du χ2 Les tableaux de corrélation: le territoire et la masse des marsupiaux

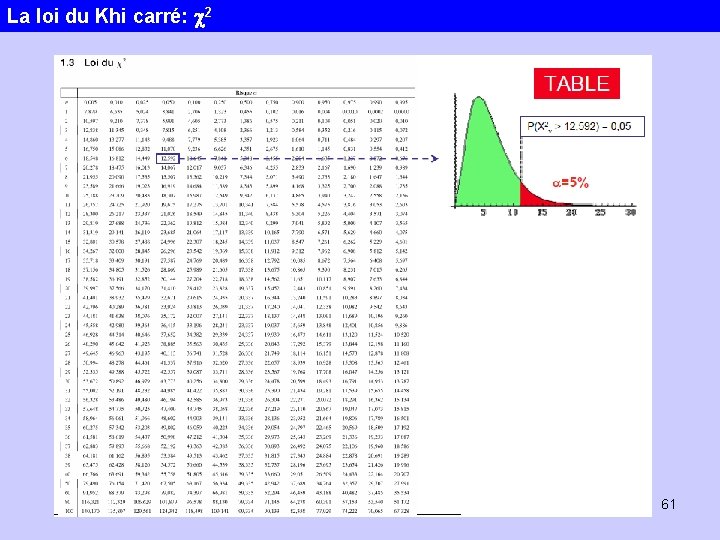
La loi du Khi carré: c 2 61

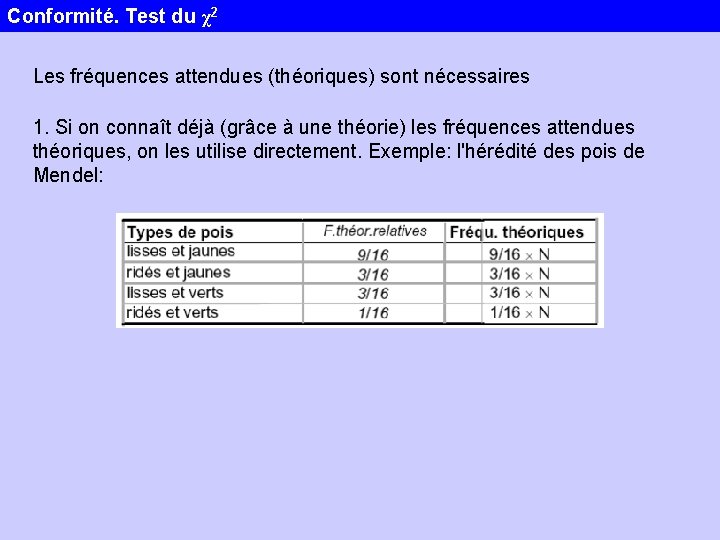
Conformité. Test du χ2 Pour calculer la statistique χ2, on a besoin des: - fréquences absolues observées - fréquences absolues attendues Remarque importante: les fréquences du tableau sont des fréquences absolues observées, jamais des fréquences relatives!

Conformité. Test du χ2 Les fréquences attendues (théoriques) sont nécessaires 1. Si on connaît déjà (grâce à une théorie) les fréquences attendues théoriques, on les utilise directement. Exemple: l'hérédité des pois de Mendel:

Conformité. Test du χ2 H 0 : Il n’y a pas de relation entre les variables… χ2 = 0 H 1: Il y a une relation entre les variables… χ2 > 0

Conformité. Test du χ2 où, si N est la fréquence totale H 0: c 2=0 H 1: c 2>0 Si c 2 = 0, fréq théoriques identiques aux fréq. obs. , si c 2 > 0, elles ne sont pas exactement identiques.

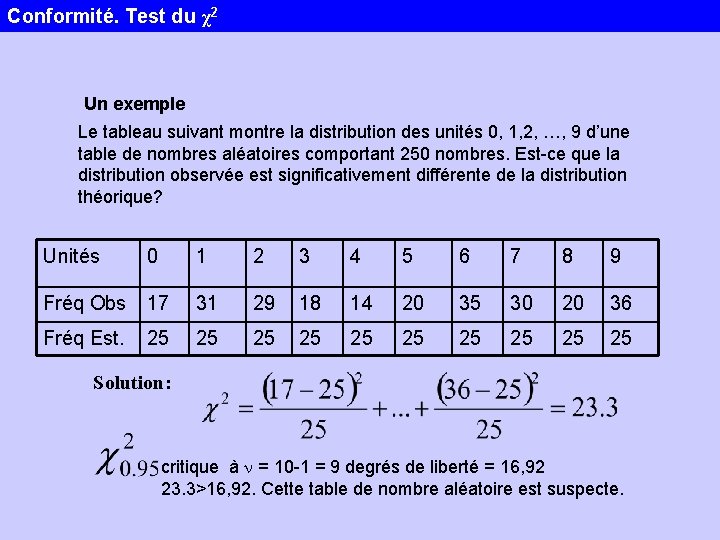
Conformité. Test du χ2 Un exemple Le tableau suivant montre la distribution des unités 0, 1, 2, …, 9 d’une table de nombres aléatoires comportant 250 nombres. Est-ce que la distribution observée est significativement différente de la distribution théorique? Unités 0 1 2 3 4 5 6 7 8 9 Fréq Obs 17 31 29 18 14 20 35 30 20 36 Fréq Est. 25 25 25 Solution: critique à n = 10 -1 = 9 degrés de liberté = 16, 92 23. 3>16, 92. Cette table de nombre aléatoire est suspecte.

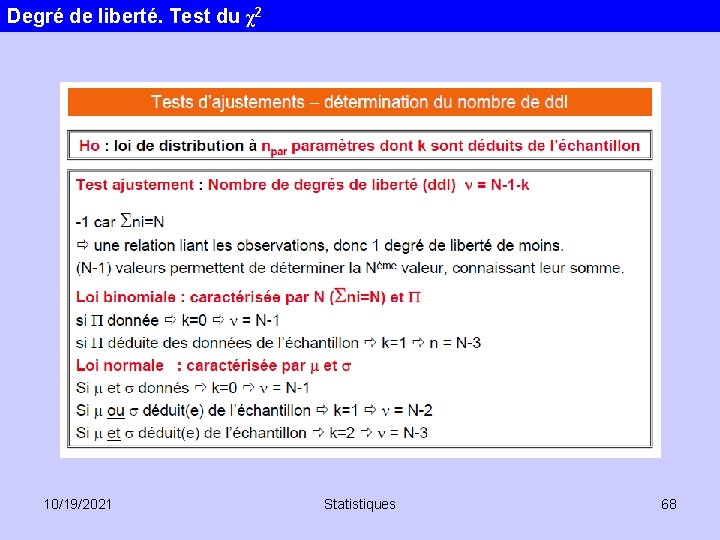
Degré de liberté. Test du χ2 Pourquoi 9 degrés de liberté dans l’exemple précédent? n= k -1 si les fréquences théoriques peuvent être calculées sans avoir à estimer les paramètres de la population à partir des statistiques d’échantillon. n = k – 1 – m si les fréquences théoriques peuvent être calculées en n’estimant que m paramètres de la population à partir des statistiques d’échantillon. Idéalement, au moins 5 occurrences par case!

Degré de liberté. Test du χ2 10/19/2021 Statistiques 68

Homogénéité. Test du χ2 10/19/2021 Statistiques 69

Homogénéité. Test du χ2 10/19/2021 Statistiques 70

Homogénéité. Test du χ2 Guérit Ne guérit pas Total Groupe A (serum) 75 25 100 Groupe B (sans sérum) 65 35 100 Total 140 60 200 Fréquences observées Guérit Ne guérit pas Total Groupe A (serum) 70 30 100 Groupe B (sans sérum) 70 30 100 Total 140 60 200 Fréquences attendues sous H 0 Impossibilité de rejeter H 0

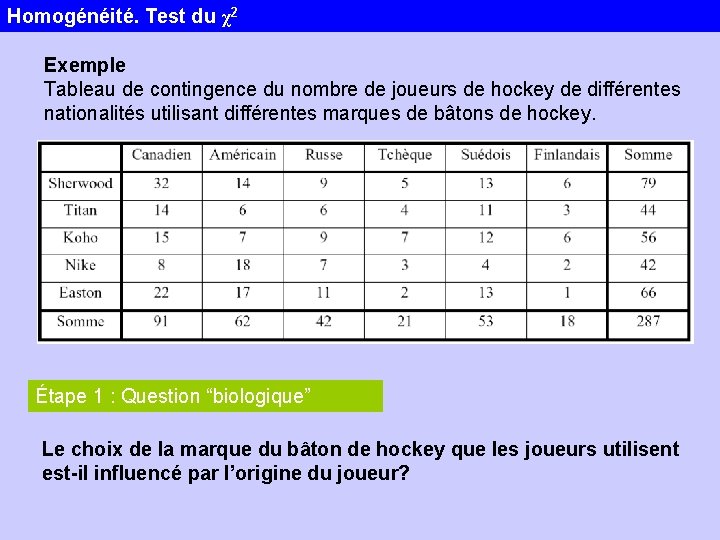
Homogénéité. Test du χ2 Exemple Tableau de contingence du nombre de joueurs de hockey de différentes nationalités utilisant différentes marques de bâtons de hockey. Étape 1 : Question “biologique” Le choix de la marque du bâton de hockey que les joueurs utilisent est-il influencé par l’origine du joueur?

Homogénéité. Test du χ2 Étape 2: Déclaration des hypothèses H 0: il n’y a pas de préférence de marque de bâton de hockey chez les joueurs de différentes nationalités (donc: la variable "marque de bâton" et la variable "nationalité" sont indépendantes) : χ2 = 0 H 1: les joueurs de différentes nationalités ont des préférences différentes au niveau de la marque de bâton de hockey qu’ils utilisent : χ2 > 0 Étape 3 : Test statistique utilisé Étape 4: Conditions d’application • données sous forme de fréquences • indépendance des observations • fréquences distribuées normalement

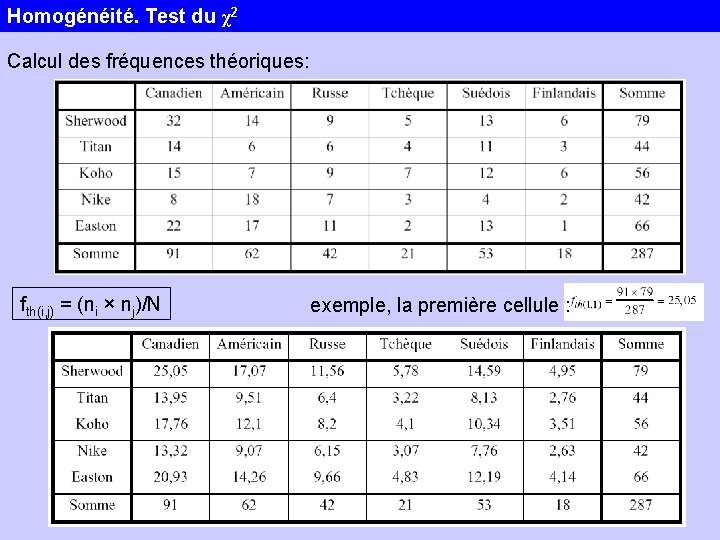
Homogénéité. Test du χ2 Calcul des fréquences théoriques: fth(i, j) = (ni × nj)/N exemple, la première cellule :

Homogénéité. Test du χ2 Étape 5 : Distribution de la variable auxiliaire Si H 0 est vraie, la statistique χ2 calc suit une distribution de χ2 à υ = (l – 1) × (c – 1) = (5 – 1) × (6 – 1) = 20 d. d. l. Étape 6 : Règle de décision On rejette H 0 si χ2 calc ≥ χ2(0, 05, 20) = 31, 41 Étape 7: Calcul du test Étape 8: Décision statistique On ne rejette pas H 0 au seuil α = 0, 05 car si χ2 calc < χ2(0, 05, 20) Étape 9: Interprétation biologique Les joueurs de différentes nationalités n’utilisent pas des bâtons de hockey de marques différentes car les compagnies font la promotion de leurs bâtons avec la même intensité dans les pays étudiés.

1. Généralités – Les tests non paramétriques en pratique 10/19/2021 Statistiques 76