Jak potali ve starm Egypt 2 Mgr Jaromr

Jak počítali ve starém Egyptě 2 Mgr. Jaromír Osčádal

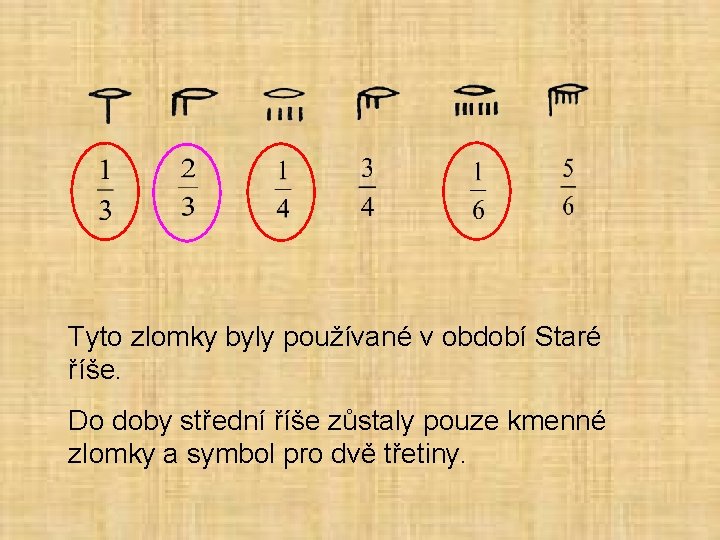
Znali Egypťané zlomky? • Už v archaickém období používali zlomky. • Mezi nejstarší zlomky patří ty, které vznikaly metodou půlení (jedna polovina a čtvrtina, …) • V počátcích kromě kmenných zlomků: používali i doplňkové zlomky:

Tyto zlomky byly používané v období Staré říše. Do doby střední říše zůstaly pouze kmenné zlomky a symbol pro dvě třetiny.

Jak zapisovali zlomky? • Kmenné zlomky psali v hieroglyfickém písmu znakem nad celým číslem jmenovatele. = • V hieratickém písmu zlomek zapisovali tečkou nad číslem. =

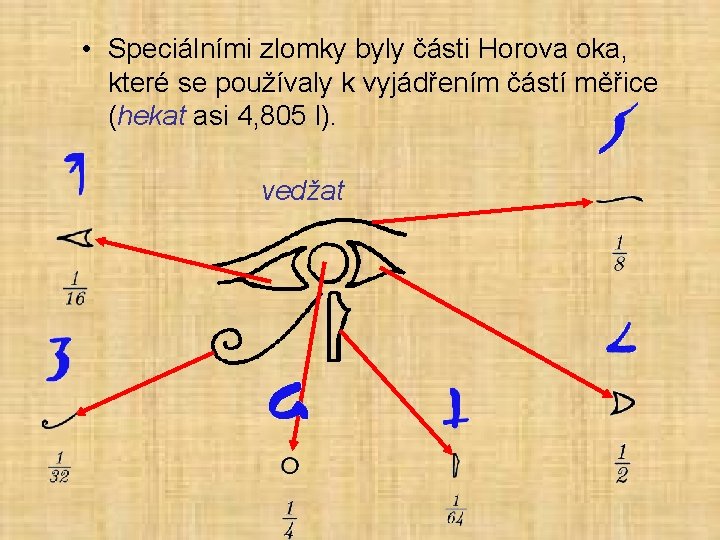
• Speciálními zlomky byly části Horova oka, které se používaly k vyjádřením částí měřice (hekat asi 4, 805 l). vedžat

Jak zapisovali ostatní zlomky? • Ostatní zlomky zapisovali jako konečnou řadu různých kmenných zlomků.

• Čísla větší než jedna zapisovali formou smíšených čísel.

Proč to tak dělali? • Egypťané používali matematiku k praktickým výpočtům. • Chyběla jim obecná představa o racionálních číslech.

Proč to tak dělali? • André Weil označil rozhodnutí zapisovat zlomky formou kmenných zlomků jako „Wrong Turn“. • Ale pro starověké Egypťany to muselo nějakou výhodu mít. • Kmenné zlomky užívali i jiné civilizace.

Z praktického dělení úrody uměli Egypťané rozdělit celek na n dílů, ale představa rozdělit m celků, a každý celek na n dílů, byla pro ně nepraktická.

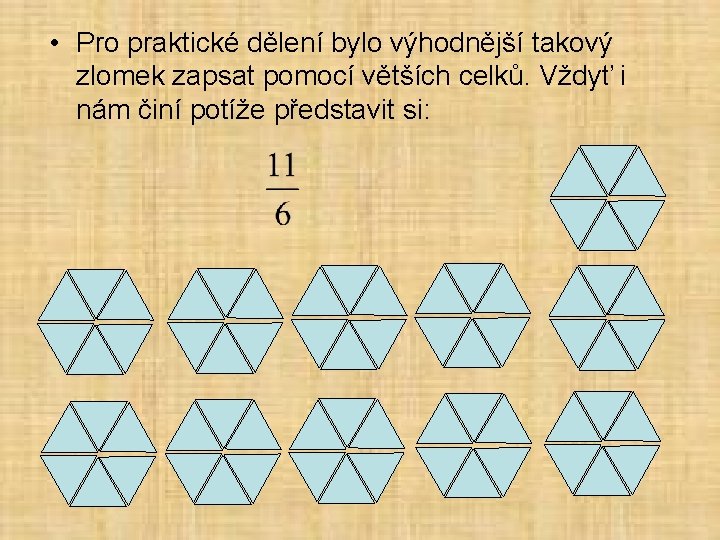
• Pro praktické dělení bylo výhodnější takový zlomek zapsat pomocí větších celků. Vždyť i nám činí potíže představit si:

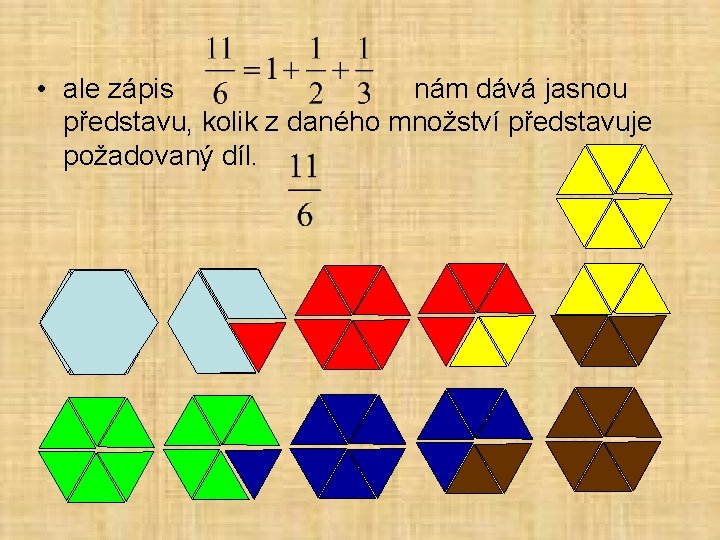
• ale zápis nám dává jasnou představu, kolik z daného množství představuje požadovaný díl.

Úloha na dělení chleba • Rozdělte 5 chlebů mezi 7 kameníků. Najdete i jiná rozdělení?

Jaký největší kmenný zlomek se vejde do daného racionálního čísla?

Vymyslete postup, jak můžeme najít zápis ve formě egyptských zlomků.

• Pokuste se zapsat racionální číslo ve tvaru egyptských zlomků.

Lze každý zlomek 2/n zapsat ve tvaru egyptského zlomku? • Co když je n sudé

• Co když je n liché

• Co když je n liché

Příklady: Vynechání kroku 3/n

Lze zlomek 3/n zapsat ve tvaru egyptského zlomku? • Jak můžeme zapsat n?

• V takovém případě můžeme zlomek zkrátit.

• V takovém případě platí:

• V takovém případě platí:

• V takovém případě platí: Zlomek 2/n lze rozdělit na kmenné zlomky, protože zlomek 1/(k+1) je největší kmenný zlomek , který se vejde do hodnoty 3/n, musí další zlomky být menší (jiné).

Příklady:

Lze každý zlomek m/n zapsat ve tvaru egyptského zlomku? 1/ Pro m = 2 nebo m = 3 jsme rozklad na egyptské zlomky dokázali na předchozích stránkách. 2/ Předpokládejme, že existuje m – 1, pro které všechny zlomky h/n, kde h m - 1 (h, n, m Z), lze vyjádřit ve tvaru egyptských zlomků. 3/ Bude to samé platit pro m ?

• Pro jednoduchost uvažujme zlomky menší než jedna.

Pro z 0 můžeme dokázat, že

Pokud z = 0, lze zlomek krátit na kmenný.

Pokud z 0 je čitatel druhého zlomku rozkladu menší než m. Podle předpokladu lze takový zlomek vyjádřit ve tvaru egyptských zlomků, které jsou menší (jiné) než Všechny zlomky n/m menší než jedna, lze zapsat ve tvaru egyptských zlomků (konečného počtu kmenných zlomků).

Existuje jediný zápis zlomku ve tvaru egyptského zlomku? • Tento postup poprvé publikoval v roce 1202 Leonardo z Pisy známý jako Fibonacci. • My jsme si ukázali jen jeden postup, ale podobných může existovat více s jiným výsledkem. • Např. nemusíme vždy použít největší kmenný zlomek.

• Zapište zlomek ve tvaru egyptských zlomků.

Zkuste najít různé zápisy zlomků:

• Představme si zlomek, který lze zapsat pouze v jedné podobě. • Seřadíme kmenné zlomky v zápisu od největšího po nejmenší. • Jak můžeme použít následující rovnosti pro získání dalšího zápisu? • To vede ke sporu s předpokladem jediného zápisu.

Rychle zapište další zápis daného zlomku • Využijte rovností:

Jaký bude základní zápis egyptského zlomku? • Ukázali jsme si, že jeden zlomek lze zapsat v několika tvarech. • Můžeme jeden z nich považovat za jakýsi základní tvar? • Může být určující počet kmenných zlomků?

Jaký bude základní zápis egyptského zlomku? • Za základní tvar můžeme považovat výsledek našeho postupu, který se skládá z největších kmenných zlomků. • Tento postup patří do skupiny takzvaných „hladových algoritmů“, protože do zápisu vložíme vždy největší kmenný zlomek, který se vejde do zbylé hodnoty.

Jaký bude základní zápis egyptského zlomku? • Bohužel jen velmi těžko určíme, zda daný zápis pomocí egyptských zlomků je tento základní. • Jednou z možností je zlomky sečíst a přepočítat podle algoritmu. • Je ale výhodný pro porovnávání zlomků.

• Zlomek je zapsán v základním tvaru, pokud součet posledních zlomků s největším zlomkem 1/n je menší než 1/(n-1).

• Zjistěte, zda je daný zápis zlomků v základním tvaru: NE

• Zjistěte, zda je daný zápis zlomků v základním tvaru: ANO

Porovnávání zlomků

• Které číslo je větší? nebo . • Zápis a nám dává jasnou představu, který z daných zlomků je větší. • Tento zápis má pro porovnání zlomků jasnou výhodu.

• Porovnejte zlomky pomocí tvaru egyptských zlomků:

Příklady: • Porovnejte zlomky nezapsané v základním tvaru:

• Porovnejte zlomky:

Jak mohli sčítat zlomky? • Pokud kmenných zlomků nebylo mnoho a byly různé, staří písaři je jen připojili k sobě. • Pokud některé kmenné zlomky z obou sčítanců byly stejné, rozložili je pomocí tabulky 2/n, nebo použili univerzálnější postup.

Jak mohli sčítat zlomky? • Kmenné zlomky při sčítání převedeme na společného jmenovatele. Výsledek opět vyjádříme ve formě egyptského zlomku. • Egypťané mnohdy nepoužili společného jmenovatele, každý kmenný zlomek vyjadřovali jako násobek vybraného zlomku. Tyto násobky nemusely být celočíselné.

• Sečtěte zlomky a výsledky ověřte klasickým sčítáním zlomků.

• Sečtěte zlomky a výsledky ověřte klasickým sčítáním zlomků.

Jak odčítali zlomky? • Odečetli stejné kmenné zlomky a zbytek převedli na společného jmenovatele. • Mnohdy nepoužili společného jmenovatele, každý kmenný zlomek vyjadřovali jako násobek vybraného zlomku. Tyto násobky nemusely být celočíselné.

• Odečtěte zlomky:

• Odečtěte zlomky:

• Úlohy z Rhindova papyru: • R 21: doplňte do 1: • R 22: doplňte do 1:

Násobení zlomku celým číslem • Probíhalo jako běžné násobení. • Vynásobte číslem 3.

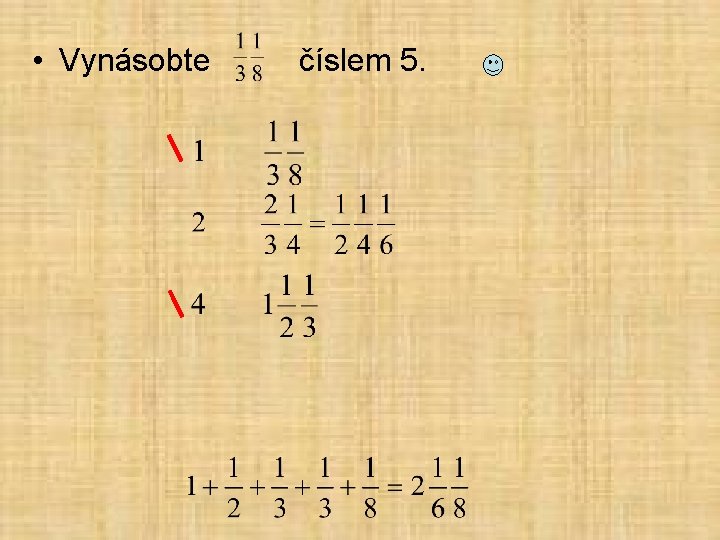
• Vynásobte číslem 5.

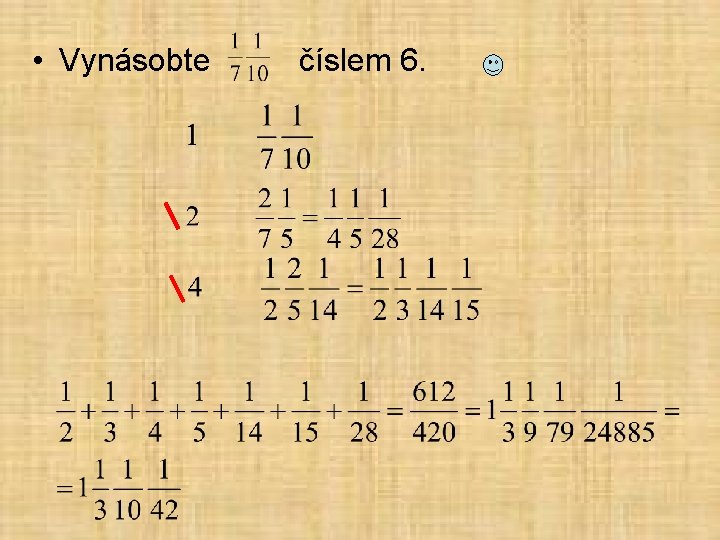
• Vynásobte číslem 6.

Jak násobili zlomky? • Nejvíce příkladů součinu zlomků nalezneme na Rhintově papyru. • Pokud násobíme dva kmenné zlomky, dostaneme opět kmenný zlomek.

Jak násobili zlomky? • Vynásobíme zlomky z obou činitelů, tak jsme zvyklí podle distributivního zákona. • Nakonec sečteme všechny výsledky součinů podle předchozích postupů převodem na společného jmenovatele.

• Vynásobte zlomky:

• Úlohy z Rhindova papyru: • R 7: Vynásobte a : • R 9: Vynásobte a :

Jak písaři dělili zlomky? • V dochovaných úlohách mnoho dělení zlomků nenajdeme. • První skupinou na dělení smíšeným číslem jsou úlohy o kvalitě chleba a piva. • Výsledek se hledal ve formě násobků dělitele, ale v papyrech mnohdy detailní postup chybí.

Rhindův papyrus úloha R 69 • měřice mouky převeďte na 80 chlebů. • Udejte jejich kvalitu. Počítejte s , až najdete 80.

• Udejte jejich kvalitu. Počítejte s , až najdeš 80. • „Vypočítejte, kolik chlebů uděláte z jedné měřice. “

• Výsledek je : Z jedné měřice mouky vyrobíme chlebů.

Egypťané ke každé slovní úloze psali zkoušku L P

Příklad na dělení ve slovní úloze: • R 34: Množství, jehož k němu přidané dají 10.

R 34: Množství, jehož k němu přidané dají 10. 1 7 2 4 7 28 • Čtyřnásobek a dvojnásobek dají víc jak deset, proto vybereme čtyřnásobek a jednonásobek.

• • Do deseti chybí . Vybrané násobky představují . Jednonásobek představuje . Jedna čtvrtina je tedy dělitele. 1 1 4 Výsledek je:

Příklad na dělení ve slovní úloze: • R 32: Množství, jehož k němu přidané dají 2.

• R 32: Množství, jehož k němu přidané dají 2. Výsledek:

Napište zkoušku k této úloze L P

Dělení dvou zlomků je velmi nepohodlné • Vydělte číslem .

• Egypťané znali mnohem víc. Uměli proměřit plochy kruhu, trojúhelníku, lichoběžníku, vypočítat objem válce, hranolu i jehlanu (pyramidy), komolého jehlanu (nedokončené pyramidy), určit sklon pyramidy, využívali podobnosti objektů, počítali členy geometrické a aritmetické posloupnosti, rozdělovali příděly na nestejné díly. Znali mnohem víc!! • MATEMATIKU POTŘEBOVALI KAŽDÝ DEN ŽIVOTA VE STAROVĚKÉM EGYPTĚ.

Binární algoritmus

Představte si zápis racionálního čísla v dvojkové soustavě Tento zápis představuje součet kmenných zlomků. Zápis může být i periodický, i periodu můžeme zapsat ve tvaru kmenných zlomků.

Podobným postupem lze vyjádřit každý periodický zápis pomocí kmenných zlomků typu:

Pomocí zápisu v dvojkové soustavě zapište zlomek ve formě kmenných zlomků

• Podobný postup můžeme uplatnit i pro zápis v trojkové soustavě, kde využijeme rovnosti: • Zápis rozdělíme na řády zapsané jedničkou a řády zapsané dvojkou.

Konec

Použité zdroje: 1) 2) 3) 4) 5) BEČVÁŘ, Jindřich, Martina BEČVÁŘOVÁ a Hana VYMAZALOVÁ. Matematika ve starověku: Egypt a Mezopotámie. 1. vyd. Praha: Prometheus, 2003, 371 s. Dějiny matematiky (Prometheus), sv. 23. ISBN 80 -719 -6255 -4. VYMAZALOVÁ, Hana. Staroegyptská matematika: hieratické matematické texty. Vyd. 1. Praha: Český egyptologický ústav, 2006, 155 s. Dějiny matematiky (Český egyptologický ústav), sv. 31. ISBN 80 -7308156 -3. VYMAZALOVÁ, Hana. Počty v zemi faraonů: matematika stavitelů pyramid. Praha: Český egyptologický ústav Filozofické fakulty Univerzity Karlovy v Praze, 2008, 32 s. ISBN 978 -80 -7363 -215 -1. VYMAZALOVÁ, Hana a Filip COPPENS. Moudrost svitků boha Thovta: vědecké poznání za vlády faraonů. Vyd. 1. Praha: Univerzita Karlova v Praze, Filozofická fakulta, 2011, 352 s. ISBN 978 -807 -3083588. JOHNSON, Paul. Civilizace starého Egypta. Vyd. 1. Praha: Academia, 2002, 262 s. ISBN 80 -200 -0949 -3.

Obrázky • Snímek 1 – http: //en. wikipedia. org/wiki/File: Thoth. svghttp: //cs. wikipedia. org/wiki/Soubor: Thot h. svg – http: //nd 01. jxs. cz/197/156/8237 c 60 d 3 f_23536666_o 2. jpg • Snímek 3 – Zdroj 1) strana 43 • Snímek 4 – Zdroj 1) strana 43 • Snímek 5 – http: //www. aloha. net/~hawmtn/h_eye. gif • Snímek 13 – Zdroj 2) strana 52 • Snímek 82 – http: //en. wikipedia. org/wiki/File: Thoth. svghttp: //cs. wikipedia. org/wiki/Soubor: Thot h. svg