INAOE CURSO PROPEDEUTICO PARA LA MAESTRIA EN ELECTRONICA

INAOE CURSO PROPEDEUTICO PARA LA MAESTRIA EN ELECTRONICA 2010 Métodos Matemáticos Capítulo 2

EDO de segundo orden Métodos Matemáticos - INAOE

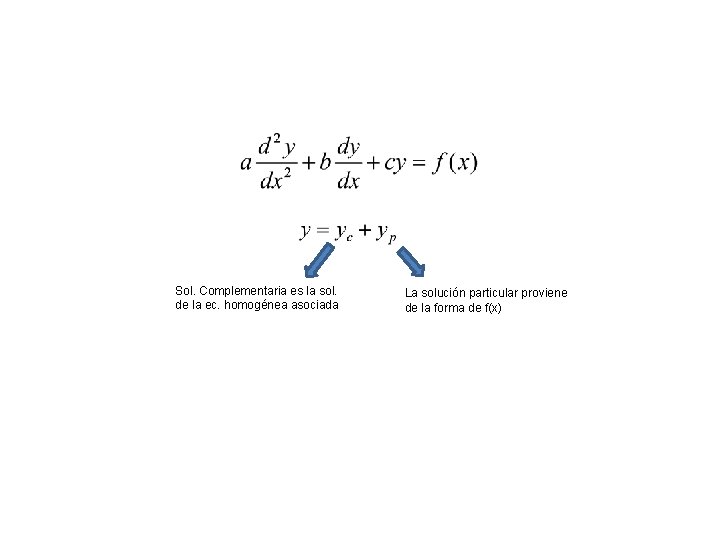
Ecuación Diferencial Ordinaria Lineal de 2 o. Orden Forma General

Sol. Complementaria es la sol. de la ec. homogénea asociada La solución particular proviene de la forma de f(x)

Ecuaciones Homogeneas Ecuación diferencial de segundo orden, lineal, de coeficientes constantes, homogénea Ecuación característica 3 casos: Raíces reales y diferentes Raíces reales e inguales Raíces complejo conjugadas

1 er. Caso: ecuación auxiliar con Raices reales y diferentes.

2 o. Caso: ecuación auxiliar con Raices reales e iguales ecuación auxiliar: Con solución: donde:

3 er. Caso: ecuación auxiliar con Raices complejo conjugadas ecuación auxiliar: Con solución:

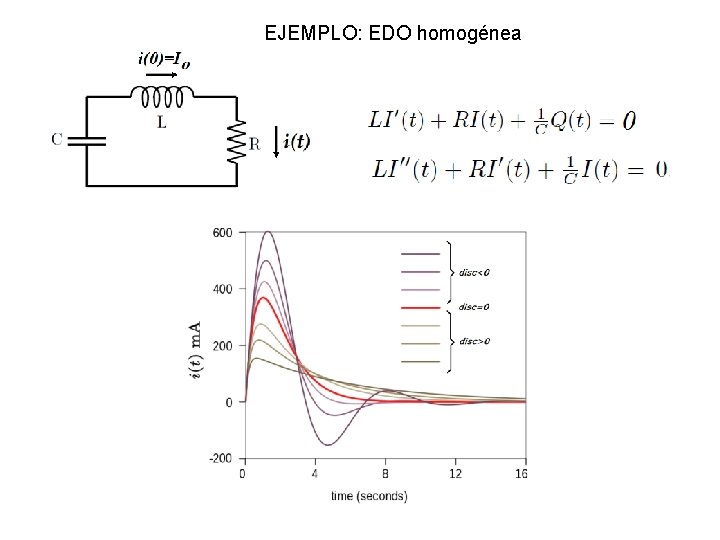
EJEMPLO: EDO homogénea

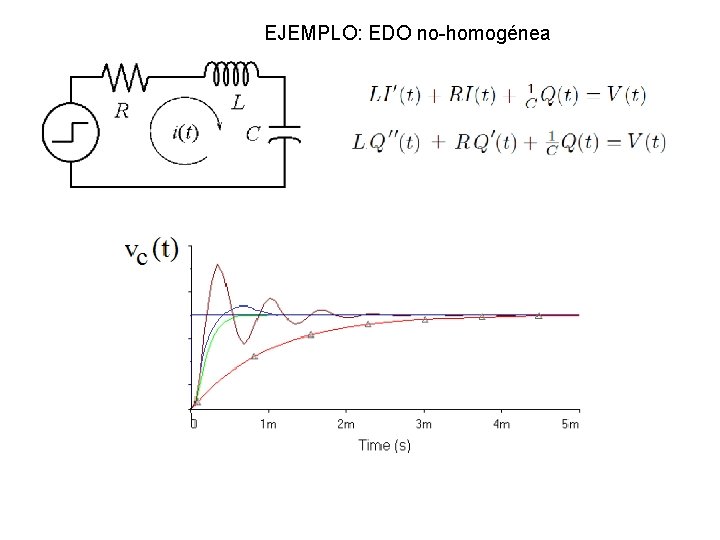
EJEMPLO: EDO no-homogénea

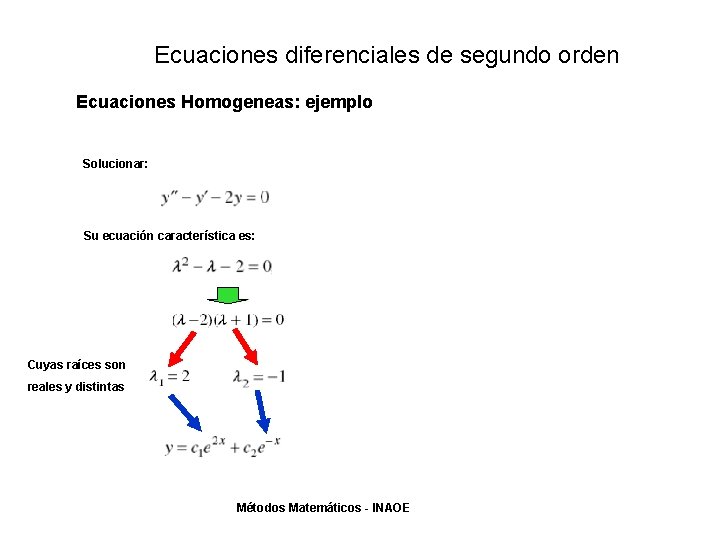
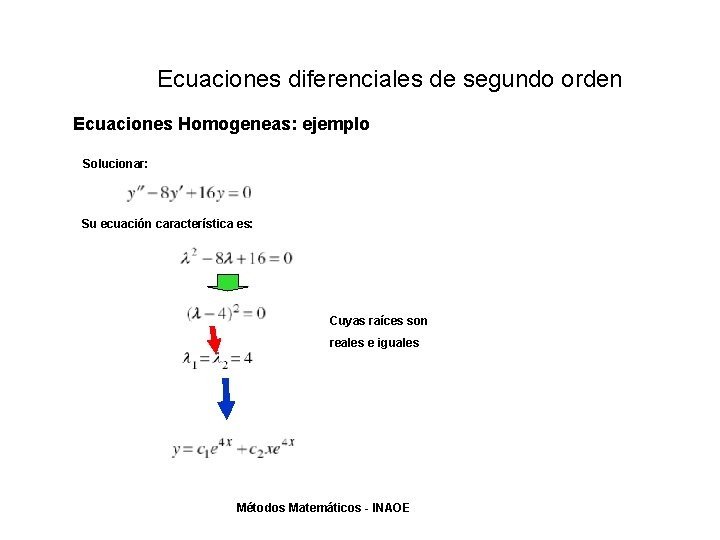
Ecuaciones diferenciales de segundo orden Ecuaciones Homogeneas: ejemplo Solucionar: Su ecuación característica es: Cuyas raíces son reales y distintas Métodos Matemáticos - INAOE

Ecuaciones diferenciales de segundo orden Ecuaciones Homogeneas: ejemplo Solucionar: Su ecuación característica es: Cuyas raíces son reales e iguales Métodos Matemáticos - INAOE

Ecuaciones diferenciales de segundo orden Ecuaciones No-homogeneas. Coeficientes indeterminados La ecuación diferencial de segundo orden, de coeficientes constantes, lineal, no homogénea, es del tipo: La solución está dada en dos partes y 1 + y 2: (a) La parte 1, y 1 es la solución a la ecuaciòn homogénea, y es llamada la solución complementaria. (b) La parte 2, y 2 la cual es llamada la solución particular.

Ecuaciones diferenciales de segundo orden Ecuaciones No-homogeneas: Solución complementaria Ejemplo. Resolver: (a) solución complementaria Ecuación auxiliar: m 2 – 5 m + 6 = 0 la solución m = 2, 3 Y la solución complementaria es y 1 = Ae 2 x + Be 3 x , donde: Métodos Matemáticos - INAOE

…Solución Particular : (b) Solución Particular Se presupone una forma para y 2 tal que y 2 = Cx 2 + Dx + E, y se sustituye en: Lo cual da: Métodos Matemáticos - INAOE

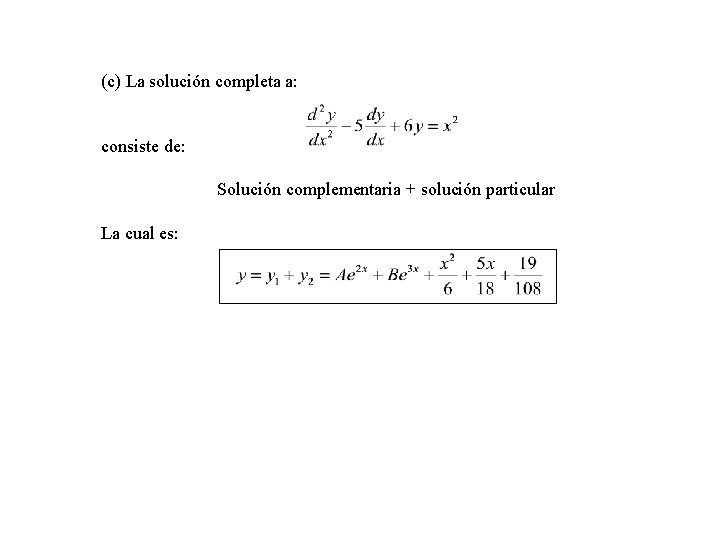
(c) La solución completa a: consiste de: Solución complementaria + solución particular La cual es:

COEFICIENTES INDETERMINADOS Ecuaciones No-homogeneas: Solución Particulares La forma general que se presupone para la integral particular depende de la forma del lado izquierdo de la ecuación no homogénea. La tabla siguiente puede ser usada como una guía:

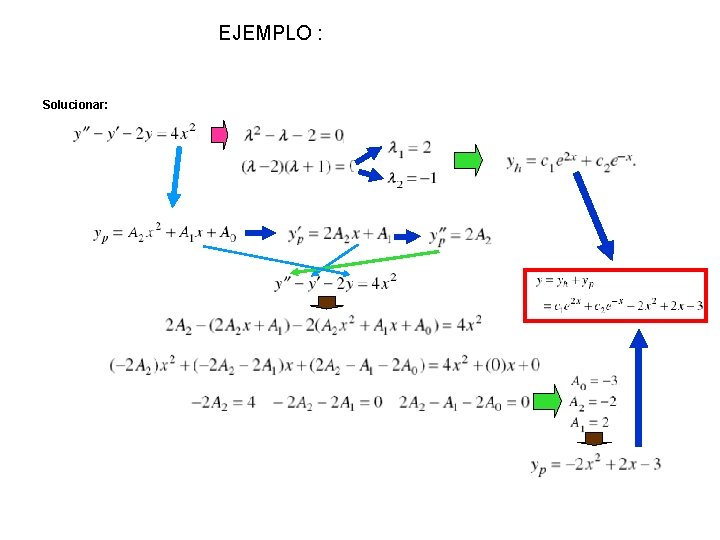
EJEMPLO : Solucionar:

Ejemplo: Solucionar:

EJEMPLO: Resolver la sig. Ec. Dif. no-homogénea de coef. constantes : Ec. Homogénea asociada: Se propone sol. particular: Derivando dos veces: Polinomio característico: Substituyendo en la ec. original y resolviendo para las constantes ABC: Por ecuación de Euler:

ECS. DIF. LINEALES DE ORDEN SUPERIOR : Homogénea:

Ejemplo: Polinomio característico: Sacando raíces: Solución:

Cada par de raíces complejo conjugadas DIFERENTES : Genera un par de funciones linealmente independientes:

Ejemplo: Resolver por variación de parámetros la sig. ec.