INAOE CURSO PROPEDEUTICO PARA LA MAESTRIA EN ELECTRONICA

INAOE CURSO PROPEDEUTICO PARA LA MAESTRIA EN ELECTRONICA 2010 Métodos Matemáticos Capítulo 2

EDO de primer orden Métodos Matemáticos - INAOE

Ejemplo: Ecuaciones diferenciales de primer orden separables

Ecuaciones diferenciales de primer orden separables

Ecuaciones diferenciales de primer orden

Ecuaciones diferenciales de primer orden Métodos Matemáticos - INAOE

Ecuaciones diferenciales de primer orden Métodos Matemáticos - INAOE

Ecuaciones diferenciales de primer orden Métodos Matemáticos - INAOE

Ejercicios: EJEMPLOS: Resolver las sig. EDO. Métodos Matemáticos - INAOE

CASO ESPECIAL DE SEPARACION DE VARIABLES El cambio de variable lleva a :

EJEMPLO

Ecuaciones diferenciales de primer orden EDO Exacta Se dice que una EDO es exacta cuando tiene la forma : … y su solución es: Se le llama “exacta” porque sale de construir la diferencial total de una función F:

Ejemplo: Ecuación diferencial de primer orden Exacta

SOLUCION : La premisa es que se trata de una EDO exacta : Si se cumple esta igualdad, si es una EDO exacta: Tomamos el 1 er. Término e integramos con respecto a “x” (y constante): Obtenemos derivada parcial con respecto a “y”: Despejamos g´(y) Integrando con respecto a “y” obtenemos g(y) Tomamos g(y) y lo substituimos en F LA SOLUCION DE LA EDO ES F=c

Ejemplo. Resolver:

Ejemplo: Resuelva la sig. EDO :

Ecuaciones diferenciales de primer orden Métodos Matemáticos - INAOE

Determinación del Factor integrante µ(x) Forma gral. de la EDO La escribimos en forma diferencial Multiplicamos todo por el factor integrante µ(x) Para convertir la EDO en exacta se debe cumplir que: Simplificando: Resolviendo para µ : Factor Integrante :

Solución de la EDO una vez conocido el factor integrante: A partir de la EDO en su forma diferencial: Multiplicamos todo por el factor integrante: Reconocemos del lado izquierdo la diferencial de un producto: Integramos en ambos lados: Despejando “y” tenemos la solución ! :

Ejemplo: EDO no homogénea 1 er. Orden, factor integrante

Ejemplo: EDO no homogénea 1 er. Orden, factor integrante

Ejemplo: Resolver EDO La EDO ya era exacta !!!

…para comprobar vamos a resolverla por EDO exacta:

METODO DE VARIACION DE PARAMETROS EN LA SOLUCION DE ECS. DIF. LINEAL NO-HOMOGENEA Sol. Complementaria es la sol. de la ec. homogénea asociada La solución particular proviene de la forma de f(x)

El método de variación de parámetros consiste en encontrar una función v(x) tal que al ser multiplicada por la solución complementaria entregue la solución de la ecuación diferencial Iniciamos con la forma gral. de la ecuación: Substituímos la sol. propuesta: Derivamos el producto: Agrupamos y cancelamos término: Resolvemos para “v” :

Integramos la expresión: Substituímos en la solución originalmente propuesta Se obtiene la solución: :

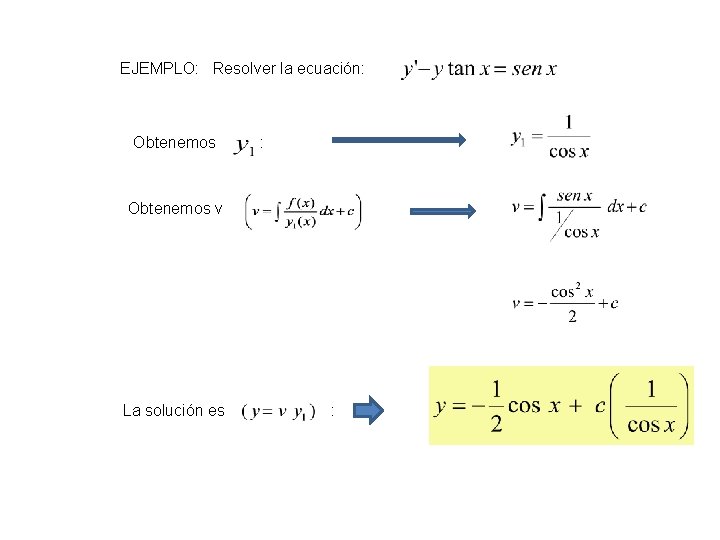
EJEMPLO: Resolver la ecuación: Sol. Complementaria es la sol. de la ec. homogénea asociada

EJEMPLO: Resolver la ecuación: Obtenemos v La solución es :

Ejemplo Ecuaciones no homogéneas: Variación de Parámetros (ejemplos). Métodos Matemáticos - INAOE

Ejemplo Ecuaciones no homogéneas: Variación de Parámetros (ejemplos). Métodos Matemáticos - INAOE

EDO de segundo orden Métodos Matemáticos - INAOE