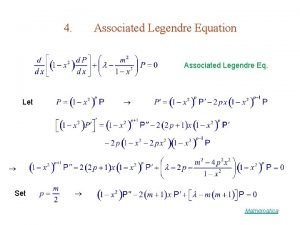Important Partial Differential Equations in curvilinear cdts Legendre









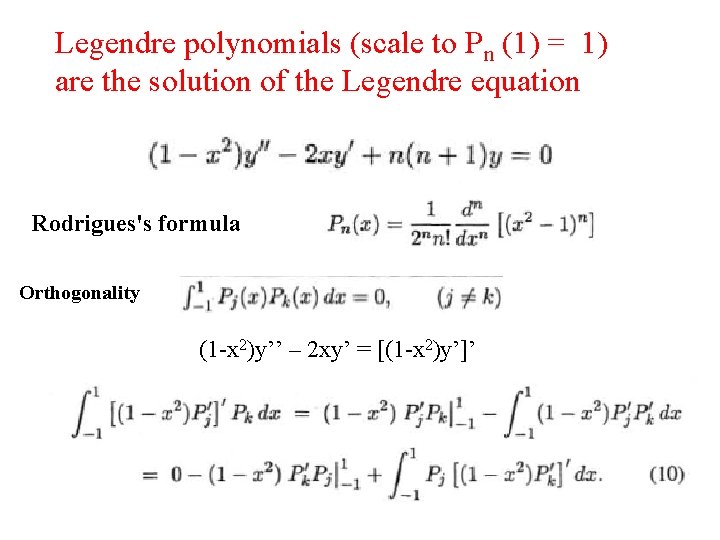
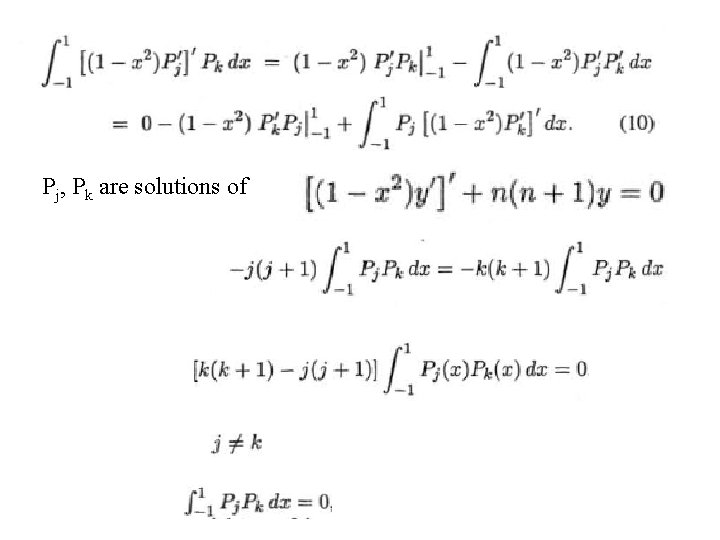




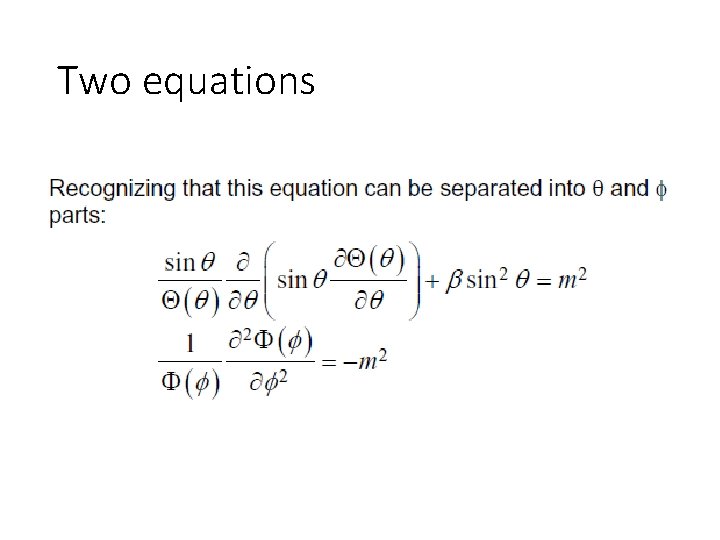

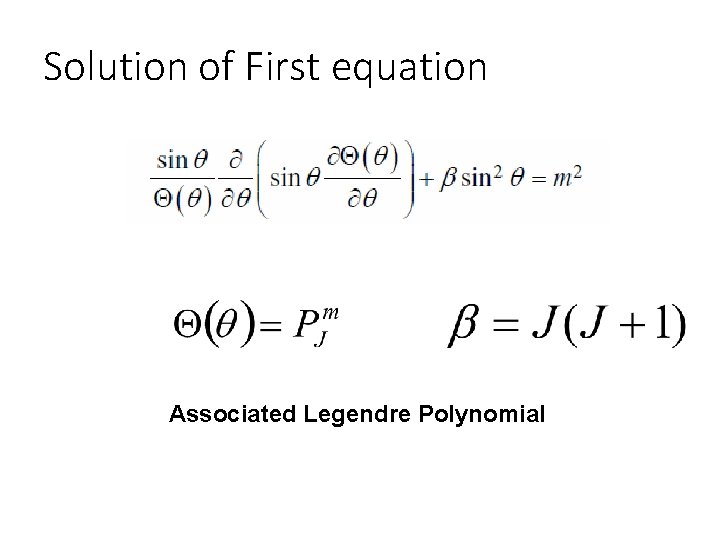

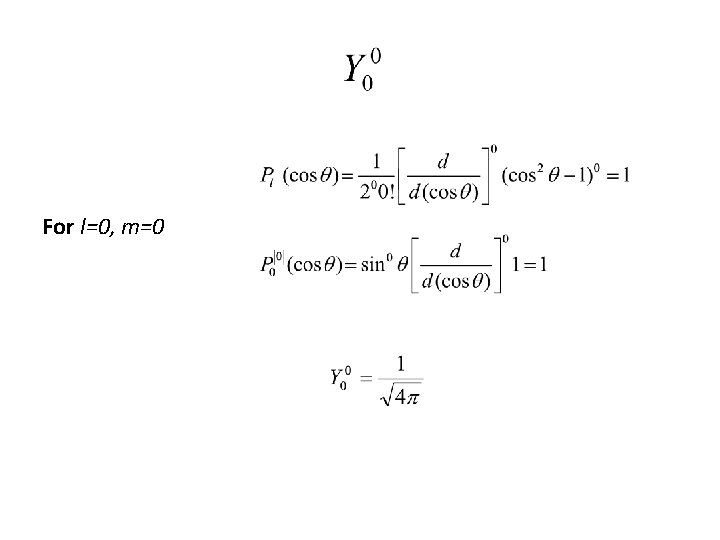

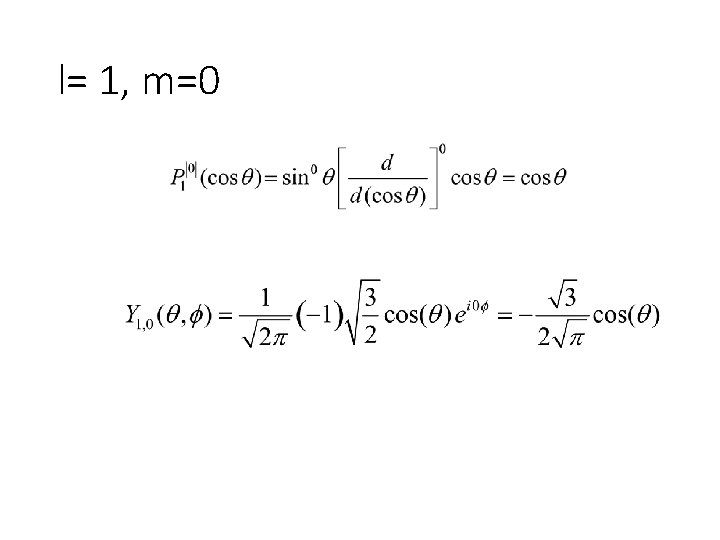




- Slides: 36

Important Partial Differential Equations- in curvilinear cdts












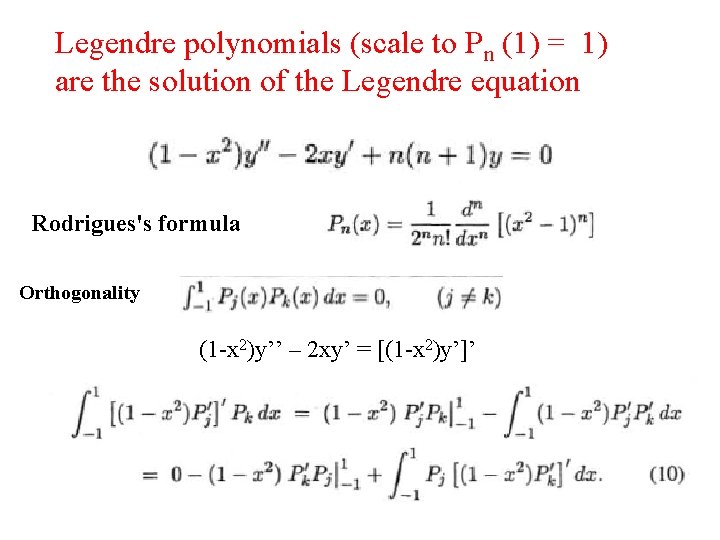
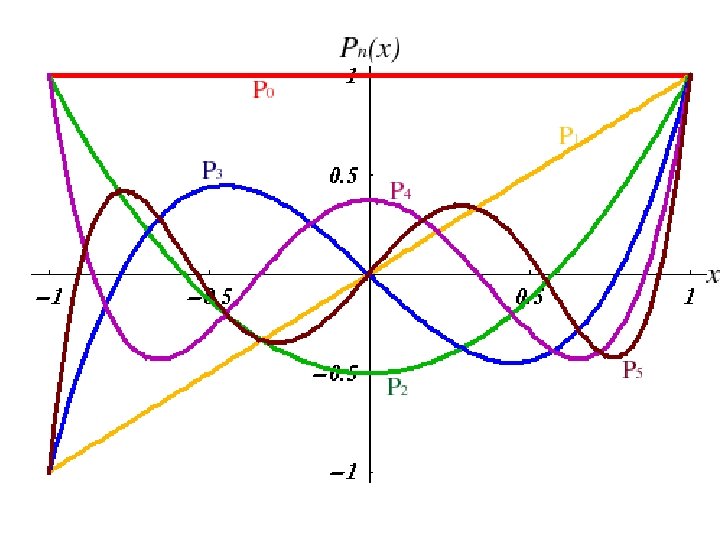
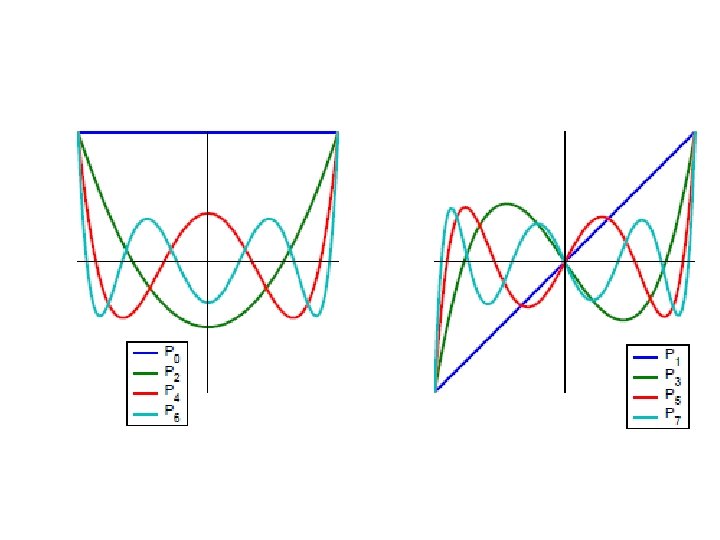
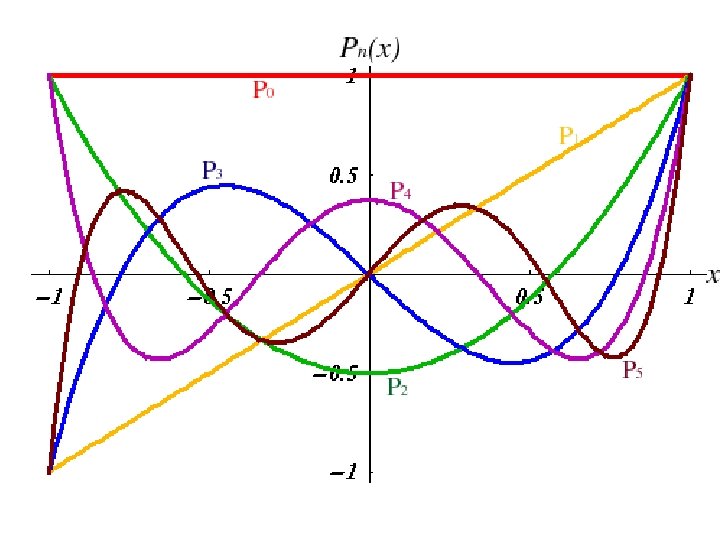
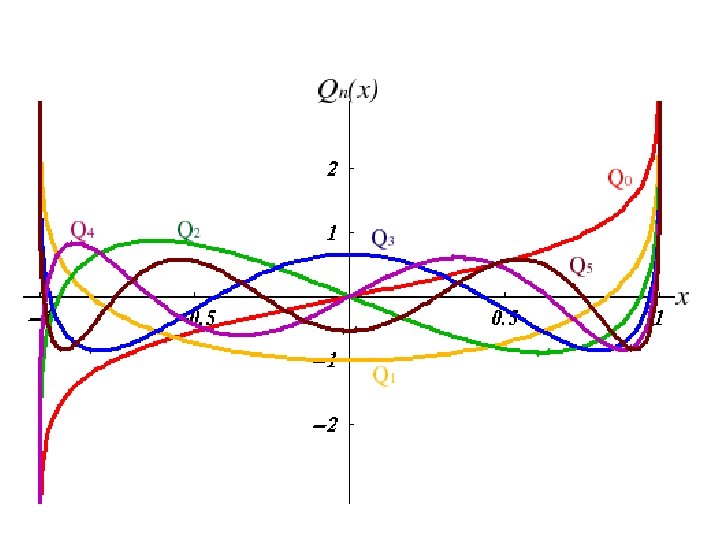
Legendre polynomials (scale to Pn (1) = 1) are the solution of the Legendre equation Rodrigues's formula Orthogonality (1 -x 2)y’’ – 2 xy’ = [(1 -x 2)y’]’
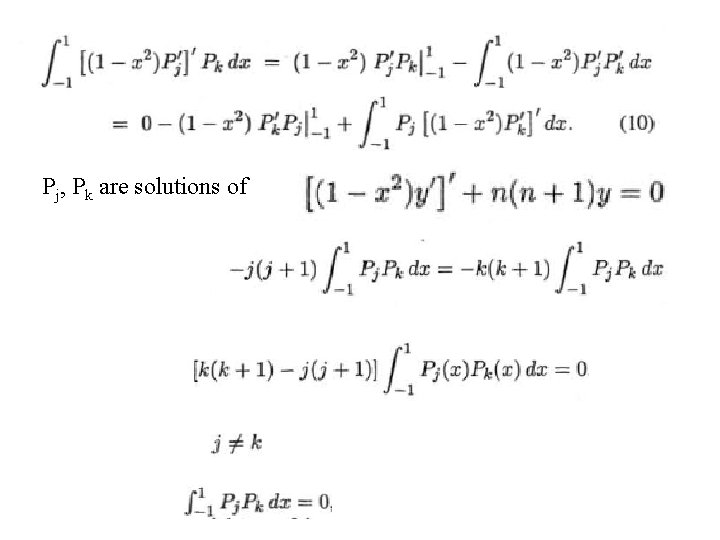
Pj, Pk are solutions of



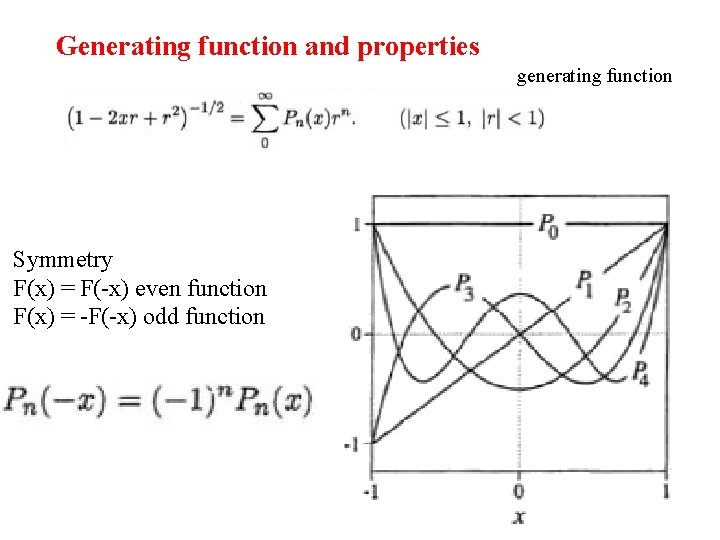
Generating function and properties generating function Symmetry F(x) = F(-x) even function F(x) = -F(-x) odd function

Taking partial derivative w/r to r Taking partial derivative w/r to x Finally the case, i = j = n

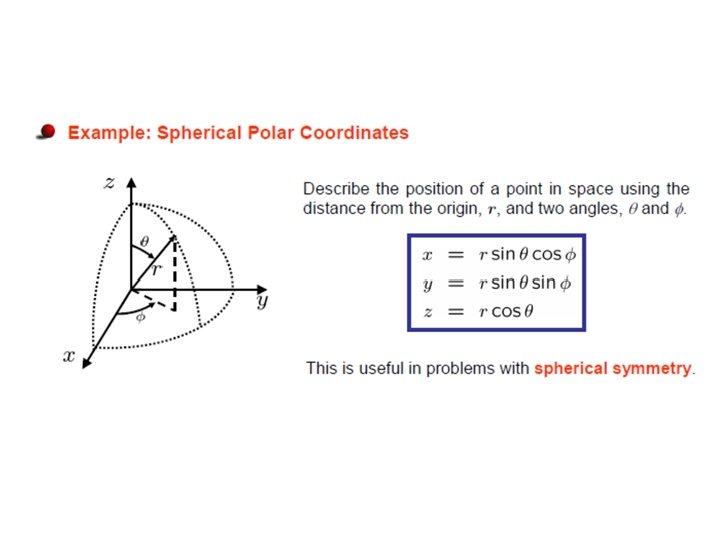
Rigid Rotor in Quantum Mechanics Transition from the above classical expression to quantum mechanics can be carried out by replacing the total angular momentum by the corresponding operator: Wave functions must contain both θ and Φ dependence: are called spherical harmonics

Schrondinger equation

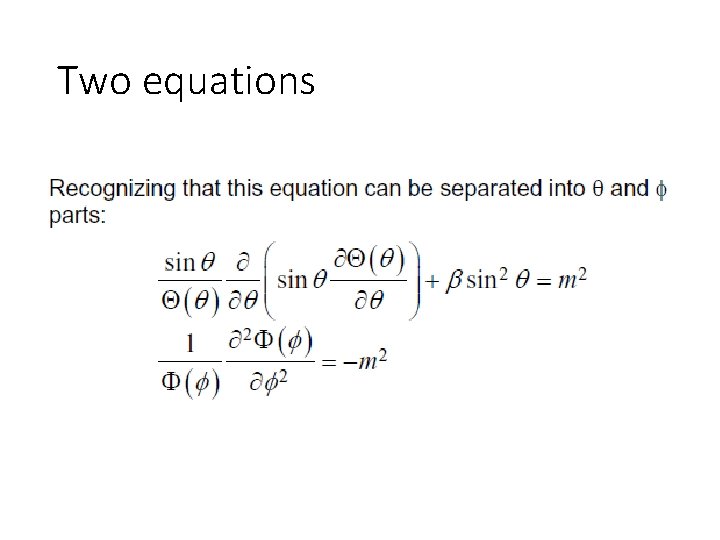
Two equations

Solution of second equation
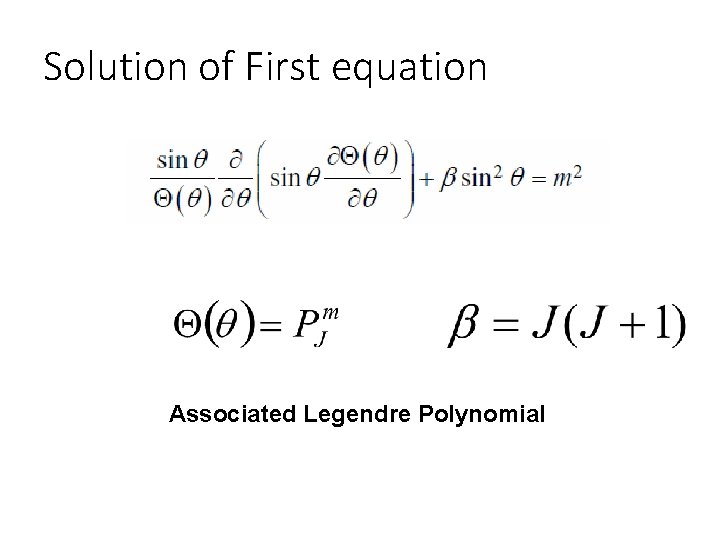
Solution of First equation Associated Legendre Polynomial

Associated Legendre Polynomial
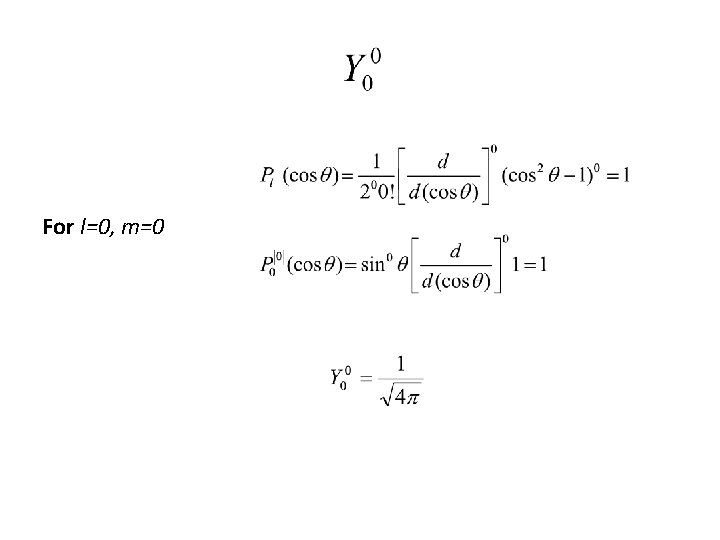
For l=0, m=0

First spherical harmonics Spherical Harmonic, Y 0, 0
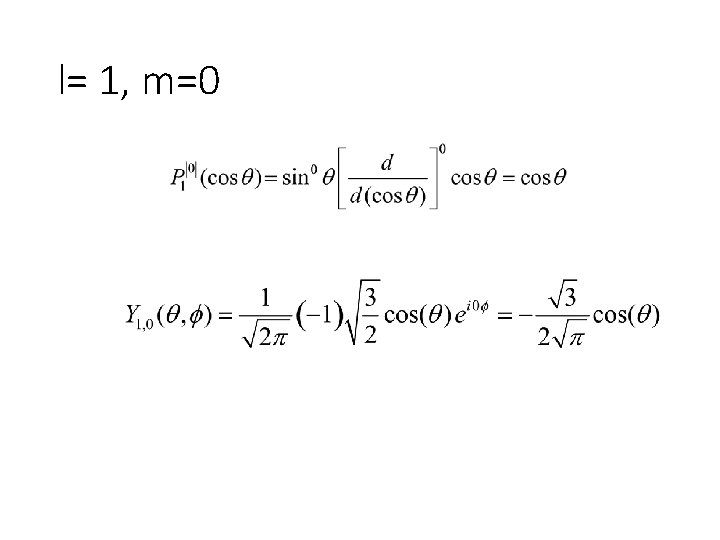
l= 1, m=0

l= 1, m=0 θ cos 2θ 0 1 30 3/4 45 1/2 60 1/4 90 0

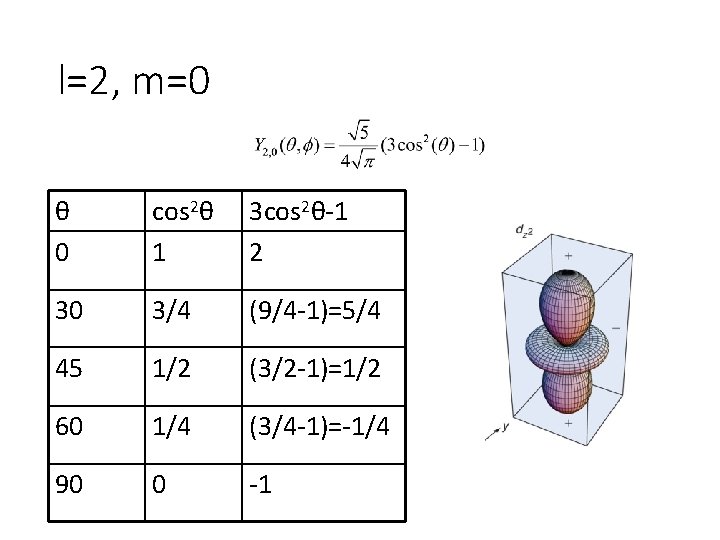
l=2, m=0 θ 0 cos 2θ 1 3 cos 2θ-1 2 30 3/4 (9/4 -1)=5/4 45 1/2 (3/2 -1)=1/2 60 1/4 (3/4 -1)=-1/4 90 0 -1

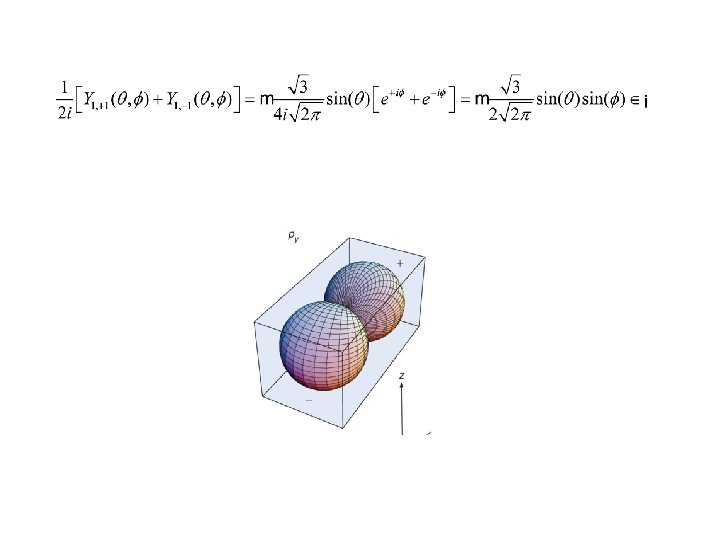
l = 1, m=± 1 Complex Value? ? If Ф 1 and Ф 2 are degenerateeigenfunctions, their linear combinations are also an eigenfunction with the same eigenvalue.

l=1, m=± 1 Along x-axis



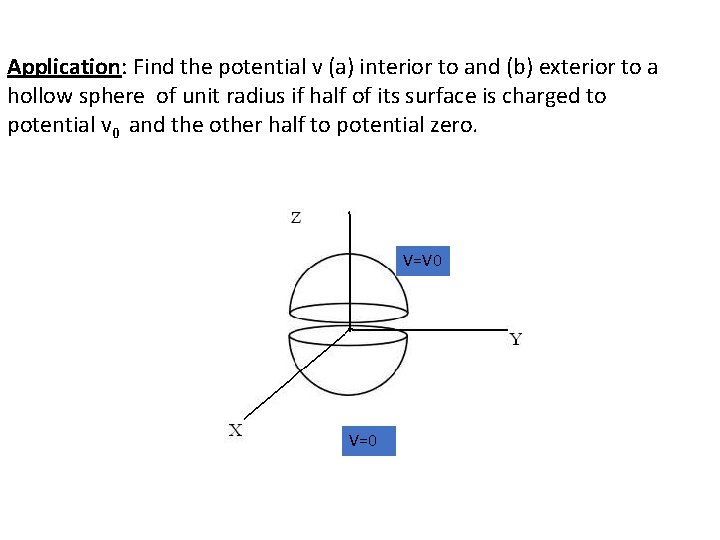
Application: Find the potential v (a) interior to and (b) exterior to a hollow sphere of unit radius if half of its surface is charged to potential v 0 and the other half to potential zero. V=V 0 V=0
 What are cdts
What are cdts Central force
Central force Ppt on differential equations
Ppt on differential equations Characteristics method partial differential equations
Characteristics method partial differential equations Differential equations definition
Differential equations definition Integration of partial differential equation
Integration of partial differential equation Ordinary differential equations
Ordinary differential equations Hyperbolic partial differential equation
Hyperbolic partial differential equation Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth First order condition
First order condition Curvilinear motion cylindrical components
Curvilinear motion cylindrical components Partial differential protection
Partial differential protection General solution of partial differential equation
General solution of partial differential equation Classification of pde
Classification of pde Pde
Pde The solution of partial differential equation
The solution of partial differential equation Quadratura de gauss-legendre
Quadratura de gauss-legendre Polinomios de legendre
Polinomios de legendre Manon legendre
Manon legendre Gauss kareleme yöntemi
Gauss kareleme yöntemi Matthieu legendre
Matthieu legendre Identidad de legendre
Identidad de legendre Legendre polynomials
Legendre polynomials Schlaefli integral
Schlaefli integral Edmond laguerre
Edmond laguerre Sofya kovalevskaya (1850 – 1891)
Sofya kovalevskaya (1850 – 1891) Canonical transformation
Canonical transformation Matlab legendre polynomial
Matlab legendre polynomial In plane motion the rotation and translation would be
In plane motion the rotation and translation would be Curvilinear translation
Curvilinear translation What is instantaneous centre
What is instantaneous centre Curvilinear line
Curvilinear line N-t coordinate system
N-t coordinate system Curvilinear motion formulas
Curvilinear motion formulas Curvilinear cost graph
Curvilinear cost graph Planar kinematics of a rigid body
Planar kinematics of a rigid body Curvilinear translation
Curvilinear translation