Differential Equations MTH 242 Lecture 29 Dr Manshoor






















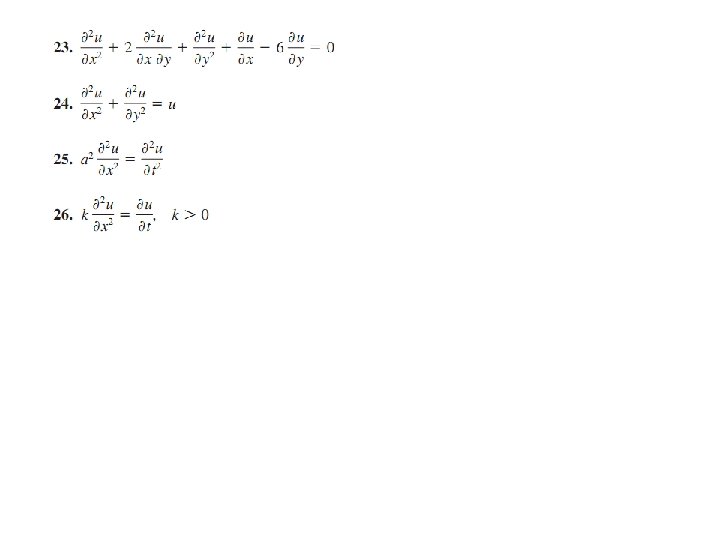

- Slides: 24

Differential Equations MTH 242 Lecture # 29 Dr. Manshoor Ahmed

Summary(Recall) • Homogeneous system of linear DEs. • Eigenvalue and Eigenvector. • Solution of system when eigenvalues real and distinct. • Solution of system when eigenvalues complex. • Solution of system when eigenvalues real and repeated

Partial Differential Equations

Motivation Most physical phenomena, whether in the domain of fluid dynamics, electricity, magnetism, mechanics, optics or heat flow, can be in general (and actually are) described by partial differential equations.

What is a Partial Differential Equation? A partial differential equation (PDE) is an equation that has a unknown function of more than one variable and contains some partial derivatives of unknown function.

Basic Classifications of PDEs. Order of the PDE The order of a PDE is the order of the highest partial derivative in the equation. Examples

Number of variables PDEs may be classified by the number of their independent variables, that is, the number of variables the unknown function depends on. Examples

Linearity Partial differential equations (PDEs), like ordinary differential equations (ODEs), can also be classified as either linear or nonlinear. Analogous to a linear ODE, the dependent variable and its partial derivatives in a linear PDE are only to the first power. However, in this course we shall be interested in, for the most part, linear second-order PDEs. Examples

Kinds of coefficients PDE can be with constant or variable coefficients (if at least one of the coefficients is a function of (some of) independent variables). Examples

Homogeneity PDE is homogeneous if the free term (the right-hand side term) is zero. Examples

Classifications of Second-order linear PDEs. A second-order linear PDE in two variables can be in general written in the following form where A, B, C, D, E, and F are coefficients, and G is a non-homogeneous (or right-hand side) term. All the coefficients are real constants. This equation is said to be hyperbolic if parabolic if elliptic if

Examples 1. Hyperbolic 2. Parabolic 3. Elliptic

Physical situations where these PDEs appear The mathematical solutions to these three types of equations are quite different. The three major classifications of linear PDEs essentially classify physical problems into three basic types: 1. vibrating systems and wave propagation, conservation laws (hyperbolic ), 2. heat flow and diffusion processes (parabolic), 3. steady-state phenomena (elliptic case).

Solution of a PDE A solution of a linear partial differential equation is a function u(x, y) of two independent variables that possesses all partial derivatives occurring in the equation and that satisfies the equation in some region of the xy-plane. Note It is often difficult to find the general solutions of a linear partial differential equations. But, a general solution is usually not all that useful in applications. Thus our focus throughout will be on finding particular solutions of some of the more important linear PDEs that is, equations that appear in many applications.


Example to illustrate the method of separation of variables:




Superposition principle

Exercises for practice In Problems 1 – 16 use separation of variables to find, if possible, product solutions for the given partial differential equation.

In Problems 17– 26 classify the given partial differential equation as hyperbolic, parabolic, or elliptic.
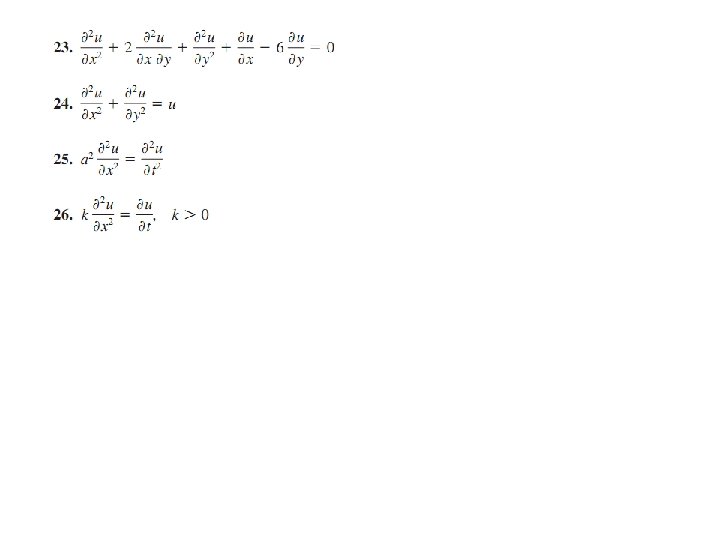

Summary • Partial Differential Equations. • Motivation and definition. • Classification (order, number of variables, linearity etc). • Classification of second order linear PDEs (hyperbolic, parabolic and elliptic). • Solution of a PDE. • Method of separation of variables. • Superposition principle. • Examples.