13 Gamma Function 1 Definitions Properties 2 Digamma

13. Gamma Function 1. Definitions, Properties 2. Digamma & Polygamma Functions 3. The Beta Function 4. Sterling’s Series 5. Riemann Zeta Function 6. Other Related Functions

Peculiarities: 1. Do not satisfy any differential equation with rational coefficients. 2. Not a hypergeometric nor a confluent hypergeometric function. Common occurence: In expansion coefficients.

13. 1. Definitions, Properties Definition, infinite limit (Euler) version :

Definition: Definite Integral Definition, definite integral (Euler) version : , else singular at t = 0.

Equivalence of the Limit & Integral Definitions Consider

Definition: Infinite Product (Weierstrass Form) Definition, Infinite Product (Weierstrass) version : Euler-Mascheroni constant Proof :

Functional Relations Reflection formula : ( about z = ½ ) Proof : Let

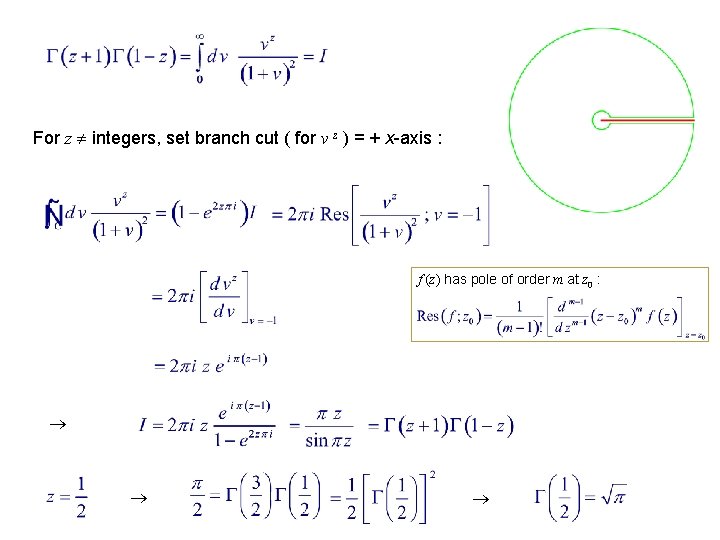
For z integers, set branch cut ( for v z ) = + x-axis : f (z) has pole of order m at z 0 :

Legendre’s Duplication Formula General proof in § 13. 3. Proof for z = n = 1, 2, 3, …. : ( Case z = 0 is proved by inspection. )

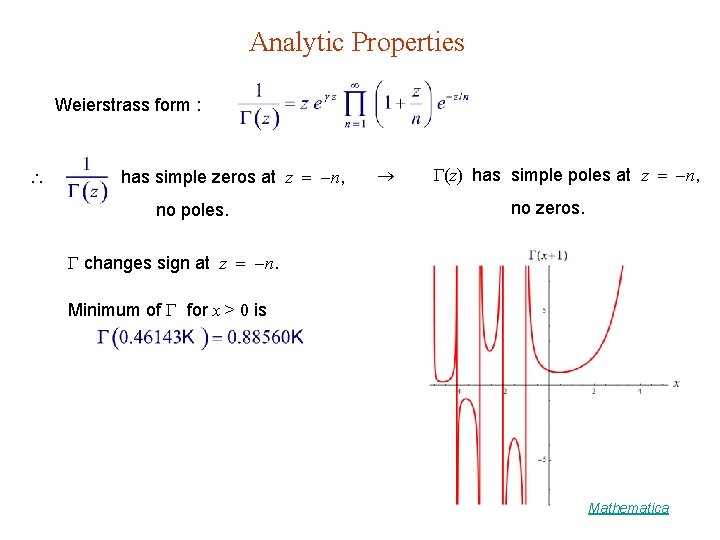
Analytic Properties Weierstrass form : has simple zeros at z n, no poles. (z) has simple poles at z n, no zeros. changes sign at z n. Minimum of for x > 0 is Mathematica

Residues at z n Residue at simple pole z n is n+1 times :

Schlaefli Integral Schlaefli integral : C 1 is an open contour. ( e t for Re t . Branch-cut. ) Proof : if > 1

where For Re > 1, ID = 0 reproduces the integral represention. For Re < 1 , IA , IB , & ID are all singular. However, remains finite. ( integrand regular everywhere on C ) is valid for all . Factorial function : (z) is the Gauss’ notation

Example 13. 1. 1 Maxwell-Boltzmann Distribution Classical statistics (for distinguishable particles) : Probability of state of energy E being occupied is Maxwell-Boltzmann distribution Partition function Average energy : g(E) = density of states Ideal gas : gamma distribution

13. 2. Digamma & Polygamma Functions Digamma function : 50 digits z = integer : Mathematica

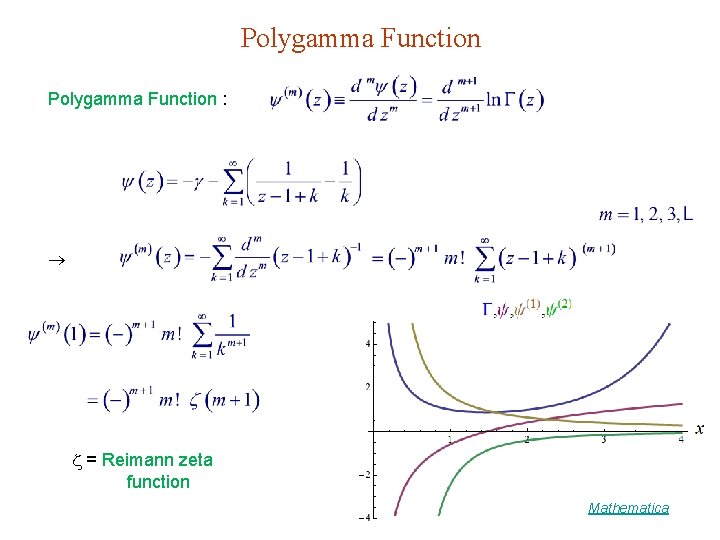
Polygamma Function : = Reimann zeta function Mathematica

Maclaurin Expansion of ln Converges for Stirling’s series ( § 13. 4 ) has a better convergence.

Series Summation Example 13. 2. 1. Catalan’s Constant Dirichlet series : Catalan’s Constant : 20 digits Mathematica

13. 3. The Beta Function :

Alternate Forms : Definite Integrals To be used in integral rep. of Bessel (Ex. 14. 1. 17) & hypergeometric (Ex. 18. 5. 12) functions

Derivation: Legendre Duplication Formula