Use of moment generating functions 1 Using the









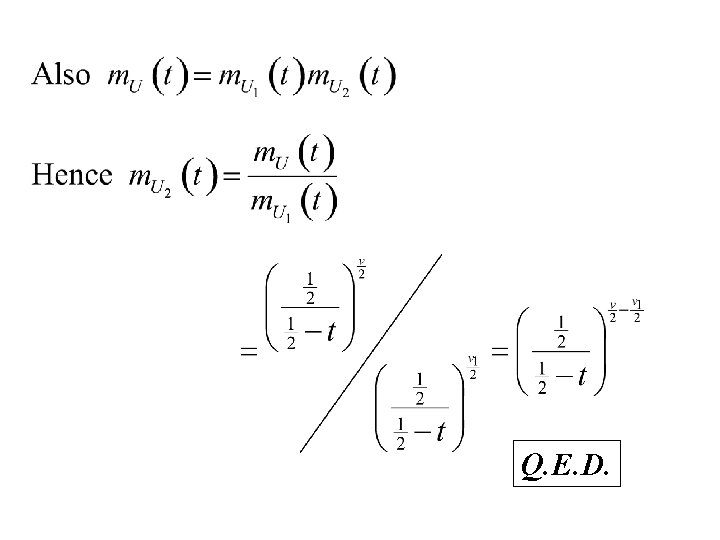


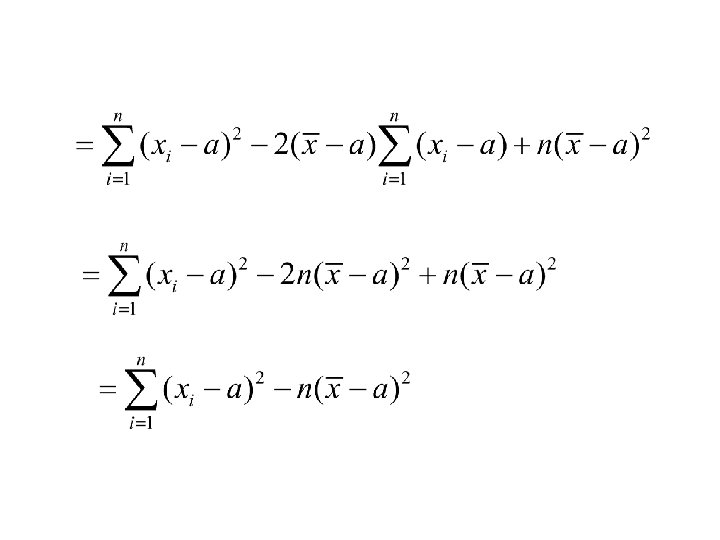

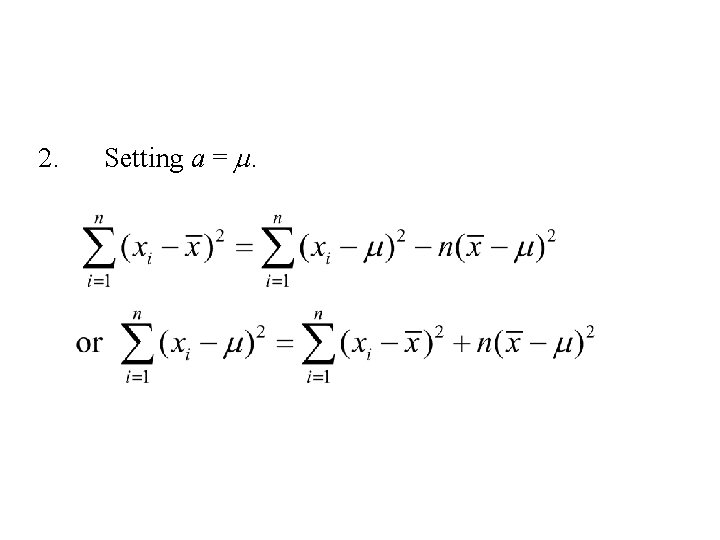







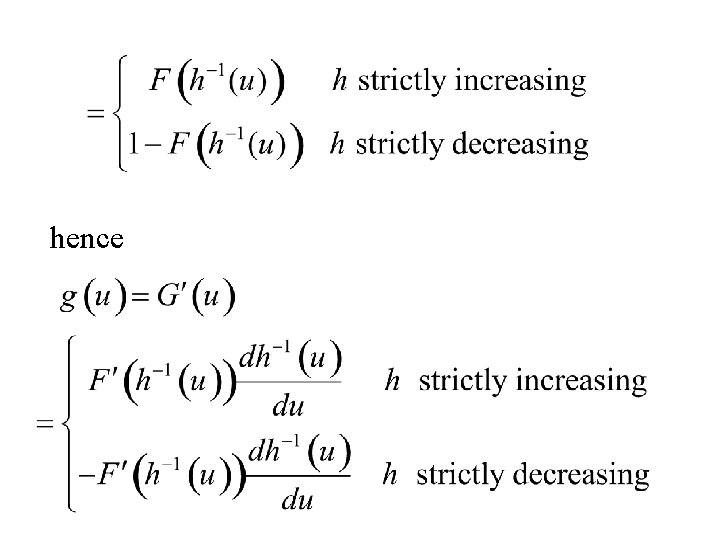
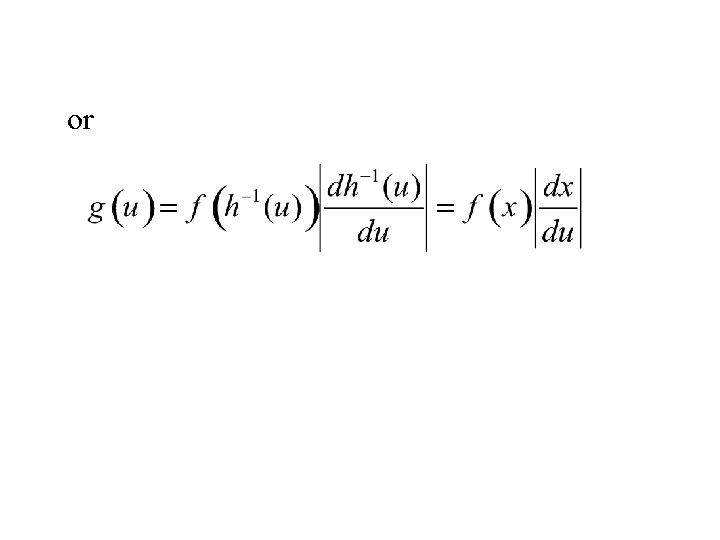








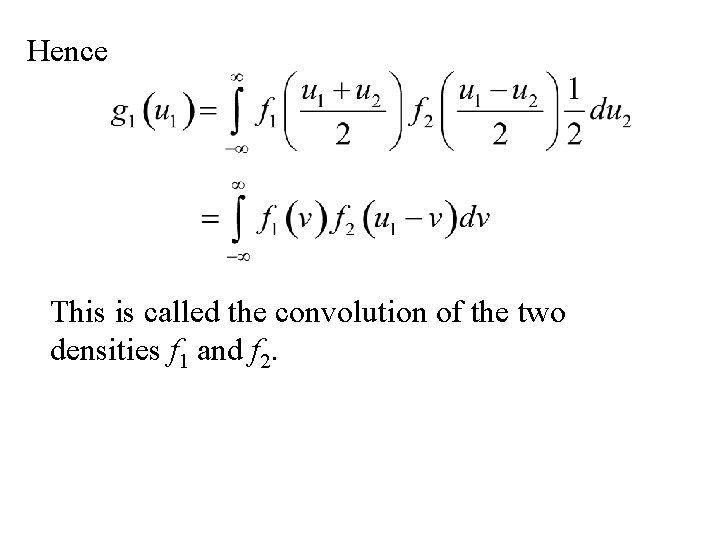

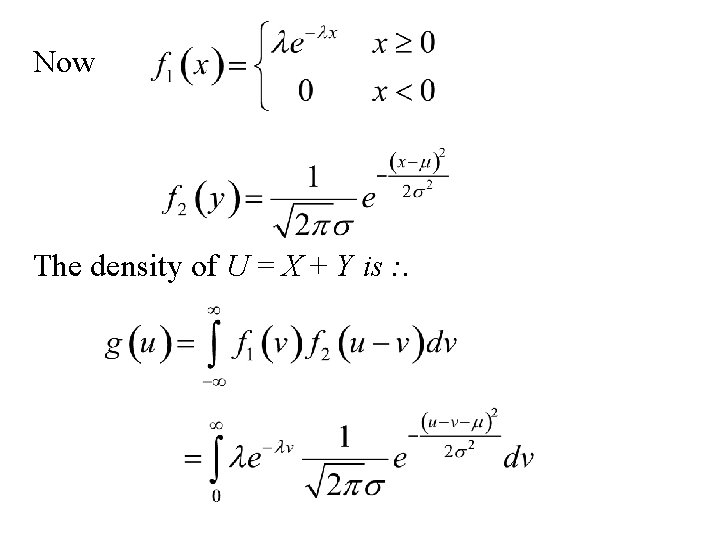
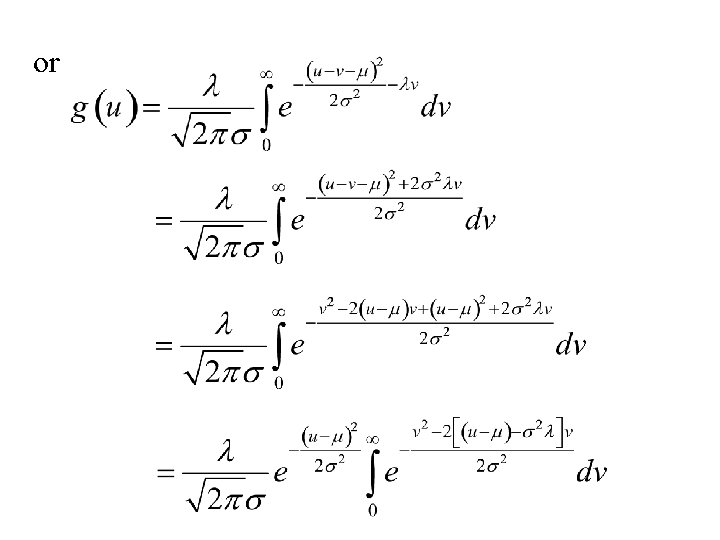
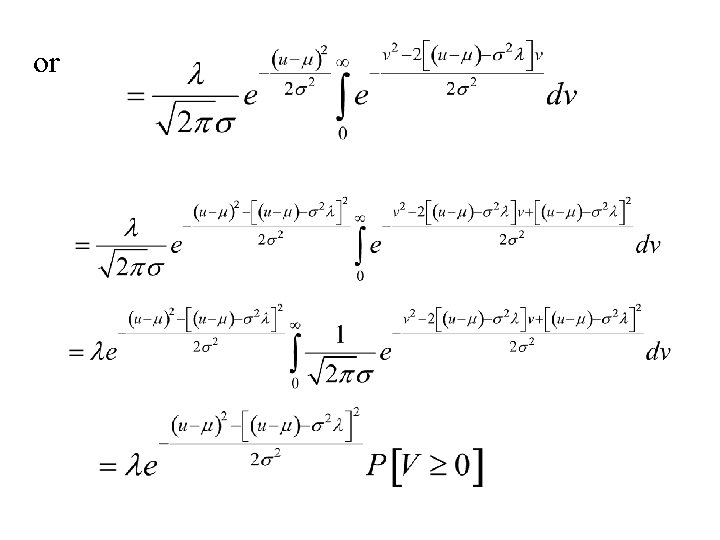

- Slides: 40

Use of moment generating functions 1. Using the moment generating functions of X, Y, Z, …determine the moment generating function of W = h(X, Y, Z, …). 2. Identify the distribution of W from its moment generating function This procedure works well for sums, linear combinations etc.

Therorem Let X and Y denote a independent random variables each having a gamma distribution with parameters (l, a 1) and (l, a 2). Then W = X + Y has a gamma distribution with parameters (l, a 1 + a 2). Proof:

Recognizing that this is the moment generating function of the gamma distribution with parameters (l, a 1 + a 2) we conclude that W = X + Y has a gamma distribution with parameters (l, a 1 + a 2).

Therorem (extension to n RV’s) Let x 1, x 2, … , xn denote n independent random variables each having a gamma distribution with parameters (l, ai), i = 1, 2, …, n. Then W = x 1 + x 2 + … + xn has a gamma distribution with parameters (l, a 1 + a 2 +… + an). Proof:

Therefore Recognizing that this is the moment generating function of the gamma distribution with parameters (l, a 1 + a 2 +…+ an) we conclude that W = x 1 + x 2 + … + xn has a gamma distribution with parameters (l, a 1 + a 2 +…+ an).

Therorem Suppose that x is a random variable having a gamma distribution with parameters (l, a). Then W = ax has a gamma distribution with parameters (l/a, a). Proof:

Special Cases 1. Let X and Y be independent random variables having a c 2 distribution with n 1 and n 2 degrees of freedom respectively then X + Y has a c 2 distribution with degrees of freedom n 1 + n 2. 2. Let x 1, x 2, …, xn, be independent random variables having a c 2 distribution with n 1 , n 2 , …, nn degrees of freedom respectively then x 1+ x 2 +…+ xn has a c 2 distribution with degrees of freedom n 1 +…+ nn. Both of these properties follow from the fact that a c 2 random variable with n degrees of freedom is a G random variable with l = ½ and a = n/2.

Recall If z has a Standard Normal distribution then z 2 has a c 2 distribution with 1 degree of freedom. Thus if z 1, z 2, …, zn are independent random variables each having Standard Normal distribution then has a c 2 distribution with n degrees of freedom.

Therorem Suppose that U 1 and U 2 are independent random variables and that U = U 1 + U 2 Suppose that U 1 and U have a c 2 distribution with degrees of freedom n 1 andn respectively. (n 1 < n) Then U 2 has a c 2 distribution with degrees of freedom n 2 =n -n 1 Proof:
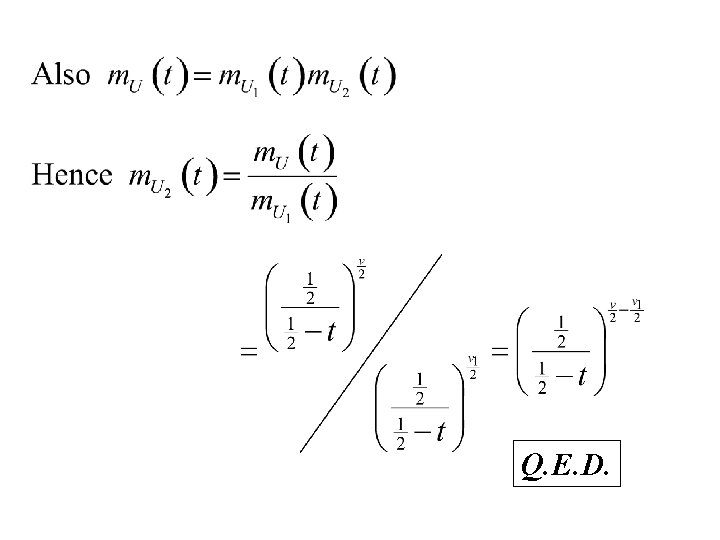
Q. E. D.

Distribution of the sample variance

Properties of the sample variance Proof:
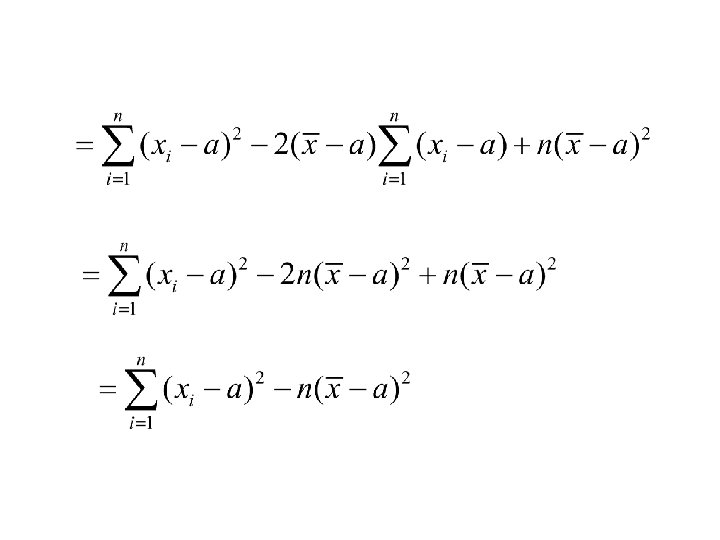

Special Cases 1. Setting a = 0. Computing formula
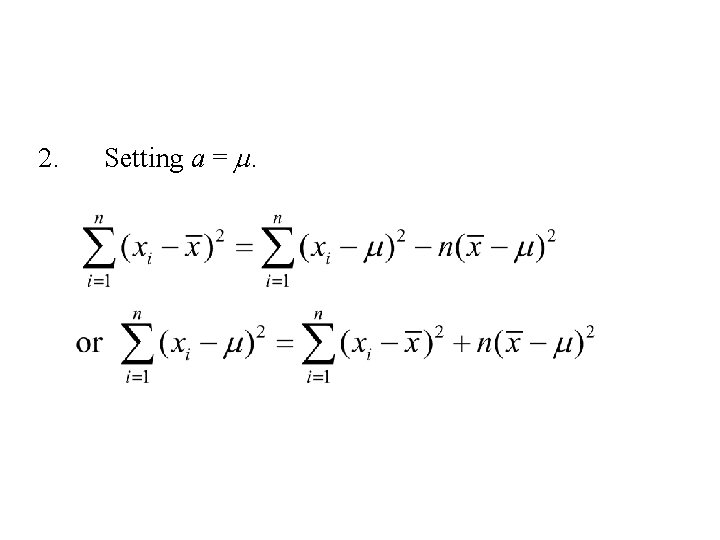
2. Setting a = m.

Distribution of the sample variance Let x 1, x 2, …, xn denote a sample from the normal distribution with mean m and variance s 2. Let Then has a c 2 distribution with n degrees of freedom.

Note: or U = U 2 + U 1 has a c 2 distribution with n degrees of freedom.

We also know that has normal distribution with mean m and variance s 2/n Thus has a Standard Normal distribution and has a c 2 distribution with 1 degree of freedom.

If we can show that U 1 and U 2 are independent then has a c 2 distribution with n - 1 degrees of freedom. The final task would be to show that are independent

Summary Let x 1, x 2, …, xn denote a sample from the normal distribution with mean m and variance s 2. 1. than has normal distribution with mean m and variance s 2/n 2. has a c 2 distribution with n = n - 1 degrees of freedom.

The Transformation Method Theorem Let X denote a random variable with probability density function f(x) and U = h(X). Assume that h(x) is either strictly increasing (or decreasing) then the probability density of U is:

Proof Use the distribution function method. Step 1 Find the distribution function, G(u) Step 2 Differentiate G (u ) to find the probability density function g(u)
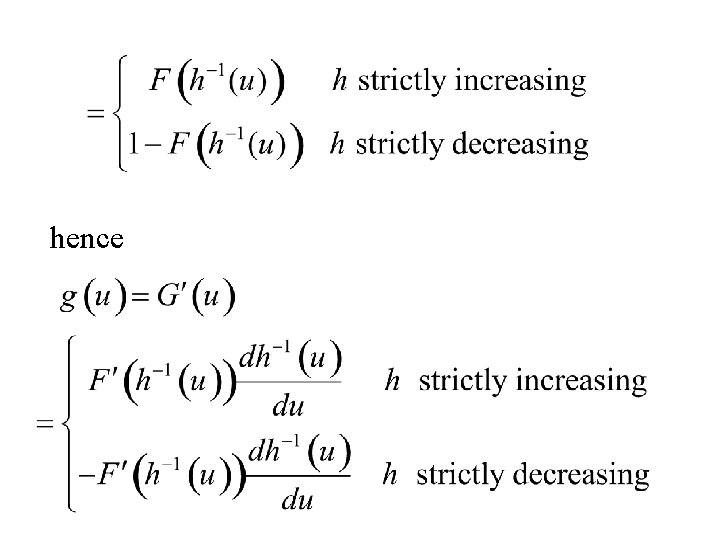
hence
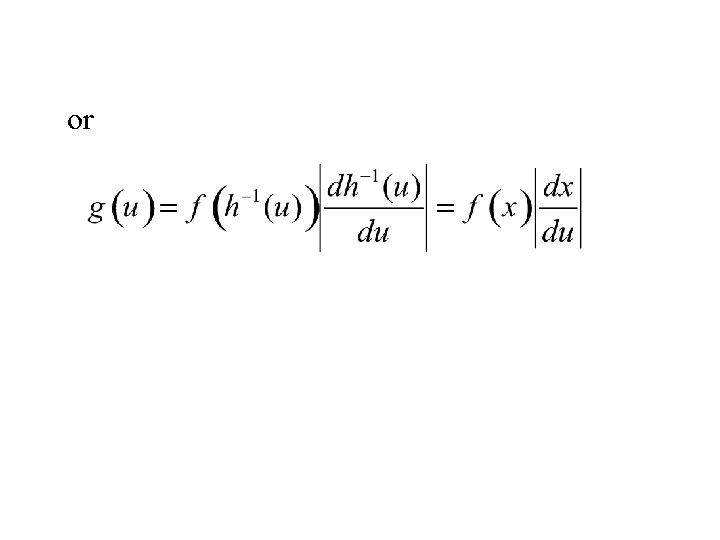
or

Example Suppose that X has a Normal distribution with mean m and variance s 2. Find the distribution of U = h(x) = e. X. Solution:

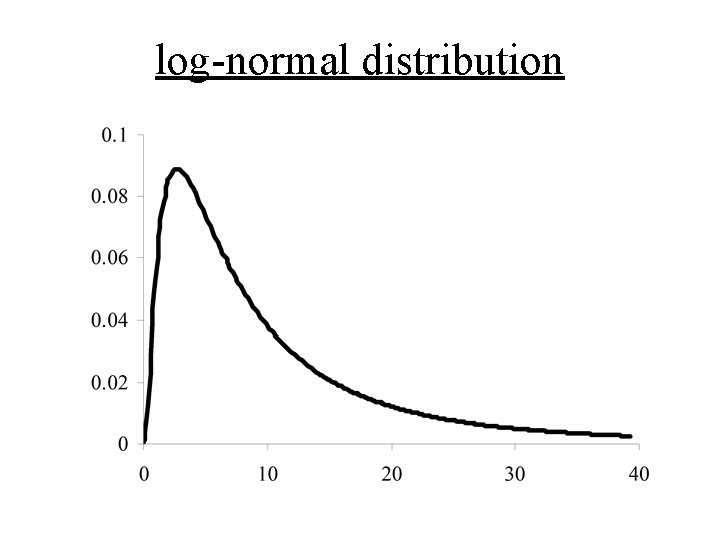
hence This distribution is called the log-normal distribution

log-normal distribution

The Transfomation Method (many variables) Theorem Let x 1, x 2, …, xn denote random variables with joint probability density function f(x 1, x 2, …, xn ) Let u 1 = h 1(x 1, x 2, …, xn). u 2 = h 2(x 1, x 2, …, xn). un = hn(x 1, x 2, …, xn). define an invertible transformation from the x’s to the u’s

Then the joint probability density function of u 1, u 2, …, un is given by: where Jacobian of the transformation

Example Suppose that x 1, x 2 are independent with density functions f 1 (x 1) and f 2(x 2) Find the distribution of u 1 = x 1+ x 2 u 2 = x 1 - x 2 Solving for x 1 and x 2 we get the inverse transformation

The Jacobian of the transformation

The joint density of x 1, x 2 is f(x 1, x 2) = f 1 (x 1) f 2(x 2) Hence the joint density of u 1 and u 2 is:

From We can determine the distribution of u 1= x 1 + x 2
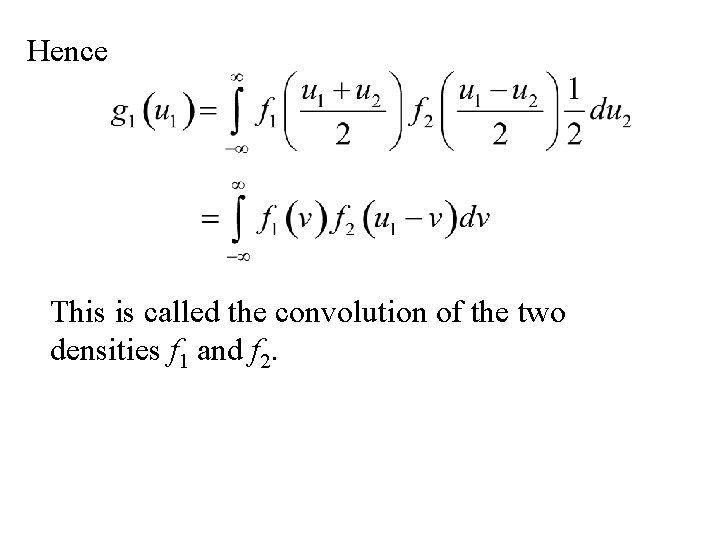
Hence This is called the convolution of the two densities f 1 and f 2.

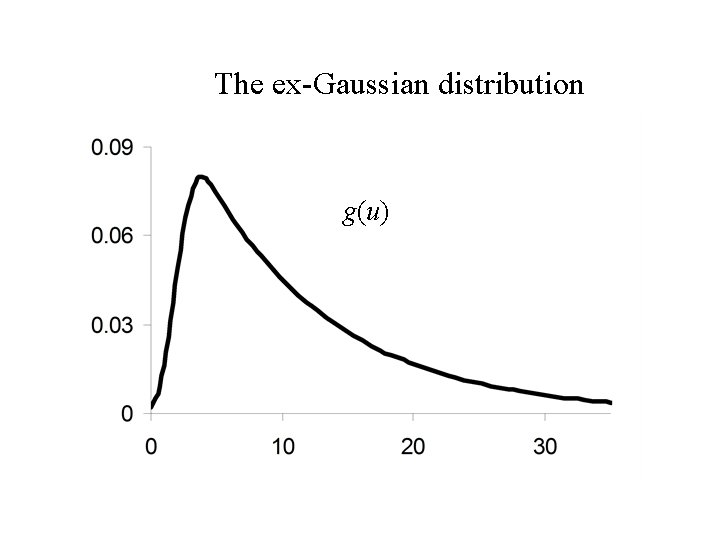
Example: The ex-Gaussian distribution Let X and Y be two independent random variables such that: 1. X has an exponential distribution with parameter l. 2. Y has a normal (Gaussian) distribution with mean m and standard deviation s. Find the distribution of U = X + Y. This distribution is used in psychology as a model for response time to perform a task.
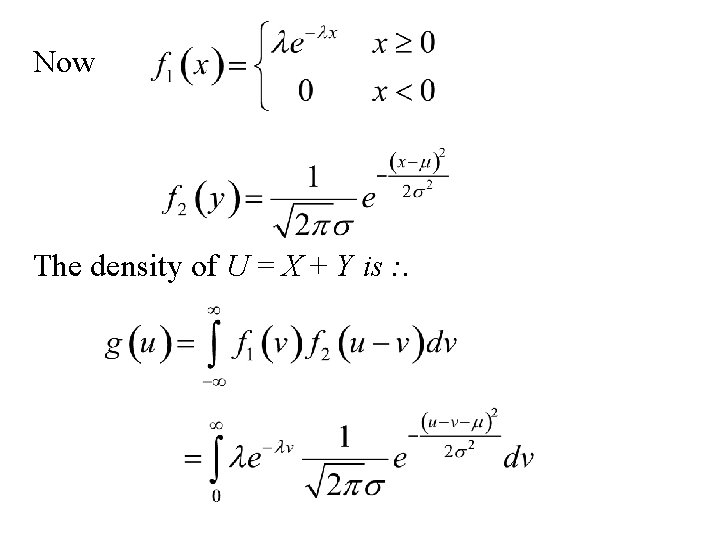
Now The density of U = X + Y is : .
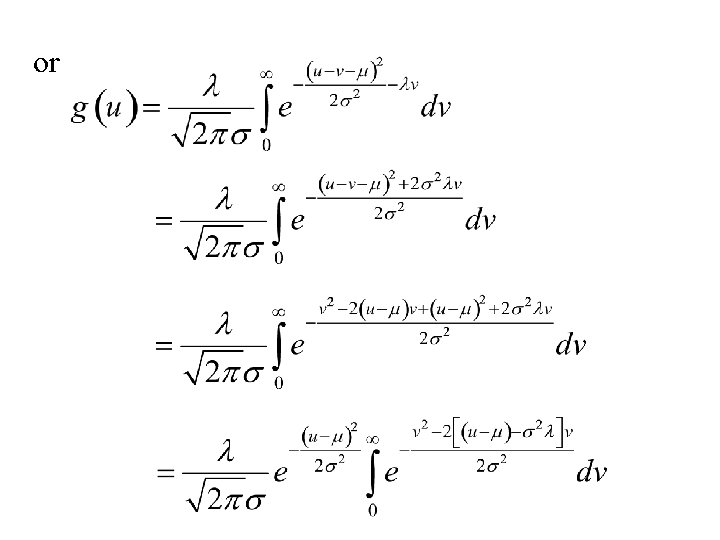
or
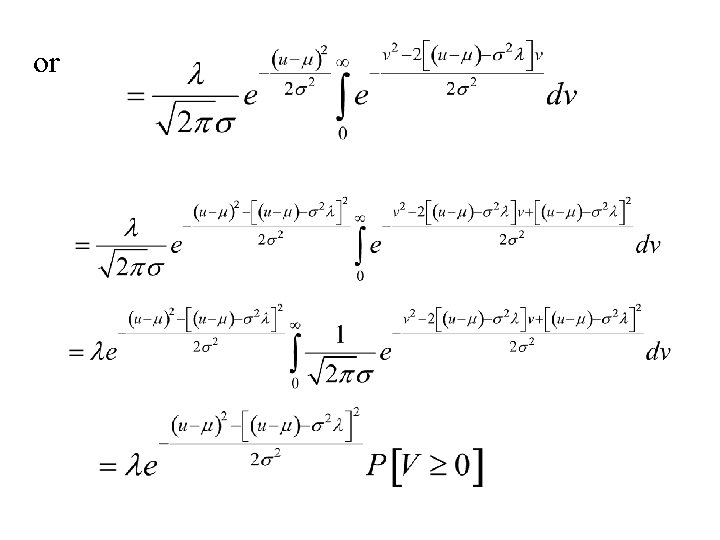
or

Where V has a Normal distribution with mean and variance s 2. Hence Where F(z) is the cdf of the standard Normal distribution

The ex-Gaussian distribution g(u)
 Mgf of normal distribution
Mgf of normal distribution Cumulant generating function of binomial distribution
Cumulant generating function of binomial distribution Characteristic function of negative binomial distribution
Characteristic function of negative binomial distribution Moment generating function of normal distribution
Moment generating function of normal distribution Moment generating function of normal distribution
Moment generating function of normal distribution Gamma function
Gamma function Calculating coefficients of generating functions
Calculating coefficients of generating functions Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Tư thế worm breton là gì
Tư thế worm breton là gì Chúa yêu trần thế
Chúa yêu trần thế Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Phép trừ bù
Phép trừ bù độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V. c c
V. c c Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Phối cảnh
Phối cảnh Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể Số nguyên tố là số gì
Số nguyên tố là số gì Tư thế ngồi viết
Tư thế ngồi viết





























































