SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Uniform Normal Exponential Gamma

SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Uniform, Normal, Exponential, Gamma and Chi-Square Distributions 1

Uniform Distribution – A random variable X is said to be uniformly distributed if its density function is – The expected value and the variance are 2

Indicator functions • It is sometimes convenient to express the p. m. f. or p. d. f. by using indicator functions. This is especially true when the range of random variable depends on a parameter. • Ex: Uniform distribution 3

Uniform Distribution • Example 1 – The daily sale of gasoline is uniformly distributed between 2, 000 and 5, 000 gallons. Find the probability that sales are: – Between 2, 500 and 3, 000 gallons – More than 4, 000 gallons – Exactly 2, 500 gallons f(x) = 1/(5000 -2000) = 1/3000 for x: [2000, 5000] P(2500 X 3000) = (3000 -2500)(1/3000) =. 1667 1/3000 25003000 5000 x 4

Uniform Distribution • Example 1 – The daily sale of gasoline is uniformly distributed between 2, 000 and 5, 000 gallons. Find the probability that sales are: – Between 2, 500 and 3, 500 gallons – More than 4, 000 gallons – Exactly 2, 500 gallons f(x) = 1/(5000 -2000) = 1/3000 for x: [2000, 5000] P(X 4000) = (5000 -4000)(1/3000) =. 333 1/3000 2000 4000 5000 x 5

Uniform Distribution • Example 1 – The daily sale of gasoline is uniformly distributed between 2, 000 and 5, 000 gallons. Find the probability that sales are: – Between 2, 500 and 3, 500 gallons – More than 4, 000 gallons – Exactly 2, 500 gallons f(x) = 1/(5000 -2000) = 1/3000 for x: [2000, 5000] P(X=2500) = (2500 -2500)(1/3000) = 0 1/3000 2500 5000 x 6

Normal Distribution • This is the most popular continuous distribution. – Many distributions can be approximated by a normal distribution. – The normal distribution is the cornerstone distribution of statistical inference. 7

Normal Distribution • A random variable X with mean and variance 2 is normally distributed if its probability density function is given by 8

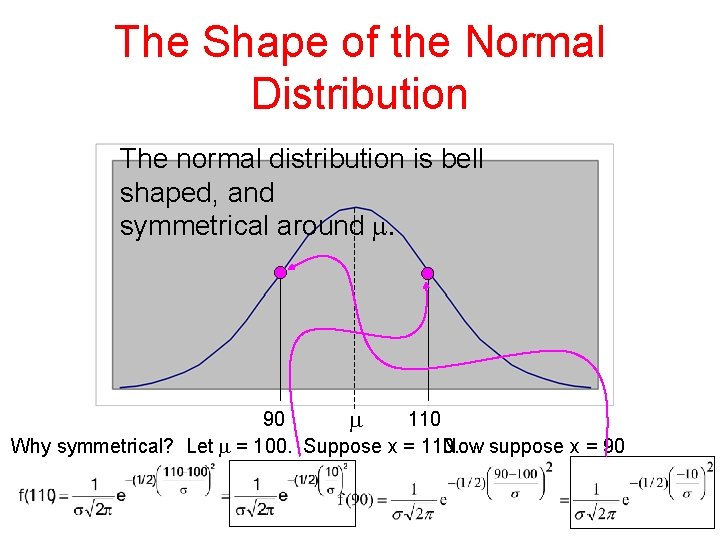
The Shape of the Normal Distribution The normal distribution is bell shaped, and symmetrical around . 90 110 Why symmetrical? Let = 100. Suppose x = 110. Now suppose x = 90

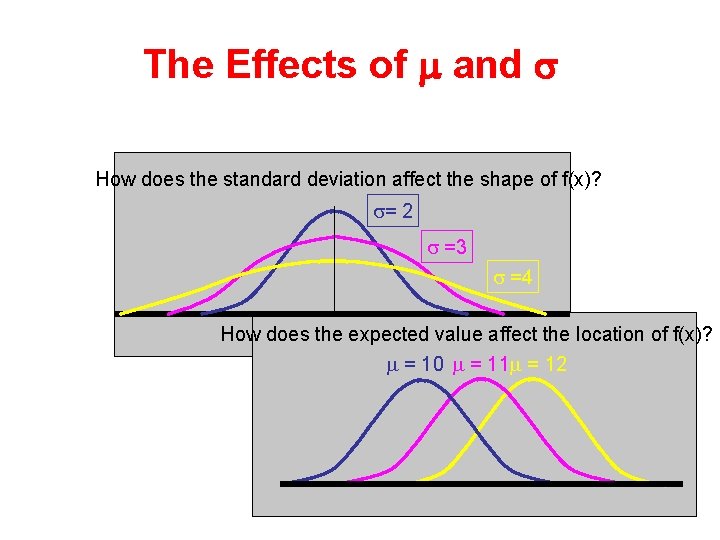
The Effects of m and s How does the standard deviation affect the shape of f(x)? = 2 =3 =4 How does the expected value affect the location of f(x)? = 10 = 11 = 12 10

Finding Normal Probabilities • Two facts help calculate normal probabilities: – The normal distribution is symmetrical. – Any normal distribution can be transformed into a specific normal distribution called… “STANDARD NORMAL DISTRIBUTION” Example The amount of time it takes to assemble a computer is normally distributed, with a mean of 50 minutes and a standard deviation of 10 minutes. What is the probability that a computer is assembled in a time between 45 and 60 minutes? 11

STANDARD NORMAL DISTRIBUTION • NORMAL DISTRIBUTION WITH MEAN 0 AND VARIANCE 1. • IF X~N( , 2), THEN NOTE: Z IS KNOWN AS Z SCORES. • “ ~ “ MEANS “DISTRIBUTED AS” 12

Finding Normal Probabilities • Solution – If X denotes the assembly time of a computer, we seek the probability P(45<X<60). – This probability can be calculated by creating a new normal variable the standard normal variable. Every normal variable with some and , can be transformed into this Z. E(Z) = = 0 Therefore, once probabilities fo are calculated, probabilities of normal variable can be found. V(Z) = 2 = 1 13

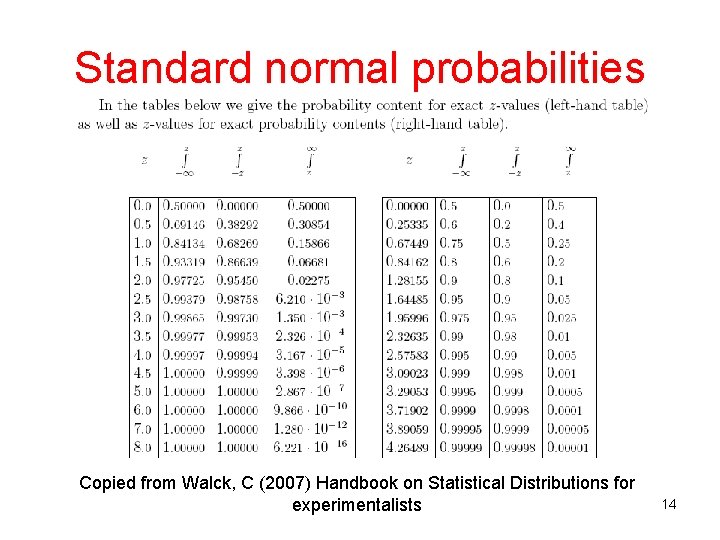
Standard normal probabilities Copied from Walck, C (2007) Handbook on Statistical Distributions for experimentalists 14

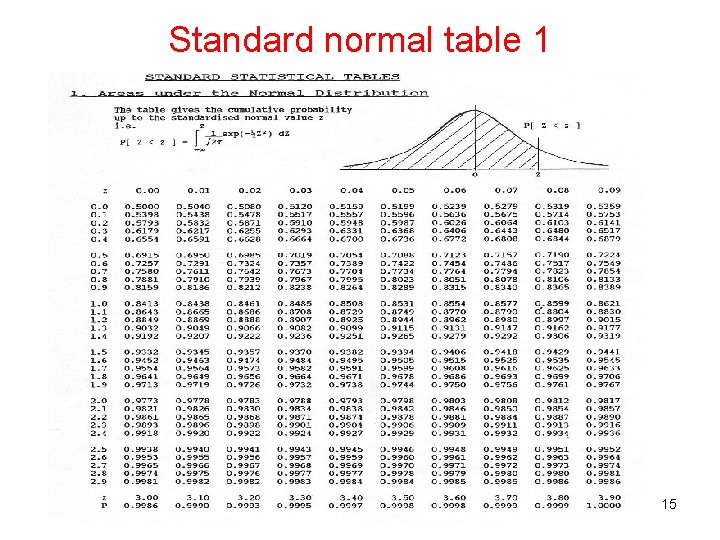
Standard normal table 1 15

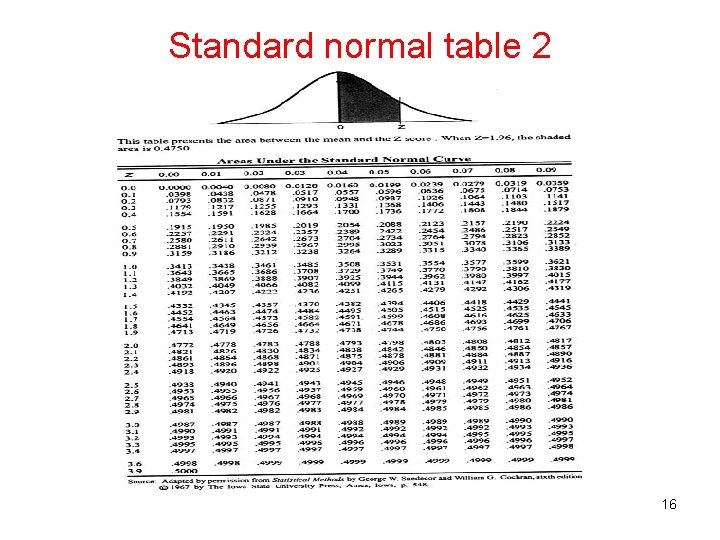
Standard normal table 2 16

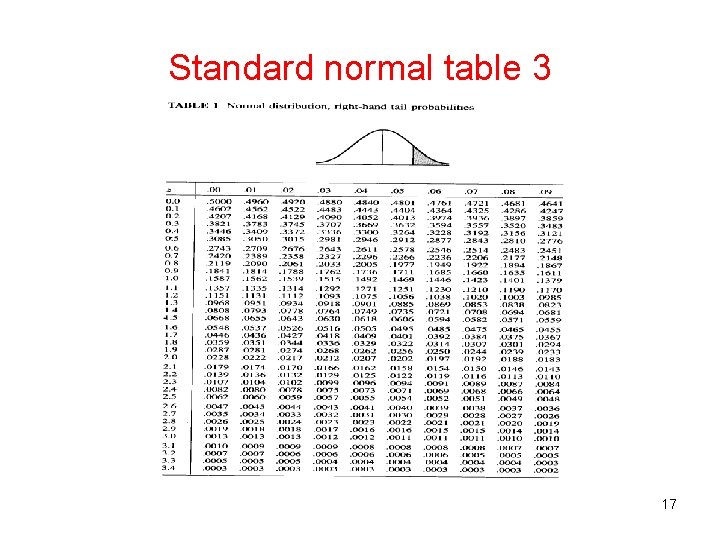
Standard normal table 3 17

Finding Normal Probabilities • Example - continued 45 - 50 P(45<X<60) = P( 10 X < 60 - 50 < 10 ) = P(-0. 5 < Z < 1) To complete the calculation we need to compu the probability under the standard normal distr 18

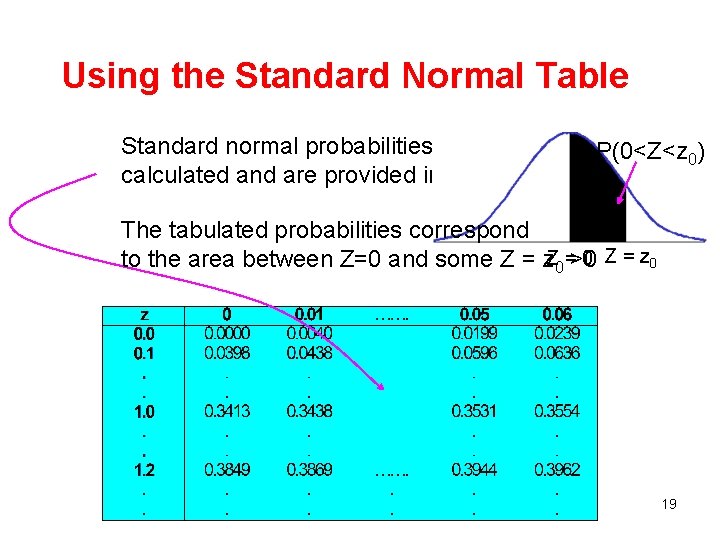
Using the Standard Normal Table Standard normal probabilities have been calculated and are provided in a table. P(0<Z<z 0) The tabulated probabilities correspond 0 Z = z 0 to the area between Z=0 and some Z = z. Z 0 =>0 19

Finding Normal Probabilities • Example - continued 45 - 50 P(45<X<60) = P( 10 X < 60 - 50 < 10 ) = P(-. 5 < Z < 1) We need to find the shaded area z 0 = -. 5 z 0 = 1 20

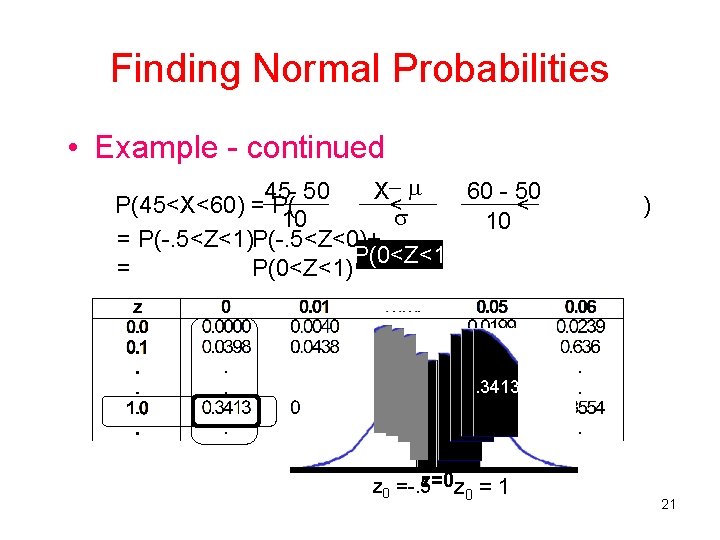
Finding Normal Probabilities • Example - continued 45 - 50 X 60 - 50 P(45<X<60) = P( < < 10 10 = P(-. 5<Z<1)P(-. 5<Z<0)+ P(0<Z<1 = P(0<Z<1) ) . 3413 z=0 z = 1 z 0 =-. 5 0 21

Finding Normal Probabilities • The symmetry of the normal distribution makes it possible to calculate probabilities for negative values of Z using the table as follows: -z 0 0 +z 0 P(-z 0<Z<0) = P(0<Z<z 0) 22

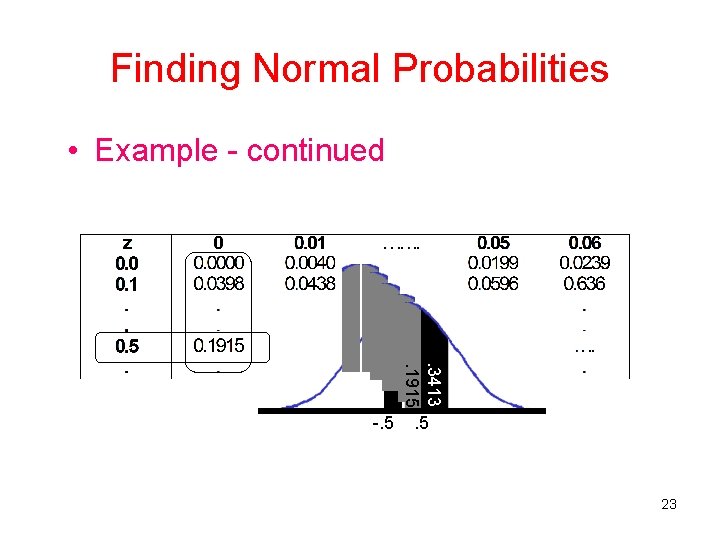
Finding Normal Probabilities • Example - continued . 3413. 1915 -. 5 23

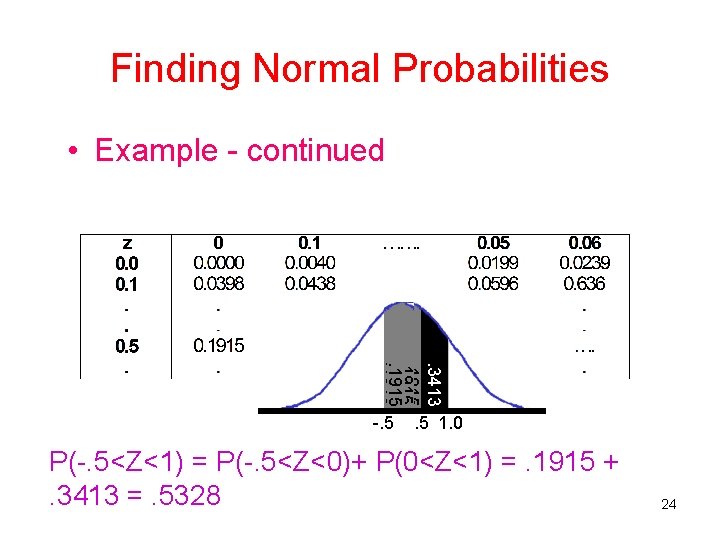
Finding Normal Probabilities • Example - continued . 3413. 1915 -. 5 1. 0 P(-. 5<Z<1) = P(-. 5<Z<0)+ P(0<Z<1) =. 1915 +. 3413 =. 5328 24

Finding Normal Probabilities • Example - continued This table provides probabilities from -∞ to z 0 . 3413 P(Z<-0. 5)=1 -P(Z>-0. 5)=1 -0. 6915=0. 3085 By Symmetry P(Z<0. 5) 25

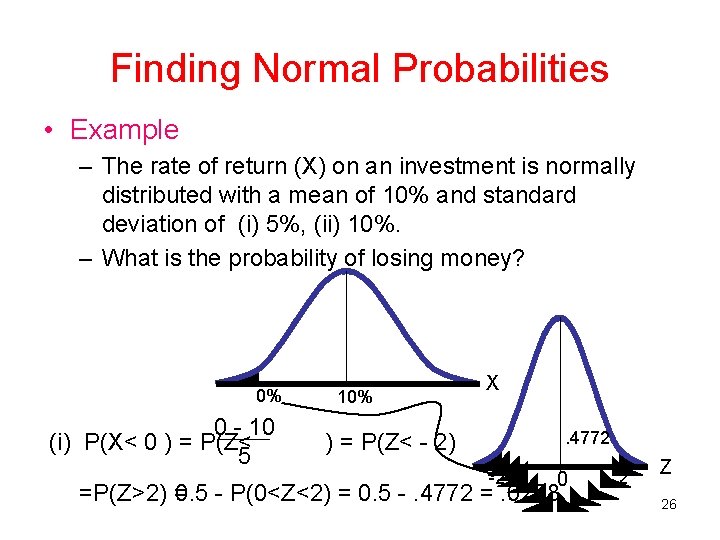
Finding Normal Probabilities • Example – The rate of return (X) on an investment is normally distributed with a mean of 10% and standard deviation of (i) 5%, (ii) 10%. – What is the probability of losing money? 0% 0 - 10 (i) P(X< 0 ) = P(Z< 5 10% X. 4772 ) = P(Z< - 2) -2 0 =P(Z>2) = 0. 5 - P(0<Z<2) = 0. 5 -. 4772 =. 0228 2 Z 26

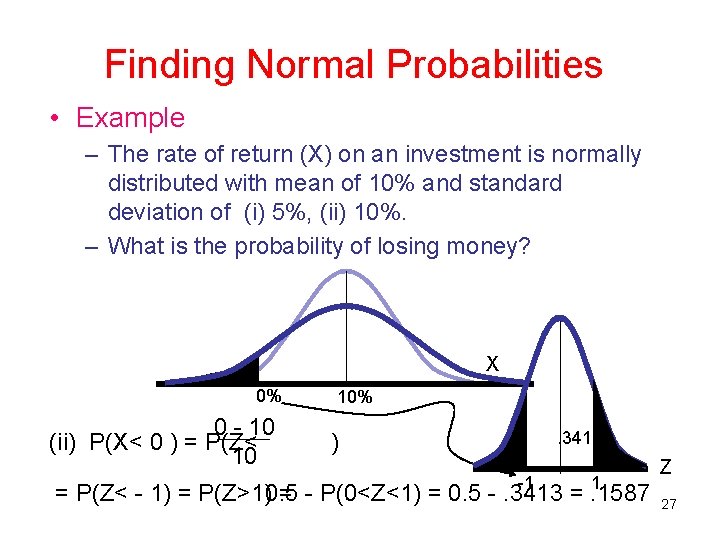
Finding Normal Probabilities • Example – The rate of return (X) on an investment is normally distributed with mean of 10% and standard deviation of (i) 5%, (ii) 10%. – What is the probability of losing money? X 0% 0 - 10 (ii) P(X< 0 ) = P(Z< 10 10%. 3413 ) -1 1 = P(Z< - 1) = P(Z>1)0. 5 = - P(0<Z<1) = 0. 5 -. 3413 =. 1587 Z 27

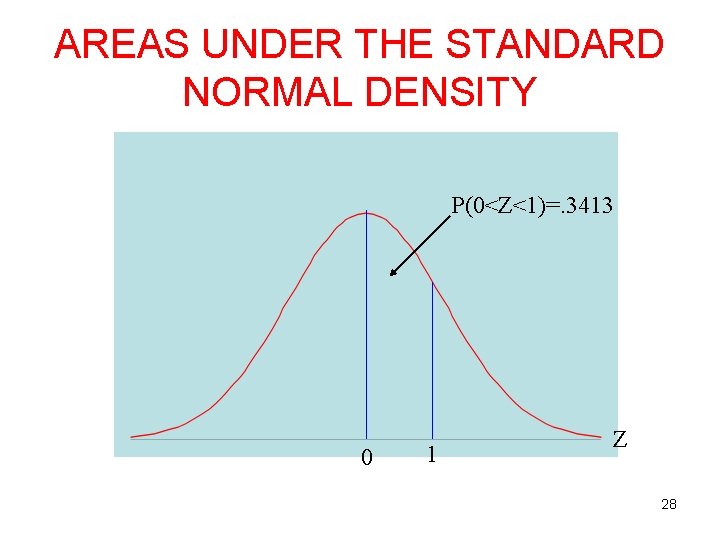
AREAS UNDER THE STANDARD NORMAL DENSITY P(0<Z<1)=. 3413 0 1 Z 28

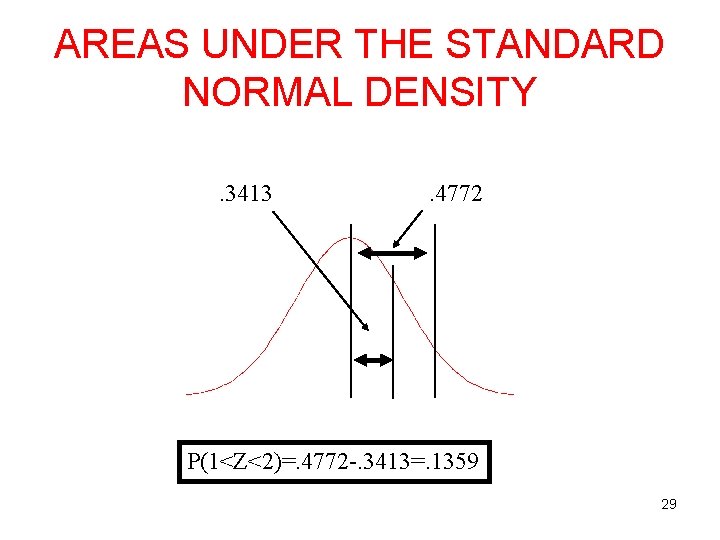
AREAS UNDER THE STANDARD NORMAL DENSITY. 3413 . 4772 P(1<Z<2)=. 4772 -. 3413=. 1359 29

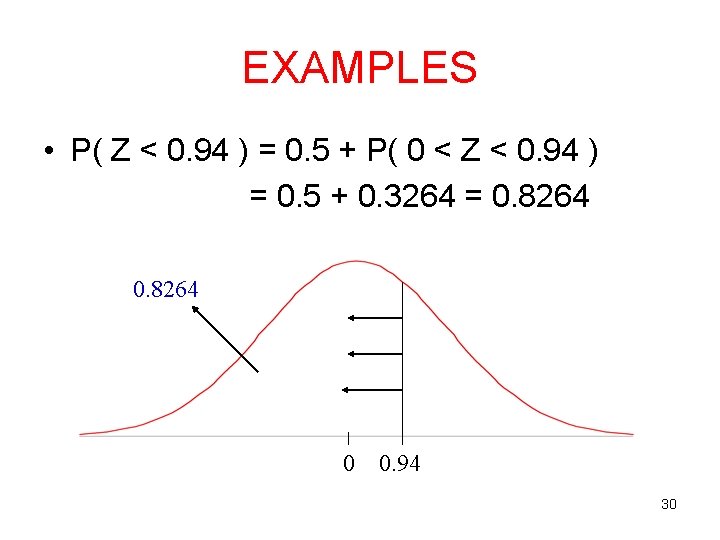
EXAMPLES • P( Z < 0. 94 ) = 0. 5 + P( 0 < Z < 0. 94 ) = 0. 5 + 0. 3264 = 0. 8264 0 0. 94 30

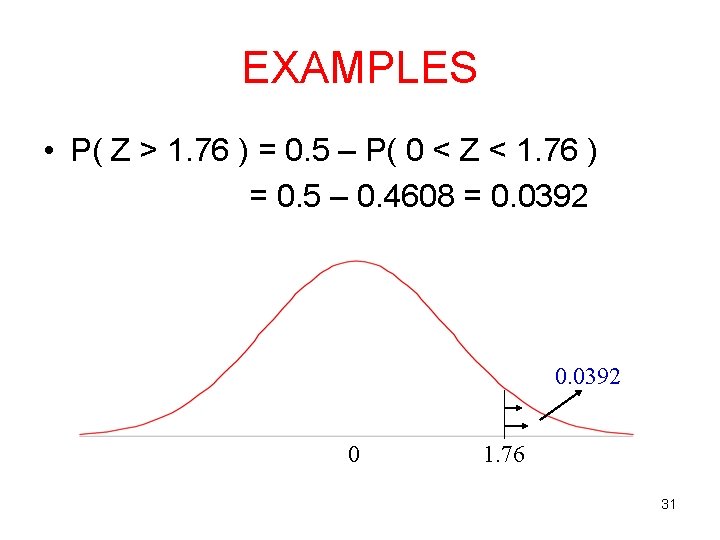
EXAMPLES • P( Z > 1. 76 ) = 0. 5 – P( 0 < Z < 1. 76 ) = 0. 5 – 0. 4608 = 0. 0392 0 1. 76 31

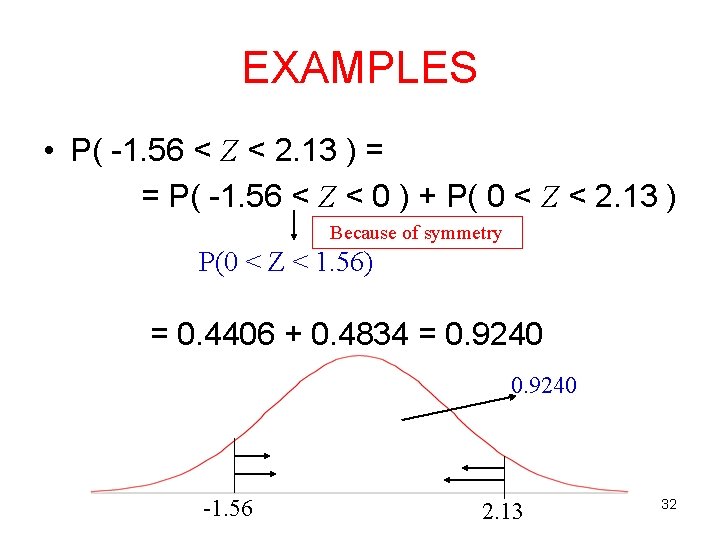
EXAMPLES • P( -1. 56 < Z < 2. 13 ) = = P( -1. 56 < Z < 0 ) + P( 0 < Z < 2. 13 ) Because of symmetry P(0 < Z < 1. 56) = 0. 4406 + 0. 4834 = 0. 9240 -1. 56 2. 13 32

STANDARDIZATION FORMULA • If X~N( , 2), then the standardized value Z of any ‘X-score’ associated with calculating probabilities for the X distribution is: • The standardized value Z of any ‘X-score’ associated with calculating probabilities for the X distribution is: (Converse Formula) 33

Finding Values of Z • Sometimes we need to find the value of Z for a given probability • We use the notation z. A to express a Z value for which P(Z > z. A) = A A z. A 34

PERCENTILE • The pth percentile of a set of measurements is the value for which at most p% of the measurements are less than that value. • 80 th percentile means P( Z < a ) = 0. 80 • If Z ~ N(0, 1) and A is any probability, then P( Z > z. A) = A A z. A 35

Finding Values of Z • Example – Determine z exceeded by 5% of the population – Determine z such that 5% of the population is below • Solution z. 05 is defined as the z value for which the area on its right under the standard normal curve is. 05. 0. 45 0. 05 -Z 0. 05 0 Z 0. 05 1. 645 36

EXAMPLES • Let X be rate of return on a proposed investment. Mean is 0. 30 and standard deviation is 0. 1. a) P(X>. 55)=? Standardization formula b) P(X<. 22)=? c) P(. 25<X<. 35)=? d) 80 th Percentile of X is? Converse Formula e) 30 th Percentile of X is? 37

ANSWERS a) b) c) d) 80 th Percentile of X is e) 30 th Percentile of X is 38

The Normal Approximation to the Binomial Distribution • The normal distribution provides a close approximation to the Binomial distribution when n (number of trials) is large and p (success probability) is close to 0. 5. • The approximation is used only when np 5 and n(1 -p) 5 39

The Normal Approximation to the Binomial Distribution • If the assumptions are satisfied, the Binomial random variable X can be approximated by normal distribution with mean = np and 2 = np(1 -p). • In probability calculations, the continuity correction improves the results. For example, if X is Binomial random variable, then P(X a) ≈ P(X<a+0. 5) P(X a) ≈ P(X>a-0. 5) 40

EXAMPLE • Let X ~ Binomial(25, 0. 6), and want to find P(X ≤ 13). • Exact binomial calculation: • Normal approximation (w/o correction): Y~N(15, 2. 45²) Normal approximation is good, but not great! 41

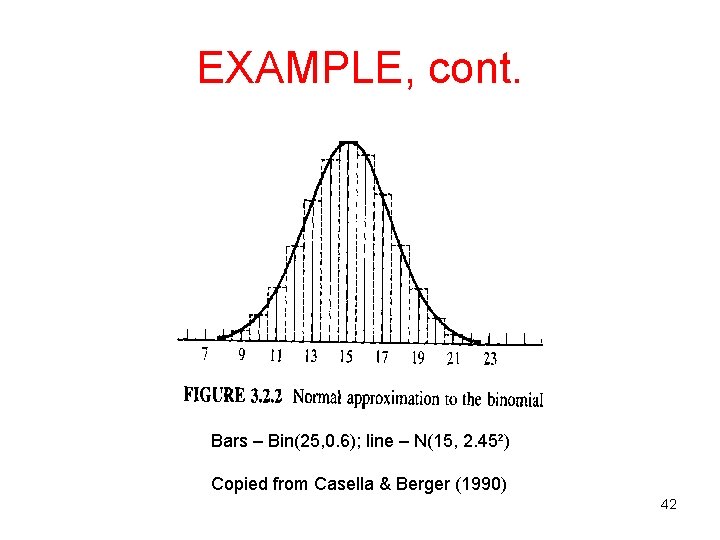
EXAMPLE, cont. Bars – Bin(25, 0. 6); line – N(15, 2. 45²) Copied from Casella & Berger (1990) 42

EXAMPLE, cont. • Normal approximation (w correction): Y~N(15, 2. 45²) Much better approximation to the exact value: 0. 267 43

Exponential Distribution • The exponential distribution can be used to model – the length of time between telephone calls – the length of time between arrivals at a service station – the lifetime of electronic components. • When the number of occurrences of an event follows the Poisson distribution, the time between occurrences follows the exponential distribution. 44

Exponential Distribution A random variable is exponentially distributed if its probability density function is given by f(x) = e- x, x>=0. is a distribution parameter. is the distribution parameter >0). E(X) = V(X) = 2 The cumulative distribution function is F(x) =1 e-x/ , x 0 45

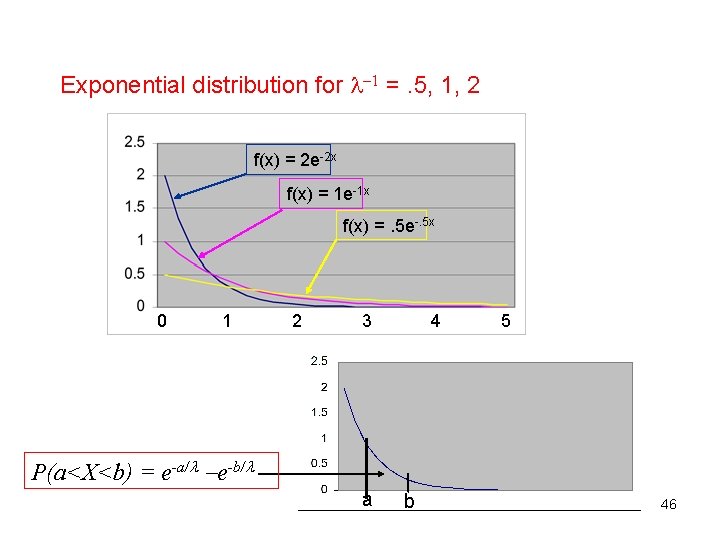
Exponential distribution for 1 =. 5, 1, 2 f(x) = 2 e-2 x f(x) = 1 e-1 x f(x) =. 5 e-. 5 x 0 1 2 3 4 5 P(a<X<b) = e-a/ e-b/ a b 46

Exponential Distribution • Finding exponential probabilities is relatively easy: – P(X < a) = P(X ≤ a)=F(a)=1 – e –a/ – P(X > a) = e–a/ – P(a< X < b) = e – a/ – e – b/ 47

Exponential Distribution • Example – The lifetime of an alkaline battery is exponentially distributed with mean 20 hours. – Find the following probabilities: • The battery will last between 10 and 15 hours. • The battery will last for more than 20 hours. 48

Exponential Distribution • Solution – The mean = standard deviation = = 20 hours. – Let X denote the lifetime. • P(10<X<15) = e-. 05(10) – e-. 05(15) =. 1341 • P(X > 20) = e-. 05(20) =. 3679 49

Exponential Distribution • Example The service rate at a supermarket checkout is 6 customers per hour. – If the service time is exponential, find the following probabilities: • A service is completed in 5 minutes, • A customer leaves the counter more than 10 minutes after arriving • A service is completed between 5 and 8 minutes. 50

Exponential Distribution • Solution – A service rate of 6 per hour = A service rate of. 1 per minute ( 1 =. 1/minute). – P(X < 5) = 1 -e-. lx = 1 – e-. 1(5) =. 3935 – P(X >10) = e-. lx = e-. 1(10) =. 3679 – P(5 < X < 8) = e-. 1(5) – e-. 1(8) =. 1572 51

Exponential Distribution • If pdf of lifetime of fluorescent lamp is exponential with mean 0. 10, find the life for 95% reliability? The reliability function = R(t) = 1 F(t) = e-t/ R(t) = 0. 95 t = ? 52

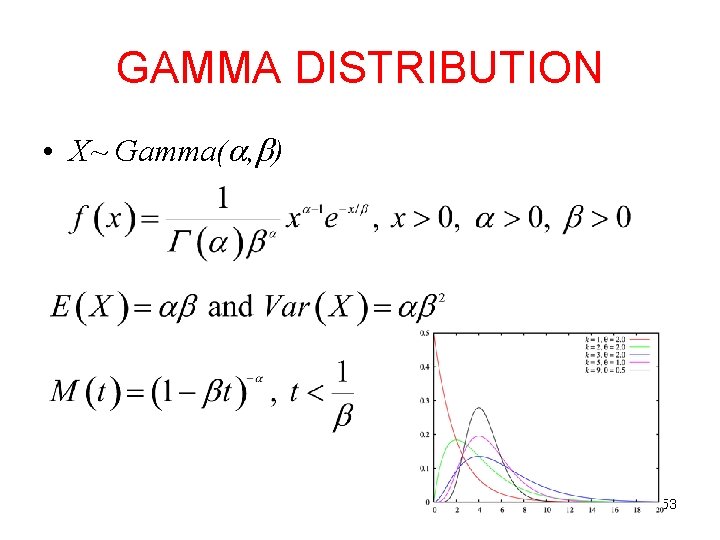
GAMMA DISTRIBUTION • X~ Gamma( , ) 53

GAMMA DISTRIBUTION • Gamma Function: where is a positive integer. Properties: 54

GAMMA DISTRIBUTION since the last integral is the expectation of a Gamma distribution with parameters alpha and 1. 55

GAMMA DISTRIBUTION • Let X 1, X 2, …, Xn be independent rvs with Xi~Gamma( i, ). Then, • Let X be an rv with X~Gamma( , ). Then, • Let X 1, X 2, …, Xn be a random sample with Xi~Gamma( , ). Then, 56

GAMMA DISTRIBUTION • Special cases: Suppose X~Gamma(α, β) – If α=1, then X~ Exponential(β) – If α=p/2, β=2, then X~ 2 (p) (will come back in a min. ) – If Y=1/X, then Y ~ inverted gamma. • Gamma approximates to Normal distribution on the limit as alpha goes to infinity. 57

Integral tricks • Recall: h(t) is an odd function if h(-t)=-h(t); It is an even function if h(-t)=h(t). • Ex: h(x)=x exp{-x²/2} odd; h(x)= exp{-x²/2 -x} neither odd nor even • odd function =0 • even function = 2* even function 58

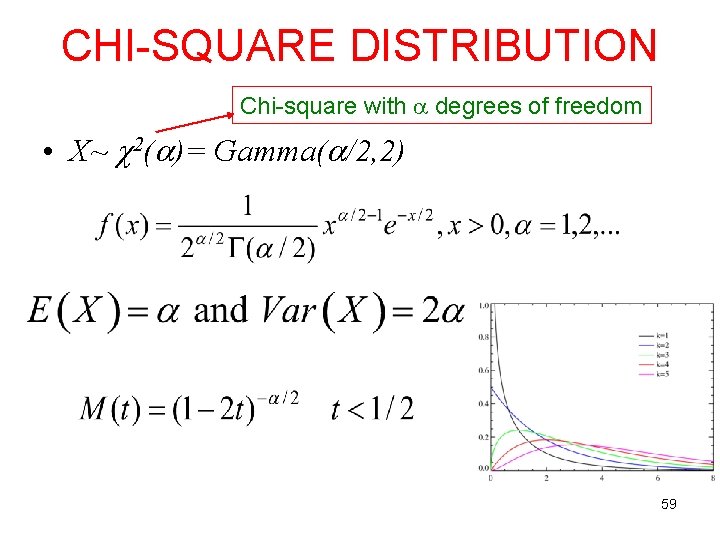
CHI-SQUARE DISTRIBUTION Chi-square with degrees of freedom • X~ 2( )= Gamma( /2, 2) 59

DEGREES OF FREEDOM • In statistics, the phrase degrees of freedom is used to describe the number of values in the final calculation of a statistic that are free to vary. • The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom (df). • How many components need to be known before the vector is fully determined? 60

CHI-SQUARE DISTRIBUTION • Chi-square (2) ≡ Exponential (2) 61

CHI-SQUARE DISTRIBUTION • If rv X has Gamma( , ) distribution, then Y=2 X/ has Gamma( , 2) distribution. If 2 is positive integer, then Y has distribution. • Let X be an rv with X~N(0, 1). Then, • Let X 1, X 2, …, Xn be a r. s. with Xi~N(0, 1). Then, 62

BETA DISTRIBUTION • The Beta family of distributions is a continuous family on (0, 1) and often used to model proportions. where 63

WEIBULL DISTRIBUTION • To model the failure time data or hazard functions. • Hazard function: Rate of change in prob that subject survives a little past time t, given that subject survives upto time t. • If X~Exp( ), then Y=X 1/ has Weibull( , ) distribution. 64

CAUCHY DISTRIBUTION • It is a symmetric and bell-shaped distribution on ( , ) with pdf , the mean does not exist. Since • The mgf does not exist. • measures the center of the distribution and it is the median. • If X and Y have N(0, 1) distribution, then Z=X/Y has a Cauchy distribution with =0 and σ=1. 65

CAUCHY DISTRIBUTION • When studying hypothesis tests that assume normality, seeing how the tests perform on data from a Cauchy distribution is a good indicator of how sensitive the tests are to heavy-tail departures from normality. • Likewise, it is a good check for robust techniques that are designed to work well under a wide variety of distributional assumptions. 66

LOG-NORMAL DISTRIBUTION • An rv X is said to have the lognormal distribution, with parameters µ and 2, if Y=ln(X) has the N(µ, 2) distribution. • The lognormal distribution is used to model continuous random quantities when the distribution is believed to be skewed, such as certain income and lifetime variables. 67

STUDENT’S T DISTRIBUTION • This distribution will arise in the study of population mean when the underlying distribution is normal. • Let Z be a standard normal rv and let U be a chi-square distributed rv independent of Z, with degrees of freedom. Then, When n , X N(0, 1). 68

F DISTRIBUTION • Let U and V be independent rvs with chisquare distributions with 1 and 2 degrees of freedom. Then, 69

MULTIVARIATE DISTRIBUTIONS 70

BIVARIATE NORMAL DISTRIBUTION • A pair of continuous rvs X and Y is said to have a bivariate normal distribution if it has a joint pdf of the form 71

BIVARIATE NORMAL DISTRIBUTION If , then and is the correlation coefficient btw X and Y. 1. Conditional on X=x, 2. Conditional on Y=y, 72

Mixture of distributions • Let f 1(y) and f 2(y) be density functions, and let a be a constant such that 0≤ a ≤ 1. Consider the function f(y)=a f 1(y) + (1 -a) f 2(y) Such a density function is often called a mixture distribution. Here are some examples of real life applications for such distributions. 73

Mixture of distributions • Example 1: Financial returns often behave differently in normal situations and during crisis times. A mixture of two normal distributions with different means and variances can be assumed for returns, one for the returns during normal situations, and another for during crises. 74

Mixture of distributions • Example 2: The prices of houses in a particular neighborhood will tend to be similar, while prices in a different neighborhood may be extremely different. For instance, if we are to collect prices in both Cukurambar and Sincan, we will need a mixture of two distributions to describe these prices. 75

Mixture of distributions • Note that f(y) is a valid density function. • Suppose that Y 1 is a random variable with density function f 1(y), and E(Y 1)=μ 1 and Var(Y 1)=. Similarly, suppose that Y 2 is a random variable with density function f 2(y), and E(Y 2)=μ 2 and Var(Y 2)=. Assume that Y is random variable whose density is a mixture of the densities corresponding to Y 1 and Y 2. i) It can be shown that E(Y)= a μ 1 + (1 -a) μ 2 ii) It can be shown that Var(Y)= a + (1 -a) + a(1 -a) (μ 1 - μ 2)2 76

Problems 1. Mensa (from the Latin word for “mind”) is an international society devoted to intellectual pursuits. Any person who has an IQ in the upper 2% of the general population is eligible to join. If we assume that IQs are normally distributed with μ = 100 and σ = 16, what is the lowest IQ that will qualify a person for membership? 77

Solution 78

Problems 2. Suppose that numerical grades in a statistics class are values of a r. v. X which is Normally distributed with mean μ = 65 and standard deviation 15. Suppose that letter grades are assigned according to the following rule: student receives an A if X ≥ 85; B if 70 ≤ X < 85; C if 55 ≤ X < 70; D if 45 ≤ X < 55; and F if X ≤ 45. If a student is chosen at random from this class, calculate the probability that the student will earn i) A; ii) B; iii) F. 79

Solution 80

Problems 3. Economic conditions cause fluctuations in the prices of raw commodities as well as in finished products. Let X denote the price paid for a barrel of crude oil by the initial carrier, and let Y denote the price paid by the refinery purchasing the product from the carrier. Assume that the joint density for (X, Y) is given by f(x, y)=c 20< x < y < 40 81

Problems a) Find the value of c that makes this a joint density for a two-dimensional random variable. b) Find the probability that the carrier will pay at least $25 per barrel and the refinery will pay at most $30 per barrel for the oil. c) Find the probability that the price paid by the refinery exceeds that of the carrier by at least $10 per barrel. 82

Problems d) Are X and Y independent? Explain. e) Find E(Y-X). Interpret this expectation in a practical sense. 83

Solution 84

Solution 85

Solution d) e) 86