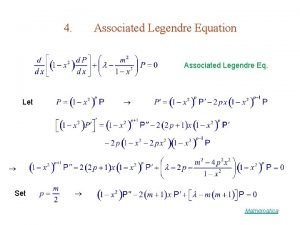Hamiltonian Formalism Legendre transformations Legendre transformation AdrienMarie Legendre

Hamiltonian Formalism

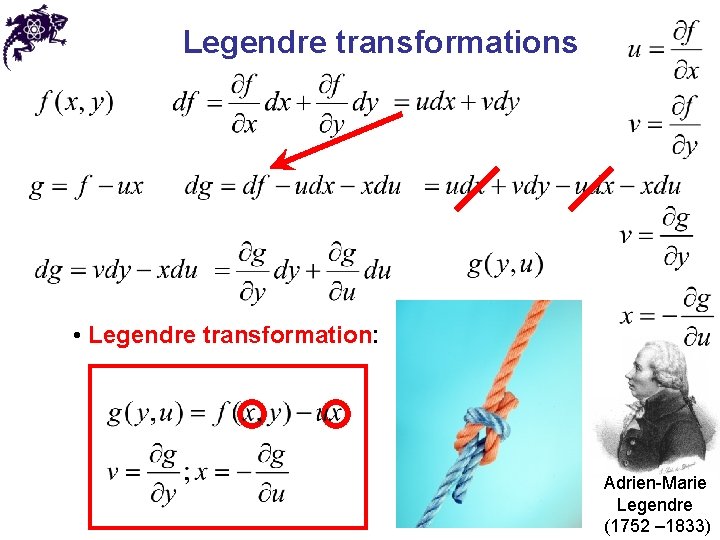
Legendre transformations • Legendre transformation: Adrien-Marie Legendre (1752 – 1833)

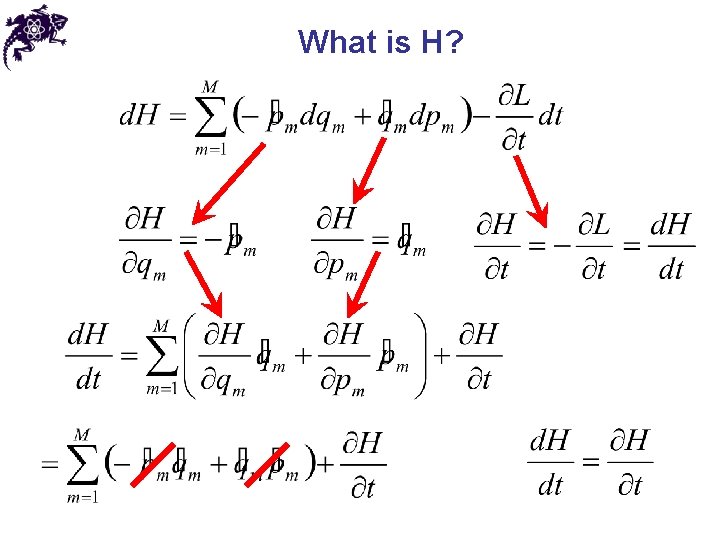
What is H? • Conjugate momentum • Then • So

What is H?

What is H?

What is H? • If • Then • Kinetic energy • In generalized coordinates

What is H? • For scleronomous generalized coordinates • Then • If

What is H? • For scleronomous generalized coordinates, H is a total mechanical energy of the system (even if H depends explicitly on time) • If H does not depend explicitly on time, it is a constant of motion (even if is not a total mechanical energy) • In all other cases, H is neither a total mechanical energy, nor a constant of motion

Hamilton’s equations • Hamiltonian: • Hamilton’s equations of motion: Sir William Rowan Hamilton (1805 – 1865)

Hamiltonian formalism • For a system with M degrees of freedom, we have 2 M independent variables q and p: 2 M-dimensional phase space (vs. configuration space in Lagrangian formalism) • Instead of M second-order differential equations in the Lagrangian formalism we work with 2 M first-order differential equations in the Hamiltonian formalism • Hamiltonian approach works best for closed holonomic systems • Hamiltonian approach is particularly useful in quantum mechanics, statistical physics, nonlinear physics, perturbation theory

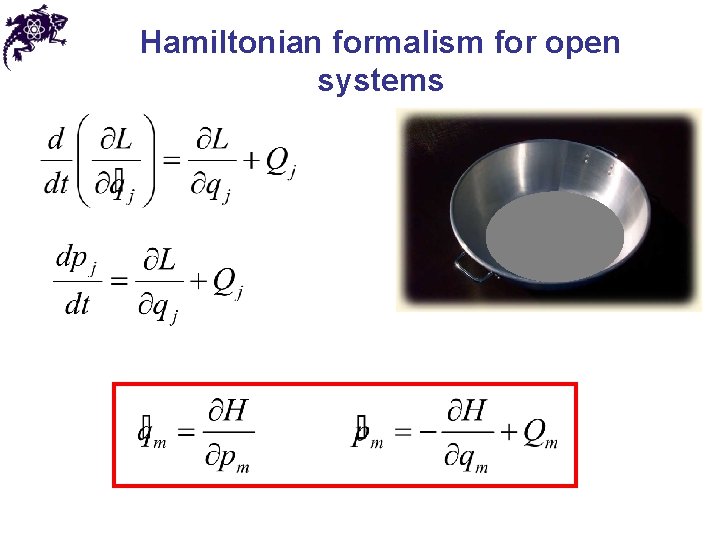
Hamiltonian formalism for open systems

Hamilton’s equations in symplectic notation • Construct a column matrix (vector) with 2 M elements • Then • Construct a 2 Mx 2 M square matrix as follows:

Hamilton’s equations in symplectic notation • Then the equations of motion will look compact in the symplectic (matrix) notation: • Example (M = 2):

Lagrangian to Hamiltonian • Obtain conjugate momenta from a Lagrangian • Write a Hamiltonian • Obtain from • Plug into the Hamiltonian to make it a function of coordinates, momenta, and time

Lagrangian to Hamiltonian • For a Lagrangian quadratic in generalized velocities • Write a symplectic notation: • Then a Hamiltonian • Conjugate momenta

Lagrangian to Hamiltonian • Inverting this equation • Then a Hamiltonian

Example: electromagnetism

Example: electromagnetism

Hamilton’s equations from the variational principle • Action functional : • Variations in the phase space :

Hamilton’s equations from the variational principle • Integrating by parts

Hamilton’s equations from the variational principle • For arbitrary independent variations

Conservation laws • If a Hamiltonian does not depend on a certain coordinate explicitly (cyclic), the corresponding conjugate momentum is a constant of motion • If a Hamiltonian does not depend on a certain conjugate momentum explicitly (cyclic), the corresponding coordinate is a constant of motion • If a Hamiltonian does not depend on time explicitly, this Hamiltonian is a constant of motion

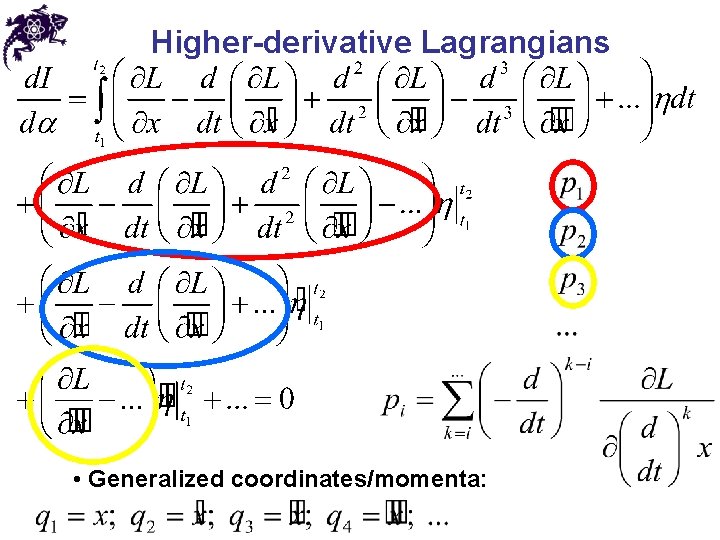
Higher-derivative Lagrangians • Let us recall: • Lagrangians with i > 1 occur in many systems and theories: 1. Non-relativistic classical radiating charged particle (see Jackson) 2. Dirac’s relativistic generalization of that 3. Nonlinear dynamics 4. Cosmology 5. String theory 6. Etc.

Higher-derivative Lagrangians • For simplicity, consider a 1 D case: • Variation Mikhail Vasilievich Ostrogradsky (1801 - 1862)

Higher-derivative Lagrangians

Higher-derivative Lagrangians

Higher-derivative Lagrangians • Generalized coordinates/momenta:

Higher-derivative Lagrangians • Euler-Lagrange equations: • We have formulated a ‘higher-order’ Lagrangian formalism • What kind of behavior does it produce?

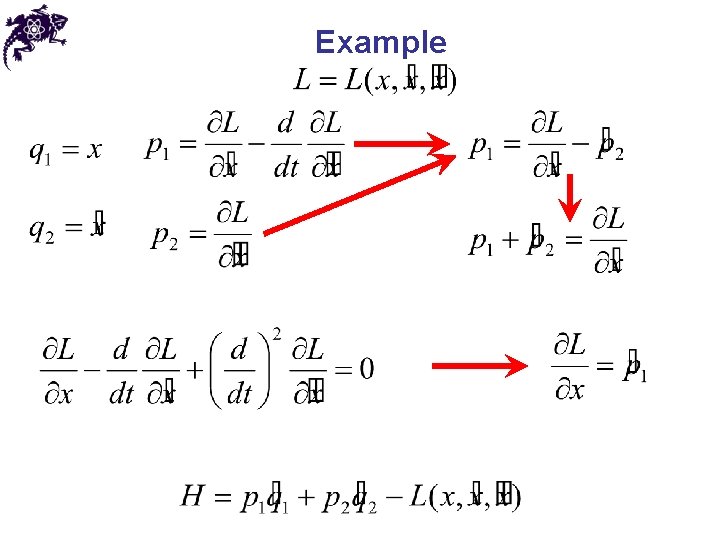
Example

Example

Example • H is conserved and it generates evolution – it is a Hamiltonian! • Hamiltonian linear in momentum? !? !? ! • No low boundary on the total energy – lack of ground state!!! • Produces ‘runaway’ solutions: the system becomes highly unstable - collapse and explosion at the same time

‘Runaway’ solutions • Unrestricted low boundary of the total energy produces instabilities • Additionally, we generate new degrees of freedom, which require introduction of additional (originally unknown) initial conditions for them • These problems are solved by means of introduction of constraints • Constraints restrict unstable behavior and eliminate unnecessary new degrees of freedom

Canonical transformations • Recall gauge invariance (leaves the evolution of the system unchanged): • Let’s combine gauge invariance with Legendre transformation: • K – is the new Hamiltonian (‘Kamiltonian’ ) • K may be functionally different from H 9. 1

Canonical transformations • Multiplying by the time differential: • So 9. 1

Generating functions • Such functions are called generating functions of canonical transformations • They are functions of both the old and the new canonical variables, so establish a link between the two sets • Legendre transformations may yield a variety of other generating functions 9. 1

Generating functions • We have three additional choices: • Canonical transformations may also be produced by a mixture of the four generating functions 9. 1

An example of a canonical transformation • Generalized coordinates are indistinguishable from their conjugate momenta, and the nomenclature for them is arbitrary • Bottom-line: generalized coordinates and their conjugate momenta should be treated equally in the phase space 9. 2

Criterion for canonical transformations • How to make sure this transformation is canonical? • On the other hand • If • Then 9. 4

Criterion for canonical transformations • Similarly, • If • Then 9. 4

Criterion for canonical transformations • So, • If 9. 4

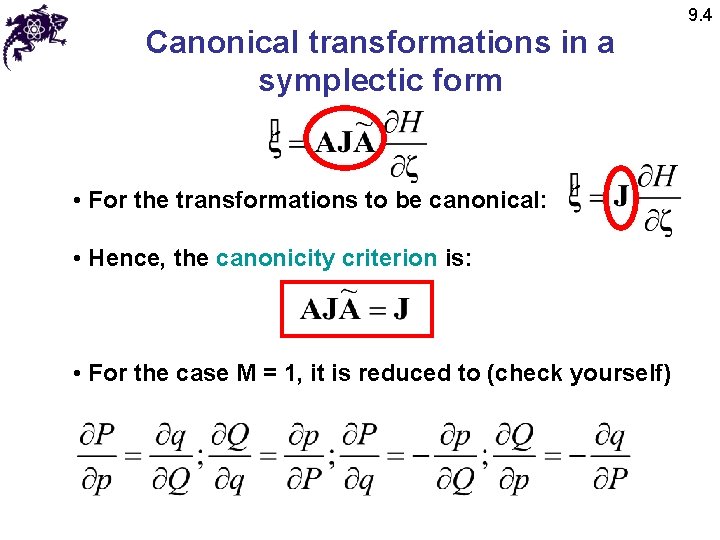
Canonical transformations in a symplectic form • After transformation • On the other hand 9. 4

Canonical transformations in a symplectic form • For the transformations to be canonical: • Hence, the canonicity criterion is: • For the case M = 1, it is reduced to (check yourself) 9. 4

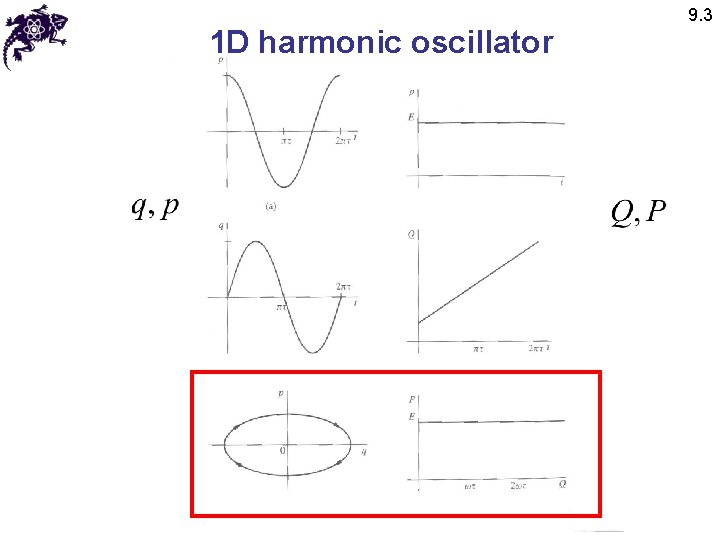
1 D harmonic oscillator • Let us find a conserved canonical momentum • Generating function 9. 3

1 D harmonic oscillator • Nonlinear partial differential equation for F • Let’s try to separate variables • Let’s try 9. 3

1 D harmonic oscillator • We found a generating function! 9. 3

1 D harmonic oscillator 9. 3

1 D harmonic oscillator 9. 3

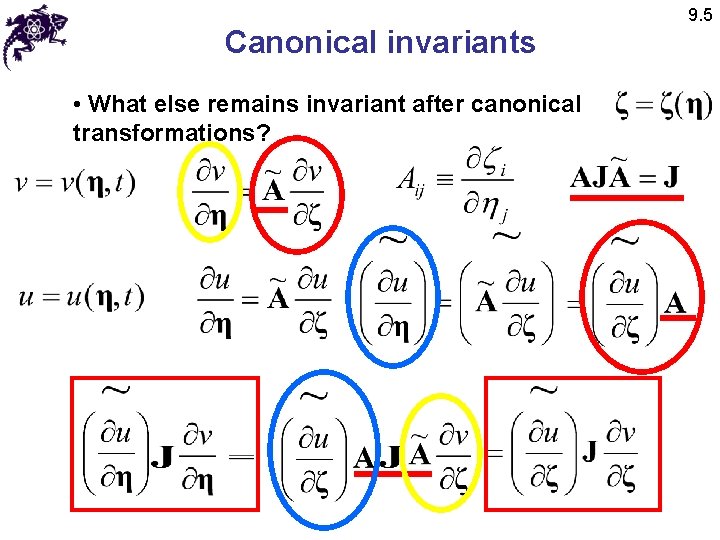
Canonical invariants • What remains invariant after a canonical transformation? • Matrix A is a Jacobian of a space transformation • From calculus, for elementary volumes: • Transformation is canonical if 9. 5

Canonical invariants • For a volume in the phase space • Magnitude of volume in the phase space is invariant with respect to canonical transformations: 9. 5

Canonical invariants • What else remains invariant after canonical transformations? 9. 5

Canonical invariants • For M = 1 • For many variables 9. 5

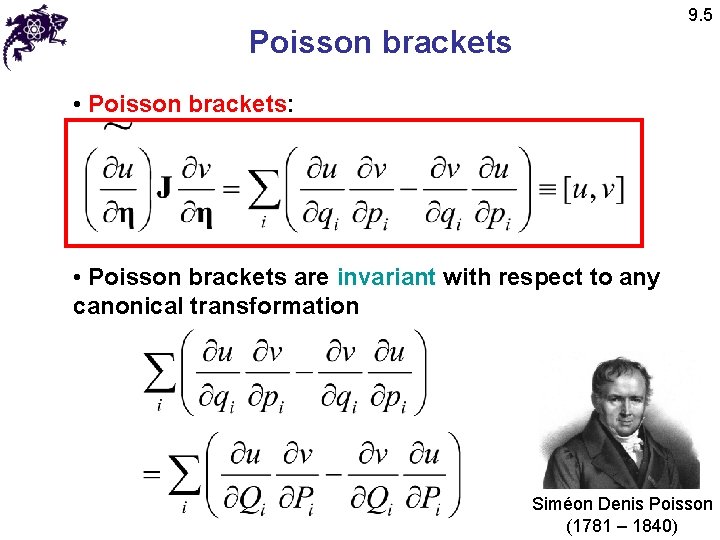
9. 5 Poisson brackets • Poisson brackets: • Poisson brackets are invariant with respect to any canonical transformation Siméon Denis Poisson (1781 – 1840)

Poisson brackets • Properties of Poisson brackets : 9. 5

Poisson brackets • In matrix element notation: • In quantum mechanics, for the commutators of coordinate and momentum operators: 9. 5

Poisson brackets and equations of motion 9. 6

9. 6 Poisson brackets and conservation laws • If u is a constant of motion • If u has no explicit time dependence • In quantum mechanics, conserved quantities commute with the Hamiltonian

9. 6 Poisson brackets and conservation laws • If u and v are constants of motion with no explicit time dependence • For Poisson brackets: • If we know at least two constants of motion, we can obtain further constants of motion

Infinitesimal canonical transformations • Let us consider a canonical transformation with the following generating function (ε – small parameter): • Then 9. 4

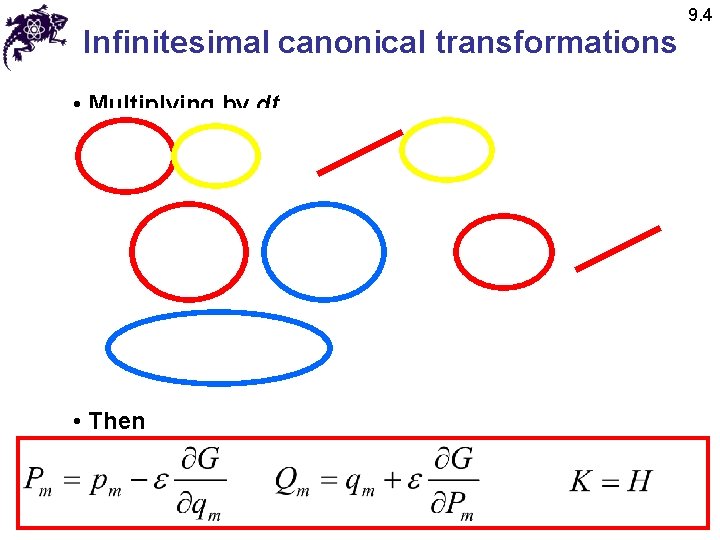
Infinitesimal canonical transformations • Multiplying by dt • Then 9. 4

Infinitesimal canonical transformations • Infinitesimal canonical transformations: • In symplectic notation: 9. 4

Evolution generation • Motion of the system in time interval dt can be described as an infinitesimal transformation generated by the Hamiltonian • The system motion in a finite time interval is a succession of infinitesimal transformations, equivalent to a single finite canonical transformation • Evolution of the system is a canonical transformation!!! 9. 6

Application to statistical mechanics • In statistical mechanics we deal with huge numbers of particles • Instead of describing each particle separately, we describe a given state of the system • Each state of the system represents a point in the phase space • We cannot determine the initial conditions exactly • Instead, we study a certain phase volume – ensemble – as it evolves in time 9. 9

Application to statistical mechanics • Ensemble can be described by its density – a number of representative points in a given phase volume • The number of representative points does not change • Ensemble evolution can be thought as a canonical transformation generated by the Hamiltonian • Volume of a phase space is a constant for a canonical transformation 9. 9

Application to statistical mechanics • Ensemble is evolving so its density is evolving too • On the other hand • Liouville’s theorem • In statistical equilibrium Joseph Liouville (1809 -1882) 9. 9

Hamilton–Jacobi theory 10. 1 • We can look for the following canonical transformation, relating the constant (e. g. initial) values of the variables with the current ones: • The reverse transformations will give us a complete solution

Hamilton–Jacobi theory • Let us assume that the Kamiltonian is identically zero • Then • Choosing the following generating function • Then, for such canonical transformation: 10. 1

Hamilton–Jacobi theory • Hamilton–Jacobi equation • Conventionally: 10. 1 Sir William Rowan Hamilton (1805 – 1865) Hamilton’s principal function • Partial differential equation • First order differential equation • Number of variables: M + 1 Karl Gustav Jacobi (1804 – 1851)

Hamilton–Jacobi theory 10. 1 • Suppose the solution exists, so it will produce M + 1 constants of integration: • One constant is evident: • We chose those M constants to be the new momenta • While the old momenta

Hamilton–Jacobi theory 10. 1 • We relate the constants with the initial values of our old variables: • The new coordinates are defined as: • Inverting those formulas we solve our problem

Have we met before? • Remember action? 10. 1

Hamilton’s characteristic function • When the Hamiltonian does not depend on time explicitly • Generating function (Hamilton’s characteristic function) 10. 1

Hamilton’s characteristic function 10. 3 • Now we require: • So: • Detailed comparison of Hamilton’s characteristic vs. Hamilton’s principal is given in a textbook (10. 3)

Hamilton’s characteristic function • What is the relationship between S and W ? • One of possible relationships (the most conventional): 10. 3

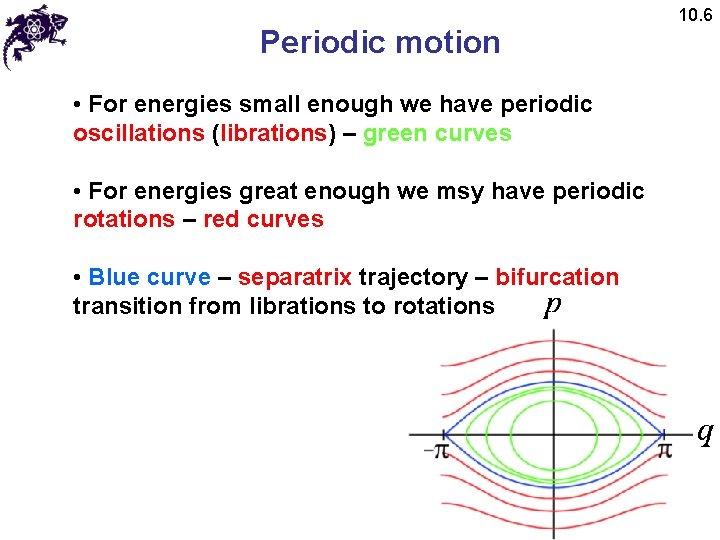
Periodic motion • For energies small enough we have periodic oscillations (librations) – green curves • For energies great enough we msy have periodic rotations – red curves • Blue curve – separatrix trajectory – bifurcation transition from librations to rotations 10. 6

Action-angle variables • For either type of periodic motion let us introduce a new variable – action variable (don’t confuse with action!): • A generalized coordinate conjugate to action variable is the angle variable: • The equation of motion for the angle variable: 10. 6

Action-angle variables • In a compete cycle • This is a frequency of the periodic motion 10. 6

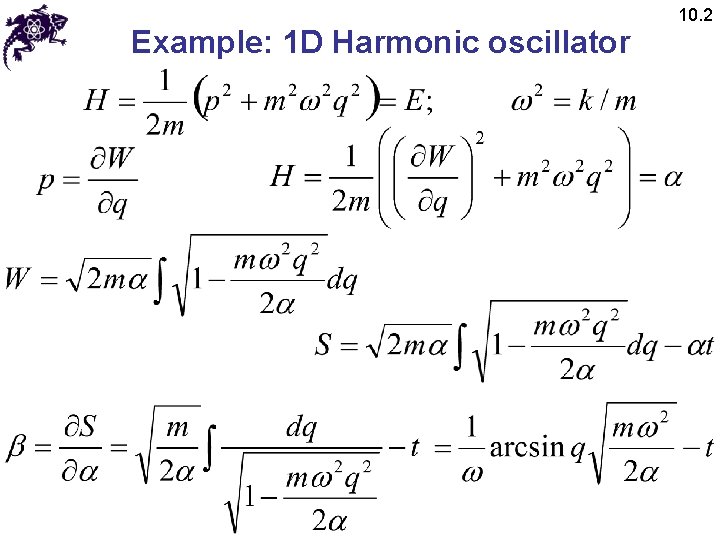
Example: 1 D Harmonic oscillator 10. 2

Example: 1 D Harmonic oscillator 10. 2

10. 6 Action-angle variables for 1 D harmonic oscillator • Therefore, for the frequency:

10. 4 Separation of variables in the Hamilton. Jacobi equation • Sometimes, the principal function can be successfully separated in the following way: • For the Hamiltonian without an explicit time dependence: • Functions Hi may or may not be Hamiltonians