CHAPTER 16 Planar Kinematics of a Rigid Body

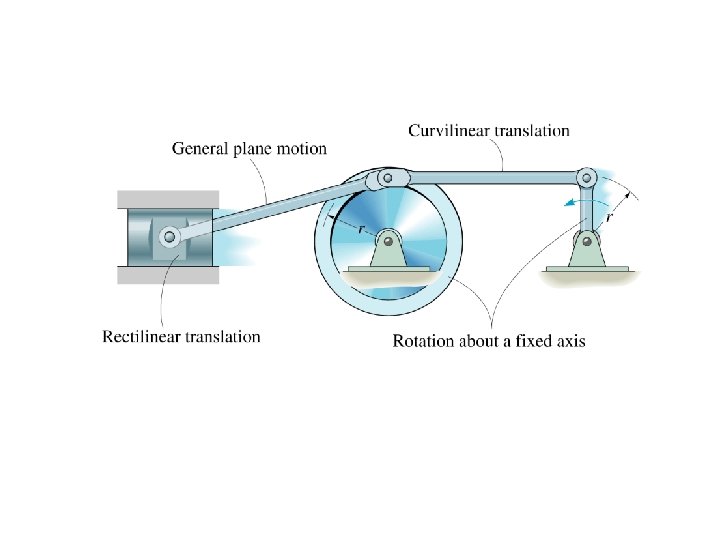
CHAPTER 16 Planar Kinematics of a Rigid Body Important for the design of gears, cam, and mechanisms used for many mechanical operation. When all the particles of a rigid body move along paths which are equidistant from a fixed plane, the body is said to undergo planar motion.

Objectives 1. To classify various types of rigid-body planar motion 2. To investigate rigid-body translation and show to analyze motion about a fixed axis. 3. To study planar motion using an absolute motion analysis.

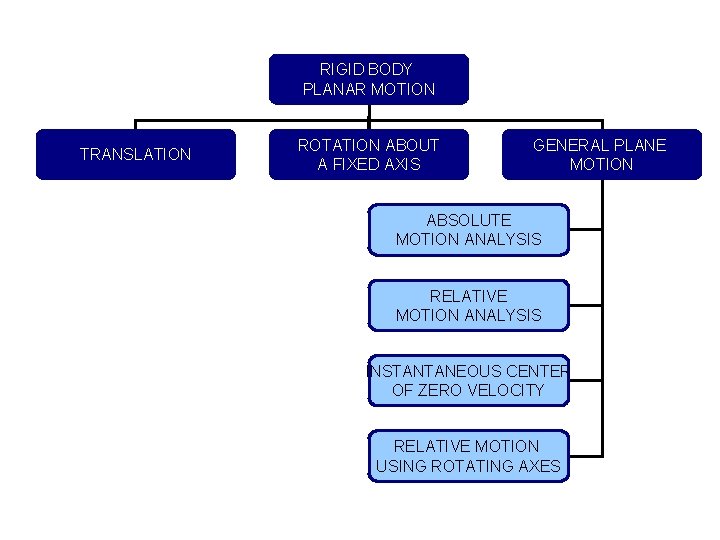
RIGID BODY PLANAR MOTION TRANSLATION ROTATION ABOUT A FIXED AXIS GENERAL PLANE MOTION ABSOLUTE MOTION ANALYSIS RELATIVE MOTION ANALYSIS INSTANTANEOUS CENTER OF ZERO VELOCITY RELATIVE MOTION USING ROTATING AXES

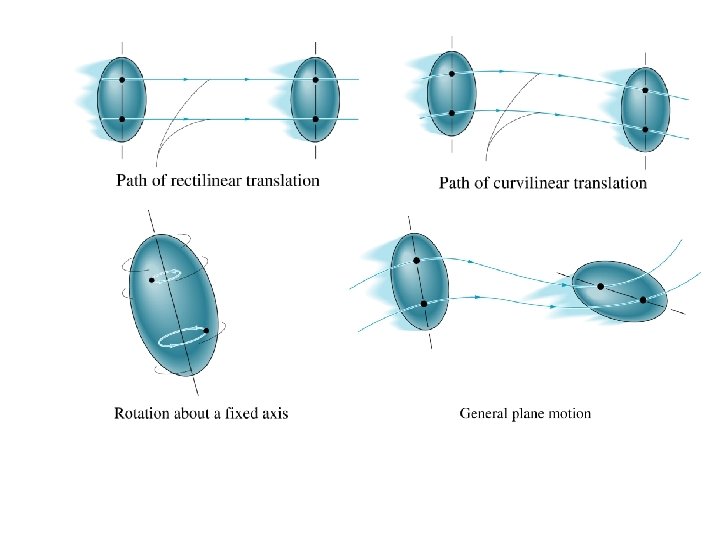
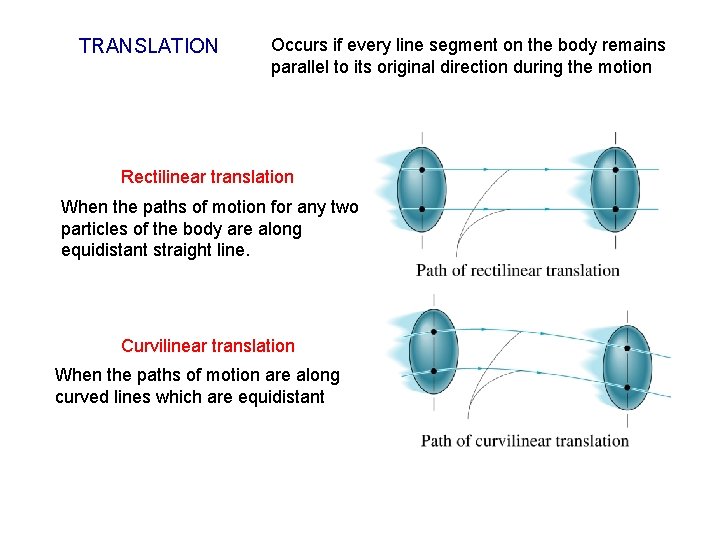
TRANSLATION Occurs if every line segment on the body remains parallel to its original direction during the motion Rectilinear translation When the paths of motion for any two particles of the body are along equidistant straight line. Curvilinear translation When the paths of motion are along curved lines which are equidistant

Passengers on this amusement ride are subjected to curvilinear translation since the vehicle moves in a circular path but always remains upright.

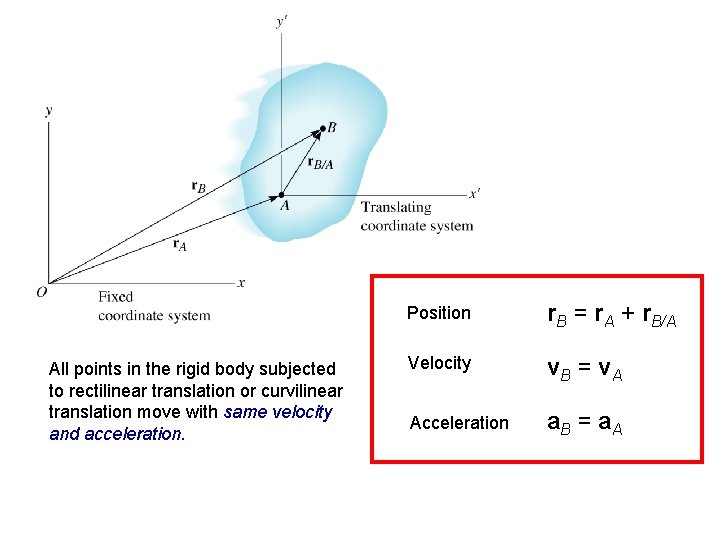
All points in the rigid body subjected to rectilinear translation or curvilinear translation move with same velocity and acceleration. Position r. B = r. A + r. B/A Velocity v. B = v. A Acceleration a. B = a. A

Rotation about a Fixed Axis When a rigid body rotates about a fixed axis, all the particles of the body, (except those which lie on the axis of rotation) move along a circular paths. All line segments in the body undergo the same angular displacement, angular velocity, and angular acceleration.

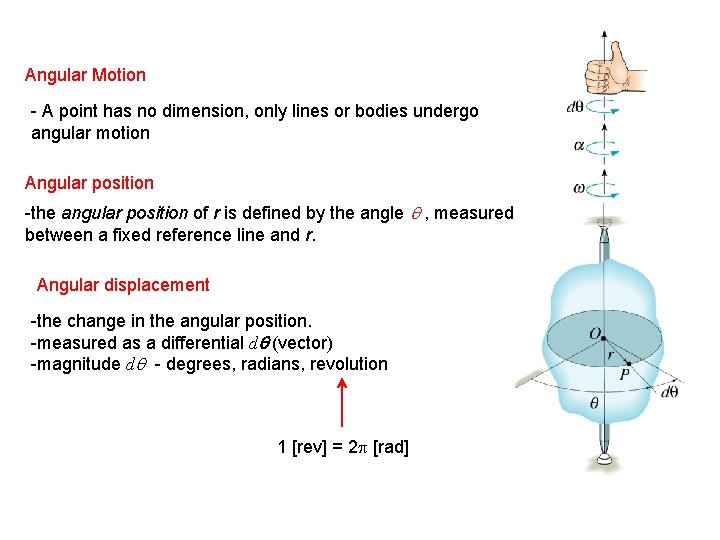
Angular Motion - A point has no dimension, only lines or bodies undergo angular motion Angular position -the angular position of r is defined by the angle q , measured between a fixed reference line and r. Angular displacement -the change in the angular position. -measured as a differential dq (vector) -magnitude dq - degrees, radians, revolution 1 [rev] = 2 p [rad]

Angular velocity, w - Time rate of change in the angular position [rad/s]

Angular acceleration, a - Time rate of change of the angular velocity Constant angular acceleration

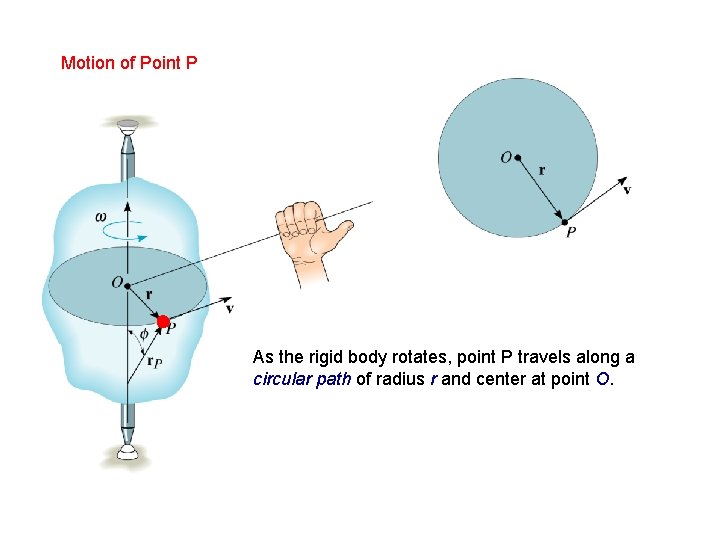
Motion of Point P As the rigid body rotates, point P travels along a circular path of radius r and center at point O.

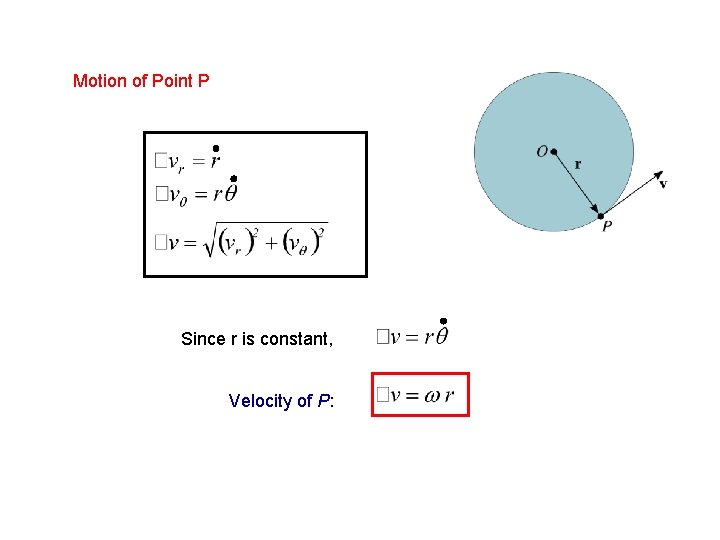
Motion of Point P Since r is constant, Velocity of P:

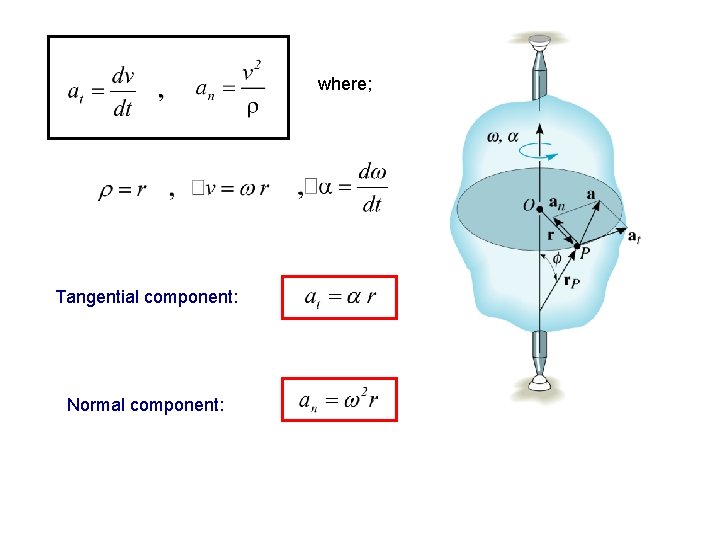
where; Tangential component: Normal component:

If the geometry of the problem is difficult to visualize, the following vector equation should be used: all the vectors should be expressed in terms of its i, j, k,

Example 1 A cord is wrapped around a wheel which is initially at rest. If a force is applied to the cord and gives it an acceleration a = (4 t), determine: a) the angular velocity of the wheel b) the angular position of line OP in radians

[solution] Tangential component: (a. P)t = a r , since the cord is wrapped around the wheel and moves tangent to it. ( +) Integrating, with initial condition that w = 0 at t = 0, ( +)

Integrating, with initial condition that q = 0 at t = 0, ( +) * we cannot use the equation of constant angular acceleration since a is a function of time

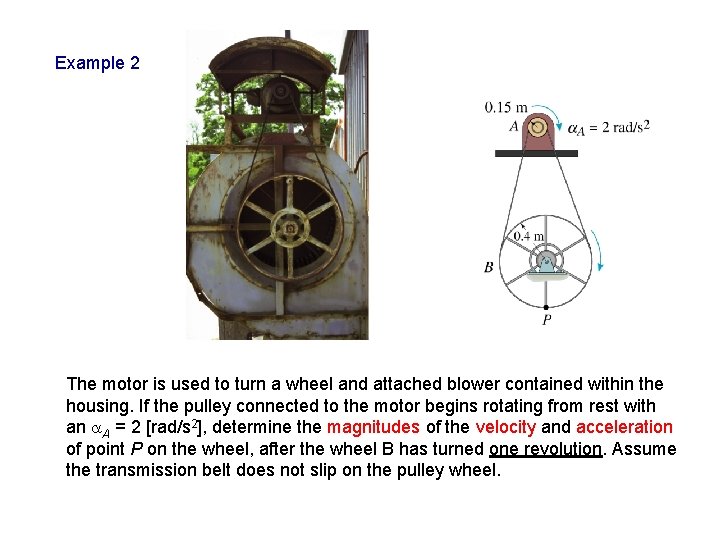
Example 2 The motor is used to turn a wheel and attached blower contained within the housing. If the pulley connected to the motor begins rotating from rest with an a. A = 2 [rad/s 2], determine the magnitudes of the velocity and acceleration of point P on the wheel, after the wheel B has turned one revolution. Assume the transmission belt does not slip on the pulley wheel.

[solution] Convert revolutions → radians; Since the belt does not slip, an equivalent length of belt s must be unraveled from both the pulley and wheel at all times. Thus, Since a. A is constant (always 2 rad/s 2),

The belt has the same speed and tangential component of acceleration as it passes over the pulley and wheel. Thus,

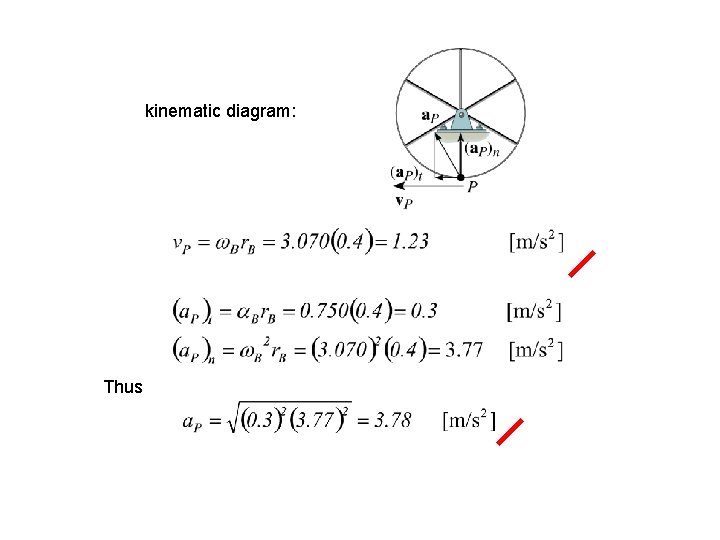
kinematic diagram: Thus

General Plane Motion When a body undergoes general plane motion, it simultaneously translates and rotates. -Absolute Motion Analysis -Relative-Motion Analysis -Instantaneous Center of Zero Velocity -Relative Motion using Rotating Axis

Absolute Motion Analysis If the motion of a point on a body or the angular motion of a line is known, then it may be possible to relate this motion to that of another point or line using an absolute motion analysis. Establish linear position coordinates s / angular position coordinate q are these position coordinates are related using the geometry of the body Time derivatives – get v, a, w, a

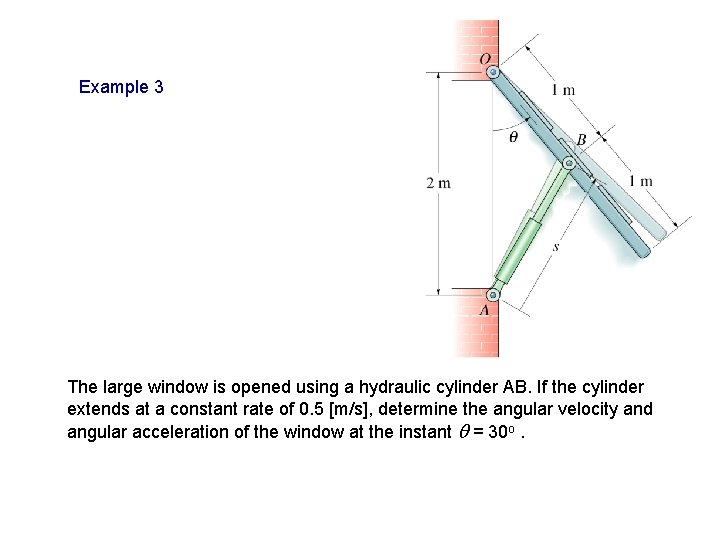
Example 3 The large window is opened using a hydraulic cylinder AB. If the cylinder extends at a constant rate of 0. 5 [m/s], determine the angular velocity and angular acceleration of the window at the instant q = 30 o.

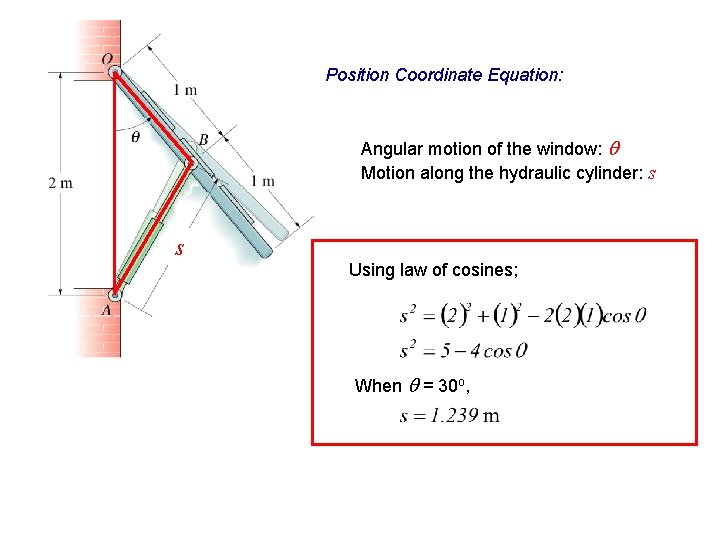
Position Coordinate Equation: Angular motion of the window: q Motion along the hydraulic cylinder: s s Using law of cosines; When q = 30 o,

Time Derivatives: Taking time derivatives of since vs = 0. 5 [m/s], then at q = 30 o,

Taking time derivatives of Since as = dv/dt = 0, then Angular deceleration