Groupes ponctuels point groups Rvision Les axes de

Groupes ponctuels (point groups) Révision : • Les axes de rotation, plans de réflexion, centres d’inversion, rotations impropres et l’identité sont des éléments décrivant des opérations de symétrie particulières • La symétrie de chaque molécule peut être décrite par l’ensemble des opérations de symétrie possibles • les opérations de symétrie peuvent être combinées d’après certaines règles

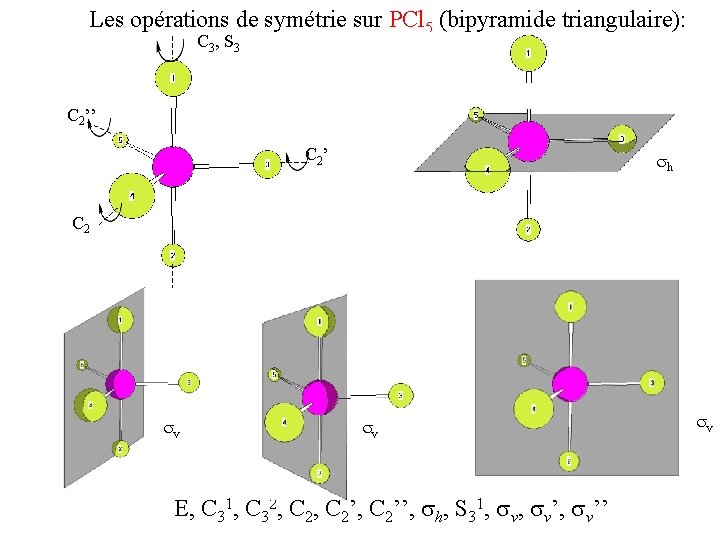
Les opérations de symétrie sur PCl 5 (bipyramide triangulaire): C 3 , S 3 C 2’’ C 2 ’ h C 2 v v E, C 31, C 32, C 2’, C 2’’, h, S 31, v’, v’’ v

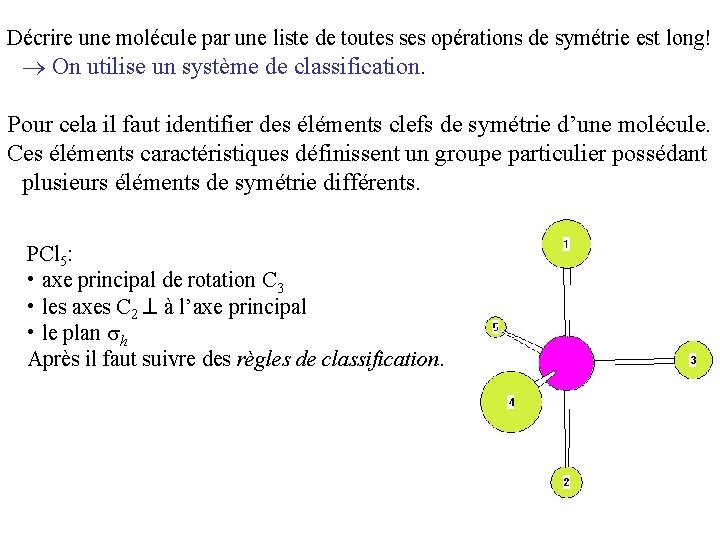
Décrire une molécule par une liste de toutes ses opérations de symétrie est long! On utilise un système de classification. Pour cela il faut identifier des éléments clefs de symétrie d’une molécule. Ces éléments caractéristiques définissent un groupe particulier possédant plusieurs éléments de symétrie différents. PCl 5: • axe principal de rotation C 3 • les axes C 2 à l’axe principal • le plan h Après il faut suivre des règles de classification.

Chaque classification est abrégé par un symbole (symbole de Schönflies). Celui-ci représente une collection d’opérations de symétrie. Il représente un groupe ponctuel (“point group”). Groupe – un groupe d’opérations de symétrie, le terme “groupe” peut être défini mathématiquement Ponctuel – les éléments de symétrie associés aux opérations de symétrie passent par le même point de l’espace. Ce point ne change pas par les opérations de symétrie. (ex. : PCl 5 ce point est situé sur l’atome P). Attention: ce point ne doit pas être nécessairement sur un atome C 6 H 6.

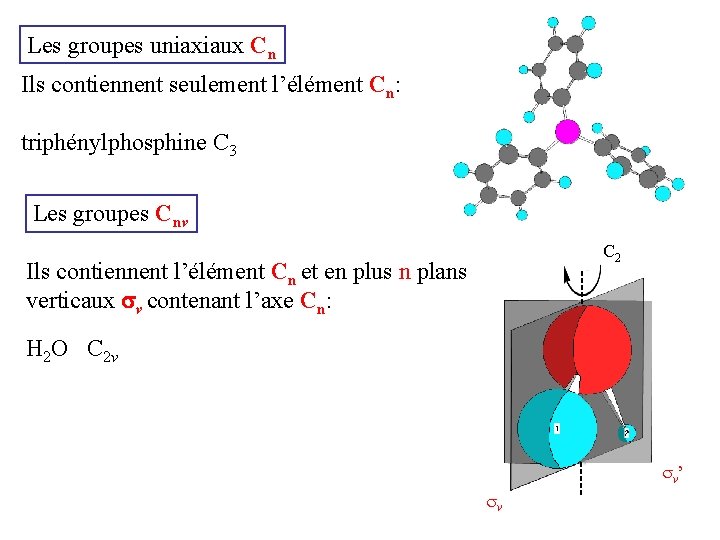
Les groupes uniaxiaux Cn Ils contiennent seulement l’élément Cn: triphénylphosphine C 3 Les groupes Cnv C 2 Ils contiennent l’élément Cn et en plus n plans verticaux sv contenant l’axe Cn: H 2 O C 2 v v’ v

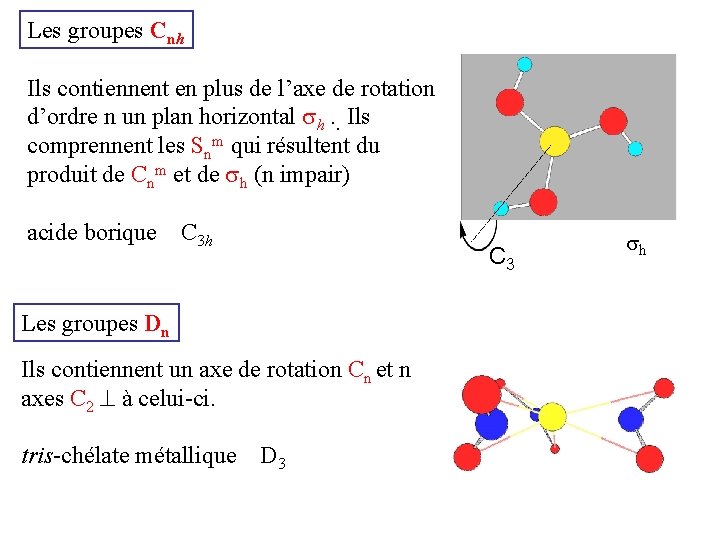
Les groupes Cnh Ils contiennent en plus de l’axe de rotation d’ordre n un plan horizontal h. . Ils comprennent les Snm qui résultent du produit de Cnm et de h (n impair) acide borique C 3 h C 3 Les groupes Dn Ils contiennent un axe de rotation Cn et n axes C 2 à celui-ci. tris-chélate métallique D 3 h

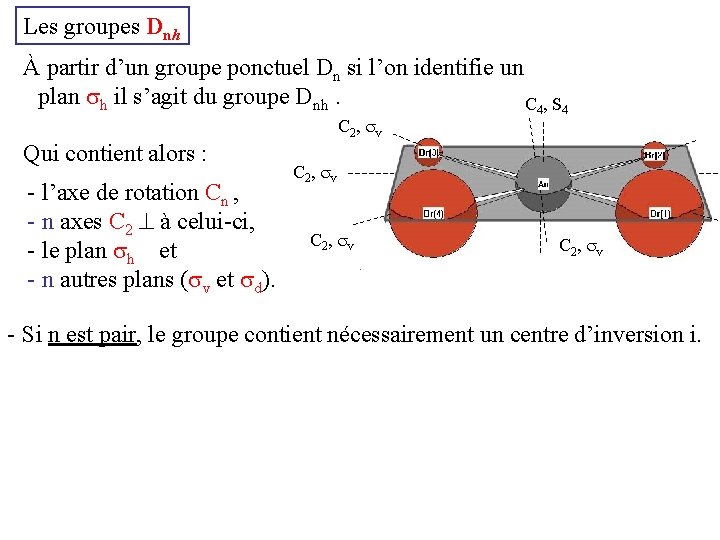
Les groupes Dnh À partir d’un groupe ponctuel Dn si l’on identifie un plan h il s’agit du groupe Dnh. C 4 , S 4 C 2 , v Qui contient alors : - l’axe de rotation Cn , - n axes C 2 à celui-ci, - le plan h et - n autres plans ( v et d). C 2 , v - Si n est pair, le groupe contient nécessairement un centre d’inversion i.

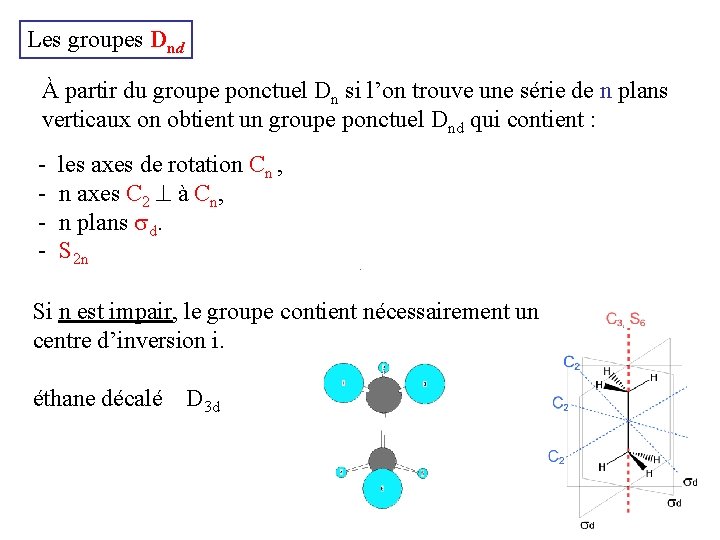
Les groupes Dnd À partir du groupe ponctuel Dn si l’on trouve une série de n plans verticaux on obtient un groupe ponctuel Dnd qui contient : - les axes de rotation Cn , n axes C 2 à Cn, n plans d. S 2 n Si n est impair, le groupe contient nécessairement un centre d’inversion i. éthane décalé D 3 d

Les groupes Sn Ils contiennent seulement l’élément Sn! On peut montrer que pour n impair (n=3, 5, . . ), l’ensemble des opérations autour de cet axe impropre est le même que celui qui forme le group Cnh, donc on parle seulement des groupes Cnh si n est impair pour C 3 h: C 3, C 32, E, h, S 35 pour S 3: S 3, S 32 C 32, S 33 h, S 34 C 3 , S 35, S 36 E Maintenant si n est pair: S 2: S 4: S 2 i groupe Ci S 4 , S 42 C 2 , S 43 , S 44 E les 4 éléments (en gras) forment un groupe. Ce groupe contient toujours un axe Cn/2 colinéaire à Sn.

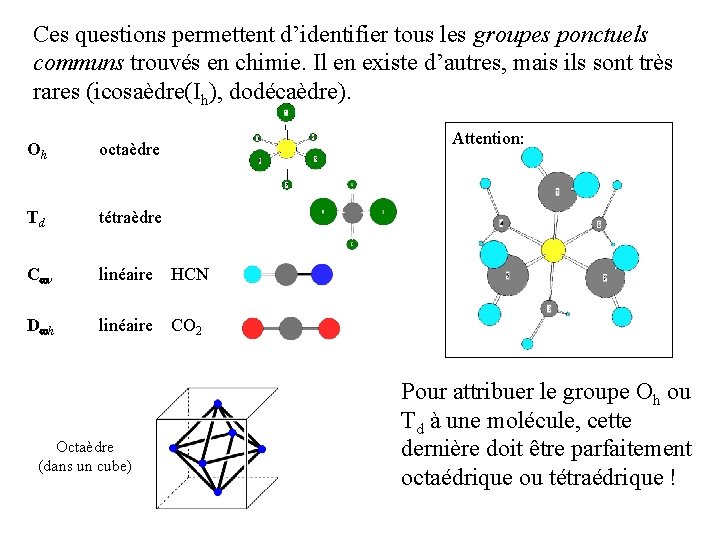
Ces questions permettent d’identifier tous les groupes ponctuels communs trouvés en chimie. Il en existe d’autres, mais ils sont très rares (icosaèdre(Ih), dodécaèdre). Attention: Oh octaèdre Td tétraèdre C v linéaire HCN D h linéaire CO 2 Octaèdre (dans un cube) Pour attribuer le groupe Oh ou Td à une molécule, cette dernière doit être parfaitement octaédrique ou tétraédrique !

Groupes spéciaux (de très haute symétrie) tétraèdre: contient 3 axes S 4, 4 axes C 3 et 6 plans de symétrie d. A ces éléments correspondent 24 opérations de symétrie: S 4, S 42 C 2, S 43 et S 44 E 3 3 = 9 C 3, C 32 et C 33 E 4 2 = 8 d. 6 1 = 6 E = 1 Total = 24 Il n’y a pas de centre d’inversion. exemples: Si. F 4, Cl. O 4 -, Ni(CO)4 Td Oh octaèdre: L’octaèdre et le cube possèdent les mêmes éléments de symétrie. 3 axes C 4 (également S 4), quatre axes C 3 (également S 6), 6 axes C 2’, 3 plans h, 6 plans d. 48 opérations de symétrie exemples: Al. F 6, SF 6, [Fe(CN)6]3 -

Oh 48 opérations de symétrie: C 4, C 42 C 2, C 43 et C 44 E C 3, C 32 et C 33 E C 2’, C 3’ 2 h d. S 4, (S 42 C 2), S 43 et (S 44 E) S 6, S 63 i, S 65 E Total 3 3=9 3 2=8 6 3 2=6 4 2 +1 = 9 1 24

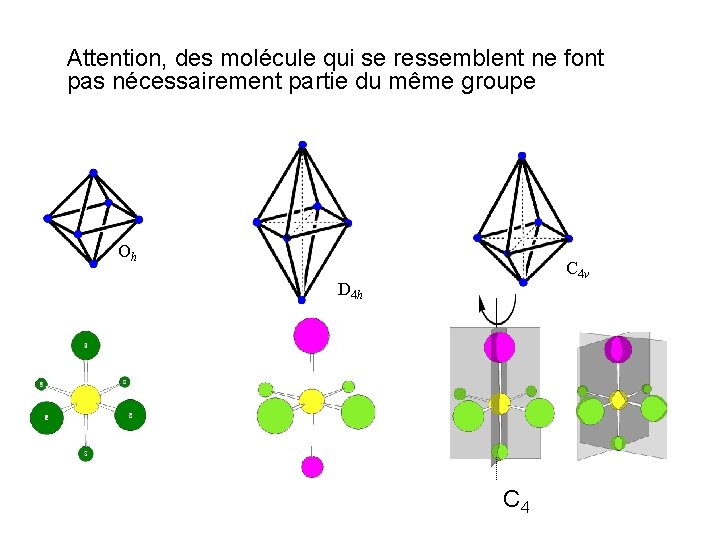
Attention, des molécule qui se ressemblent ne font pas nécessairement partie du même groupe Oh C 4 v D 4 h C 4

Classification: répondre à quelquestions 1. Est-ce que la molécule fait partie des groupes suivants ? octaèdre Oh tétraèdre Td linéaire sans centre d’inversion i C v linéaire avec centre d’inversion i D h NON continuer avec question 2 2. Est-ce que la molécule possède un axe de rotation d’ordre 2 ? OUI continuer avec question 3 La molécule ne possède aucun autre élément d symétrie NON La molécule possède un plan de réflexion La molécule possède un centre d’inversion Ci 3. Est-ce que la molécule possède plus qu’un axe de rotation ? OUI continuer avec question 4 NON La molécule ne possède aucun autre élément de symétrie Cn OUI (n = ordre de l’axe principal, e. g. C 3) Cnh. La molécule possède n plans de réflexion v Cnv. (n = ordre de l’axe principal, e. g. C 3 v) 4. ok et fin La molécule possède un plan de symétrie h (n = ordre de l’axe principal, e. g. C 3 h) La molécule possède un axe S 2 n coaxial avec l’axe principal La molécule possède le groupe ponctuel suivant: Elle ne possède pas d’autre élément de symétrie (n = ordre de l’axe principal, e. g. D 3). Elle possède n plans de réflexion d bissecteur de l’axe C 2 Dnd (n = ordre de l’axe principal, e. g. D 3 d). Elle possède aussi un plan h (n = ordre de l’axe principal, e. g. D 3 h). Classificati on Dnh S 2 n Dn C 1 Cs = C 1 h

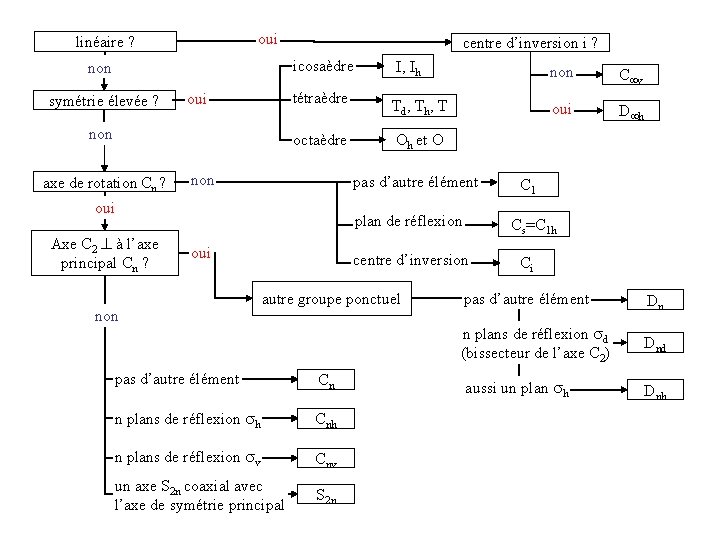
oui linéaire ? non symétrie élevée ? oui non axe de rotation Cn ? centre d’inversion i ? icosaèdre I, Ih non C v tétraèdre Td, Th, T oui D h octaèdre Oh et O non pas d’autre élément oui Axe C 2 à l’axe principal Cn ? plan de réflexion oui non Cs=C 1 h centre d’inversion autre groupe ponctuel pas d’autre élément Cn n plans de réflexion h Cnh n plans de réflexion v Cnv un axe S 2 n coaxial avec l’axe de symétrie principal S 2 n C 1 Ci pas d’autre élément Dn n plans de réflexion d (bissecteur de l’axe C 2) Dnd aussi un plan h Dnh

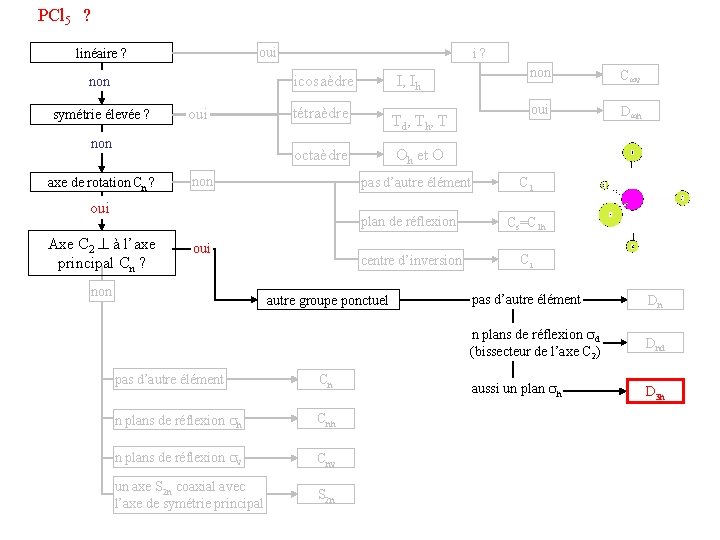
PCl 5 ? oui linéaire ? non symétrie élevée ? oui non axe de rotation Cn ? icosaèdre I, Ih tétraèdre Td, Th, T octaèdre Oh et O non pas d’autre élément oui Axe C 2 à l’axe principal Cn ? oui non Cn n plans de réflexion h Cnh n plans de réflexion v Cnv un axe S 2 n coaxial avec l’axe de symétrie principal S 2 n C v oui D h C 1 plan de réflexion Cs=C 1 h centre d’inversion Ci autre groupe ponctuel pas d’autre élément non pas d’autre élément Dn n plans de réflexion d (bissecteur de l’axe C 2) Dnd aussi un plan h D 3 h

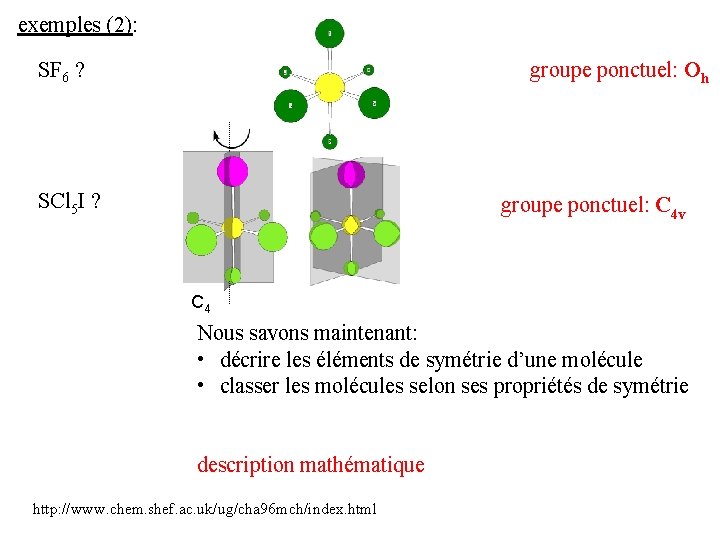
exemples (2): SF 6 ? groupe ponctuel: Oh SCl 5 I ? groupe ponctuel: C 4 v C 4 Nous savons maintenant: • décrire les éléments de symétrie d’une molécule • classer les molécules selon ses propriétés de symétrie description mathématique http: //www. chem. shef. ac. uk/ug/cha 96 mch/index. html

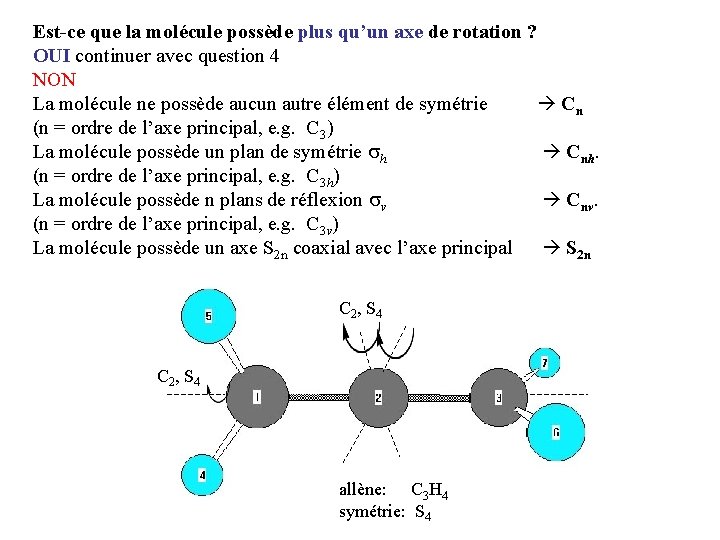
Est-ce que la molécule possède plus qu’un axe de rotation ? OUI continuer avec question 4 NON La molécule ne possède aucun autre élément de symétrie Cn (n = ordre de l’axe principal, e. g. C 3) La molécule possède un plan de symétrie h Cnh. (n = ordre de l’axe principal, e. g. C 3 h) La molécule possède n plans de réflexion v Cnv. (n = ordre de l’axe principal, e. g. C 3 v) La molécule possède un axe S 2 n coaxial avec l’axe principal S 2 n C 2 , S 4 allène: C 3 H 4 symétrie: S 4

Théorie de groupe Définition mathématique d’un groupe Règles pour éléments formant un groupe: 1. La combinaison de deux éléments d’un groupe doit être un élément du groupe 2. Un élément du groupe doit laisser la molécule inchangée : (identité) E 3. La combinaison des éléments d’un groupe doit être associative A(B C) = (A B) C 4. Chaque élément doit posséder un élément inverse (qui est aussi élément du groupe). A A-1 = A-1 A = E Les opérations de symétrie d’une molécule suivent les règles d’un groupe mathématique. Les groupes formés d’opérations de symétrie sont appelés groupes de symétrie ou groupes ponctuels (maintiennent la molécule fixe à un point de l’espace). (Il existe d’autres groupes d’opérations de symétrie, comme en cristallographie, il y a la translation, les groupes spatiaux). La mathématique des groupes permet de simplifier les équations pour calculer les énergies d’une molécule : application en mécanique quantique, en spectroscopie, thermodynamique…

Les groupes ponctuels de symétrie peuvent se partager en deux catégories : Si la multiplication est commutative: AB = BA groupe abélien Si la multiplication n’est pas commutative: AB BA groupe non-abélien exemple: opérations de symétrie E, C 2 , v’ Est-ce que ces opérations forment un groupe ? table de multiplication: E C 2 v v’ E E C 2 v v’ C 2 E v’ v v’ E C 2 v’ v C 2 E

E C 2 v v’ E E C 2 v v’ C 2 E v’ v v’ E C 2 v’ v C 2 E table de multiplication: - Les 16 produits possibles sont tous des éléments du groupe. - La combinaison des éléments est associative (à vérifier) - Dans le cas présent : chaque élément est son propre inverse ces 4 éléments forment le groupe C 2 v C 2 v = v C 2 , v’ v = v v’, etc…. C 2 v est un groupe abélien

Exemple : groupe C 3 v (NH 3) Les opérations de symétrie de ce groupe sont: E, C 31 , C 32 , sv’, sv’’ ne pas oublier que C 31 * v’ = v’’ tableau de multiplication : E C 32 v v’’ E E C 32 v v’’ C 3 C 32 E v’’ v v’ C 32 E C 3 v’’ v v’ v’’ E C 32 v’ v’’ v C 32 E C 3 v’’ v v’ C 32 E groupe non-abélien C 3 v Compliqué!

Pour résoudre plus facilement la question de la multiplication des colonnes, une méthode plus rapide est possible. Il s’agit de trouver une solution non triviale aux opérations de symétrie de ce groupe en remplaçant chaque opération par un 1 ou un -1, la solution devant respecter les autres opérations de symétrie. Pour le groupe C 2 v les opérations de symétrie sont : E, C 2 , v’ On dit que E = 1, C 2 = 1 , v = -1, v’ = -1 Cette solution n’est valide que si toute les multiplications d’opérations restent valides. Les résultats doivent être les mêmes : v * v’ = C 2 E * C 2 = C 2 v * C 2 = v’ -1 *-1 = 1 1 *-1 =-1 . . . Les résultats sont les mêmes donc la solution est valide

Exemple : Groupe C 2 v: Les réponses suivantes (et non triviales) sont possibles: E=1 E=1 v = 1 v = -1 C 2 = -1 v’ = 1 v’ = -1 v’ = 1 La table de multiplication de C 2 v est : E C 2 v v’ E E C 2 v v’ C 2 E v’ v v’ E C 2 v’ v C 2 E Il est possible de représenter les opérations de symétrie par des opérations mathématiques: «rotation de 180°» = «multiplier par 1» ou «multiplier par -1» selon la représentation considérée. 1 -1 1 -1 -1 -1 1 C 2 v E C 2 v v’ G 1 1 1 G 2 1 1 -1 -1 G 3 1 -1 G 4 1 -1 -1 1

Représentations Considérons: opérations de symétrie: tourner à droite tourner à gauche faire demi-tour rester immobile Ces quatre opérations forment un groupe D G R E dans un repère bidimensionnel (2 D): x D y y’=-x x’=y Les coordonnées cartésiennes peuvent être utilisées comme base mathématique de la représentation.

x R y y’’=-y x’’=-x La même chose pour les opérations G et E Chaque opérateur peut être ensuite converti en matrice : Comment faire la transformation Avec la notation matricielle : ?

Représentation matricielle de chacune des opérations de symétrie : Ces matrices constituent un groupe! L’élément inverse est l’élément qui permet de faire un retour en arrière sur une opération, c’est-à-dire que l’on retourne à la case de départ. Pour ce groupe l’élément inverse de G est D:

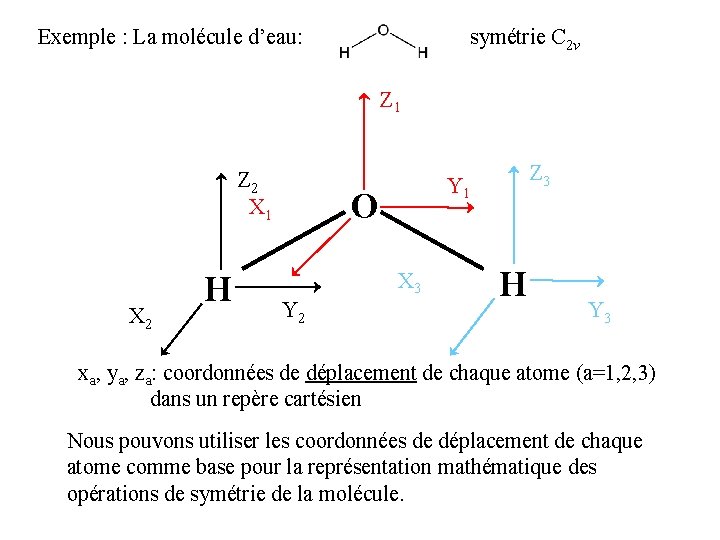
Exemple : La molécule d’eau: symétrie C 2 v Z 1 Z 2 X 1 X 2 H O X 3 Y 2 Z 3 Y 1 H Y 3 xa, ya, za: coordonnées de déplacement de chaque atome (a=1, 2, 3) dans un repère cartésien Nous pouvons utiliser les coordonnées de déplacement de chaque atome comme base pour la représentation mathématique des opérations de symétrie de la molécule.

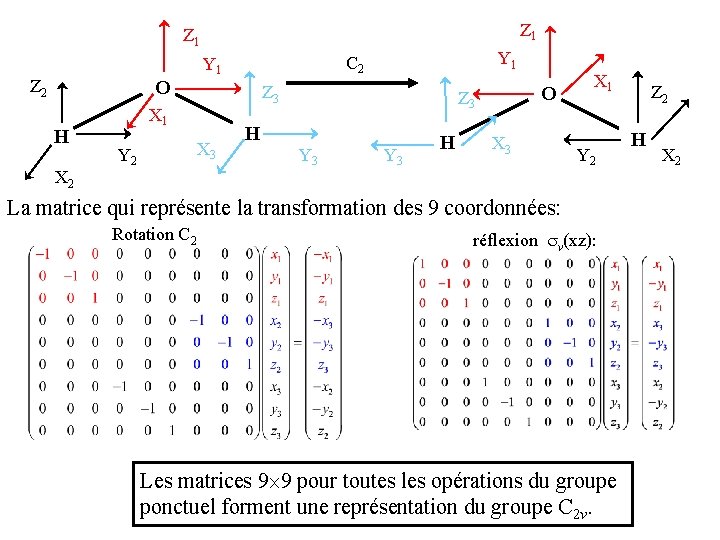
Z 1 Z 2 O H X 2 Z 3 X 1 X 3 Y 2 Y 1 C 2 Y 1 O Z 3 H Y 3 H X 3 X 1 Y 2 La matrice qui représente la transformation des 9 coordonnées: Rotation C 2 réflexion v(xz): Les matrices 9 9 pour toutes les opérations du groupe ponctuel forment une représentation du groupe C 2 v. Z 2 H X 2

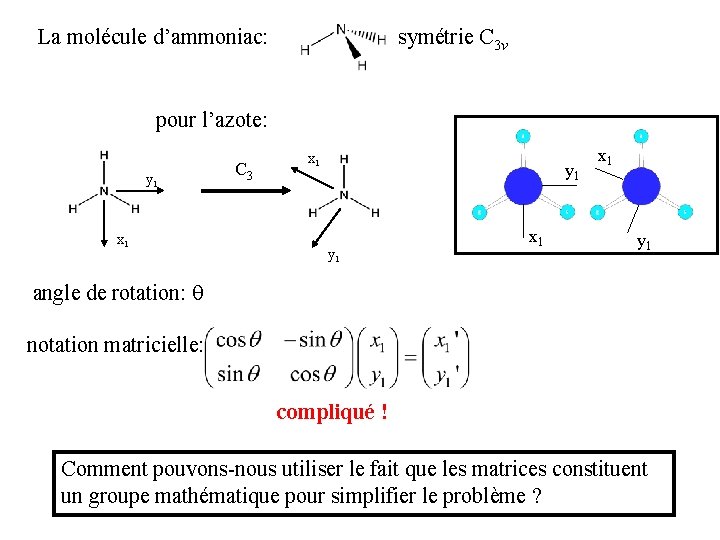
La molécule d’ammoniac: symétrie C 3 v pour l’azote: y 1 x 1 C 3 x 1 y 1 angle de rotation: q notation matricielle: compliqué ! Comment pouvons-nous utiliser le fait que les matrices constituent un groupe mathématique pour simplifier le problème ?

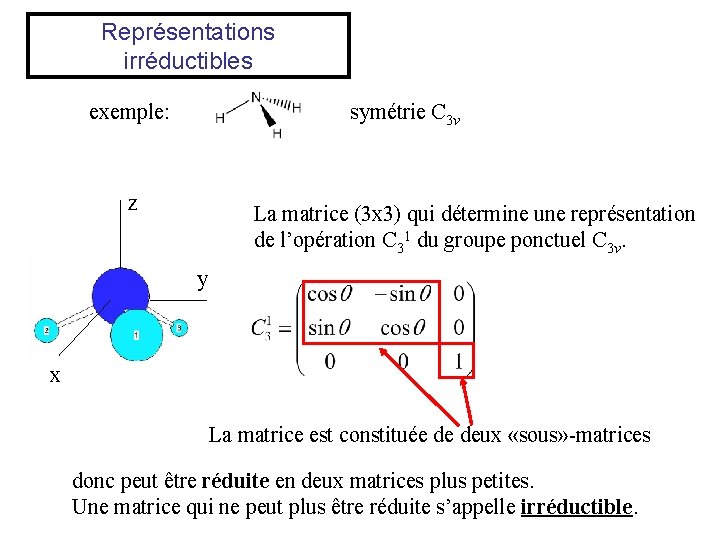
Représentations irréductibles exemple: symétrie C 3 v z La matrice (3 x 3) qui détermine une représentation de l’opération C 31 du groupe ponctuel C 3 v. y x La matrice est constituée de deux «sous» -matrices donc peut être réduite en deux matrices plus petites. Une matrice qui ne peut plus être réduite s’appelle irréductible.

Conséquence pour la théorie des groupes appliquée à la chimie: Certaines représentations de dimension supérieure à un peuvent être réduites en des représentations de plus petites dimensions. Une représentation matricielle qui peut être réduite est appelée représentation réductible. Une représentation qui ne peut pas être réduite en des représentations de plus petite dimension est appelée représentation irréductible. Nous pouvons trouver n’importe quelle représentation matricielle des opérations de symétrie d’une molécule et cette représentation pourra toujours s’exprimer en termes de représentation irréductible du groupe ponctuel de la molécule. La bonne nouvelle: Toutes les représentations irréductibles ont été déterminées pour chacun des groupes ponctuels utilisés en chimie!

Caractères Un problème: Comment manipuler des matrices volumineuses ? (H 2 O: 3 x 3, C 6 H 6 !!!) Une matrice 4 x 4 quelconque: la trace de cette matrice est a+f+k+p

En théorie des groupes appliquée à la chimie, cette trace de la représentation matricielle est caractéristique de son comportement en tant que représentation d’une opération de symétrie. Les représentations matricielles ne voient pas la valeur de leur trace changer sous l’effet de toutes les transformations mathématiques mises en jeu. Parce que la trace est caractéristique de la matrice on l’appelle caractère de la matrice. Cette propriété simplifie beaucoup l’utilisation des matrices en théorie des groupes appliquée à la chimie. Il faut simplement connaître la valeur des traces des représentations matricielles irréductibles (et il n’est pas nécessaire d’écrire les matrices dans leur intégralité).

Le cœur de la théorie des groupes Qu’avons-nous appris des mathématiques: 1. Nous pouvons représenter mathématiquement une molécule (généralement à l’aide des coordonnées de ses atomes). Cette description mathématique de la molécule forme une base pour les opérations de symétrie. 2. A l’aide de cette base nous pouvons créer des représentations mathématiques des opérations de symétrie à l’aide de règles simples. 3. Les représentations mathématiques sont soit réductibles, soit irréductibles. Toute représentation réductible peut être exprimée comme une combinaison de représentations irréductibles. 4. Les représentations peuvent être exprimées simplement par des nombres appelés caractères. 5. Les représentations irréductibles de tous les groupes ponctuels courants ont été déterminées. Ces représentations sont regroupées dans des tables de caractères.

Nous avons vu : - Toute molécule peut être classée selon ses opérations de symétrie dans un groupe ponctuel. - Le groupe ponctuel d’une molécule définit l’ensemble des opérations de symétrie de la molécule. - Certaines opérations de symétrie se comportent de manière semblable et peuvent être regroupées en classes d’équivalence.

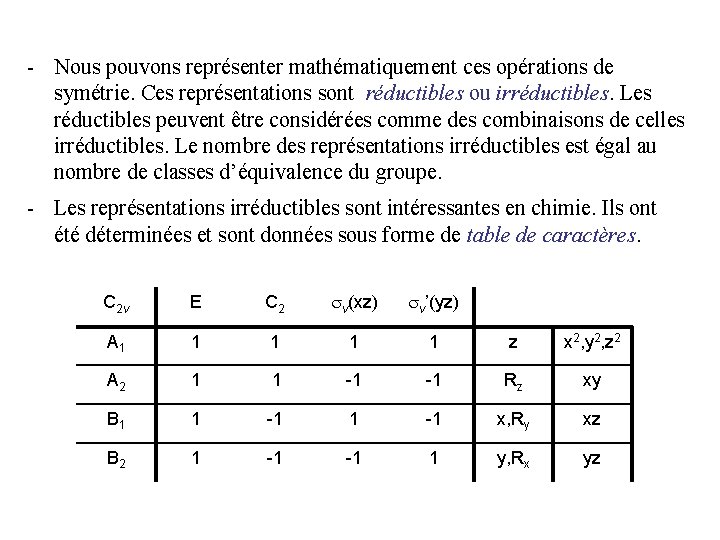
- Nous pouvons représenter mathématiquement ces opérations de symétrie. Ces représentations sont réductibles ou irréductibles. Les réductibles peuvent être considérées comme des combinaisons de celles irréductibles. Le nombre des représentations irréductibles est égal au nombre de classes d’équivalence du groupe. - Les représentations irréductibles sont intéressantes en chimie. Ils ont été déterminées et sont données sous forme de table de caractères. C 2 v E C 2 v(xz) v’(yz) A 1 1 1 z x 2, y 2, z 2 A 2 1 1 -1 -1 Rz xy B 1 1 -1 x, Ry xz B 2 1 -1 -1 1 y, Rx yz

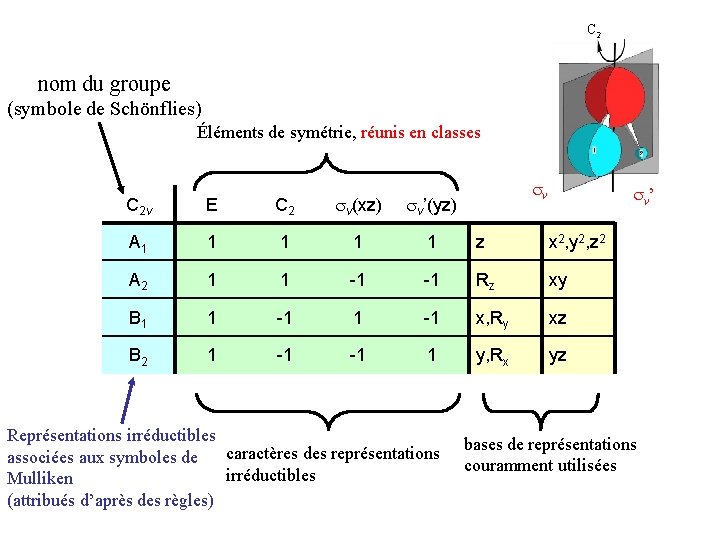
C 2 nom du groupe (symbole de Schönflies) Éléments de symétrie, réunis en classes v v’ C 2 v E C 2 v(xz) v’(yz) A 1 1 1 z x 2, y 2, z 2 A 2 1 1 -1 -1 Rz xy B 1 1 -1 x, Ry xz B 2 1 -1 -1 1 y, Rx yz Représentations irréductibles caractères des représentations associées aux symboles de irréductibles Mulliken (attribués d’après des règles) bases de représentations couramment utilisées

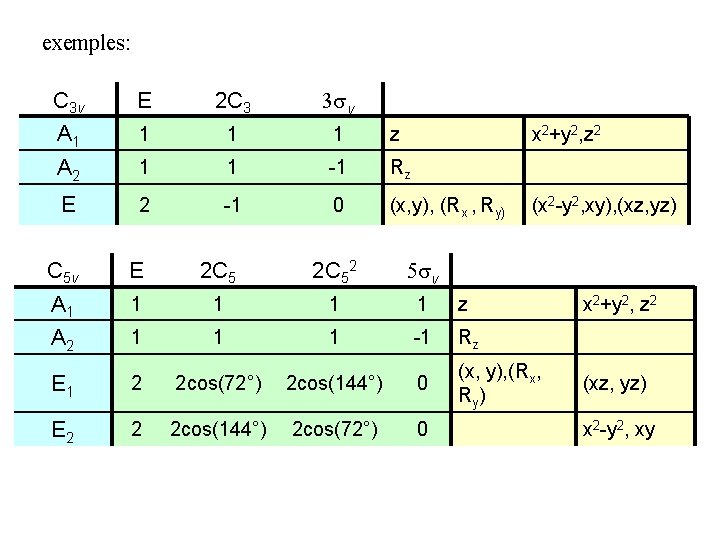
exemples: C 3 v E 2 C 3 3 v A 1 1 z A 2 1 1 -1 Rz E 2 -1 0 (x, y), (Rx , Ry) x 2+y 2, z 2 (x 2 -y 2, xy), (xz, yz) C 5 v E 2 C 52 5 v A 1 1 1 z A 2 1 1 1 -1 Rz E 1 2 2 cos(72°) 2 cos(144°) 0 (x, y), (Rx, Ry ) E 2 2 2 cos(144°) 2 cos(72°) 0 x 2+y 2, z 2 (xz, yz) x 2 -y 2, xy

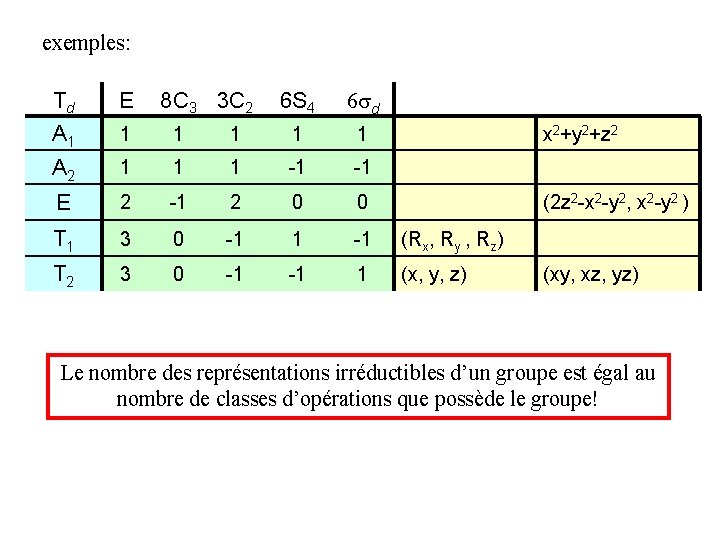
exemples: 6 S 4 6 d 1 1 1 -1 -1 2 0 0 T 1 3 0 -1 1 -1 (Rx, Ry , Rz) T 2 3 0 -1 -1 1 (x, y, z) Td E 8 C 3 3 C 2 A 1 1 1 A 2 1 E x 2+y 2+z 2 (2 z 2 -x 2 -y 2, x 2 -y 2 ) (xy, xz, yz) Le nombre des représentations irréductibles d’un groupe est égal au nombre de classes d’opérations que possède le groupe!

Les classes On peut décrire la symétrie d’une molécule grâce à un ensemble d’éléments de symétrie qui peuvent être effectuées sur la molécule donc un ensemble d’opérations de symétrie. Ces opérations de symétrie peuvent être utilisées pour définir la symétrie de la molécule. Les opérations de symétrie qui peuvent être appliquées sur la molécule PH 3 (ou NH 3) sont: E, C 31, C 32, v’ et v’’. Certaines de ces opérations de symétrie sont semblables: C 31 et C 32. sv, sv’ et sv’’. E (seul) Classes d’équivalence: La molécule PH 3 possède les classes d’équivalence E, 2 C 3, 3 v. Les chiffres 2, 3 indiquent le nombre d’opérations de symétrie dans une classe d’équivalence: 2 C 3 contient C 31 et C 32.

Comment assigner les opérations de symétrie aux classes ? 1. L’identité E est toujours une classe en soi 2. L’inversion i est toujours une classe en soi 3. La rotation autour de Cnk et son inverse (Cn-k = Cnn-k) sont dans la même classe si : - n plans v ou d existent - n axes C 2 à Cnk existent 4. Règle 3 est aussi valable pour les rotations impropres Sn 5. Dans le groupe Cnv tous les v sont dans la même classe. Dans le groupe Dnh les v et les d sont dans des classes différentes, une réflexion h est toujours une autre classe. 6. Dans le groupe Dnd tous les axes C 2’ ( à l’axe principal) sont dans la même classe. Dans le groupe Dnh les axes C 2’ ( à l’axe principal) ne sont pas tous dans la même classe. 7. Règle 6 est aussi valable pour les axes impropres de rotation.

Plus court: Deux opérations se trouvent dans la même classe si (1) les deux sont du même genre (rotation, réflexion) (2) dans le groupe existe une autre opération qui inter-change les deux opérations dans C 6 : les rotations sont toutes dans des classes différentes, dans C 6 v : la réflexion dans un plan vertical inter-change l’effet de rotation de 60° et de 300°, donc C 61 et C 65 sont dans la même classe

Comment réduire une représentation réductible? C 3 v E 2 C 3 3 v A 1 1 z A 2 1 1 -1 Rz E 2 -1 0 (x, y), (Rx , Ry) x 2+y 2, z 2 (x 2 y 2, xy), (xz, yz) ci(R): le caractère de la représentation irréductible d’indice i pour un élément de symétrie c (R): le caractère de la représentation réductible pour un élément de symétrie h: l’ordre du groupe (le nombre d’opérations de symétrie qu’il contient) n. R: l’ordre de la classe de symétrie considérée ai: le nombre de fois que la représentation irréductible d’indice i apparaît dans la représentation réductible la formule de réduction

exemple: représentation réductible du groupe C 3 v: table de caractère du groupe C 3 v: C 3 v E 2 C 3 3 v A 1 1 z A 2 1 1 -1 Rz 0 (x, y), (Rx , Ry) E h=6: 2 -1 C 3 v E 2 C 3 3 v RR 4 1 0 1(de E) + 2(de C 3) + 3(de v) = 6 C 3 v E 2 C 3 3 v RR 4 1 0 x 2+y 2, z 2 (x 2 y 2, xy), (xz, yz) Le nombre de fois que A 1 apparaît dans la représentation réductible RR

exercice: Combien de fois peut-on trouver les représentations A 2 et E dans la représentation réductible (RR) du groupe C 3 v ? C 3 v E 2 C 3 3 v RR 4 1 0 C 3 v E 2 C 3 3 v A 1 1 A 2 1 1 -1 E 2 -1 0 RR = A 1+A 2+E

exercice: représentation réductible (RR) du groupe tétraèdre Td Td E 8 C 3 3 C 2 6 S 4 6 v RR 7 1 -1 -1 -1 A 1 1 1 A 2 1 1 1 -1 -1 E 2 -1 2 0 0 T 1 3 0 -1 1 -1 T 2 3 0 -1 -1 1 RR = A 2+T 1+ T 2