Cristallographie Gomtrique D ZAKARIA PLAN DU COURS I

Cristallographie Géométrique( D. ZAKARIA) PLAN DU COURS I – INTRODUCTION II – CRISTALLOGRAPHIE GEOMETRIQUE 1 – RESEAU DIRECT OU REEL (R. D. ) 2 – RESEAU RECIPROQUE (R. R. ) 3 – SYMETRIE DU RESEAU CRISTALLIN a – Symétries d’orientation (symétries ponctuelles) b – Symétries de position (symétrie de recouvrement) III – RAYONS X ET PHENOMENE DE DIFFRACTION

Cristallographie Géométrique( D. ZAKARIA) 3 – SYMETRIE DU RESEAU CRISTALLIN - Echelle macroscopique D’après la 1ère loi de la cristallographie, les normales des faces ne change pas d’orientation. L’ensemble de ces demi droites présente des éléments de symétrie - Echelle microscopique Le réseau cristallin est un réseau de motifs (translation), le motif lui-même est symétrique. Donc, la matière cristallisée présente dans sa structure des caractères de symétrie à l’échelle microscopique ou macroscopique. Une opération de symétrie fait passer le cristal d’une position initiale à une position finale indiscernables Deux types de symétrie – Symétries d’orientation (symétries ponctuelles) – Symétries de position (symétries de recouvrement)

Cristallographie Géométrique( D. ZAKARIA) a – Symétries d’orientation (symétries ponctuelles) Sont des symétries qui doivent transformer des demi-droites issues d’un même point et perpendiculaire aux faces du cristal. Il n’en existe que trois types : 1 - Rotation autour d’un axes avec un angle de θ = 2π/n (n ordre de l’axe) 2 - Inversion par rapport à un point (centre de symétrie) 3 - Réflexion par rapport à un plan (miroir) La combinaison de 1 et 2 conduit à un 4ème type : la rotation-inversion (rotation puis inversion % à un centre de symétrie sur l’axe de rotation)

Cristallographie Géométrique( D. ZAKARIA) i – Rotation - Elle s’effectue autour d’un axe (axe de rotation) - L’angle de rotation θ = 2π/n (n doit être entier) - n est l’ordre de la rotation l’axe de rotation est noté An ou n Exemple L’angle de rotation est θ = π = 2π/2 Axe de rotation d’ordre 2 (noté A 2 ou 2) z A 2 Dans un repère orthonormé l’opération A 2 // à l’axe z y est représenté par la matrice M(A 2) tel que : x 2 z x = M(A 2) y z -1 0 0 M(A 2) = 0 -1 0 0 0 1 Les positions et sont dites équivalentes, elles se déduisent l’une de l’autre par une opération de symétrie (A 2) A 2 est représenté par : si A 2 au plan de projection si A 2 // au plan de projection

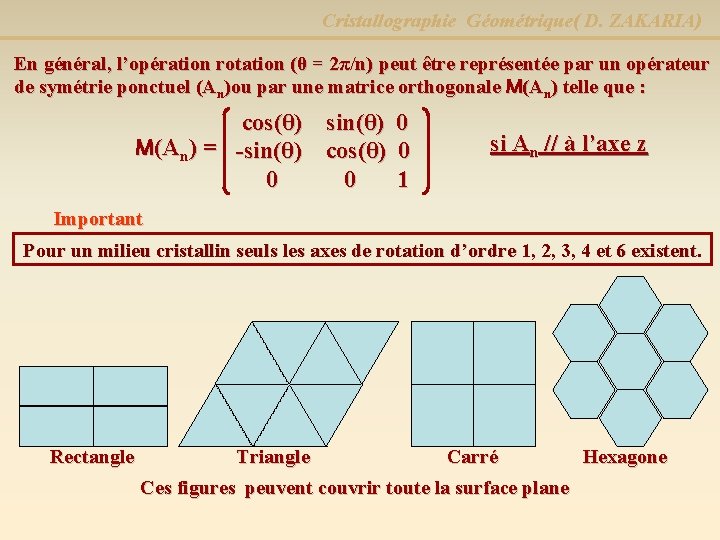
Cristallographie Géométrique( D. ZAKARIA) En général, l’opération rotation (θ = 2π/n) peut être représentée par un opérateur de symétrie ponctuel (An)ou par une matrice orthogonale M(An) telle que : cos(θ) sin(θ) 0 M(An) = -sin(θ) cos(θ) 0 0 0 1 si An // à l’axe z Important Pour un milieu cristallin seuls les axes de rotation d’ordre 1, 2, 3, 4 et 6 existent. Rectangle Triangle Carré Ces figures peuvent couvrir toute la surface plane Hexagone

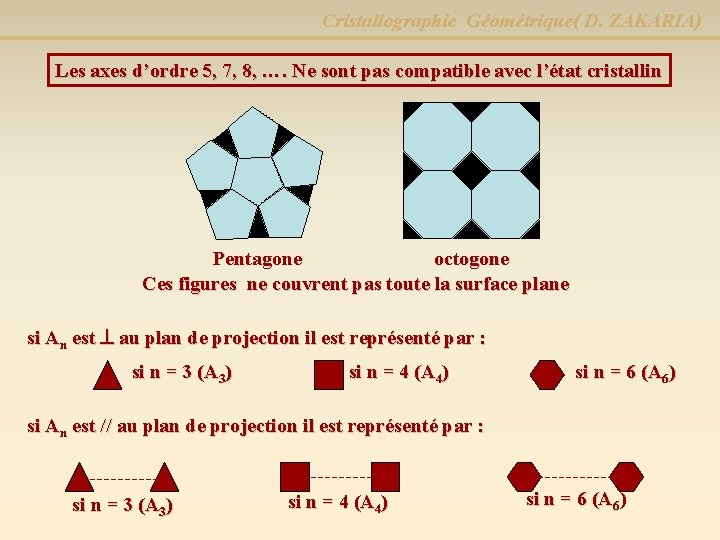
Cristallographie Géométrique( D. ZAKARIA) Les axes d’ordre 5, 7, 8, …. Ne sont pas compatible avec l’état cristallin Pentagone octogone Ces figures ne couvrent pas toute la surface plane si An est au plan de projection il est représenté par : si n = 3 (A 3) si n = 4 (A 4) si n = 6 (A 6) si An est // au plan de projection il est représenté par : si n = 3 (A 3) si n = 4 (A 4) si n = 6 (A 6)

Cristallographie Géométrique( D. ZAKARIA) ii – Inversion Elle s’effectue par rapport à un point (centre d’inversion ou centre de symétrie) noté i z x i i y M(i) = Un centre de symétrie est représenté par : -1 0 0 0 -1 0 0 0 -1

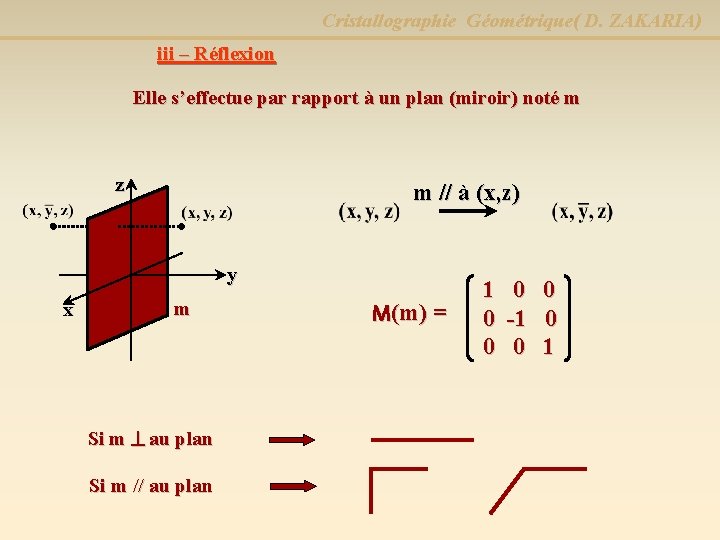
Cristallographie Géométrique( D. ZAKARIA) iii – Réflexion Elle s’effectue par rapport à un plan (miroir) noté m z m // à (x, z) y x m Si m au plan Si m // au plan M(m) = 1 0 0 0 -1 0 0 0 1

Cristallographie Géométrique( D. ZAKARIA) iiii – Rotation-inversion Combinaison de deux opérations de symétrie : - rotation d’un angle θ = 2π/n (n doit être entier) - inversion % à un centre de symétrie sur l’axe de rotation) L’axe de rotation inversion (ou axe inverse) est noté An ou n Exemple L’angle de rotation est θ = π = 2π/2 Axe de rotation d’ordre 2 (noté A 2 ou 2) z A 2 // à z y m x 2 x y z -1 0 0 = 0 -1 0 0 0 -1 M(i) -1 0 0 0 -1 0 0 0 1 M(A 2) 1 0 0 M(A 2) = M(i) x M(A 2) = 0 1 0 = M(m) 0 0 -1 x y z

Cristallographie Géométrique( D. ZAKARIA) 2 m Donc (la réflexion est une opération de symétrie inverse) Pour un axe impropre d’ordre n (An) -cosθ sinθ 0 M(An) = M(i) x M(An) = -sinθ -cosθ 0 0 0 -1 Les axes impropres sont notés par : A 2 (ou 2) A 1 (ou 1) A 3 (ou 3) m (miroir) i (centre d’inversion) 3 + i A 4 (ou 4) A 6 (ou 6) Existence d’un axe 2 3/m (3 m)

Cristallographie Géométrique( D. ZAKARIA) Positions équivalentes (ou points équivalents) Les positions équivalentes sont toutes les positions qui se déduisent les une des autres par l’application des opérations de symétrie d’un élément de symétrie Afin de déterminer l’ensemble de positions équivalents pour un élément ou un ensemble d’élément de symétrie, on utilise une représentation pratique appelée « Projection stéréographique »

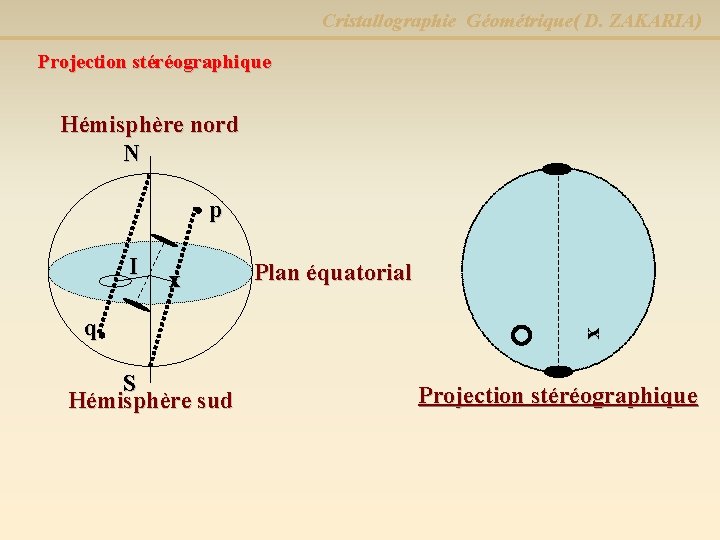
Cristallographie Géométrique( D. ZAKARIA) Projection stéréographique Hémisphère nord N p I x S Hémisphère sud x q Plan équatorial Projection stéréographique

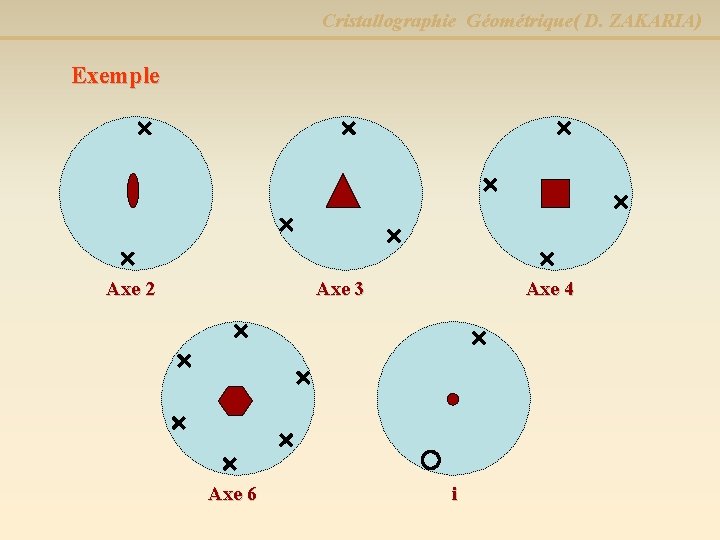
Cristallographie Géométrique( D. ZAKARIA) Exemple Axe 2 Axe 3 Axe 6 Axe 4 i

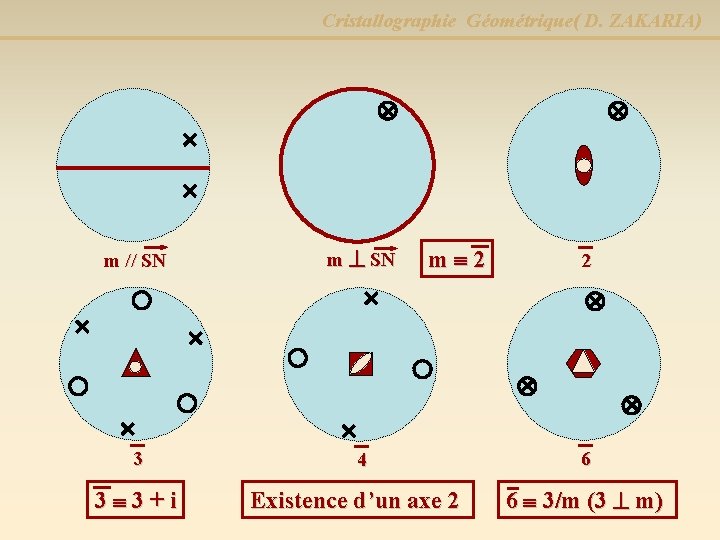
Cristallographie Géométrique( D. ZAKARIA) m // SN m SN 3 4 6 3 3 + i Existence d’un axe 2 6 3/m (3 m) m 2 2

Cristallographie Géométrique( D. ZAKARIA) Combinaisons des symétries ponctuelles cristallines Les combinaisons possibles ne sont pas des combinaisons dues au hasard. Elles obéissent à des règles « THEORIE DES GROUPES » En mathématique, un groupe est un ensemble d’éléments liés entre eux par 4 règles fondamentales Règle I : Le produit de 2 éléments quelconques du groupe ainsi que le carré de chaque élément du groupe doit être un élément du groupe Règle II : Un élément parmi les éléments du groupe doit permuter avec tous les autres et les laisser inchangés : c’est l’élément identité (neutre). Règle III : La multiplication est associative Règle IV : Chaque élément doit avoir un élément réciproque ou inverse qui est aussi un élément du groupe. L’ensemble des opérations de symétrie ponctuelle doit constituer un groupe au sens mathématique du terme.

Cristallographie Géométrique( D. ZAKARIA) Exemples - Règle I - Le produit d’une rotation d’ordre 2 (// oz) par une inversion i ( 1 ) est identique à un miroir m dans le plan xoy 2 x 1 = m - De même : 3 (//oz) x m ( oz) = 6 2 x 2 = 22 = 1 m x m = m 2 = 1 N. B. : axe de rotation d’ordre 1 l’angle de rotation θ = 2π/1

Cristallographie Géométrique( D. ZAKARIA) Exemples - Règle II L’élément identité (neutre) existe : c’est la rotation d’ordre 1. Cet élément est implicitement contenu dans tout axe de rotation 22, 33, 44, 66. - Règle III Les opérations de symétrie sont représentées par des matrices. la multiplication matricielle est associative. - Règle IV Opération de rotation d’ordre n l’angle de rotation θ = 2π/n Opération inverse de rotation d’ordre n l’angle de rotation θ = (2π - 2π/n) (identique à une rotation 2π/n mais dans le sens inverse) 3 x 3 -1 = 1

Cristallographie Géométrique( D. ZAKARIA) Remarques et théorèmes 1 - Tous les éléments de symétrie d'une figure finie se coupent au moins en un point 2 - Si un axe d'ordre pair est perpendiculaire à un miroir, l'intersection est un centre de symétrie 3 - Si une figure n'a qu'un axe de symétrie, tout plan de symétrie doit passer par cet axe ou lui être perpendiculaire 4 - Si un axe d'ordre n est dans un plan de symétrie alors il existe n plans de symétrie formant entre eux des angles de π/n 5 - S'il existe un seul axe d'ordre supérieur à 2, tout axe d'ordre 2 doit lui être perpendiculaire 6 - Si un axe d'ordre 2 est perpendiculaire à un axe d'ordre n, il existe n axes d'ordre 2 qui lui sont perpendiculaires et formant entre eux des angles de π/n 7 - L'existence de plans miroirs horizontaux et verticaux entraîne l'existence d'axes d'ordre 2 à leur intersection

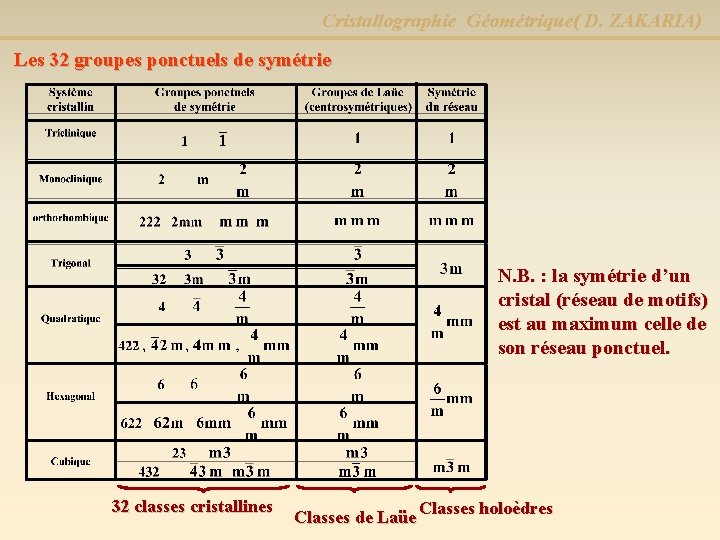
Cristallographie Géométrique( D. ZAKARIA) Lorsqu’une figure possède un ou plusieurs éléments de symétrie, l’ensemble des opérations de symétrie ponctuelle doit constituer un groupe au sens mathématique du terme. Les 32 groupes ponctuels de symétrie (G. P. S. ) (ou bien les 32 classes cristallines) - 5 G. P. S. (classes cristallines) formés par un seul axe n (1, 2, 3, 4 ou 6) - 17 G. P. S. (classes cristallines) obtenus en associant à chacun des dix éléments (n ou n) un ou deux éléments de symétrie binaire 2/m , 4/m , 6/m , 222 , 32 , 422 , 622 , 2 mm , 3 m , 4 mm , 6 mm , 32/m , 42 m , 62 m , mmm , 4/mmm , 6/mmm - 5 G. P. S. (classes cristallines) formés par plusieurs axes de rotation d’ordre n > 2 (système cubique) 233 , 432 , 43 m , m 3 m

Cristallographie Géométrique( D. ZAKARIA) Remarques : * Parmi les 32 groupes ponctuels, - 7 groupes ont la symétrie du réseau ponctuel groupes holoèdres - 25 groupes ont une symétrie < à celle du réseau ponctuel groupes mérièdres - 11 sont centro-symétriques groupes de Laüe * Le degré de symétrie (S) d’un groupe ponctuel ou classe cristalline est égale au nombre de positions obtenues par application de toutes les opérations de symétrie du groupe à un point situé en dehors de tout élément de symétrie S = 1 + n 2 + 2 n 3 + 3 n 4 + 5 n 6 Avec ni = nombre d’axe de rotation d’ordre i Si le groupe possède un centre de symétrie Exemple : Pour le groupe 222 S = 4 (triclinique) 1 ≤ S ≤ 48 (cubique) S’ = 2 S

Cristallographie Géométrique( D. ZAKARIA) Notation du G. P. S. On utilise soit : - La notation descriptive : présentation de tous les éléments de symétrie - La notation d’HERMAN-MAUGIN : se limite aux éléments de symétrie indépendants et générateurs du groupe. Exemples : Le groupe mmm (notation d’HERMAN-MAUGIN) notation descriptive mmm De même : m 3 3 , m 3 m 3 - Si un miroir m contient un axe d’ordre n le groupe est noté nm(exemple : 3 m) n 2 - Si un miroir m est à un axe d’ordre n le groupe est noté (exemple : ) m m

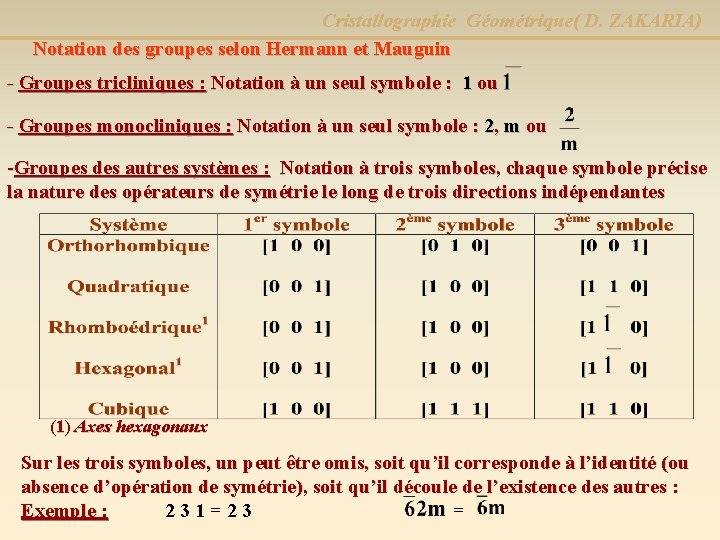
Cristallographie Géométrique( D. ZAKARIA) Notation des groupes selon Hermann et Mauguin - Groupes tricliniques : Notation à un seul symbole : 1 ou - Groupes monocliniques : Notation à un seul symbole : 2, m ou -Groupes des autres systèmes : Notation à trois symboles, chaque symbole précise la nature des opérateurs de symétrie le long de trois directions indépendantes (1) Axes hexagonaux Sur les trois symboles, un peut être omis, soit qu’il corresponde à l’identité (ou absence d’opération de symétrie), soit qu’il découle de l’existence des autres : Exemple : 2 3 1 = 2 3 =

Cristallographie Géométrique( D. ZAKARIA) Les 32 groupes ponctuels de symétrie N. B. : la symétrie d’un cristal (réseau de motifs) est au maximum celle de son réseau ponctuel. 32 classes cristallines Classes holoèdres Classes de Laüe

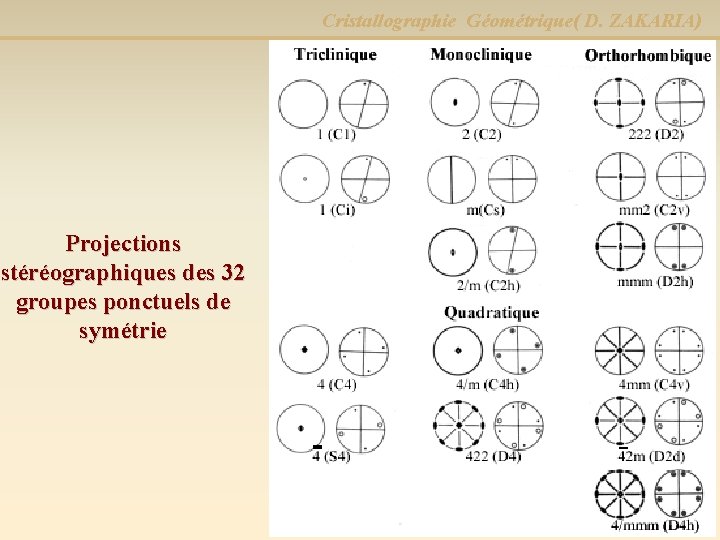
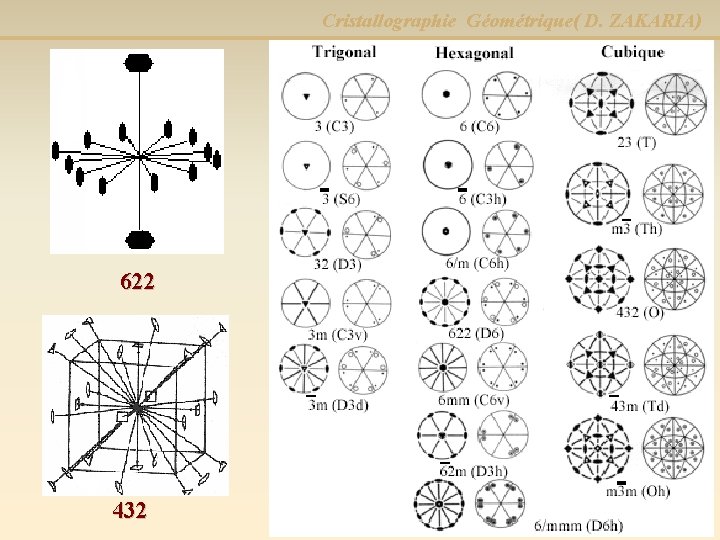
Cristallographie Géométrique( D. ZAKARIA) Projections stéréographiques des 32 groupes ponctuels de symétrie

Cristallographie Géométrique( D. ZAKARIA) 622 432

Cristallographie Géométrique( D. ZAKARIA) Indices hexagonaux de Miller-Braver Axe 6 (1 1 0 0) z (1 1 0) Les 6 faces verticales sont équivalentes car elles se déduisent les unes des autres par un axe de symétrie d’ordre 6. Deux plans sont dits équivalents si on passe de l’un à l’autre par permutation de leurs indices de Miller y x (1 0 0) (1 0 1 0) Dans un repère hexagonal, les indices de Miller classiques (1 1 0) et (1 0 0 ) ne sont pas équivalents !! ? ? Introduction d’un quatrième indice de Miller i pour le système hexagonal avec i = - (h + k) (h k l) (h k i l) Les plans (1 0 1 0) et (1 1 0 0) sont équivalents