Graph Algorithms for Planning and Partitioning Shuchi Chawla

Graph Algorithms for Planning and Partitioning Shuchi Chawla Carnegie Mellon University Thesis Oral 6/22/06 Shuchi Chawla

Planning & Partitioning problems in graphs • Find structure in a set of objects given pairwise constraints or relations on the objects • NP-hard • Our objective: study the approximability of these problems 2 Planning and Partitioning Algorithms Shuchi Chawla

Path-Planning Shuchi Chawla

A repair-bot problem • Robot receives requests for repair • Requests come with a time-window for servicing • Brownie points for each request serviced • Cannot perform all of them – Takes time to service each request – Takes time to move from one location to another • The problem: – Which ones to accept? Selection – How to schedule them? Ordering – Goal: Maximize the total brownie points 4 Planning and Partitioning Algorithms Shuchi Chawla

Path-planning • Informally… planning and ordering of tasks • Classic instance ― Traveling Salesman Problem Find the shortest tour covering all given locations • A natural extension ― Orienteering Cover as many locations as possible by a given deadline • Many variants, applications: – Delivery & distribution problems – Production planning, Supply chain management – Robot navigation • Studied in Operations Research for 2 -3 decades • Mostly NP-hard; we look for approximation algorithms 5 Planning and Partitioning Algorithms Shuchi Chawla

Approximation Results • A reward vs. time trade-off • A budget on time; maximize reward – Orienteering – Deadline-TSP – TSP with Time-Windows single deadline on time different deadlines on different locations different time windows for diff. locations • A quota on reward; minimize time – TSP – k-TSP visit all locations visit k locations • Optimize a combination of reward and time – Prize-Collecting TSP – Discounted-Reward TSP 6 minimize time plus reward foregone max. reward, reward decreases with time Planning and Partitioning Algorithms Shuchi Chawla

Approximation Results Joint work with Bansal, Blum, Karger, Meyerson, Minkoff & Lane • A reward vs. time trade-off • A budget on time; maximize reward – Orienteering – Deadline-TSP – TSP with Time-Windows ? 3 ? log n 3 ? log 2 n 3 • A quota on reward; minimize time – TSP – k-TSP Use structural properties & Dynamic Programming Use LP-rounding 1. 5 [Christofides ’ 76] 2+ [BRV 99] [Garg 99] [AK 00] [CGRT 03] … • Optimize a combination of reward and time – Prize-Collecting TSP – Discounted-Reward TSP 7 2 [Goemans Williamson ’ 92] ? 6. 75+ Planning and Partitioning Algorithms Shuchi Chawla

Why LPs don’t work • Budget problems are ill-behaved w. r. t. small perturbations • Algorithms for “quota” problems rely on the Goemans. Williamson primal-dual subroutine – Miss out on far-away reward Bad case: low slack • We can approximate the very-low slack case: – When the solution visits all nodes in order of increasing distance from start – Use dynamic program 8 Planning and Partitioning Algorithms Shuchi Chawla

Approximation Results Joint work with Bansal, Blum, Karger, Meyerson, Minkoff & Lane • A budget on time; maximize reward – Orienteering – Deadline-TSP – TSP with Time-Windows 3 3 log n 3 log 2 n • A quota on reward; minimize time – TSP – k-TSP – Min-Excess M Use structural properties & Dynamic Programming Use LP-rounding 1. 5 [Christofides ’ 76] 2+ [BRV 99] [Garg 99] [AK 00] [CGRT 03] … 2+ visit k locations, but minimize excess • Optimize a combination of reward and time – Prize-Collecting TSP – Discounted-Reward TSP with Time-Windows 9 2 [Goemans Williamson ’ 92] 6. 75+ O(c) for reward; (1+2 -c) for deadlines Planning and Partitioning Algorithms Shuchi Chawla

Stochastic planning • Robots face uncertainty – may run out of battery power – may face unforeseen obstacle causing delay – may follow instructions imprecisely • Uncertainty arises from robot’s environment, as well as its own actions • Goal: perform as many tasks as possible in expectation before failure occurs; perform all tasks as fast as possible in expectation 10 Planning and Partitioning Algorithms Shuchi Chawla

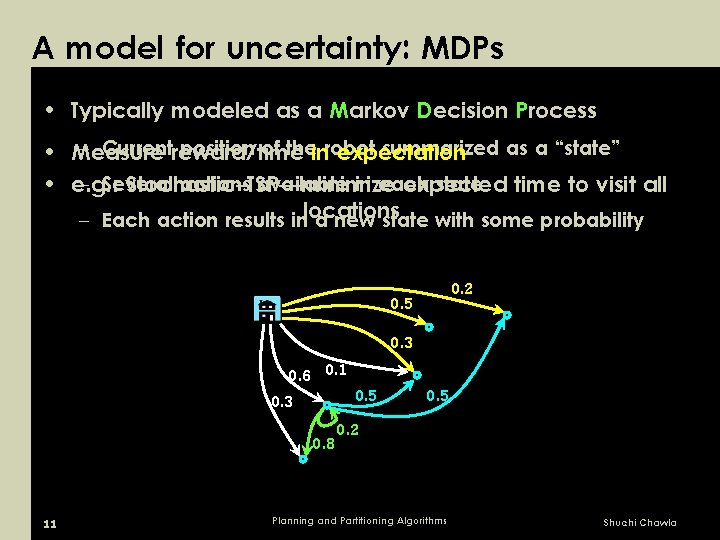
A model for uncertainty: MDPs • Typically modeled as a Markov Decision Process – Currentreward/time position of theinrobot summarized as a “state” • Measure expectation – Several actions available in each state • e. g. : Stochastic-TSP—minimize expected time to visit all – Each action results inlocations a new state with some probability 0. 2 0. 5 0. 3 0. 6 0. 1 0. 3 0. 8 11 0. 5 0. 2 Planning and Partitioning Algorithms Shuchi Chawla

Stochastic TSP • The best strategy may be dynamic – May depend on the set of states visited, number of steps taken so far … – May be exponentially long, and take exponential bits to describe • Is Stoch-TSP in NP? In PSPACE? • Can we approximate it well in poly time? • Are we allowed to compute the strategy at run-time? Two approaches: heads move forward; start again – Pre-compute in poly-time and express intails poly-bits – Iteratively compute every action at run-time in poly-time Need n heads in a row to reach the last node 2 n tries Stoch-TSP can be “iteratively”-computed in PSPACE 12 Planning and Partitioning Algorithms Shuchi Chawla

A simple solution concept: Static policies Dynamic strategy Static policy “history-dependent”: depends on previously visited states, current time, etc. … “memoryless”: depends only on current state, not on history Difficult to implement Very easy to implement, easier to analyze, better understood Poorly understood May be far from optimal What is the worst gap between Dyn and Stat? Dyn takes 2 n steps Stat takes O(n 2) 13 Planning and Partitioning Algorithms Shuchi Chawla

The adaptivity gap • What is the worst gap between Dyn and Stat? • First studied for the “stochastic-knapsack problem” – Known to be a constant [DGV’ 04, DGV’ 05] • At least (n) even in “deterministic” graphs • At most O(n log n) in deterministic graphs • At most O(n 3 log n) in general Dyn takes 2 n steps Stat takes O(n 2) 14 Planning and Partitioning Algorithms Shuchi Chawla

The adaptivity gap • The policy: – Visit every action with the “probability” that OPT visits it Is this well defined? For any set S, prob of taking an edge from S to VS 1/OPT an edge from S to VS with prob. mass 1/(n 2 OPT) For any u & v, a path of length at most n, with 3 log“probability edges. O(n having mass” at least 1/(n 2 OPT) • At most n) in general For any u & v, “hitting time” from u to v O(n 3 OPT) Adaptivity gap = O(n 3 log n) 15 Planning and Partitioning Algorithms Shuchi Chawla

A summary of our results Joint work with Blum, Kleinberg & Mc. Mahan • The optimal strategy for Stoch-TSP can be iteratively computed in PSPACE • Adaptivity gap for deterministic graphs is O(n log n) and (n) • Adaptivity gap in general = O(n 3 log n) • O(n 3 log n)-approximation using static strategies • O(n)-approximation using dynamic strategies 16 Planning and Partitioning Algorithms Shuchi Chawla

Open Problems • Approximations for directed path-planning – Chekuri, Pal give quasi-polytime polylog-approximations • Techniques for approximating planning problems on MDPs • Hardness for directed/undirected problems 17 Planning and Partitioning Algorithms Shuchi Chawla

Graph Partitioning Shuchi Chawla

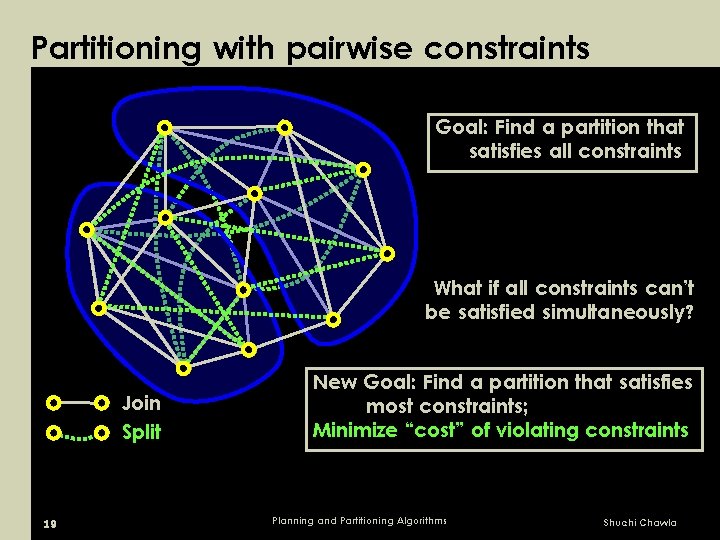
Partitioning with pairwise constraints Goal: Find a partition that satisfies all constraints What if all constraints can’t be satisfied simultaneously? Join Split 19 New Goal: Find a partition that satisfies most constraints; Minimize “cost” of violating constraints Planning and Partitioning Algorithms Shuchi Chawla

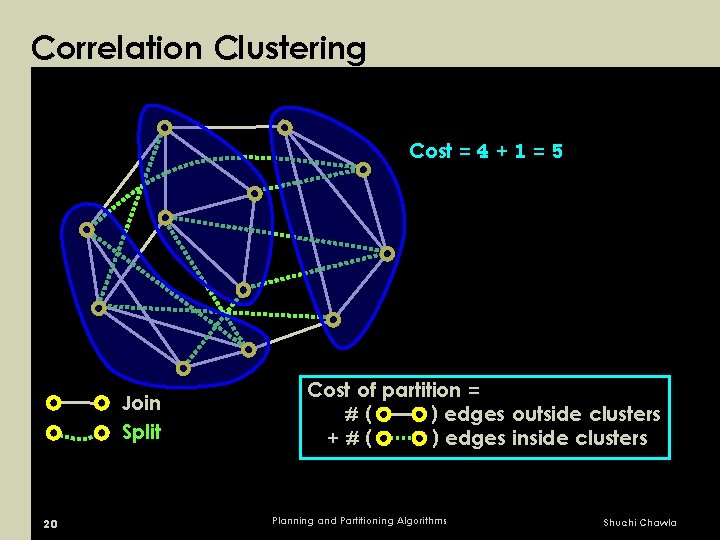
Correlation Clustering Cost = 4 + 1 = 5 Join Split 20 Cost of partition = #( ) edges outside clusters +#( ) edges inside clusters Planning and Partitioning Algorithms Shuchi Chawla

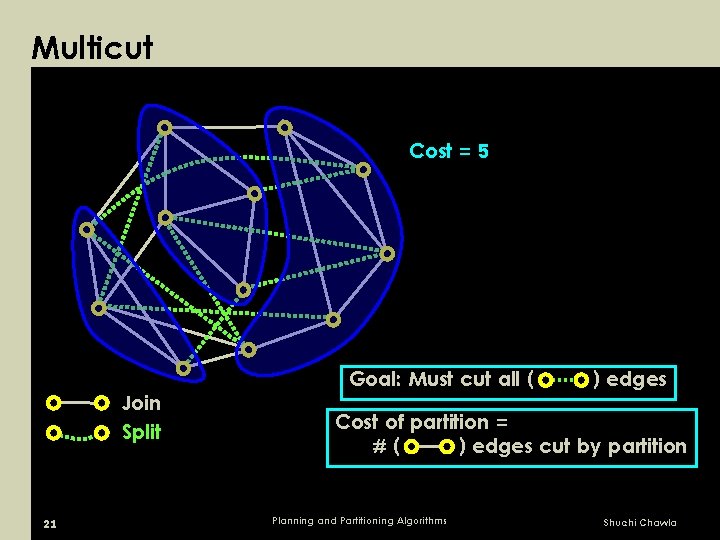
Multicut Cost = 5 Join Split 21 Goal: Must cut all ( ) edges Cost of partition = #( ) edges cut by partition Planning and Partitioning Algorithms Shuchi Chawla

Sparsest Cut Sparsity = 2/5 = 0. 4 For a set S, “demand” D(S) =#( ) edges cut “capacity” C(S) =#( )edges cut Join Split 22 Cost, or, Sparsity = C(S)/D(S) Goal: find the cut minimizing sparsity Planning and Partitioning Algorithms Shuchi Chawla

Why Partition? • Partitioning problems arise in machine learning, computational geometry, computational biology, divide -and-conquer algorithms, network design … • Correlation clustering: NLP—correference analysis, document classification, image classification, authorship disambiguation • Multicut, Sparsest Cut: divide & conquer, mixing of Markov chains, VLSI layout, graph bisection, lowdistortion metric embeddings 23 Planning and Partitioning Algorithms Shuchi Chawla

Approximating Correlation Clustering Fixed # General graph clusters Unweighted complete graph Minimizing disagreements Maximizing Correlation 24 17433 O(1) 4 3 [BBC 02] [CGW 03] [ACN 05] O(log n) ~ [CGW 03, EF 03, DI 03] APX-hard [CGW 03] APX-hard 29/28 [BBC 02] 1. 3048 1. 3044 [CGW 03] [Swamy 04] 1. 0087 [CGW 03] PTAS — O(log n) Planning and Partitioning Algorithms PTAS [GG 05] [BBC 02] [CGW 03] [CW 04] Shuchi Chawla

Approximating Multicut & Sparsest Cut O(log n) approx via LPs Multicut APX-hard Integrality gap of Q(log n) for LP & SDP (1), (log log n) based on UGC O(log n) for “uniform” demands O(log n) via LPs Sparsest Cut [DJPSY’ 94] [ACMM’ 05] [CKKRS’ 05] [LR’ 88] [LLR’ 95, AR’ 98] O( log n) for uniform demands via SDP [ARV’ 04] O( log 3/4 n ) [CGR’ 05] O( log n ) 25 [GVY’ 96] [ALN’ 05] (1), (log log n) based on UGC Nothing known! [CKKRS’ 05] Planning and Partitioning Algorithms Shuchi Chawla

Coming up… • An O(log 3/4 n)-approx for generalized Sparsest Cut • Hardness of approximation for Multicut & Sparsest Cut • Conclusions and open problems 26 Planning and Partitioning Algorithms Shuchi Chawla

Sparsest Cut and metric embeddings • Sparsity of a cut S V, (S) = (S)c(e) x S, y S D(x, y) • Given set S, define a “cut” metric S(x, y) = 1 if x and y on different sides of cut (S, V-S) 0 otherwise • (S) = e c(e) S(e) x, y D(x, y) S(x, y) ( ) = e c(e) x, y D(x, y) • Finding sparsest cut minimizing above function over all cut ℓ 1 metrics 27 Planning and Partitioning Algorithms Shuchi Chawla

Sparsest Cut and metric embeddings • Finding sparsest cut minimizing ( ) over ( ) = ℓ 1 metrics e c(e) x, y D(x, y) • Lemma: Minimize over a class ℳ to obtain NP-hard + have -distortion embedding from into -approx for sparsest cut ℓ 1 • When ℳ = all metrics, obtain O(log n) approximation [Linial London Rabinovich ’ 95, Aumann Rabani ’ 98] • Cannot do any better [Leighton Rao ’ 88] 28 Planning and Partitioning Algorithms Shuchi Chawla

Sparsest Cut and metric embeddings • Finding sparsest cut minimizing ( ) over ( ) = ℓ 1 metrics e c(e) x, y D(x, y) • Lemma: Minimize over a class ℳ to obtain Squared-Euclidean, + have -avg-distortion embedding from into ℓ 1 2 or ℓ 2 -metrics -approx for “uniform-demands” sparsest cut • ℳ = “negative-type” metrics O( log n) approx [Arora Rao Vazirani ’ 04] • Question: Can we obtain O( log n) for generalized sparsest cut, or an O( log n) distortion embedding from ℓ 22 into ℓ 1 29 Planning and Partitioning Algorithms Shuchi Chawla

Arora et al. ’s O( log n)-approx • Solve an SDP relaxation to get the best • Key Theorem: ℓ 2 2 representation 2 2 Let be a “well-spread-out” ℓ metric. Then – an embedding from into a line, such that, - for all pairs (x, y), (x, y) For a(x, y) const. fraction of (x, y), (x, y) > const. 1⁄ - for a constant fraction of (x, y), (x, y) O( log n) (x, y) diameter • The general case Implies – issuesan avg. distortion of O( log 1. Well-spreading does not hold n) 2. Constant fraction is not enough Want low distortion for every demand pair. 30 Planning and Partitioning Algorithms Shuchi Chawla

1. Ensuring well-spreading • Divide pairs into groups based on distances Di = { (x, y) : 2 i (x, y) 2 i+1 } • At most O(log n) groups • Each group by itself is well-spread, by definition • Embed each group individually – distortion O( log n) contracting embedding into a line for each (assume for now) • “Glue” the embeddings appropriately – Naïve gluing via concatenation: distortion O( log n) = O(log n) – A better gluing: “measured-descent” by Krauthgamer et al. ’ 04 gives distortion O( log n) = O( log¾ n ) 31 Planning and Partitioning Algorithms Shuchi Chawla

2. Average to worst-case distortion • Arora et al. ’s guarantee – a constant fraction of pairs embed with low distortion • We want – every pair should embed with low distortion • Idea: Re-embed pairs that have high distortion • Problem: Increases the number of embeddings, implying a larger distortion • A “re-weighting” solution: – Don’t ignore low-distortion pairs completely – keep them around and reduce their importance 32 Planning and Partitioning Algorithms Shuchi Chawla

Summarizing… Joint work with Gupta & Räcke • Start with a solution to the SDP • For every distance scale – Use [ARV 04] to embed points into line – Use re-weighting to obtain good worst-case distortion • Combine distance scales using measured-descent • In practice – Write another SDP to find best embedding into ℓ 2 – Use J-L to embed ℓ 2 into ℓ 1 and then into a cut-metric 33 Planning and Partitioning Algorithms Shuchi Chawla

Coming up… • An O(log 3/4 n)-approx for generalized Sparsest Cut • Hardness of approximation for Multicut & Sparsest Cut • Conclusions and open problems 34 Planning and Partitioning Algorithms Shuchi Chawla

Hardness of approximation: our results Joint work with Krauthgamer, Kumar, Rabani & Sivakumar • Use Khot’s Unique Games Conjecture (UGC) – A certain label cover problem is NP-hard to approximate The following holds for Multicut, Sparsest Cut and Min-2 CNF Deletion : • UGC L-hardness for any constant L > 0 • Stronger UGC (log log n)-hardness 35 Planning and Partitioning Algorithms Shuchi Chawla

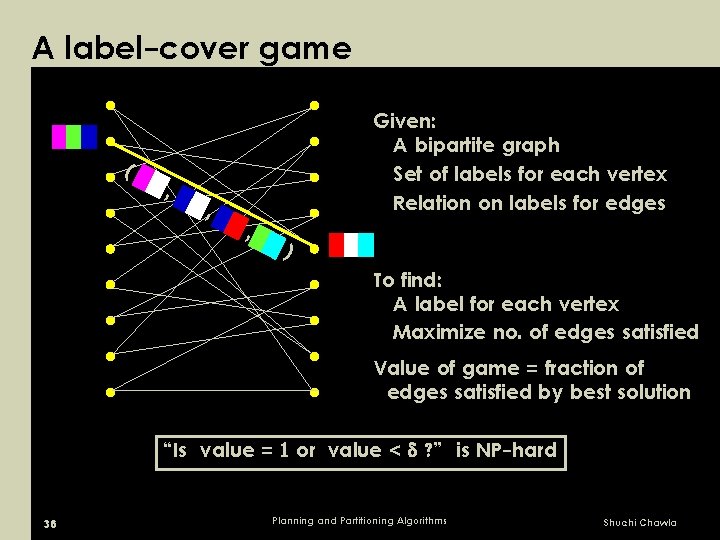
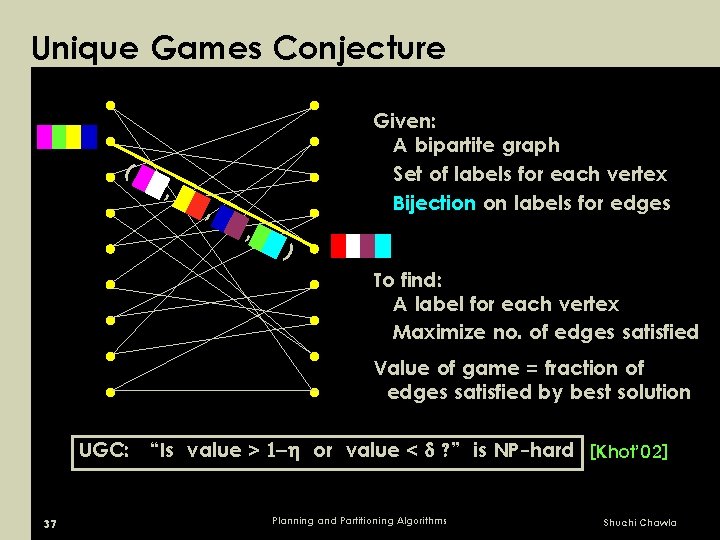
A label-cover game ( , , Given: A bipartite graph Set of labels for each vertex Relation on labels for edges , ) To find: A label for each vertex Maximize no. of edges satisfied Value of game = fraction of edges satisfied by best solution “Is value = or value < ? ” is NP-hard 36 Planning and Partitioning Algorithms Shuchi Chawla

Unique Games Conjecture ( , , Given: A bipartite graph Set of labels for each vertex Bijection on labels for edges , ) To find: A label for each vertex Maximize no. of edges satisfied Value of game = fraction of edges satisfied by best solution UGC: “Is value > or value < ? ” is NP-hard [Khot’ 02] 37 Planning and Partitioning Algorithms Shuchi Chawla

The power of UGC • Implies the following hardness results – Vertex-Cover 2 – Max-cut GW = 0. 878 [KR’ 03] [KKMO’ 04] – Min 2 -CNF Deletion – Max-k-cut – 2 -Lin-mod-2. . . UGC: “Is value > or value < ? ” is NP-hard [Khot’ 02] 38 Planning and Partitioning Algorithms Shuchi Chawla

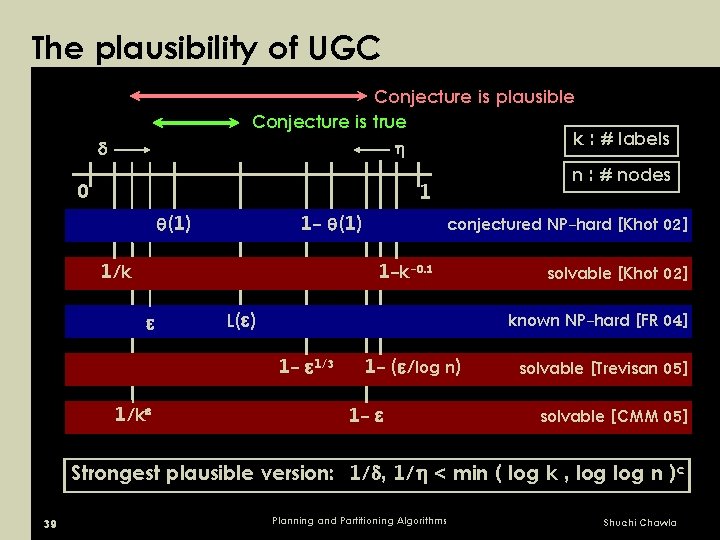
The plausibility of UGC Conjecture is plausible Conjecture is true k : # labels n : # nodes 1 0 1 - (1) 1/k conjectured NP-hard [Khot 02] 1 -k-0. 1 L( ) known NP-hard [FR 04] 1 - 1/3 1/k solvable [Khot 02] 1 - ( /log n) 1 - solvable [Trevisan 05] solvable [CMM 05] Strongest plausible version: 1/ , 1/ < min ( log k , log n )c 39 Planning and Partitioning Algorithms Shuchi Chawla

Our results • Use Khot’s Unique Games Conjecture (UGC) – A certain label cover problem is hard to approximate The following holds for Multicut, Sparsest Cut and Min-2 CNF Deletion : • UGC ( log 1/( + ) )-hardness L-hardness for any constant L > 0 • Stronger UGC ( log log n )-hardness ( k log n, , (log n)-c ) 40 Planning and Partitioning Algorithms Shuchi Chawla

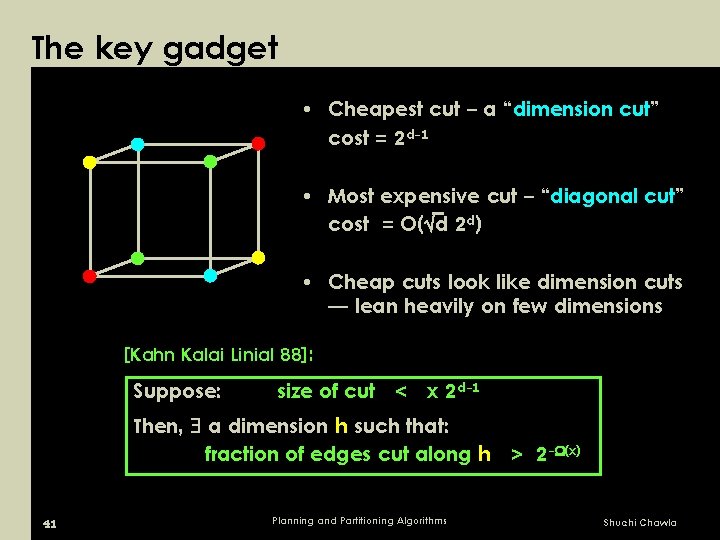
The key gadget • Cheapest cut – a “dimension cut” cost = 2 d-1 • Most expensive cut – “diagonal cut” cost = O( d 2 d) • Cheap cuts look like dimension cuts — lean heavily on few dimensions [Kahn Kalai Linial 88]: Suppose: size of cut < x 2 d-1 Then, a dimension h such that: fraction of edges cut along h > 2 - (x) 41 Planning and Partitioning Algorithms Shuchi Chawla

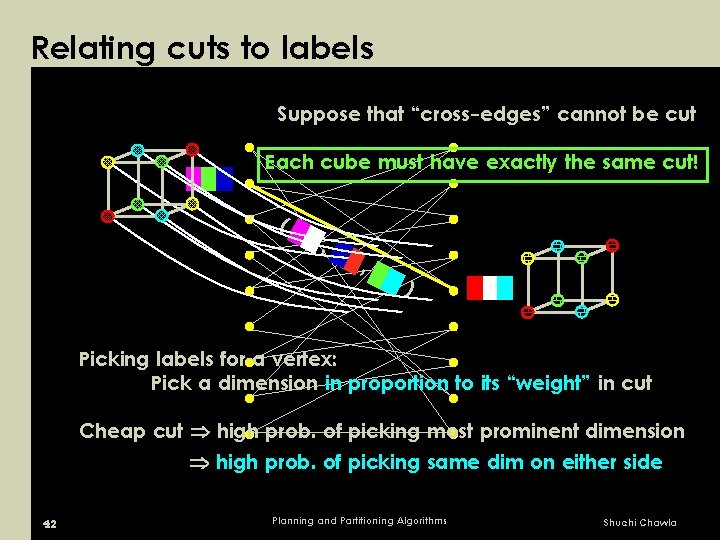
Relating cuts to labels Suppose that “cross-edges” cannot be cut Each cube must have exactly the same cut! ( , , ) Picking labels for a vertex: Pick a dimension in proportion to its “weight” in cut Cheap cut high prob. of picking most prominent dimension high prob. of picking same dim on either side 42 Planning and Partitioning Algorithms Shuchi Chawla

A recap… cut > log 1/( + ) 2 d-1 per cube cut < 2 d per cube “NO”-instance of UG “YES”-instance of UG UGC: NP-hard to distinguish between “YES” and “NO” instances of UG NP-hard to distinguish between whether cut < 2 dn or cut > log 1/( + ) 2 d-1 n ( log 1/( + ) )-hardness for Multicut 43 Planning and Partitioning Algorithms Shuchi Chawla

A related result… [Khot Vishnoi 05] • Independently obtain ( min (1/ , log 1/ )1/6 ) hardness based on the same assumption • Use this to develop an “integrality-gap” instance for the Sparsest Cut SDP – A graph with low SDP value and high actual value – Implies that we cannot obtain a better than O(log n)1/6 approximation using SDPs – Independent of any assumptions! 44 Planning and Partitioning Algorithms Shuchi Chawla

Open Problems • Closing the gap for Sparsest cut – Better approximation via SDP? Would have to avoid embedding via ℓ 2 – Improving the hardness — Fourier analysis is tight – Reduction based on a general 2 -prover system • Prove/disprove UGC • Hardness for uniform sparsest cut, min-bisection, cuts in directed graphs, … ? 45 Planning and Partitioning Algorithms Shuchi Chawla