Line Segments Distance and Midpoint Partitioning a Segment

Line Segments, Distance and Midpoint Partitioning a Segment CC Standard G-GPE. 6 Find the point on a directed line segment between two given points that partitions the segment in a given ratio. At the end of this lesson, you should be able to answer the following question: How do you find the point on a directed line segment that partitions the segment in a given ratio?

Point P divides in the ratio 3 to 1. 1. What does this mean?

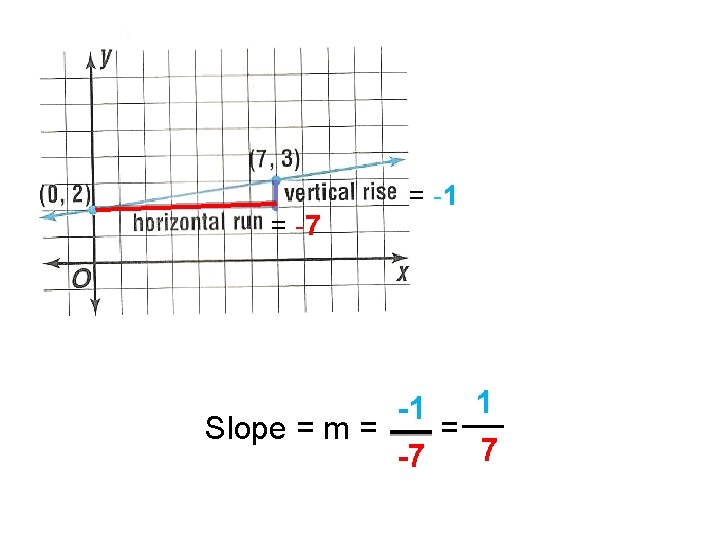
= -7 = -1 1 -1 Slope = m = = 7 -7

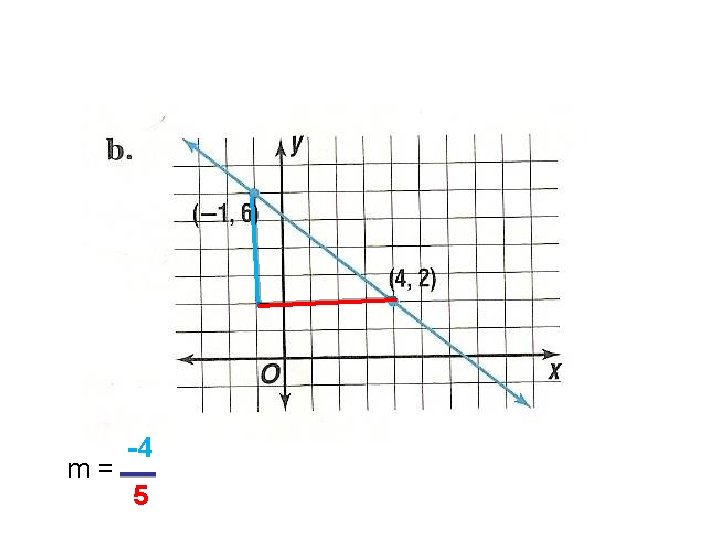
m= -4 5

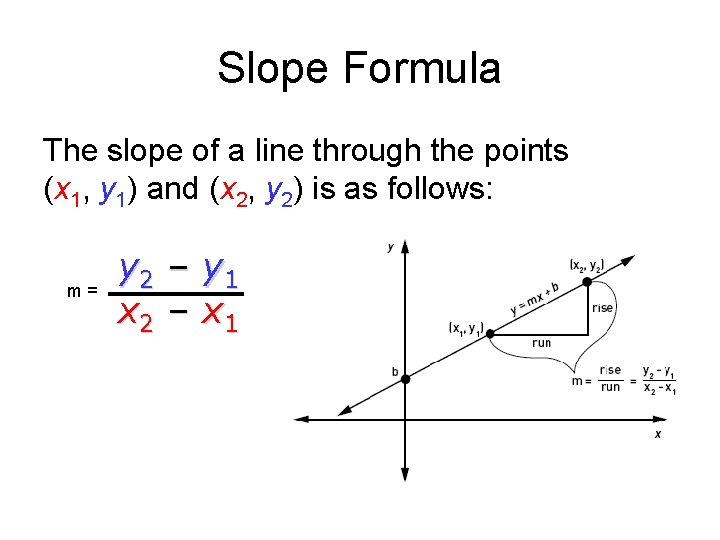
Slope Formula The slope of a line through the points (x 1, y 1) and (x 2, y 2) is as follows: m= y 2 x 2 – – y 1 x 1

Ex. Find the slope of the line that passes through (– 2, – 3) and (4, 6). Let (x 1, y 1) be (– 2, – 3) and (x 2, y 2) be (4, 6). y 2 – y 1 6 – (– 3) Substitute 6 for y 2, – 3 for y 1, = x 2 – x 1 4 – (– 2) 4 for x 2, and – 2 for x 1. 9 3 =6 =2 The slope of the line that passes through ( – 2, – 3) and (4, 6) is 3. 2 *** Always reduce your fractions****

Example 1: Find the coordinate of point P that lies along the directed line segment from A(3, 4) to B(6, 10) and partitions the segment in the ratio of 3 to 2. Directed Line Segment: Tells the direction in which from which point to start and end. In this case, from Point A to Point B So point A must be labeled A and B What does that tell you about the distance AP and PB in relation to AB?

Partitioning a segment 1. Label your points and Note: since it is a directed segment, order does matter. 2. Convert the ratio into a percent (keep as a fraction) a: b Percent ratio (%) 3. Find the rise and run for the segment (order does matter) Rise: Run: 4. To find the partitioning point: x – coordinate: x 1 -coordinate + run(% in fraction form) y - coordinate: y 1 -coordinate + rise(% in fraction form)

Find the coordinate of point P that lies along the directed line segment from A(3, 4) to B(6, 10) and partitions the segment in the ratio of 3 to 2. 1. Label your points. (note: Since it is a directed segment, order does matter, so A(x 1, y 1) and B(x 2, y 2) ). 2. Convert the ratio into a percent 3. Find the rise and run for AB 4. The slope of AP must be the same as AB. So, to find the coordinates of P, add 60% of the run to the x-coordinate of A and add 60% of the rise to the y-coordinate of A How can you use the distance formula to check that P partitions ratio of 3 to 2? in the

Example 2: Find the coordinates of the point P that lies along the directed segment from A(1, 1) to B(7, 3) and partitions the segment in the ratio of 1 to 4

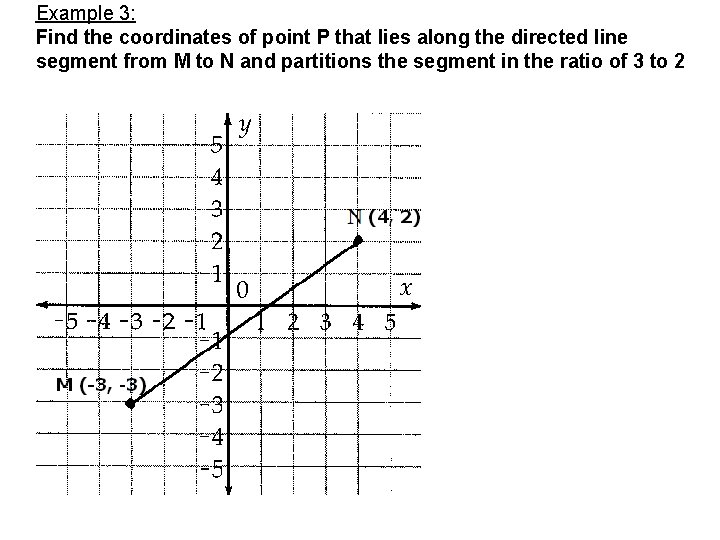
Example 3: Find the coordinates of point P that lies along the directed line segment from M to N and partitions the segment in the ratio of 3 to 2

Essential question: • How do you find the point on a directed line segment that partitions the segment in a given ratio?

• Class assignment: Partitioning a segment: Page 210: 7 -8 Worksheet: Partitioning Segments