The Distance and Midpoint Formulas Goal 1 Find








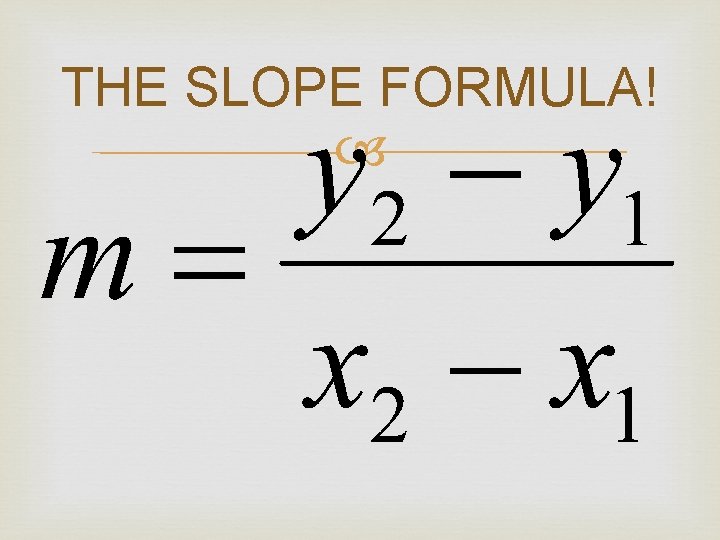


































- Slides: 58

The Distance and Midpoint Formulas Goal 1 Find the Midpoint of a Segment Goal 2 Find the distance between two points on a coordinate plane Goal 3 Find the slope of a line between two points on a coordinate plane

Distance Formula Used to find the distance between two points

Example Find the distance between (2, 1) and (5, 2). x 1 y 1 D= (2 - 5)² + (1 - 2)² D= (-3)² + (-1)² D= 9+1 D= 10 D= 3. 162 x 2 y 2 -First substitute numbers for variables and solve the parentheses. -Then solve the squared number. -Add the two numbers. -Find the square root of the remaining number.

Example Find the distance between A(4, 8) and B(1, 12) A (4, 8) B (1, 12)

YOU TRY!! Find the distance between: A. (2, 7) and (11, 9) B. (-5, 8) and (2, - 4)

Midpoint Formula Used to find the center of a line segment

Example Find the midpoint between A(4, 8) and B(1, 12) A (4, 8) B (1, 12)

YOU TRY!! Find the midpoint between: A) (2, 7) and (14, 9) B) (-5, 8) and (2, - 4)
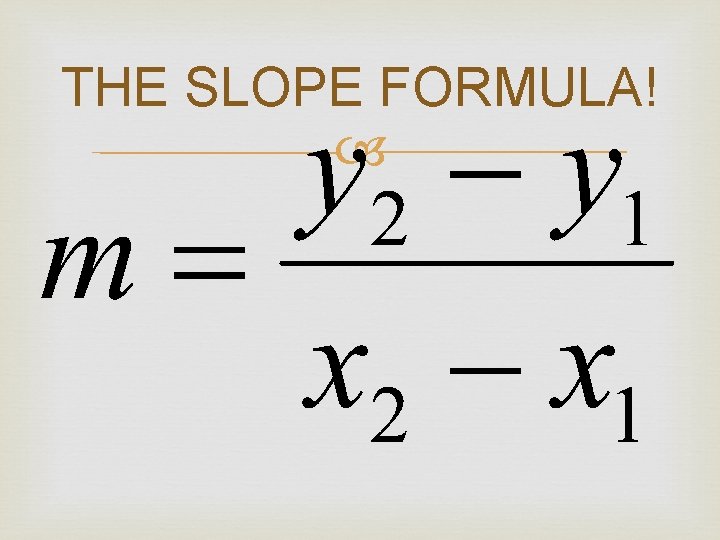
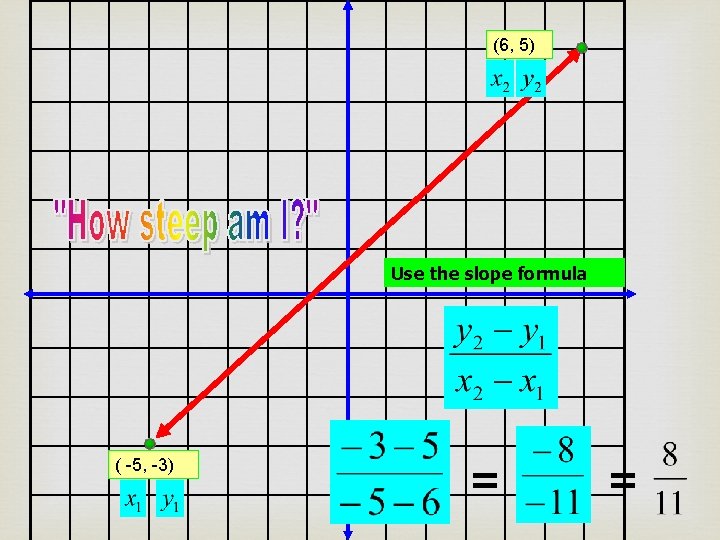
THE SLOPE FORMULA!

(6, 5) Use the slope formula ( -5, -3) = =

Homework Complete the handout given in class. It is also posted on Grade. Speed and my website.

12. 6 Midpoint and Distance Formulas Goal 1 Find the Midpoint of a Segment Goal 2 Two Find the Distance Between Points on a Coordinate Plane

The Midpoint Formula The midpoint between the two points (x 1, y 1) and (x 2, y 2) is:

Example 1 Find the midpoint of the segment whose endpoints are (6, -2) & (2, 9)

Example 2 Find the coordinates of the midpoint of the segment whose endpoints are (5, 2) and ( 7, 8)

Example 3 Find the coordinates of the midpoint of the segment whose endpoints are (-2, 8) and ( 4, 0)

Distance Formula The distance between two points with coordinates (x 1, y 1) and (x 2, y 2) is given by:

Example 4 Find the Distance Between the points. (-2, 5) and (3, -1) Let (x 1, y 1) = (-2, 5) and (x 2, y 2) = (3, -1)

Example 5 What is the distance between P(- 1, 4) and Q(2, - 3)?

Example 6 What is the distance between P(3, 0) and Q(5, - 4)?

Example 7 What is the distance between P(-5, 2) and Q(2, - 5)?

Use the distance formula to determine whether the three points are vertices of a right triangle: (1, 1), (4, 4), (4, 1) Example 8

Use the distance formula to determine whether the three points are vertices of a right triangle: (3, -4), (-2, -1), (4, 6). Example 9 p. 748 #16 -28 e, 36 -44 e, 61 -63

There are formulas that you will be provided with to calculate various pieces of information about pairs of points. Each formula refers to a set of two points: (x 1, y 1) and (x 2, y 2)

Distance – the length of the line segment that connects two given points in the coordinate plane. Distance Formula:

Ex#1: (2, 2) and (5, -2) Distance: ____

The midpoint is the point equidistant between two points in the coordinate plane. Midpoint Formula: NOTICE: the answer to a midpoint formula problem will be in the form (1, 2) – meaning your answer is another point!

Ex# 1: (2, 2) and (5, -2) Midpoint: _______

The slope is the ratio of vertical change (rise) to horizontal change (run) of a line. Slope Formula:

Ex# 1: (2, 2) and (5, -2) Slope: _____

Example 2: (0, 3) and (-1, 1) Distance: ____ Midpoint: _______ Slope: _____

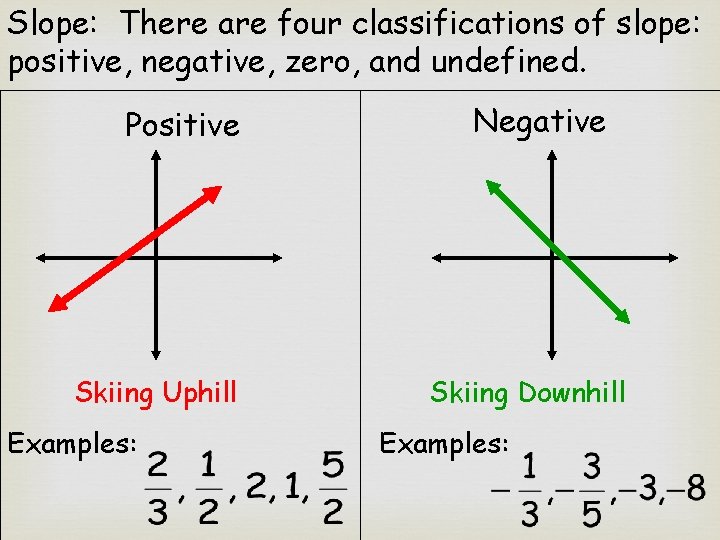
Slope: There are four classifications of slope: positive, negative, zero, and undefined. Positive Skiing Uphill Examples: Negative Skiing Downhill Examples:

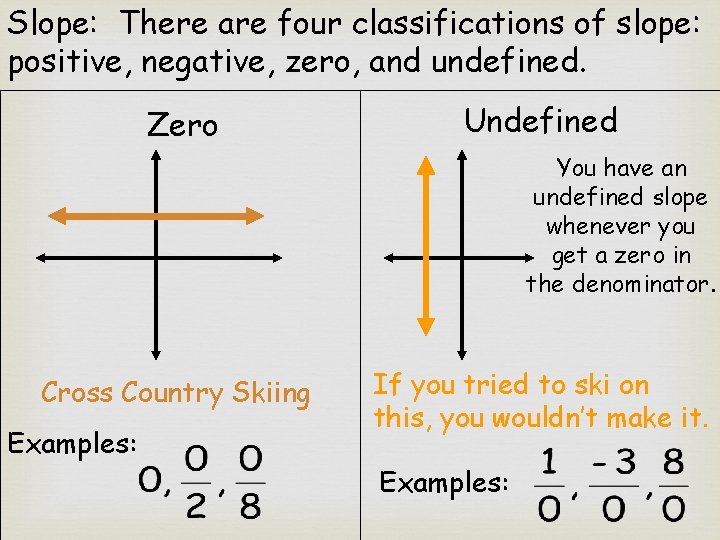
Slope: There are four classifications of slope: positive, negative, zero, and undefined. Zero Undefined You have an undefined slope whenever you get a zero in the denominator. Cross Country Skiing Examples: If you tried to ski on this, you wouldn’t make it. Examples:

Independent Practice: Calculate the slope for each pair of points. Classify each slope as positive, negative, zero, or undefined. 1. (2, 2) and (3, 5) 2. (0, 0) and (3, 0) Slope: 3 Classification: Positive Slope: 0 Classification: Zero 3. (-2, -1) and (-1, -4) 4. (2, 3) and (2, 7) Slope: -3 Classification: Negative Slope: Undefined Classification: Undefined 5. (-1, -1) and (5, 5) 6. (8, 4) and (6, 4) Slope: 1 Classification: Positive Slope: 0 Classification: Zero

Lesson 1 -3 Formulas Lesson 1 -3: Formulas 35

The Coordinate Plane plane, the horizontal number line Definition: In the coordinate (called the x- axis) and the vertical number line (called the y- axis) interest at their zero points called the Origin. y - axis Origin x - axis Lesson 1 -3: Formulas 36

The Distance Formula The distance d between any two points with coordinates and is given by the formula d = . Example: Find the distance between (-3, 2) and (4, 1) x 1 = -3, x 2 = 4, y 1 = 2 , y 2 = 1 d= d= d= Lesson 1 -3: Formulas 37

Midpoint Formula In the coordinate plane, the coordinates of the midpoint of a segment whose endpoints have coordinates and. Example: are Find the midpoint between (-2, 5) and (6, 4) x 1 = -2, x 2 = 6, y 1 = 5, and y 2 = 4 M= M= Lesson 1 -3: Formulas 38

Slope Formula Definition: In a coordinate plane, the slope of a line is the ratio of its vertical rise over its horizontal run. Formula: The slope m of a line containing two points with coordinates the formula and is given by where . Example: Find the slope between (-2, -1) and (4, 5). Lesson 1 -3: Formulas 39

Describing Lines rise from left to right. Lines that have a positive slope Lines that have a negative slope fall from left to right. Lines that have no slope (the slope is undefined) are vertical. Lines that have a slope equal to zero are horizontal. Lesson 1 -3: Formulas 40

Some More Examples Find the slope between (4, -5) and (3, -5) and describe it. m= Since the slope is zero, the line must be horizontal. l Find the slope between (3, 4) and (3, -2) and describe the line. m= Since the slope is undefined, the line must be vertical. Lesson 1 -3: Formulas 41

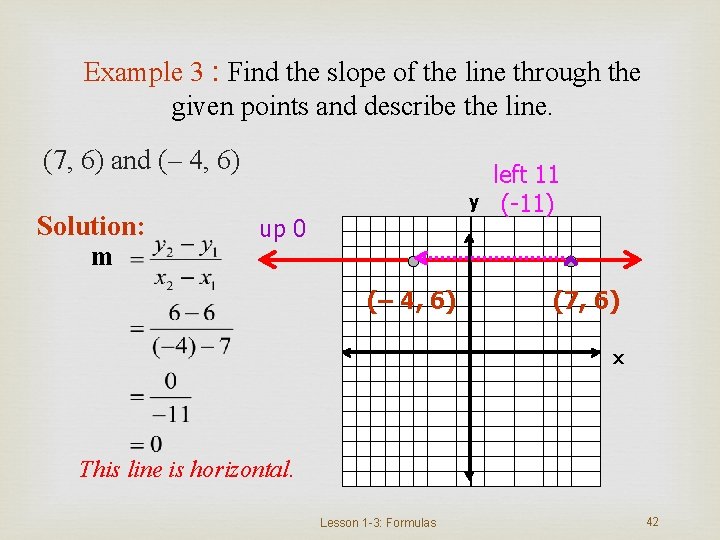
Example 3 : Find the slope of the line through the given points and describe the line. (7, 6) and (– 4, 6) Solution: m y up 0 (– 4, 6) left 11 (-11) (7, 6) x This line is horizontal. Lesson 1 -3: Formulas 42

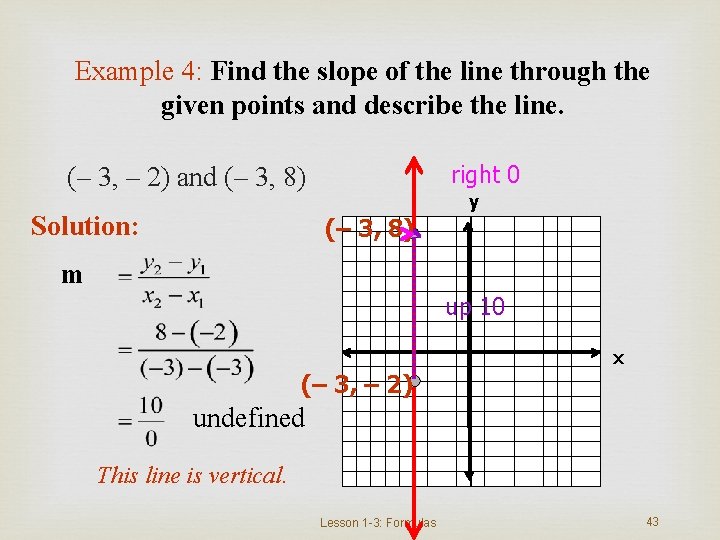
Example 4: Find the slope of the line through the given points and describe the line. right 0 (– 3, – 2) and (– 3, 8) Solution: y (– 3, 8) m up 10 x (– 3, – 2) undefined This line is vertical. Lesson 1 -3: Formulas 43

Practice l Find the distance between (3, 2) and (-1, 6). l Find the midpoint between (7, -2) and (-4, 8). l Find the slope between (-3, -1) and (5, 8) and describe the line. l Find the slope between (4, 7) and (-4, 5) and describe the line. l Find the slope between (6, 5) and (-3, 5) and describe the line. Lesson 1 -3: Formulas 44

Example 1 Use the Distance Formula Example 2 Use the Distance Formula to Solve a Problem Example 3 Use the Midpoint Formula

Find the distance between M(8, 4) and N(– 6, – 2). Round to the nearest tenth, if necessary. Use the Distance Formula Simplify.

Evaluate (– 14)2 and (– 6)2. Add 196 and 36. Take the square root. Answer: The distance between points M and N is about 15. 2 units.

Find the distance between A(– 4, 5) and B(3, – 9). Round to the nearest tenth, if necessary. Answer: The distance between points A and B is about 15. 7 units.

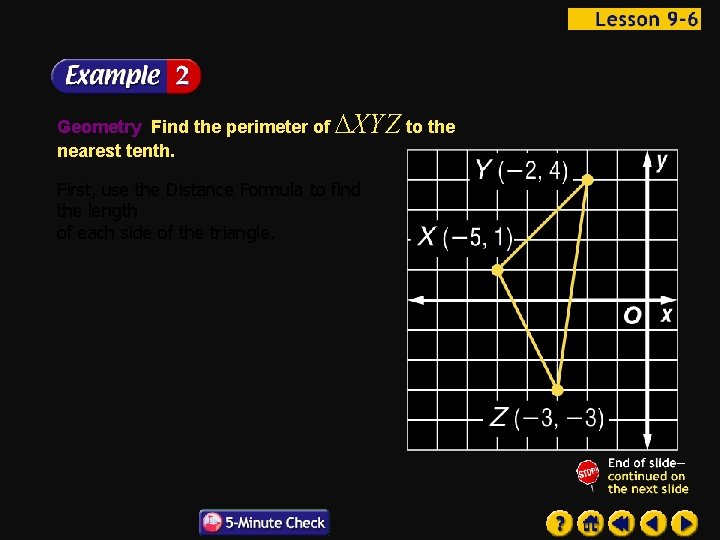
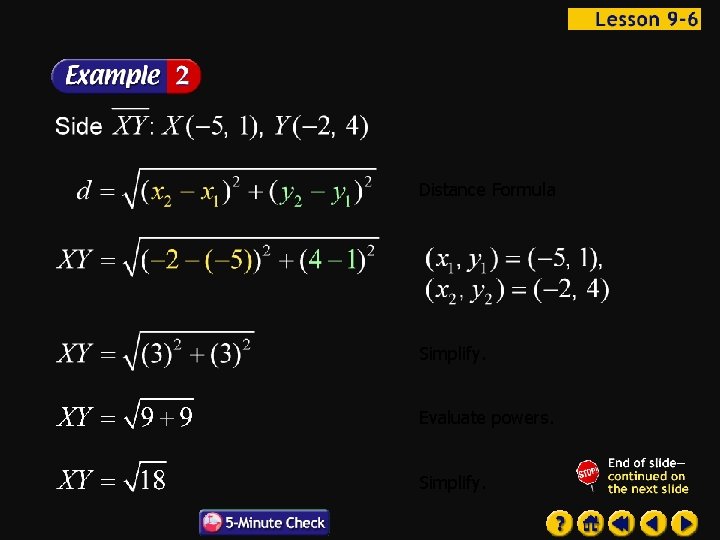
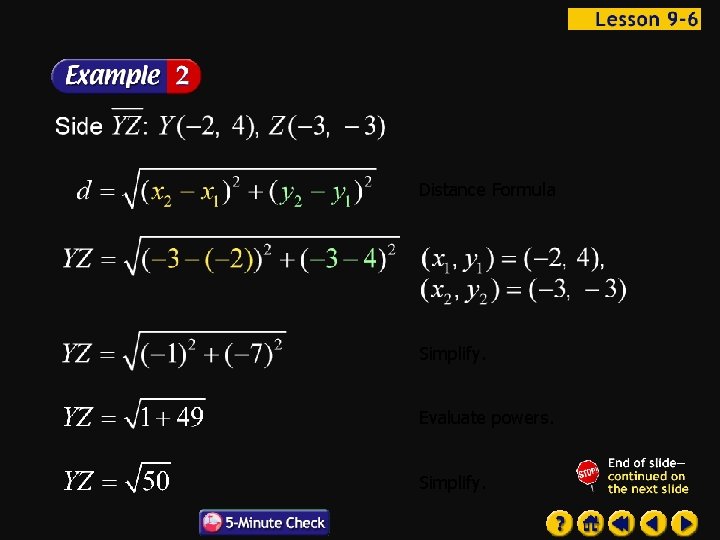
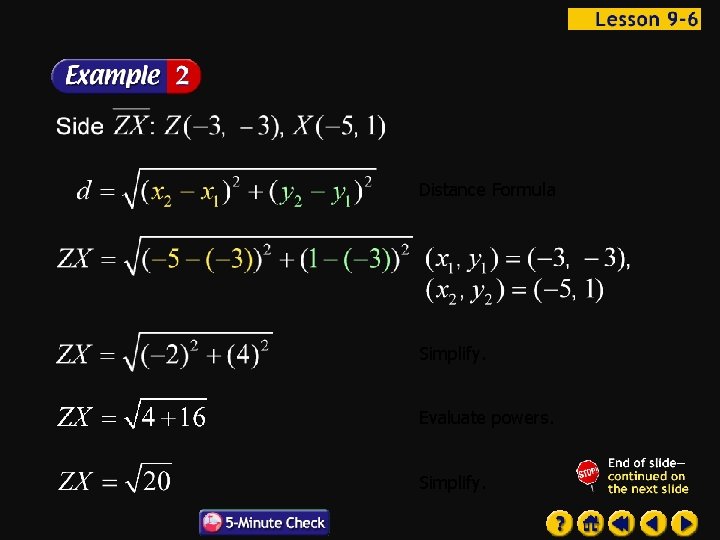
Geometry Find the perimeter of XYZ to the nearest tenth. First, use the Distance Formula to find the length of each side of the triangle.

Distance Formula Simplify. Evaluate powers. Simplify.

Distance Formula Simplify. Evaluate powers. Simplify.

Distance Formula Simplify. Evaluate powers. Simplify.

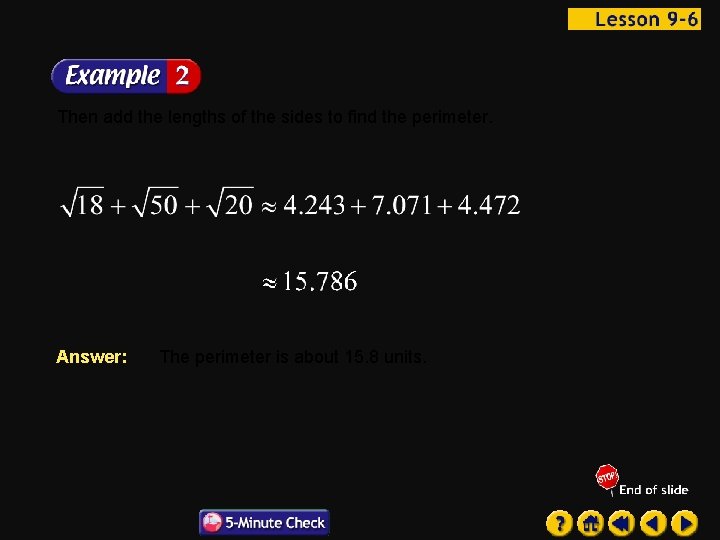
Then add the lengths of the sides to find the perimeter. Answer: The perimeter is about 15. 8 units.

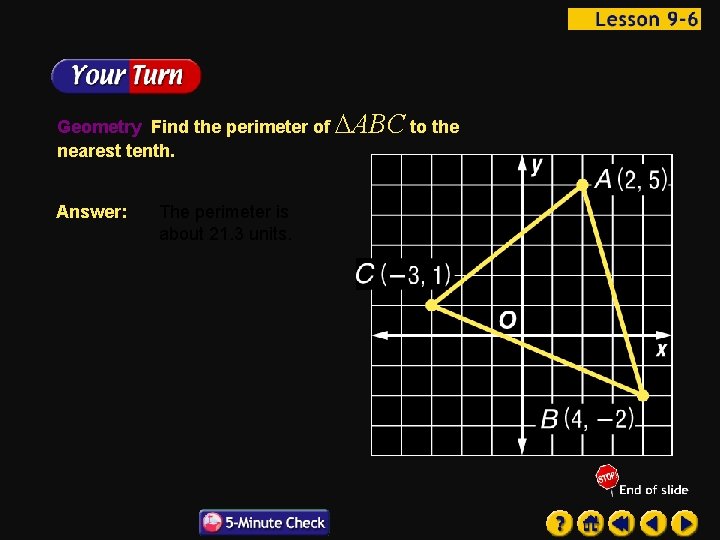
Geometry Find the perimeter of ABC to the nearest tenth. Answer: The perimeter is about 21. 3 units.

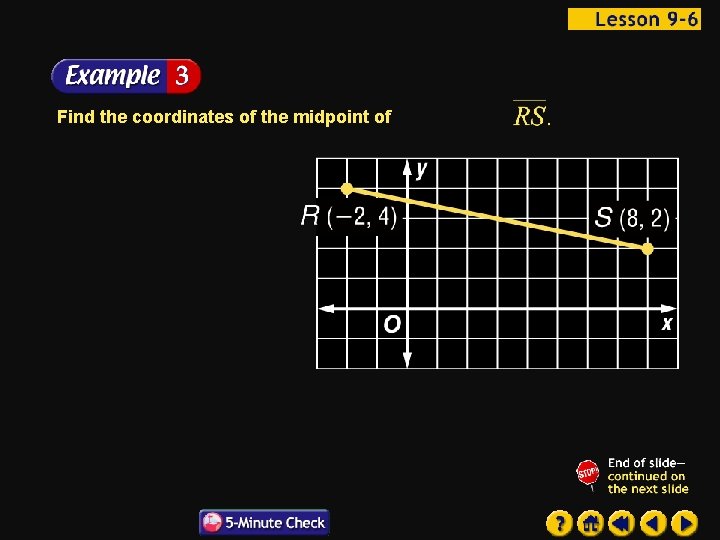
Find the coordinates of the midpoint of

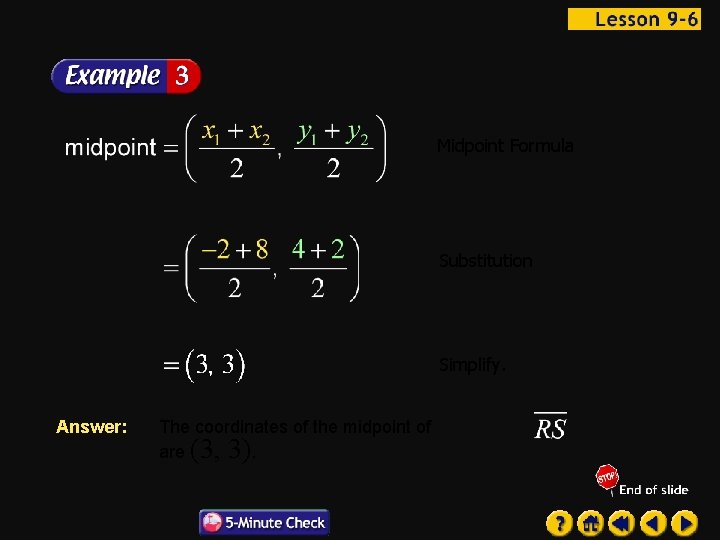
Midpoint Formula Substitution Simplify. Answer: The coordinates of the midpoint of are (3, 3).

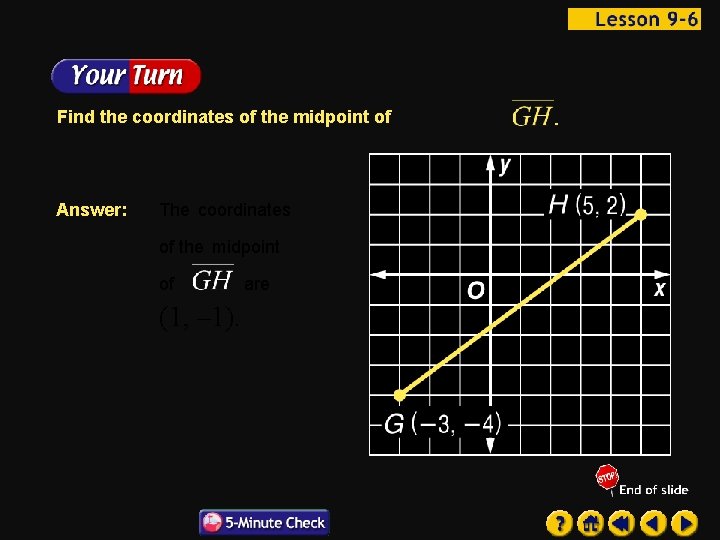
Find the coordinates of the midpoint of Answer: The coordinates of the midpoint of (1, – 1). are
