1 1 Line Segments Distance and Midpoint 1

1. 1 Line Segments, Distance and Midpoint 1. 1 d – Partitioning a Segment CC Standard G-GPE. 6 Find the point on a directed line segment between two given points that partitions the segment in a given ratio. At the end of this lesson, you should be able to answer the following question: How do you find the point on a directed line segment that partitions the segment in a given ratio?

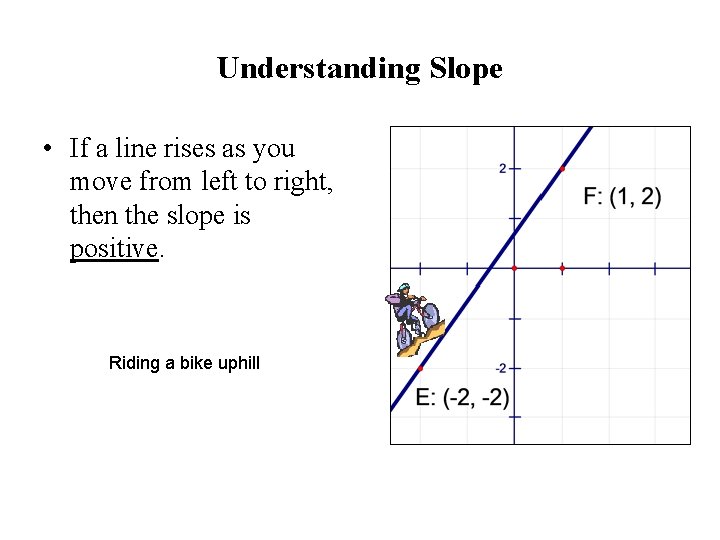
Understanding Slope • If a line rises as you move from left to right, then the slope is positive. Riding a bike uphill

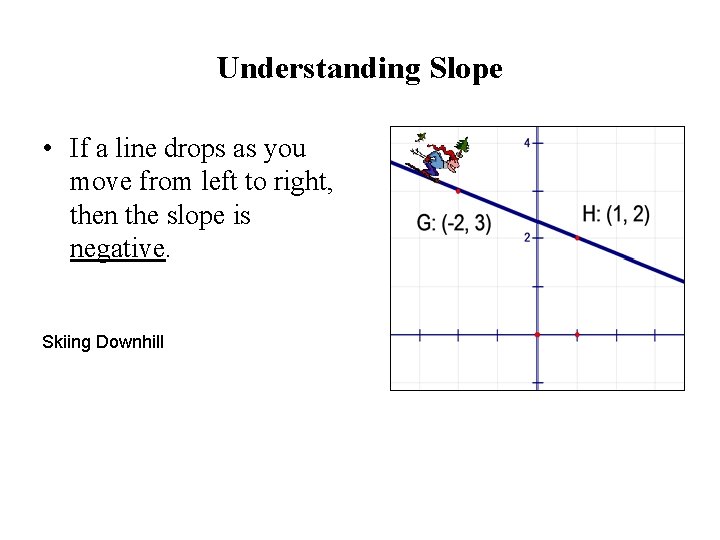
Understanding Slope • If a line drops as you move from left to right, then the slope is negative. Skiing Downhill

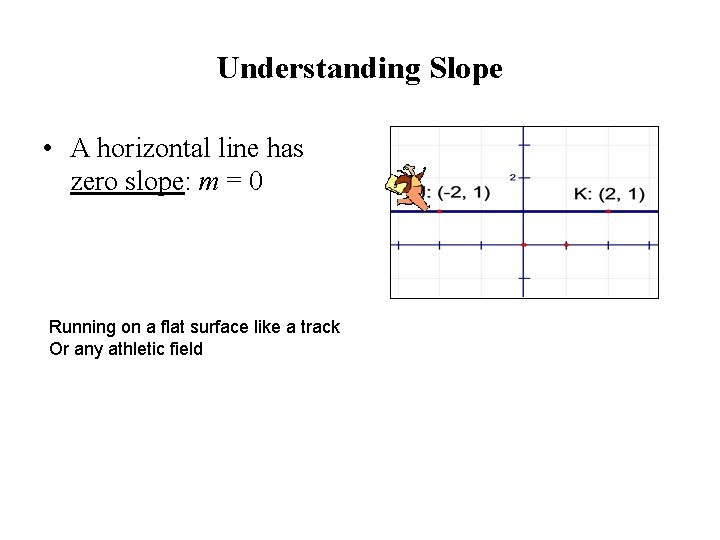
Understanding Slope • A horizontal line has zero slope: m = 0 Running on a flat surface like a track Or any athletic field

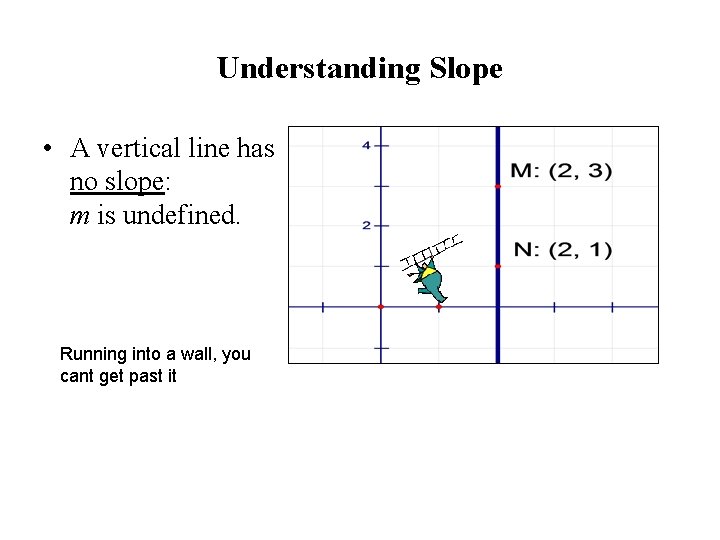
Understanding Slope • A vertical line has no slope: m is undefined. Running into a wall, you cant get past it

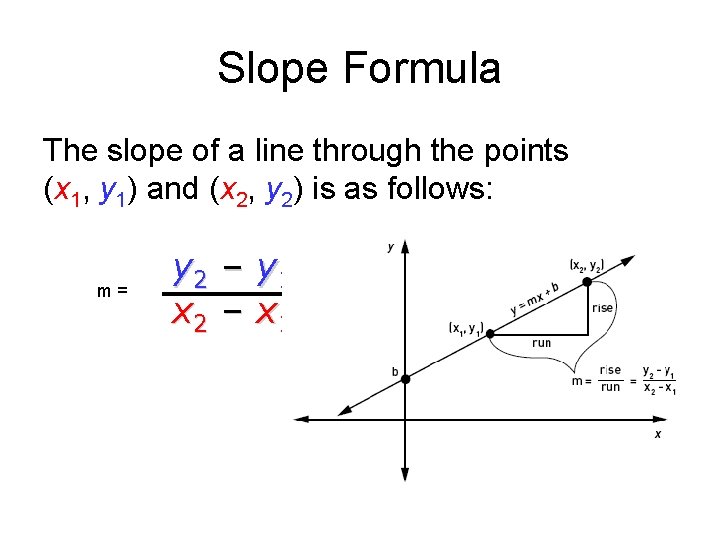
Slope Formula The slope of a line through the points (x 1, y 1) and (x 2, y 2) is as follows: m= y 2 x 2 – – y 1 x 1

Ex. Find the slope of the line that passes through (– 2, – 3) and (4, 6). Let (x 1, y 1) be (– 2, – 3) and (x 2, y 2) be (4, 6). y 2 – y 1 6 – (– 3) Substitute 6 for y 2, – 3 for y 1, = x 2 – x 1 4 – (– 2) 4 for x 2, and – 2 for x 1. 9 3 =6 =2 The slope of the line that passes through ( – 2, – 3) and (4, 6) is 3. 2 *** Always reduce your fractions****

What is a ratio? • A ratio is a comparison of two quantities • The ratio of a to b can be expressed as: a: b or a/ b or

Connor has a wallet with: 1 -$20 bill 2 - $10 bills 1 - $5 bill 8 -$1 bills 1) What is the ratio of $1 bills to $10 bills? 2) What is the ratio of $10 bills to the total number of bills in the wallet?

Point P divides in the ratio 3 to 1. 1. What does this mean?

A 32 foot long piece of rope has a knot tied to divide the rope into a ratio of 3: 5. A B 32 ft Where should the knot be tied?

Example 1: Find the coordinate of point P that lies along the directed line segment from A(3, 4) to B(6, 10) and partitions the segment in the ratio of 3 to 2. Directed Line Segment: Tells the direction in which from which point to start and end. In this case, from Point A to Point B What does that tell you about the distance AP and PB in relation to AB?

Find the coordinate of point P that lies along the directed line segment from A(3, 4) to B(6, 10) and partitions the segment in the ratio of 3 to 2. (4. 8, 7. 6) 1. Find the rise and run for AB (since you start at A and end at B, make Ax 1 and Bx 2) 2. Multiply the rise by the ratio from A to P, and the run by the ratio of A to P 3. Add/subtract these values to your starting point A 4. How can you use the distance formula to check that P partitions ratio of 3 to 2? in the

example Find the point Q along the directed line segment from point R(– 3, 3) to point S(6, – 3) that divides the segment into the ratio 2 to 1 1. Find the rise and run for RS (since you start at R and end at S, make Rx 1 and Sx 2) 2. Multiply the rise by the ratio from R to Q, and the run by the ratio of R to Q 3. Add/subtract these values to your starting point R

example Find the point Q along the directed line segment from point R(– 2, 4) to point S(18, – 6) that divides the segment in the ratio 3 to 7.

example Find the coordinates of the point P that lies along the directed segment from A(1, 1) to B(7, 3) and partitions the segment in the ratio of 1 to 4

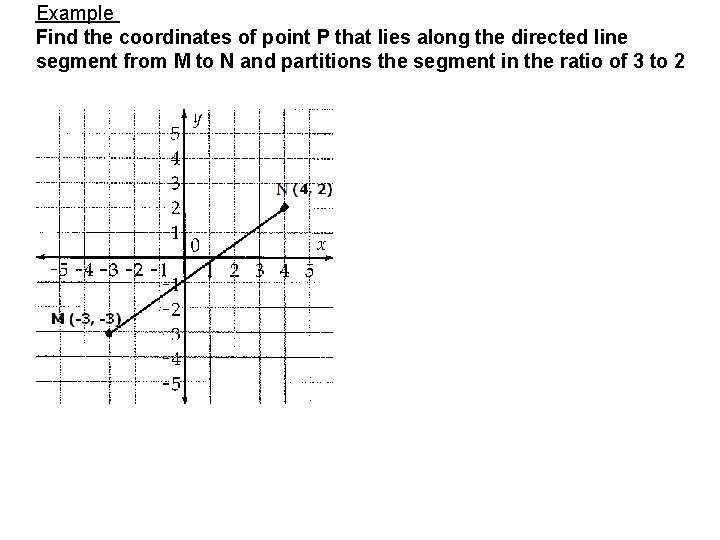
Example Find the coordinates of point P that lies along the directed line segment from M to N and partitions the segment in the ratio of 3 to 2

Essential question: • How do you find the point on a directed line segment that partitions the segment in a given ratio?