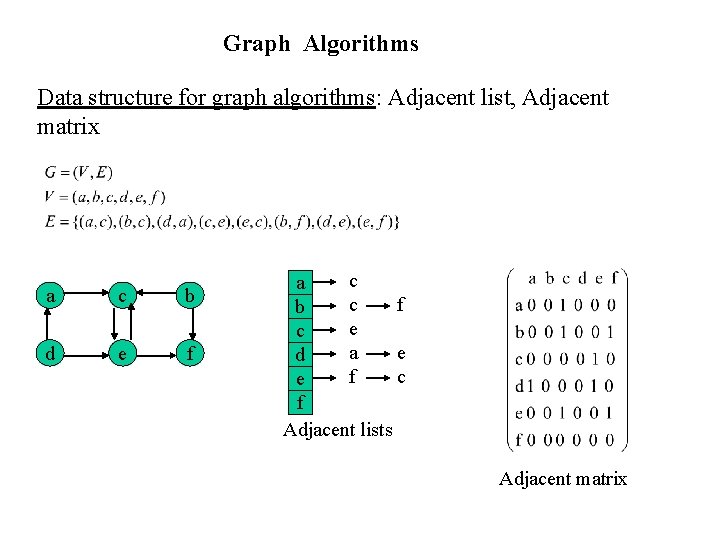
Graph Algorithms Data structure for graph algorithms Adjacent

Graph Algorithms Data structure for graph algorithms: Adjacent list, Adjacent matrix a c b d e f c a c f b e c a e d f c e f Adjacent lists Adjacent matrix

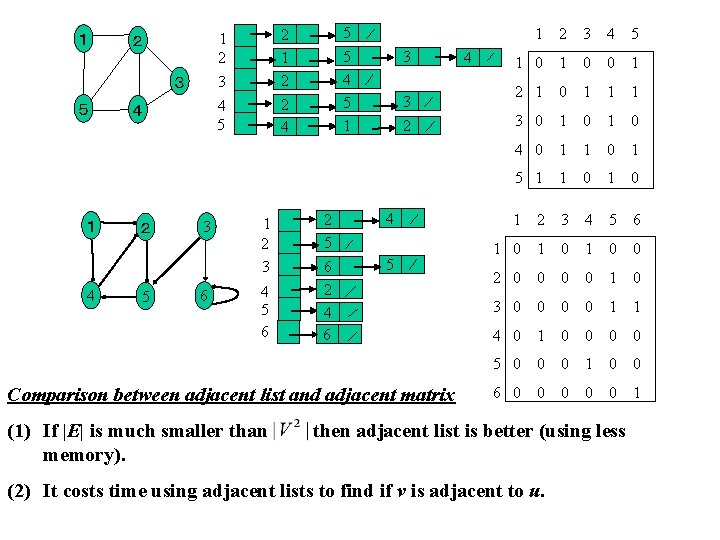
Adjacent list: Each vertex u has an adjacent list Adj[u] (1) For a connected graph G, if G is directed graph the total size of all the adjacent lists is |E|, and if G is undirected graph then the total size of all the adjacent lists is 2|E|. Generally, the total size of adjacent lists is O(V+E). (2) For a weighted graph G, weight w(u, v) of edge (u, v) is kept in Adj[u] with vertex v. Adjacent matrix : Each vertex is given a number from 1, 2, …, |V|. (1) For a undirected graph, its adjacent matrix is symmetric. (2) For a weighted graph, weight w(u, v) is kept in its adjacent matrix at row i and column j.

１ ３ ５ １ 4 4 5 ４ ２ 5 3 6 5 5 4 5 1 2 2 4 1 2 3 ２ 1 2 3 4 5 6 2 4 6 3 3 2 4 5 Comparison between adjacent list and adjacent matrix (1) If |E| is much smaller than memory). 4 1 2 3 4 5 1 0 0 1 2 1 0 1 1 1 3 0 1 0 4 0 1 1 0 1 5 1 1 0 1 2 3 4 5 6 1 0 1 0 0 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 0 0 1 0 0 6 0 0 0 1 then adjacent list is better (using less (2) It costs time using adjacent lists to find if v is adjacent to u.

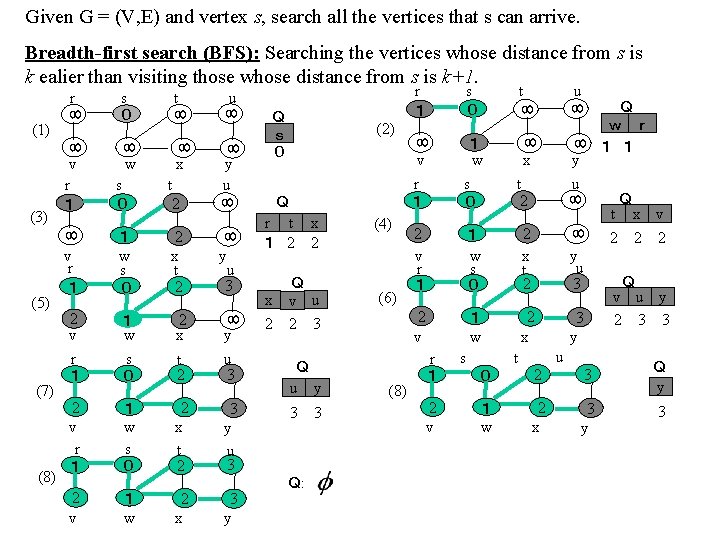
Given G = (V, E) and vertex s, search all the vertices that s can arrive. (7) (8) Ｑ r t x １ 2 2 2 x t 2 2 v １ w 2 x y r １ s ０ t 2 u 3 Ｑ u y 2 v r １ １ w s ０ 2 x t 2 3 y u 3 3 2 v １ w 2 x 3 y ８ v r １ １ w s ０ y u 3 Ｑ x v u 2 2 3 Ｑ: 3 (4) (6) (8) ８ r １ ８ v １ w u ８ t 2 t x y s ０ t 2 u 2 v r １ １ w s ０ 2 x t 2 2 v １ w 2 x 3 y r １ 2 v s t y u 3 u Ｑ ｗ ｒ １ １ Ｑ ８ s ０ (2) s ０ ８ y u Ｑ ｓ ０ r １ ８ ８ x ８ ８ w ８ (5) u v r １ ８ (3) t ８ (1) s ０ ８ ８ r ８ Breadth-first search (BFS): Searching the vertices whose distance from s is k ealier than visiting those whose distance from s is k+1. t x v 2 2 2 Ｑ v u y 2 3 3 ０ 2 3 Ｑ y １ w 2 x 3 y 3

Analysis of the algorithm (1) Each vertex is put into queue Q at most once. Therefore, the number of operation for the queue is O(|V|). (2) Each adjacent list is at most scanned once. Therefore, the total running time for scanning adjacent lists is O(|E|). (3) The running time for initiation is O(|V|). (4) Therefore, the total running time of the algorithm is O(|V|+|E|).

Find the path from s to v in BSF

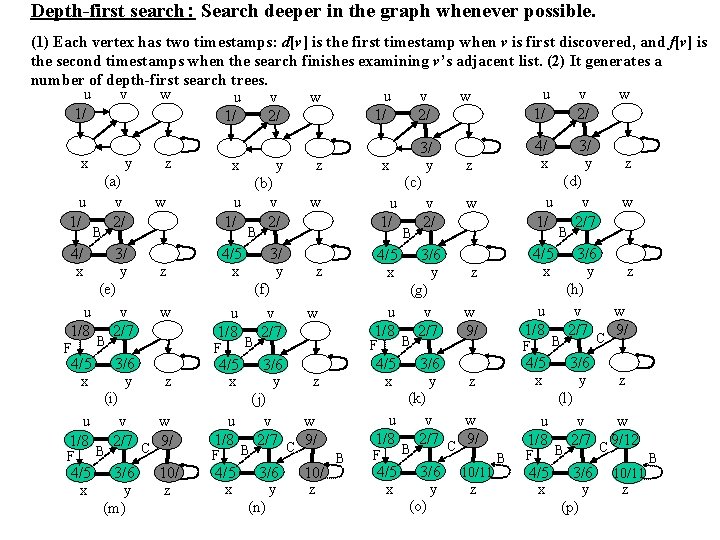
Depth-first search： Search deeper in the graph whenever possible. (1) Each vertex has two timestamps: d[v] is the first timestamp when v is first discovered, and f[v] is the second timestamps when the search finishes examining v’s adjacent list. (2) It generates a number of depth-first search trees. u v w 1/ 1/ 2/ x u 1/ y B (a) v 2/ 4/ x 3/ y (e) u v 1/8 2/7 F z w B 3/6 y z (i) u v w 1/8 2/7 C 9/ B 4/5 x 3/6 y (m) y z (b) u v 1/ 2/ w B 4/5 x F x 3/ x y (c) u v 1/ 2/ 10/ z 4/5 x 3/ y (f) u v 1/8 2/7 F B 4/5 x 3/6 y (g) u v 1/8 2/7 z w F 3/6 y z (j) u v w 1/8 2/7 C 9/ 3/6 y (n) 3/ y (d) u v 1/ 2/7 z w 10/ z B 4/5 x z u 1/8 w 9/ 3/6 y z (k) u v w 1/8 2/7 C 9/ B F F 4/5 x 3/6 y (o) w 10/11 z B 3/6 y z (h) v w 2/7 C 9/ 4/5 x B z B B 4/5 x 4/ x B 3/6 y z (l) u v w 1/8 2/7 C 9/12 B F 4/5 x 3/6 y (p) 10/11 z B

Running time (1) The running time except DFS-VIST is O(|V|). 1. (2) Each vertex is called by DFS-VISIT only once, because only white vertices will be called by DES-VISIT and when they are called their color is changed to gray immediately. 2. (3) The loop in DFS-VISIT is executed only |Adj[v]| times. Therefore, the total running time of the algorithm is O(|V|+|E|).