CS 6045 Advanced Algorithms Graph Algorithms Graph Representation

CS 6045: Advanced Algorithms Graph Algorithms

Graph Representation • A graph G = (V, E) – V = set of vertices – E = set of edges = subset of V V – Thus |E| = O(|V|2)

Graph Variations • Variations: – A connected graph has a path from every vertex to every other – In an undirected graph: • Edge (u, v) = edge (v, u) • No self-loops – In a directed graph: • Edge (u, v) goes from vertex u to vertex v, notated u v

Graph Variations • More variations: – A weighted graph associates weights with either the edges or the vertices • e. g. , a road map: edges might be weighted with distance – A hypergraph allows multiple edges between the same vertices • e. g. , the call graph in a program (a function can get called from multiple points in another function)

Graphs • We will typically express running times in terms of |E| and |V| – If |E| |V|2 the graph is dense – If |E| |V| the graph is sparse • If you know you are dealing with dense or sparse graphs, different data structures may make sense

Representing Graphs • Assume V = {1, 2, …, n} • An adjacency matrix represents the graph as a n x n matrix A: if edge (i, j) E – A[i, j] = 1, = 0, – A[i, j] = weight on the edge, if edge (i, j) E = 0, if edge (i, j) E

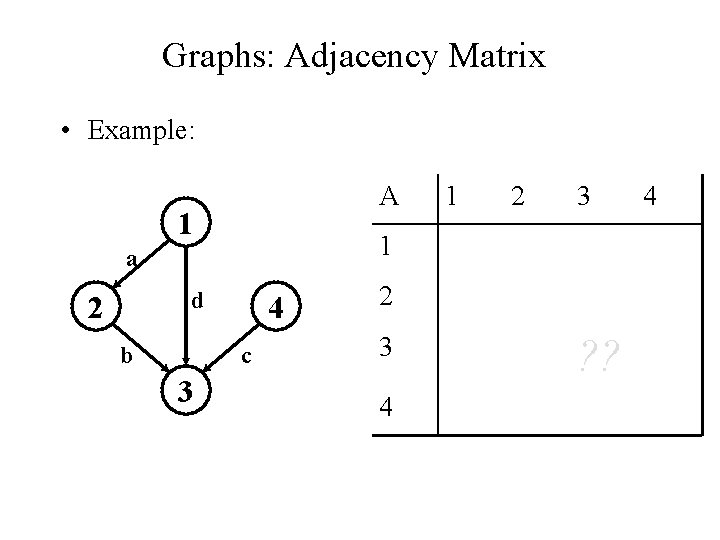
Graphs: Adjacency Matrix • Example: A 1 d b 4 c 3 2 3 1 a 2 1 2 3 4 ? ? 4

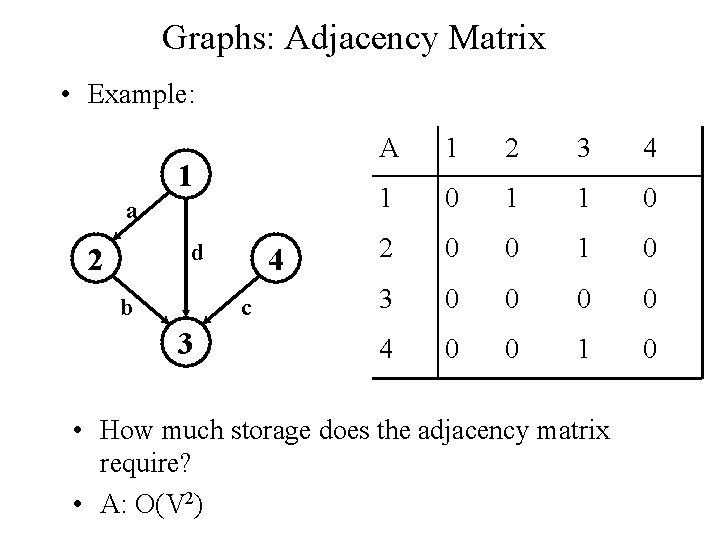
Graphs: Adjacency Matrix • Example: 1 a d 2 b 4 c 3 A 1 2 3 4 1 0 1 1 0 2 0 0 1 0 3 0 0 4 0 0 1 0 • How much storage does the adjacency matrix require? • A: O(V 2)

Graphs: Adjacency Matrix • The adjacency matrix is a dense representation – Usually too much storage for large graphs – But can be very efficient for small graphs • Most large interesting graphs are sparse – e. g. , planar graphs, in which no edges cross, have |E| = O(|V|) by Euler’s formula – For this reason the adjacency list is often a more appropriate representation

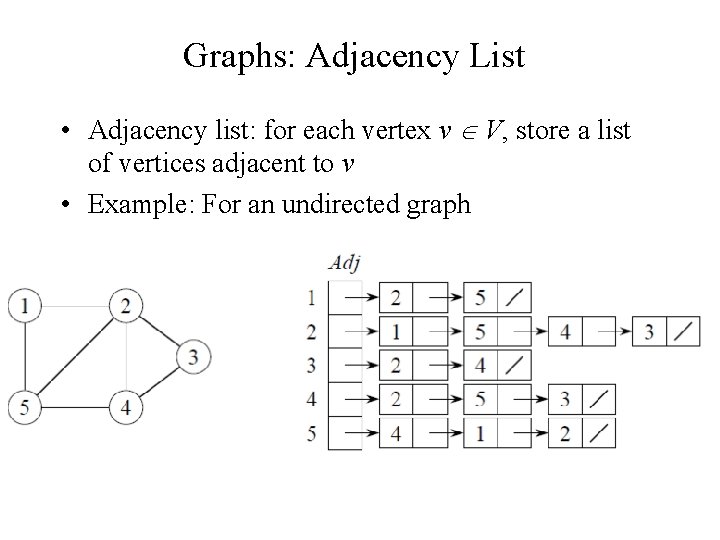
Graphs: Adjacency List • Adjacency list: for each vertex v V, store a list of vertices adjacent to v • Example: For an undirected graph

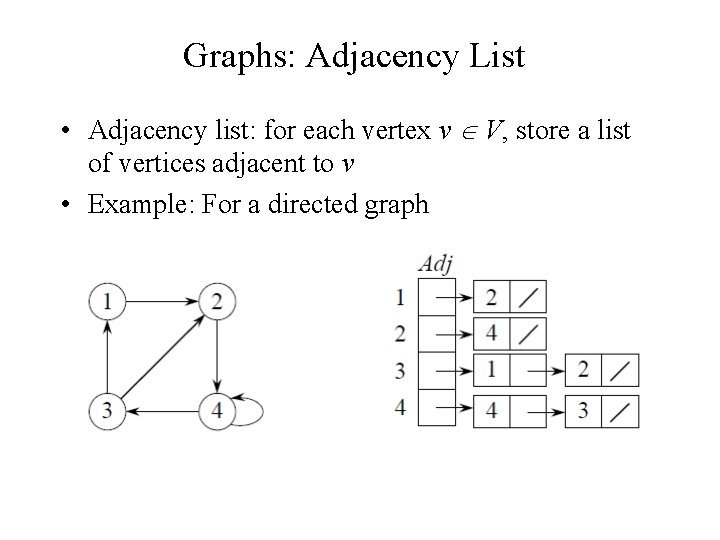
Graphs: Adjacency List • Adjacency list: for each vertex v V, store a list of vertices adjacent to v • Example: For a directed graph

Graphs: Adjacency List • How much storage is required? – The degree of a vertex v = # of edges • Directed graphs have in-degree, out-degree – For directed graphs, # of items in adjacency lists is out-degree(v) = |E| takes O(V + E) storage – For undirected graphs, # items in adjacency lists is degree(v) = 2 |E| (handshaking lemma) also O(V + E) storage • So: Adjacency lists take O(V+E) storage

Graph Searching • Given: a graph G = (V, E), directed or undirected • Goal: methodically explore every vertex and every edge • Ultimately: build a tree on the graph – Pick a vertex as the root – Choose certain edges to produce a tree – Note: might also build a forest if graph is not connected

Breadth-First Search • “Explore” a graph, turning it into a tree – One vertex at a time – Expand frontier of explored vertices across the breadth of the frontier • Builds a tree over the graph – Pick a source vertex to be the root – Find (“discover”) its children, then their children, etc.

Breadth-First Search • Again will associate vertex “colors” to guide the algorithm – White vertices have not been discovered • All vertices start out white – Grey vertices are discovered but not fully explored • They may be adjacent to white vertices – Black vertices are discovered and fully explored • They are adjacent only to black and gray vertices • Explore vertices by scanning adjacency list of grey vertices

Breadth-First Search BFS(G, s) { initialize vertices V. d = ; s. d = 0; Q = {s}; // Q is a queue; initialize to s while (Q not empty) { u = Dequeue(Q); for each v u->adj { if (v->color == WHITE) v->color = GREY; v->d = u->d + 1; What does v->d represent? v->p = u; What does v->p represent? Enqueue(Q, v); } u->color = BLACK; } }

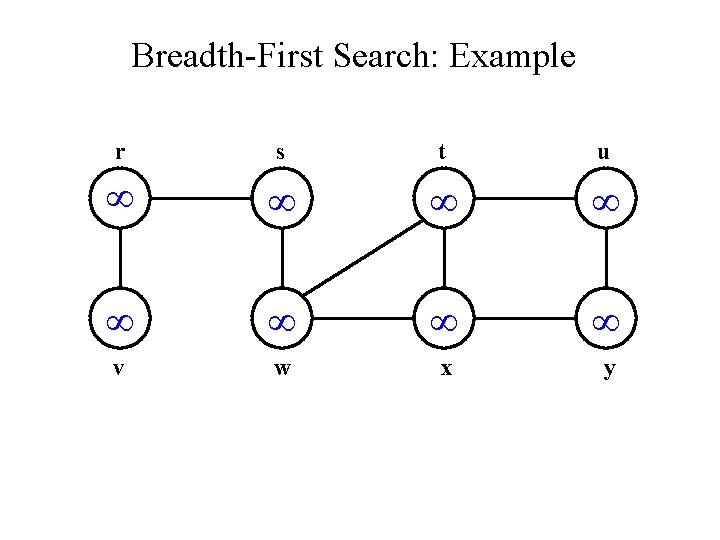
Breadth-First Search: Example r s t u v w x y

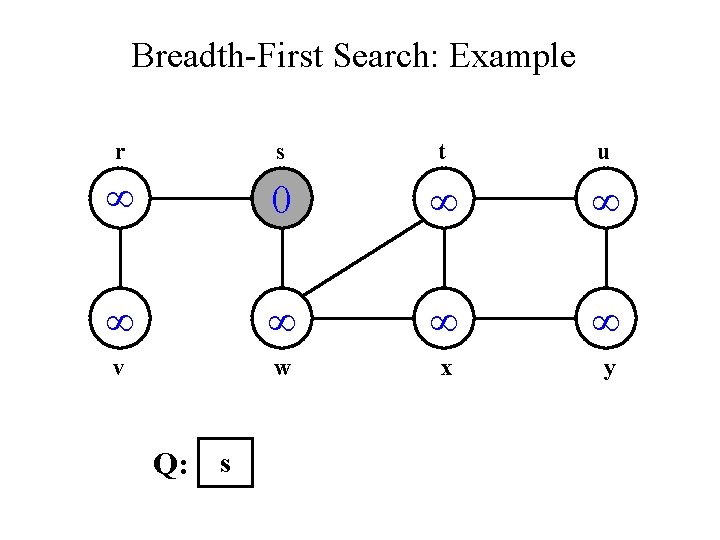
Breadth-First Search: Example r s t u 0 v w x y Q: s

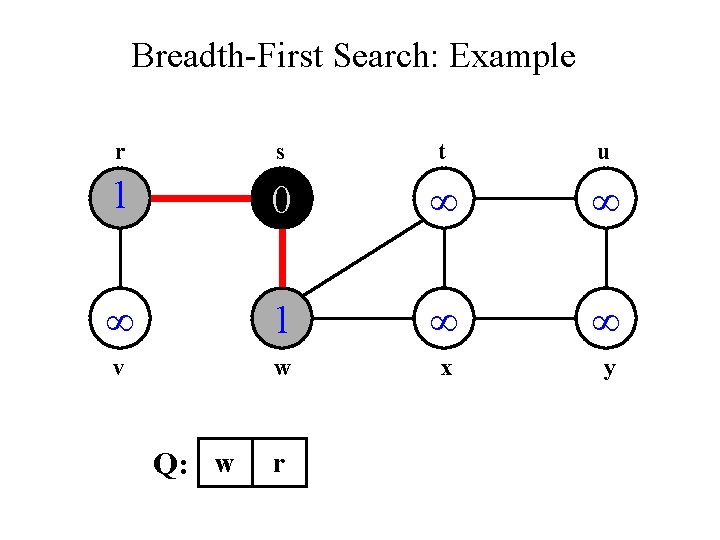
Breadth-First Search: Example r s t u 1 0 1 v w x y Q: w r

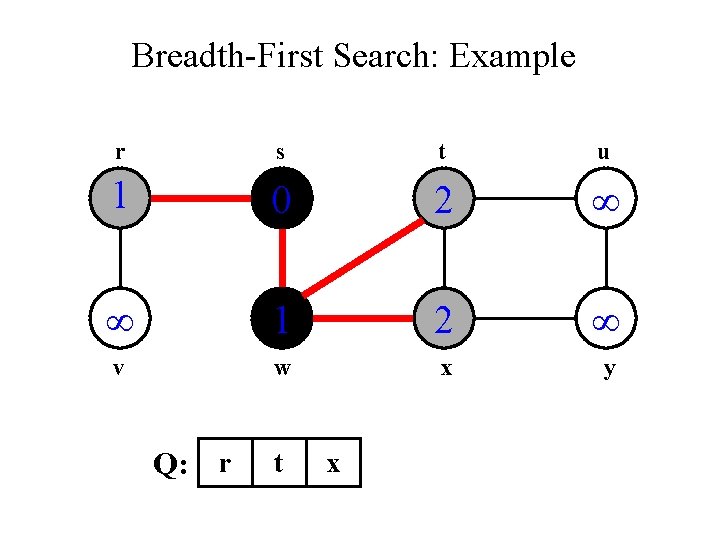
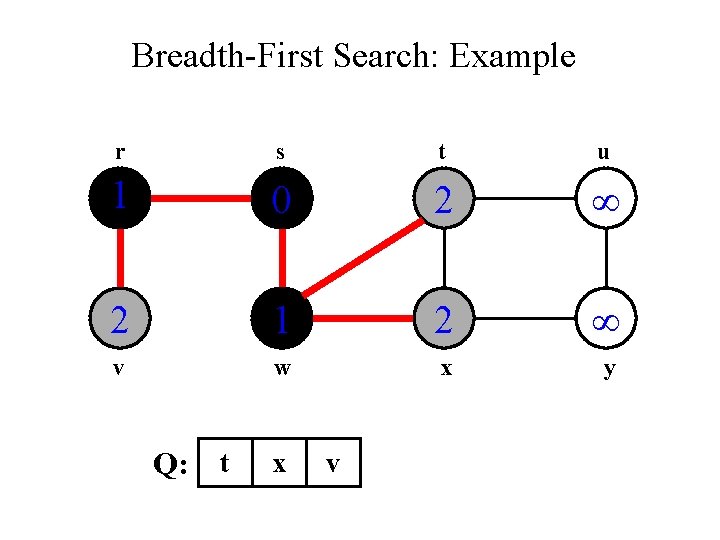
Breadth-First Search: Example r s t u 1 0 2 1 2 v w x y Q: r t x

Breadth-First Search: Example r s t u 1 0 2 2 1 2 v w x y Q: t x v

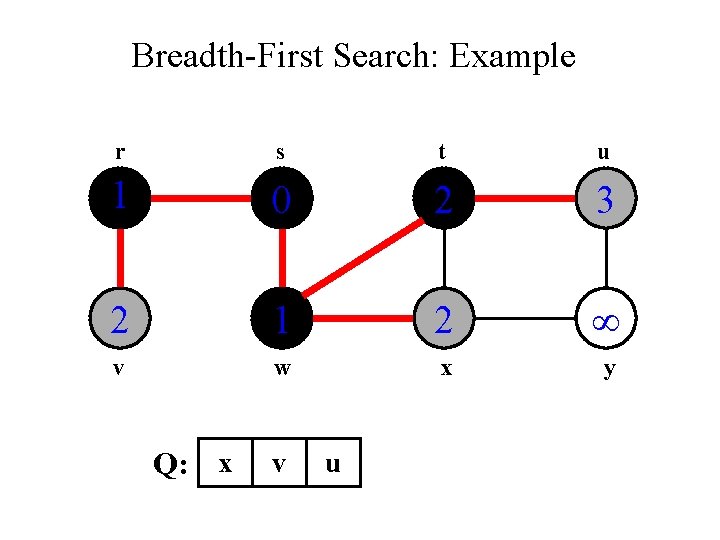
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 v w x y Q: x v u

Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: v u y

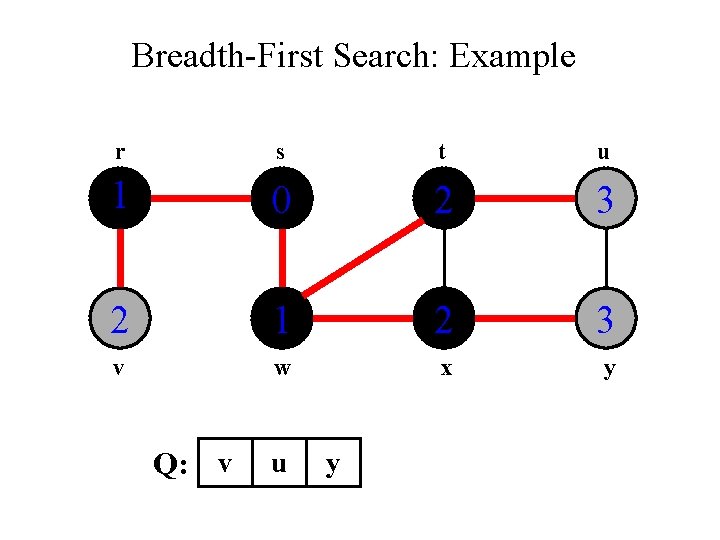
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: u y

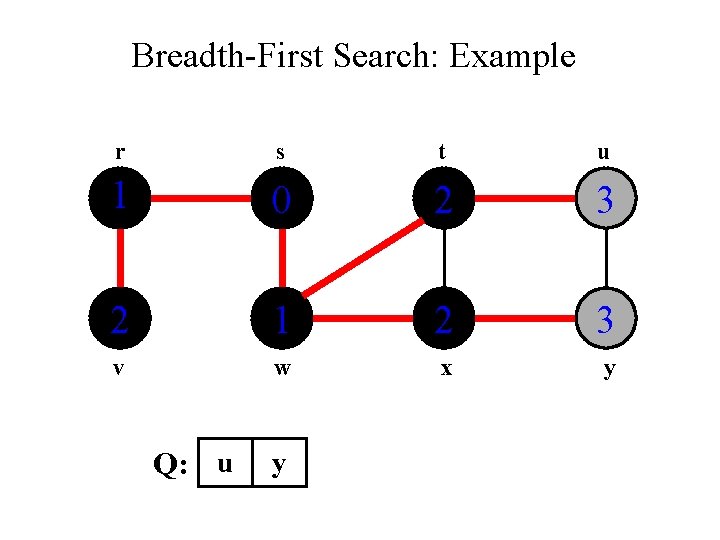
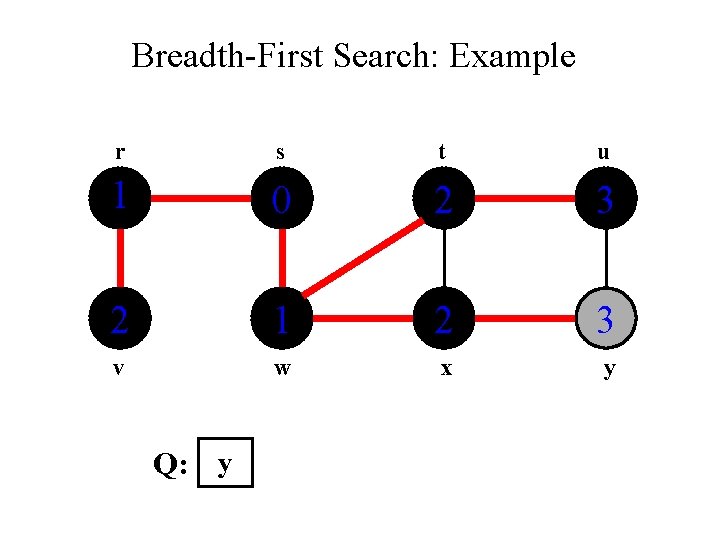
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: y

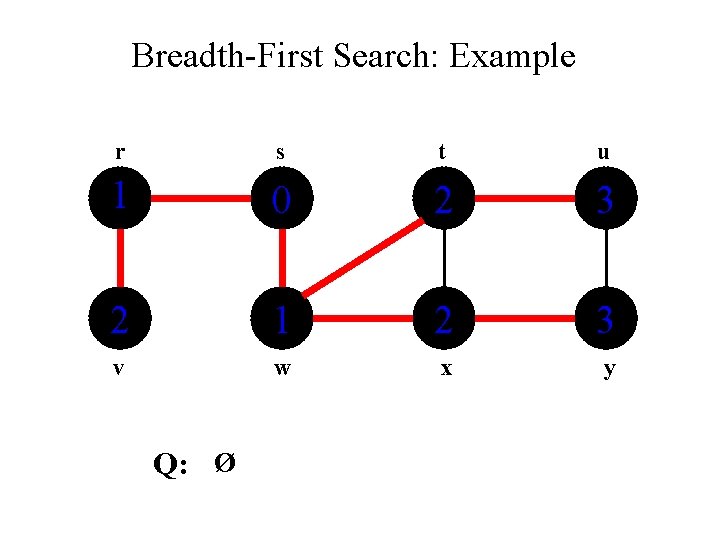
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: Ø

BFS: The Code Again BFS(G, s) { Touch every vertex: O(V) initialize vertices V. d = ; s. d = 0; Q = {s}; while (Q not empty) { u = Dequeue(Q); u = every vertex, but only once for each v u->adj { if (v->color == WHITE) v = every vertex v->color = GREY; v->d = u->d + 1; that appears in some other vert’s v->p = u; Enqueue(Q, v); adjacency list } What will be the running time? u->color = BLACK; Total running time: O(V+E) } }

BFS: The Code Again BFS(G, s) { initialize vertices V. d = ; s. d = 0; Q = {s}; while (Q not empty) { u = Dequeue(Q); for each v u->adj { if (v->color == WHITE) v->color = GREY; v->d = u->d + 1; v->p = u; Enqueue(Q, v); What will be the storage cost } in addition to storing the tree? u->color = BLACK; Total space used: } O(max(degree(v))) = O(E) }

Breadth-First Search: Properties • BFS calculates the shortest-path distance to the source node – Shortest-path distance (s, v) = minimum number of edges from s to v, or if v not reachable from s • BFS builds breadth-first tree, in which paths to root represent shortest paths in G – Thus can use BFS to calculate shortest path from one vertex to another in O(V+E) time

Depth-First Search • Depth-first search is another strategy for exploring a graph – Explore “deeper” in the graph whenever possible – Edges are explored out of the most recently discovered vertex v that still has unexplored edges – When all of v’s edges have been explored, backtrack to the vertex from which v was discovered

Depth-First Search • Vertices initially colored white • Then colored gray when discovered • Then black when finished

Depth-First Search: The Code DFS(G) { for each vertex u G>V { u->color = WHITE; } time = 0; for each vertex u G>V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; What does u->d represent? for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; What does u->f represent? } Will all vertices eventually be colored black? What will be the running time?

Depth-First Search: The Code DFS(G) { for each vertex u G>V { u->color = WHITE; } time = 0; for each vertex u G>V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } Running time: O(n 2) because call DFS_Visit on each vertex, and the loop over Adj[] can run as many as |V| times

Depth-First Search: The Code DFS(G) { for each vertex u G>V { u->color = WHITE; } time = 0; for each vertex u G>V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } BUT, there is actually a tighter bound. Running time of DFS = O(V+E)

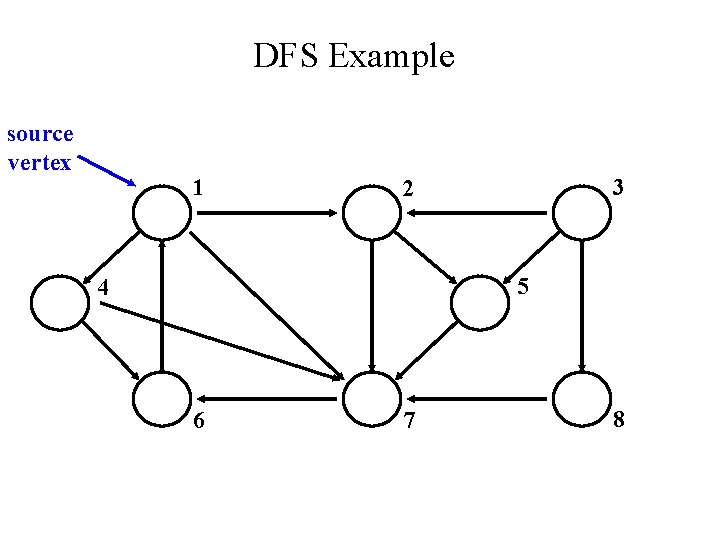
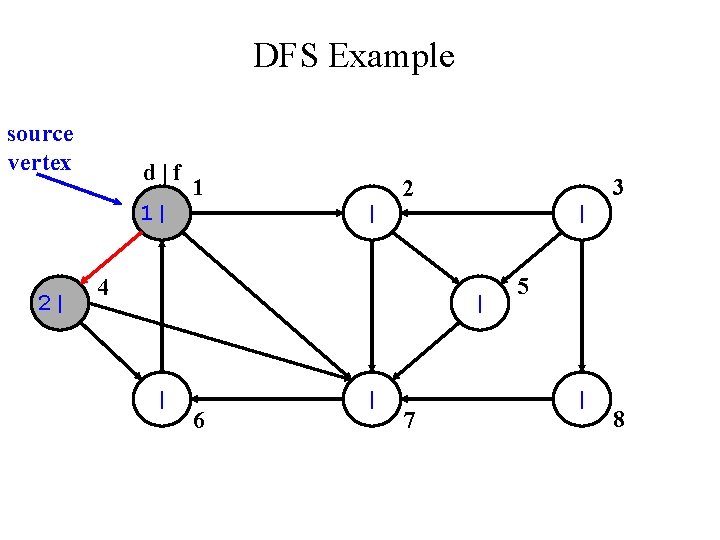
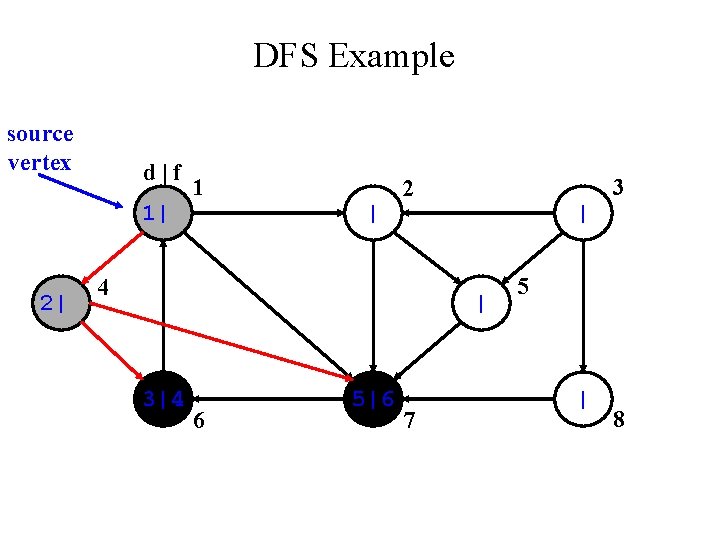
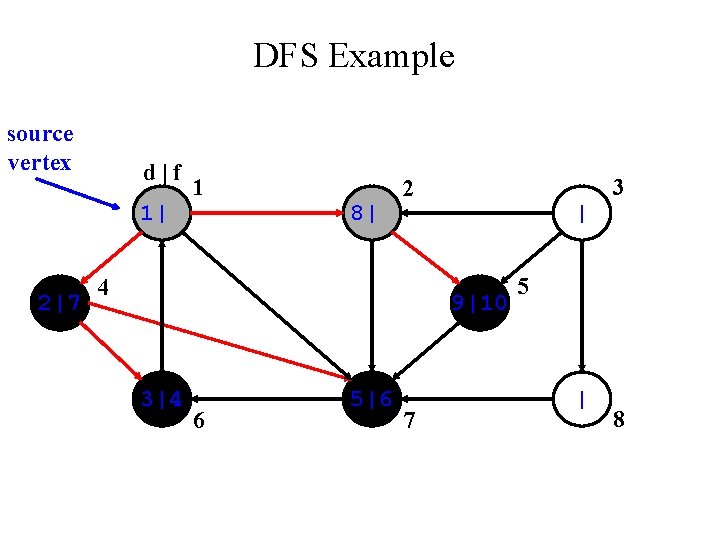
DFS Example source vertex 1 3 2 5 4 6 7 8

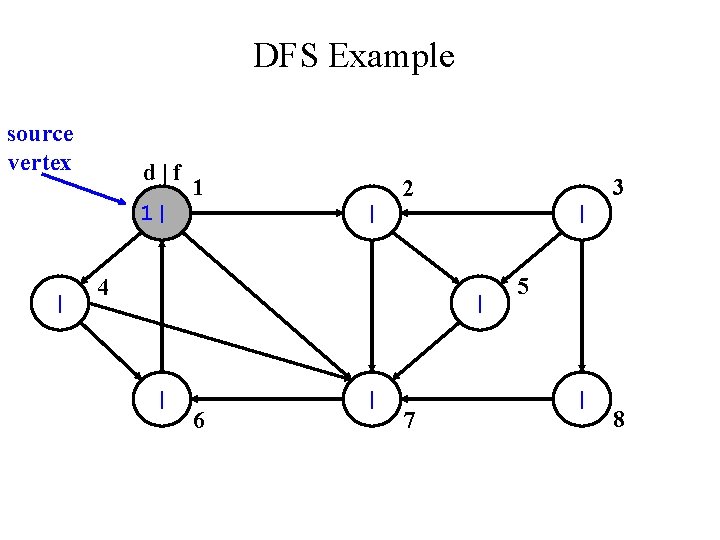
DFS Example source vertex d|f 1| | 1 | 3 2 4 | | | 6 | 7 5 | 8

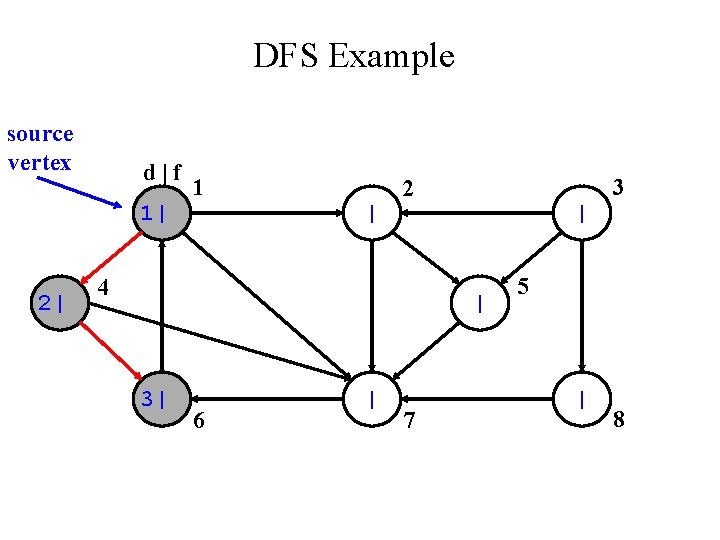
DFS Example source vertex d|f 1| 2| 1 | 3 2 4 | | | 6 | 7 5 | 8

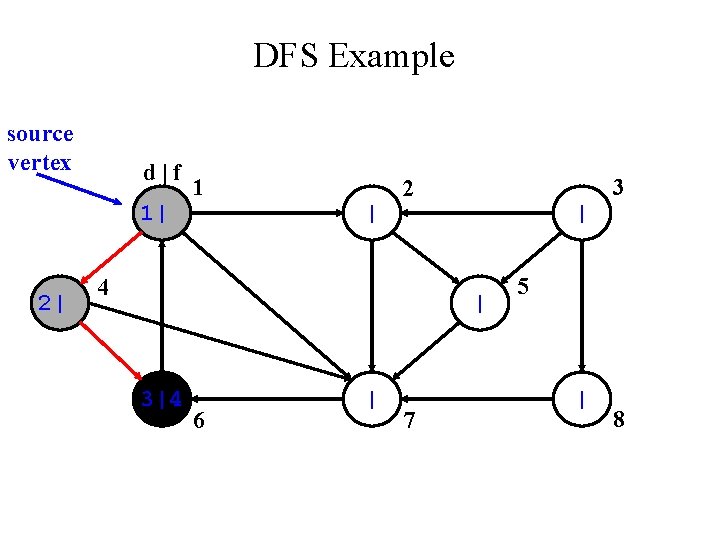
DFS Example source vertex d|f 1| 2| 1 | 3 2 4 | | 3| 6 | 7 5 | 8

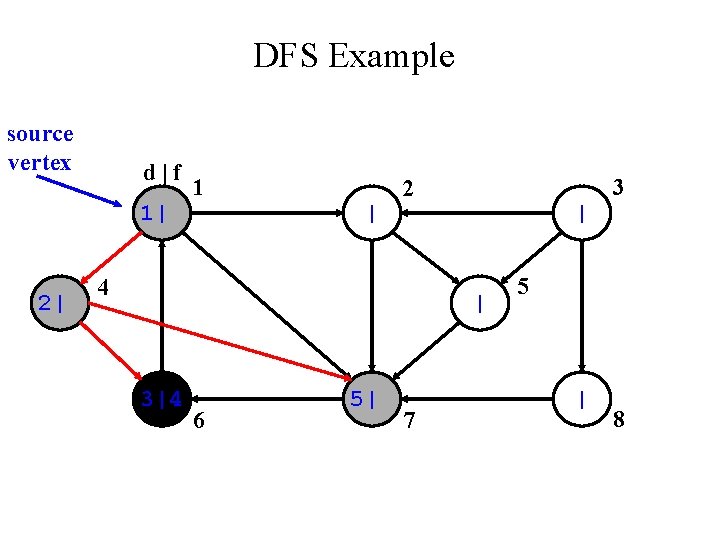
DFS Example source vertex d|f 1| 2| 1 | 3 2 4 | | 3|4 6 | 7 5 | 8

DFS Example source vertex d|f 1| 2| 1 | 3 2 4 | | 3|4 6 5| 7 5 | 8

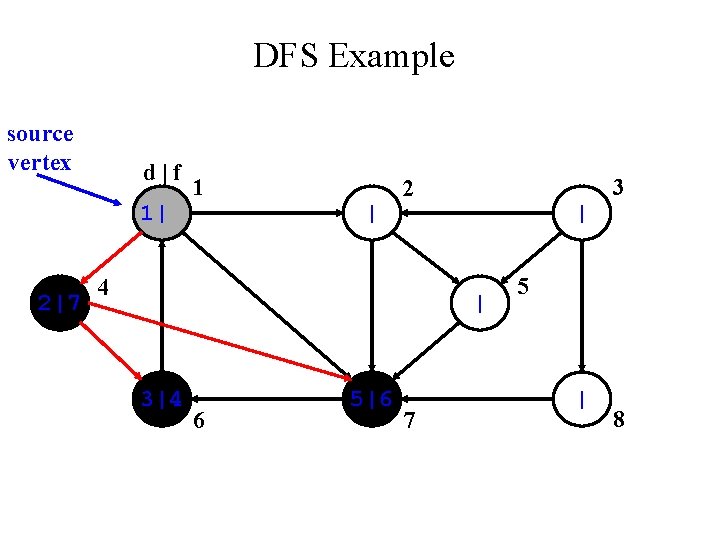
DFS Example source vertex d|f 1| 2| 1 | 3 2 4 | | 3|4 6 5|6 7 5 | 8

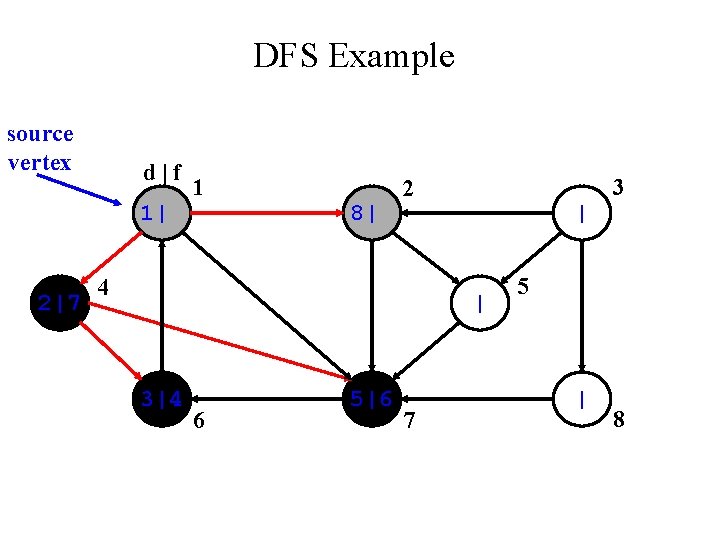
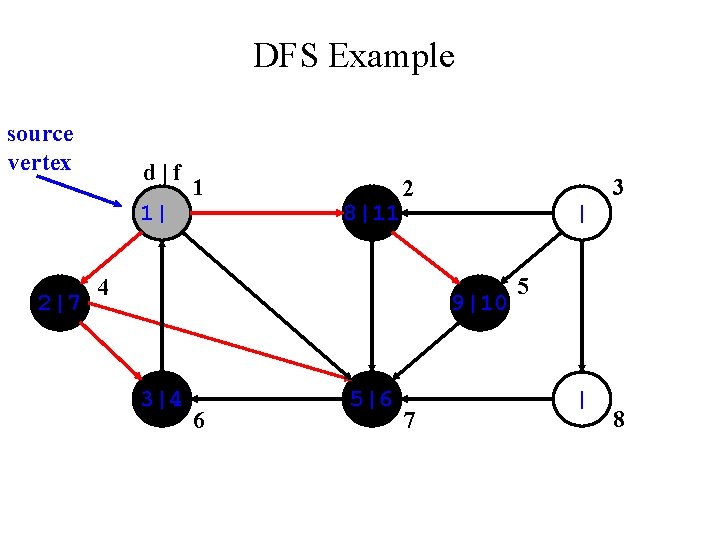
DFS Example source vertex d|f 1| 2|7 1 | 3 2 4 | | 3|4 6 5|6 7 5 | 8

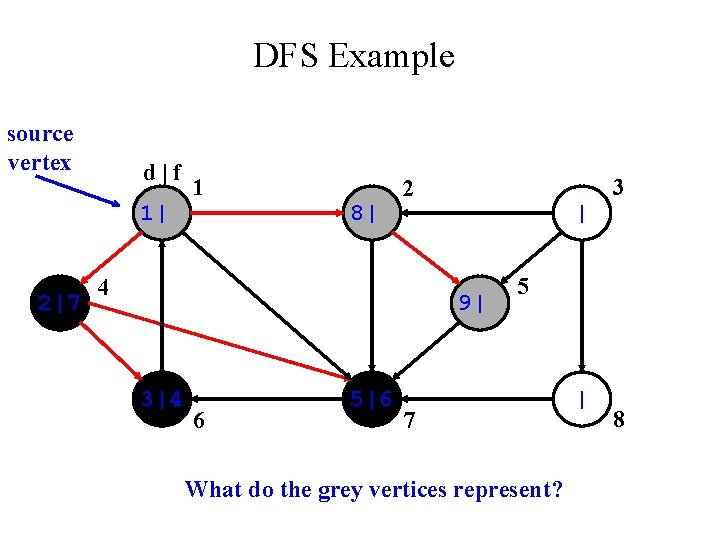
DFS Example source vertex d|f 1| 2|7 1 8| 3 2 4 | | 3|4 6 5|6 7 5 | 8

DFS Example source vertex d|f 1| 2|7 1 8| 3 2 4 | 9| 3|4 6 5|6 5 7 What do the grey vertices represent? | 8

DFS Example source vertex d|f 1| 2|7 1 8| 3 2 4 | 9|10 3|4 6 5|6 7 5 | 8

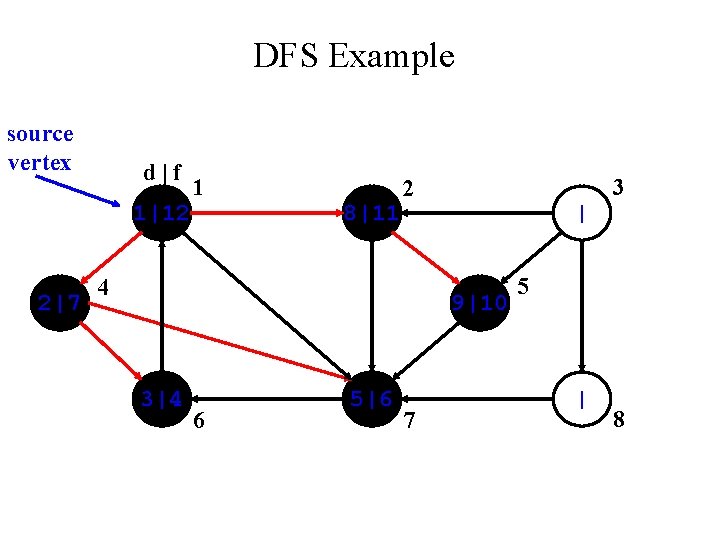
DFS Example source vertex d|f 1| 2|7 1 8|11 3 2 4 | 9|10 3|4 6 5|6 7 5 | 8

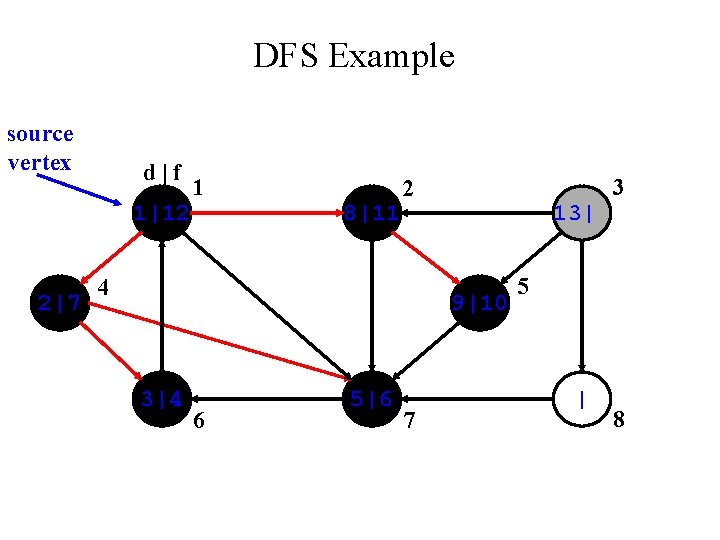
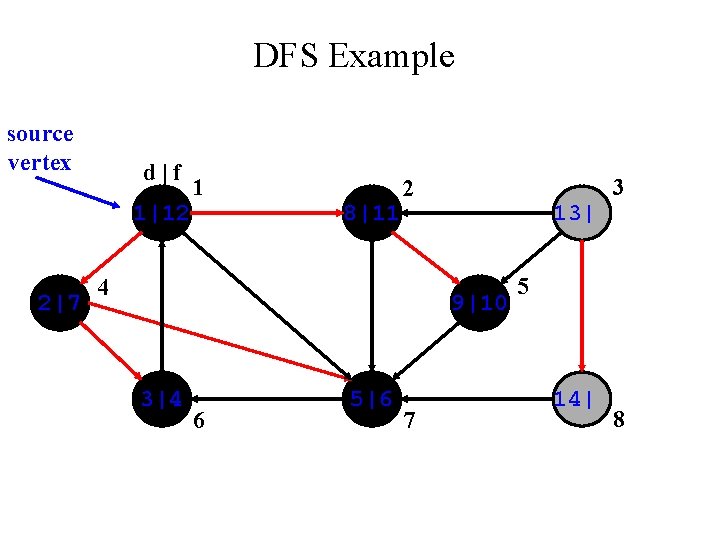
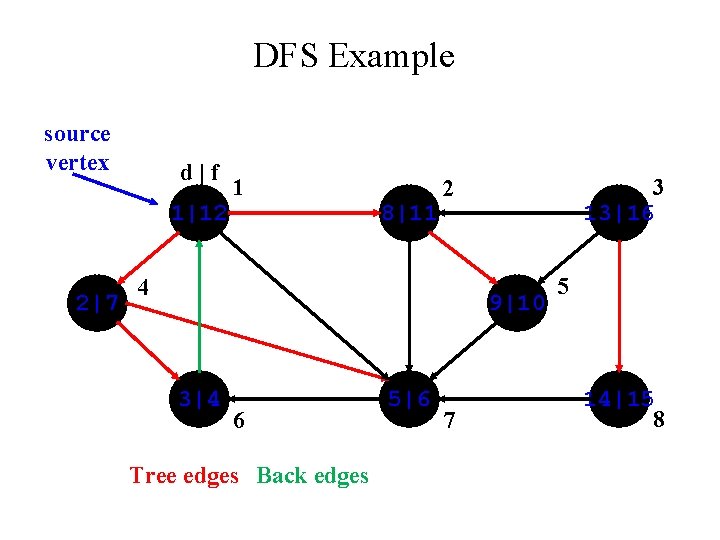
DFS Example source vertex d|f 1|12 2|7 1 8|11 3 2 4 | 9|10 3|4 6 5|6 7 5 | 8

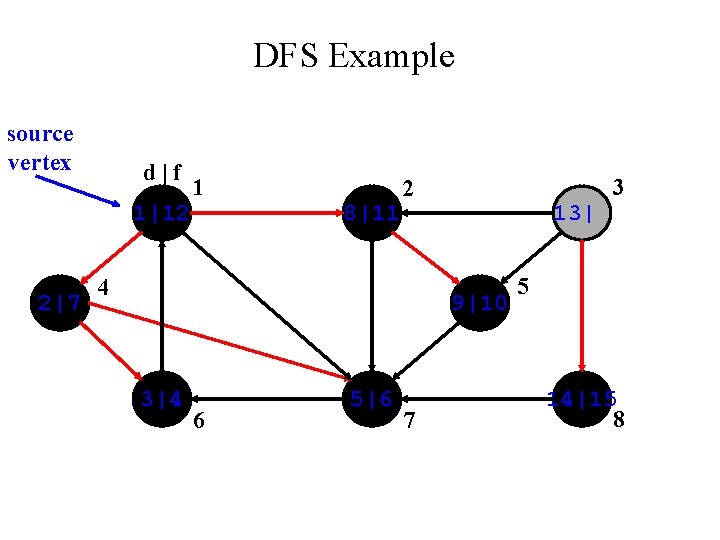
DFS Example source vertex d|f 1|12 2|7 1 8|11 3 2 4 13| 9|10 3|4 6 5|6 7 5 | 8

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 2 4 13| 9|10 3|4 6 5|6 7 5 14| 8

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 2 4 13| 9|10 3|4 6 5|6 7 5 14|15 8

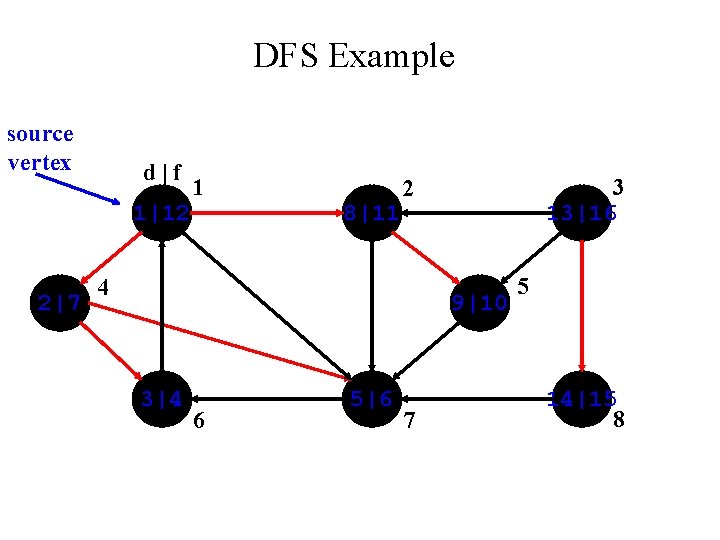
DFS Example source vertex d|f 1|12 2|7 1 8|11 3 13|16 2 4 9|10 3|4 6 5|6 7 5 14|15 8

DFS Properties • Parenthesis Theorem – For all u, v, exactly one of the following holds: 1. The intervals [u. d, u. f] and [v. d, v. f] are disjoint, neither of u and v is a descendant of the other 2. The interval [u. d, u. f] is contained entirely within the interval [v. d, v. f], u is a descendant of v in a depth-first tree 3. The interval [u. d, u. f] is contained entirely within the interval [v. d, v. f], v is a ancestor of u in a depth-first tree • Corollary – v is a proper descendant of u if and only if u. d<v. f<u. f

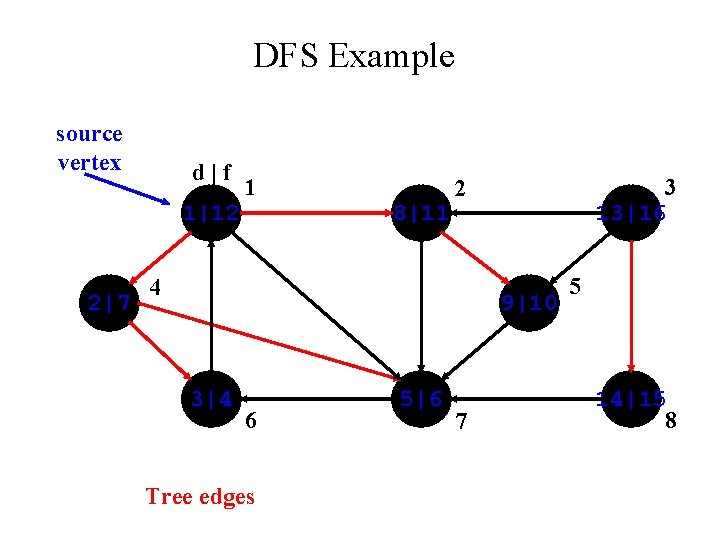
DFS: Kinds of edges • DFS introduces an important distinction among edges in the original graph: – Tree edge: encounter new (white) vertex • The tree edges form a spanning forest • Can tree edges form cycles? Why or why not?

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 13|16 2 4 9|10 3|4 6 Tree edges 5|6 7 5 14|15 8

DFS: Kinds of edges • DFS introduces an important distinction among edges in the original graph: – Tree edge: encounter new (white) vertex – Back edge: from descendent to ancestor • Encounter a grey vertex (grey to grey)

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 13|16 2 4 9|10 3|4 6 Tree edges Back edges 5|6 7 5 14|15 8

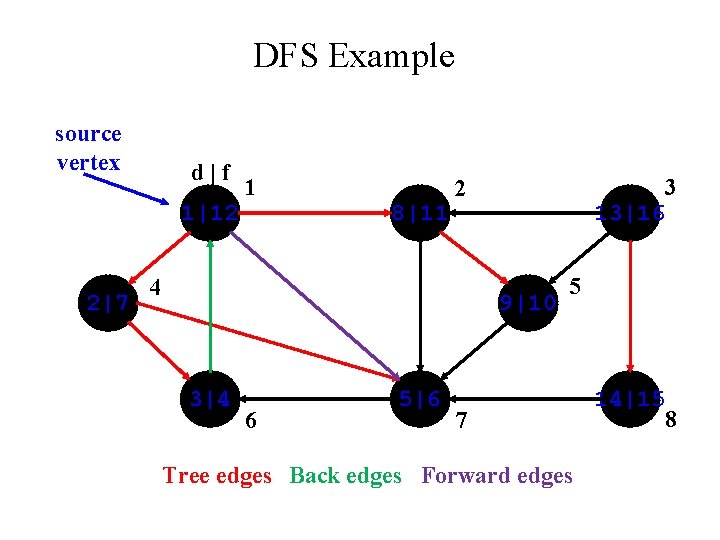
DFS: Kinds of edges • DFS introduces an important distinction among edges in the original graph: – Tree edge: encounter new (white) vertex – Back edge: from descendent to ancestor – Forward edge: from ancestor to descendent • Not a tree edge • From grey node to black node

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 13|16 2 4 9|10 3|4 6 5|6 5 7 Tree edges Back edges Forward edges 14|15 8

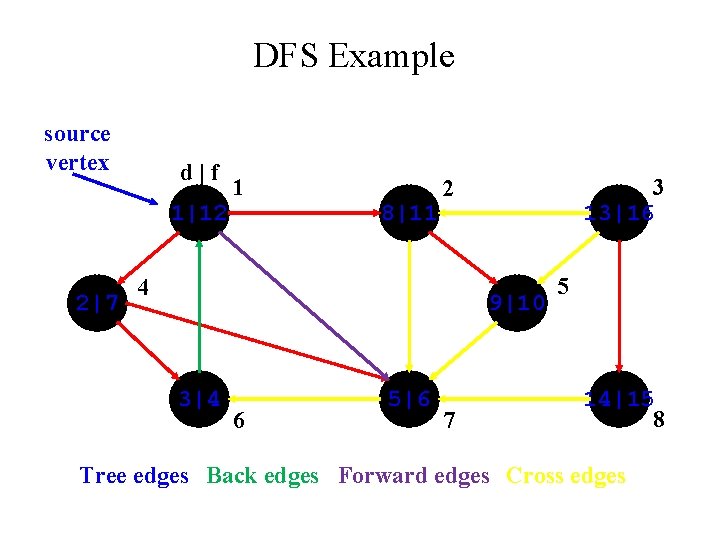
DFS: Kinds of edges • DFS introduces an important distinction among edges in the original graph: – – Tree edge: encounter new (white) vertex Back edge: from descendent to ancestor Forward edge: from ancestor to descendent Cross edge: between a tree or subtrees • Any other edges • From a grey node to a black node

DFS Example source vertex d|f 1|12 2|7 1 8|11 3 13|16 2 4 9|10 3|4 6 5|6 7 5 14|15 8 Tree edges Back edges Forward edges Cross edges

DFS: Kinds of edges • DFS introduces an important distinction among edges in the original graph: – – Tree edge: encounter new (white) vertex Back edge: from descendent to ancestor Forward edge: from ancestor to descendent Cross edge: between a tree or subtrees • Note: If G is undirected, a DFS produces only tree and back edges. No forward or cross edges.

DFS And Graph Cycles • Theorem: An undirected graph is acyclic iff a DFS yields no back edges – If acyclic, no back edges (because a back edge implies a cycle – If no back edges, acyclic • No back edges implies only tree edges • Only tree edges implies we have a tree or a forest • Which by definition is acyclic • Thus, can run DFS to find whether a graph has a cycle

Directed Acyclic Graphs • A directed acyclic graph or DAG is a directed graph with no directed cycles:

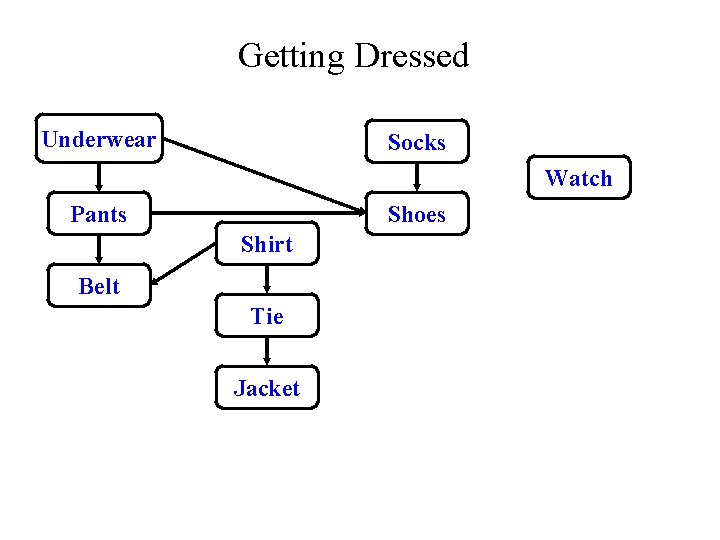
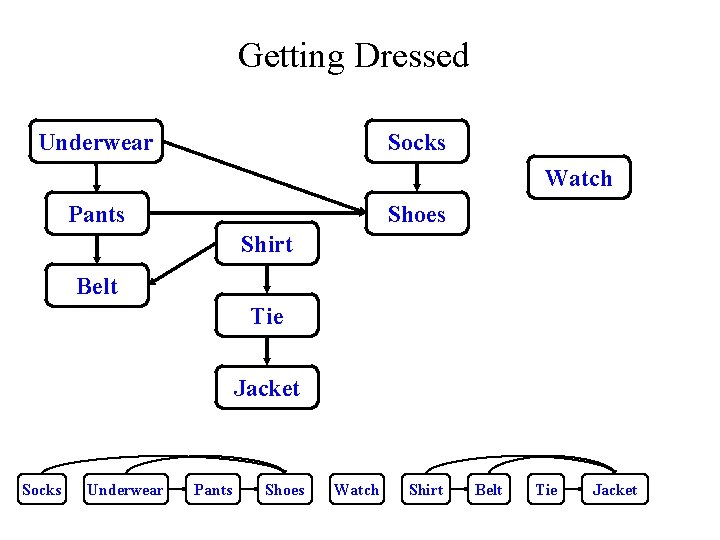
Topological Sort • Topological sort of a DAG: – Linear ordering of all vertices in graph G such that vertex u appears somewhere before vertex v if edge (u, v) G • Real-world example: getting dressed

Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket

Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket Socks Underwear Pants Shoes Watch Shirt Belt Tie Jacket

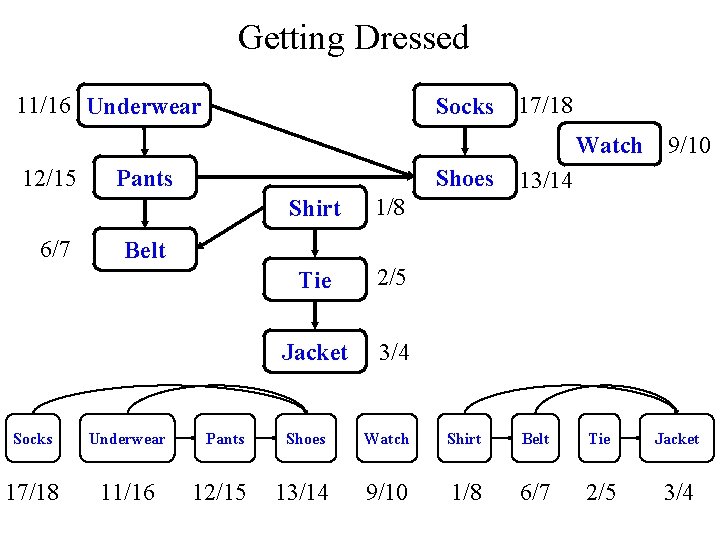
Topological Sort Algorithm Topological-Sort() { Run DFS to compute finish time v. f for all v V Output vertices in order of decreasing finishing times } • Time: O(V+E)

Getting Dressed 11/16 Underwear Socks 17/18 Watch 12/15 6/7 Pants Shoes Shirt 1/8 Tie 2/5 Jacket 3/4 9/10 13/14 Belt Socks Underwear 17/18 11/16 Pants Shoes Watch Shirt Belt Tie Jacket 12/15 13/14 9/10 1/8 6/7 2/5 3/4

Minimum Spanning Tree •

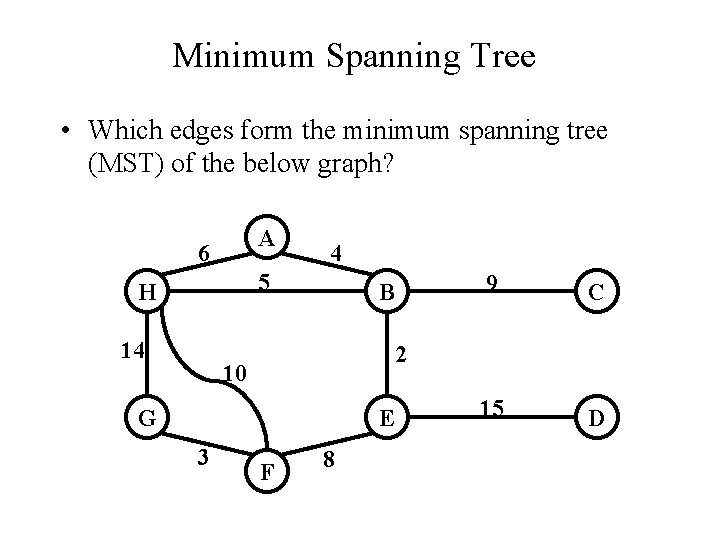
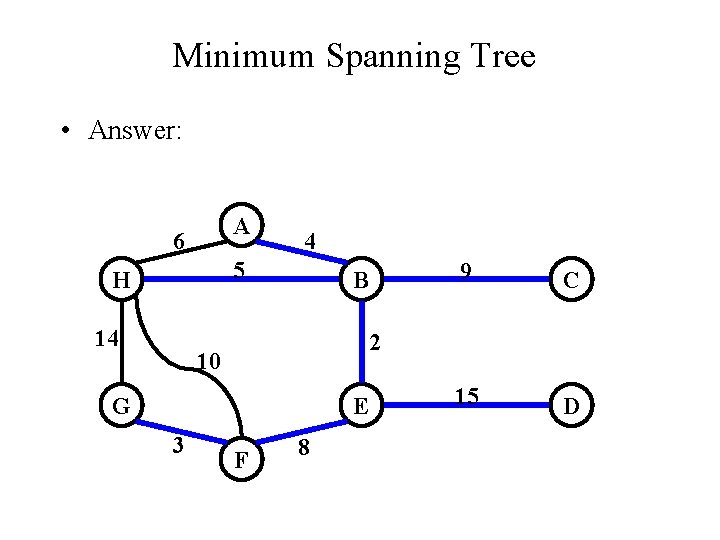
Minimum Spanning Tree • Which edges form the minimum spanning tree (MST) of the below graph? A 6 4 5 H 14 B C 15 D 2 10 G E 3 9 F 8

Minimum Spanning Tree • Answer: A 6 4 5 H 14 B C 15 D 2 10 G E 3 9 F 8

Minimum Spanning Tree • MSTs satisfy the optimal substructure property: an optimal tree is composed of optimal subtrees – Let T be an MST of G with an edge (u, v) in the middle – Removing (u, v) partitions T into two trees T 1 and T 2 – Claim: T 1 is an MST of G 1 = (V 1, E 1), and T 2 is an MST of G 2 = (V 2, E 2) – Proof: w(T) = w(u, v) + w(T 1) + w(T 2)

Minimum Spanning Tree • MSTs satisfy the greedy-choice property: – Let T be MST of G, and let A T be subtree of T – Let (u, v) be min-weight edge connecting A to the rest of the Graph (V - A) – Then (u, v) T

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 for each u Q key[u] = ; 14 2 10 key[r] = 0; p[r] = NULL; 3 while (Q not empty) 8 u = Extract. Min(Q); Run on example for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15 graph

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 for each u Q key[u] = ; 14 2 10 key[r] = 0; p[r] = NULL; 3 while (Q not empty) 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 9 5 for each u Q key[u] = ; 14 2 10 key[r] = 0; 15 0 r p[r] = NULL; 3 while (Q not empty) 8 u = Extract. Min(Q); Pick a start vertex r for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 9 5 for each u Q key[u] = ; 14 2 10 key[r] = 0; 15 0 u p[r] = NULL; 3 while (Q not empty) 8 u = Extract. Min(Q); Red vertices have been removed from Q for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 9 5 for each u Q key[u] = ; 14 2 10 key[r] = 0; 15 0 u p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); Red arrows indicate parent pointers for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 u p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 p[r] = NULL; 3 while (Q not empty) 8 3 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 8 3 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 8 3 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 10 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 5 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm u MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 5 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 5 2 u for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 5 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm MST-Prim(G, w, r) 4 6 4 Q = V[G]; 5 5 2 for each u Q key[u] = ; 14 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 while (Q not empty) 3 8 u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15 u

Prim’s Algorithm MST-Prim(G, w, r) What is the hidden cost in this code? Q = V[G]; A: DECREASE-KEY operation for each u Q key[u] = ; on the min-heap key[r] = 0; What will be the running time? p[r] = NULL; A: Depends on queue while (Q not empty) u = Extract. Min(Q); binary heap: O(E lg V) for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

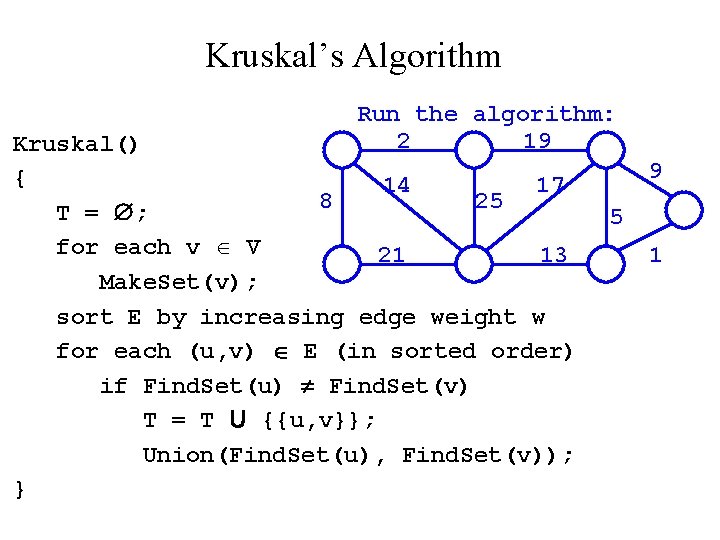
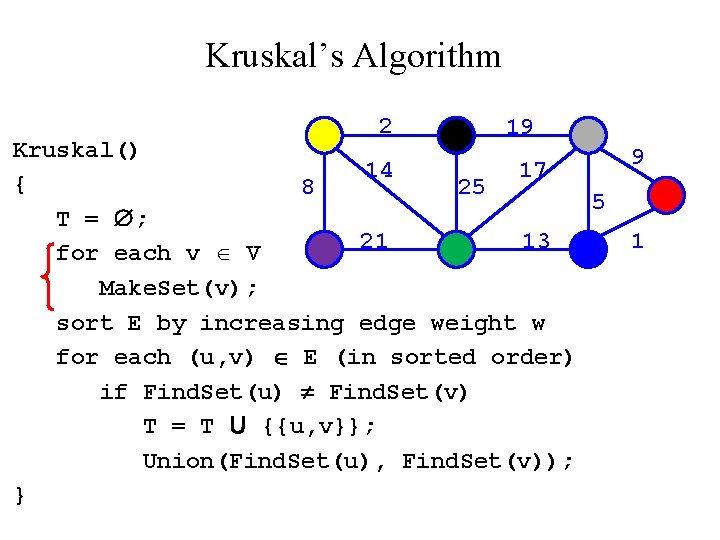
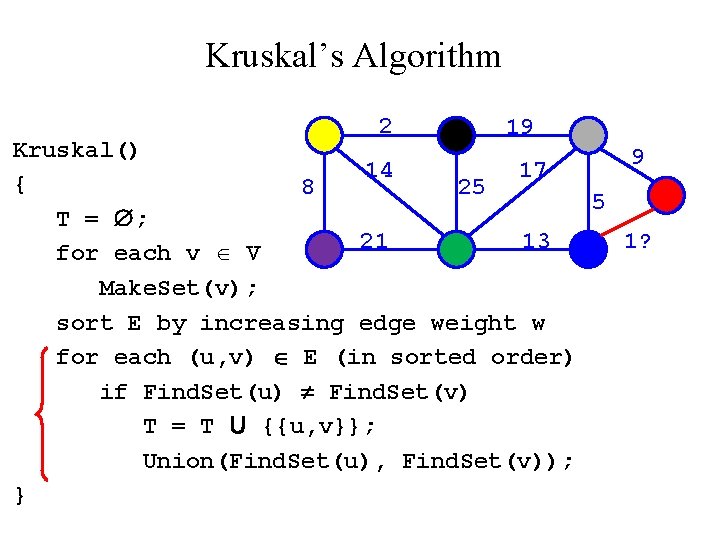
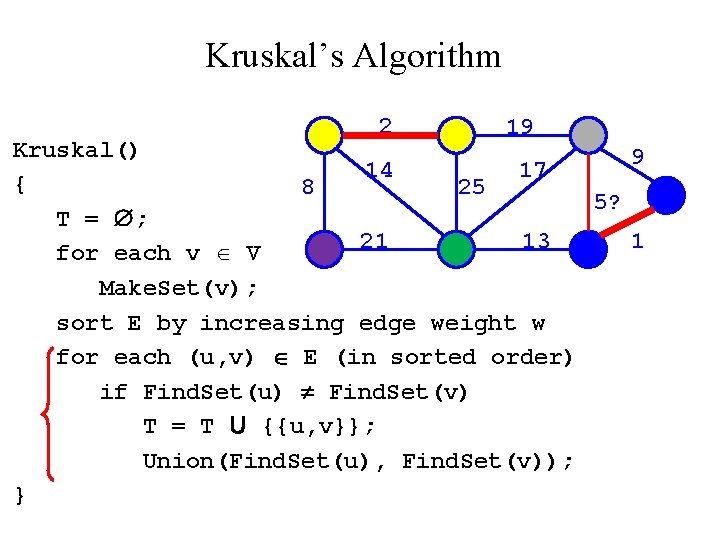
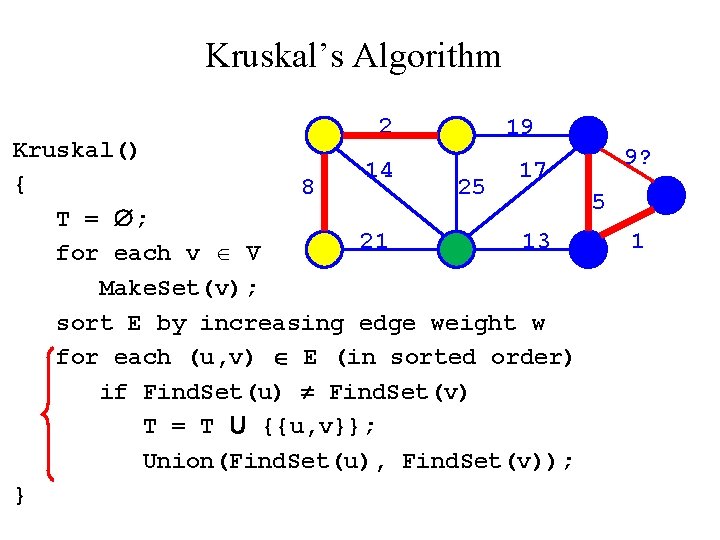
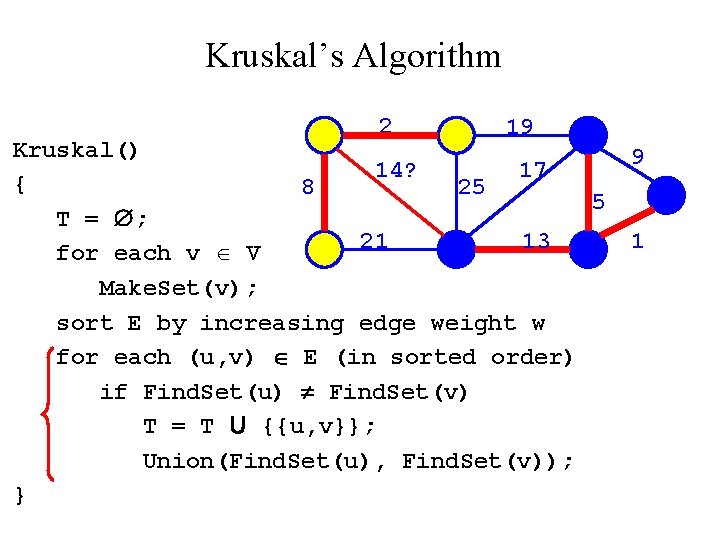
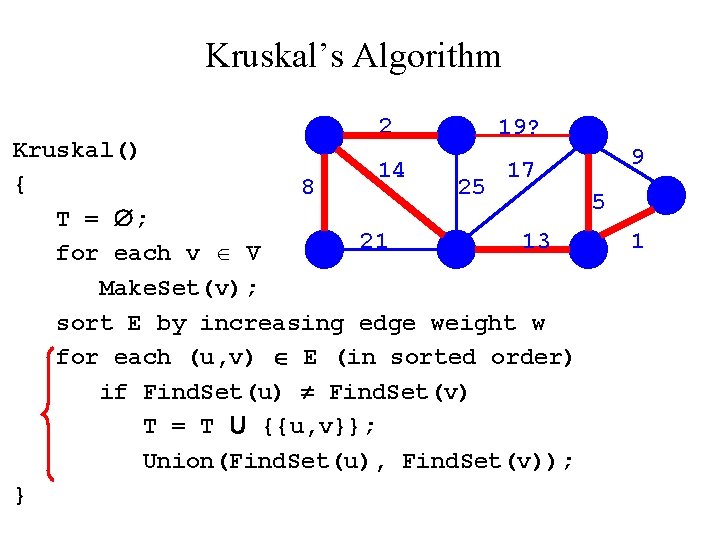
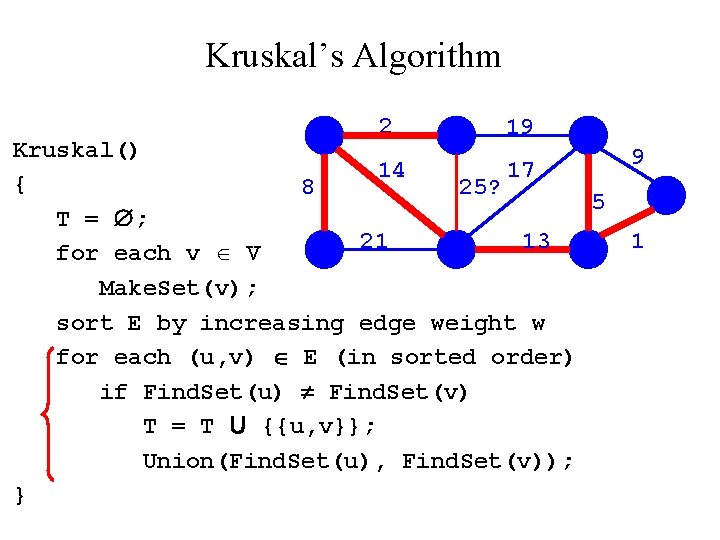
Kruskal’s Algorithm Run the algorithm: 2 19 Kruskal() { 14 17 8 25 T = ; for each v V 21 13 Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 5 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

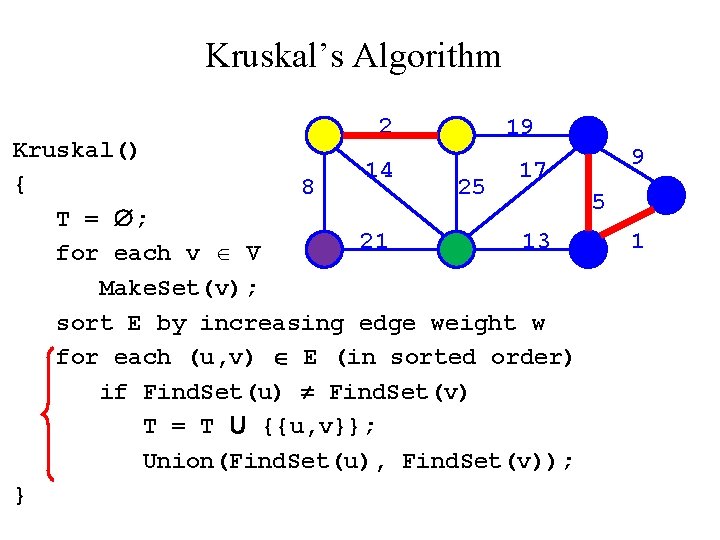
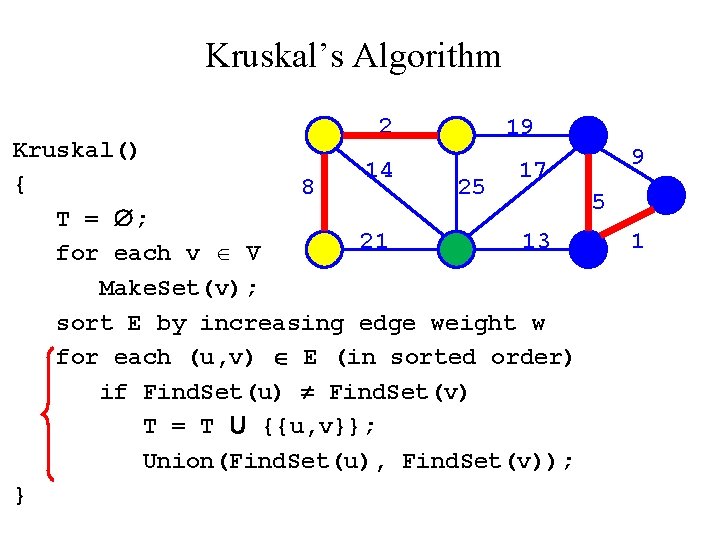
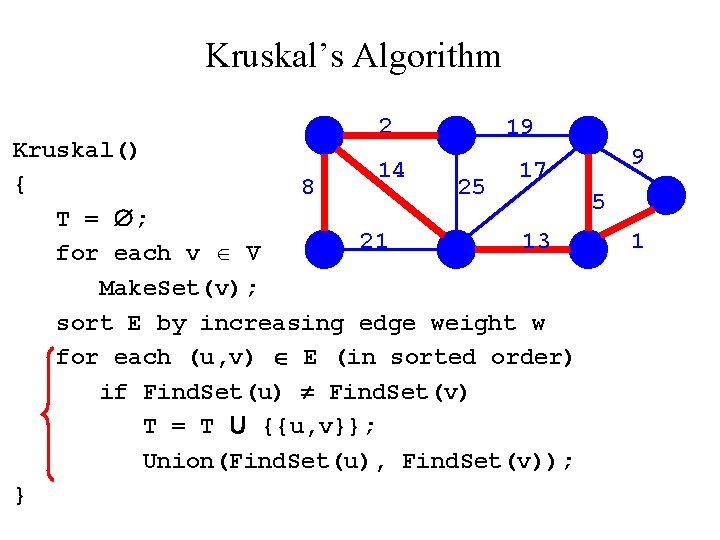
Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 9 14 17 { 8 25 5 T = ; 21 13 1? for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); }

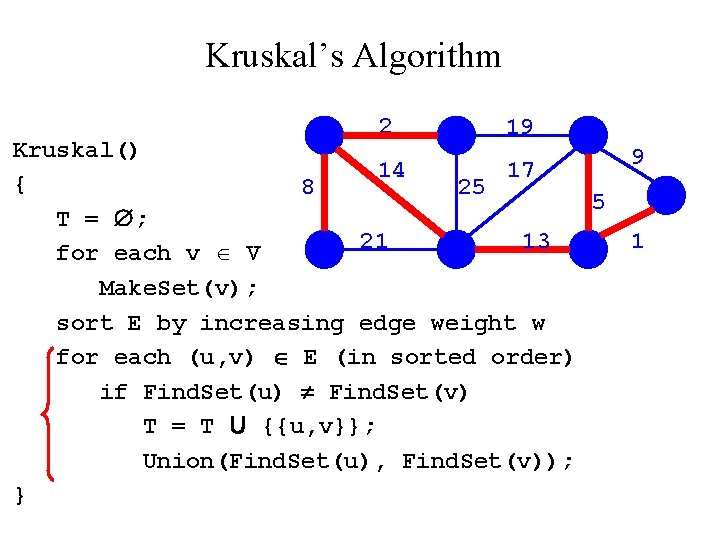
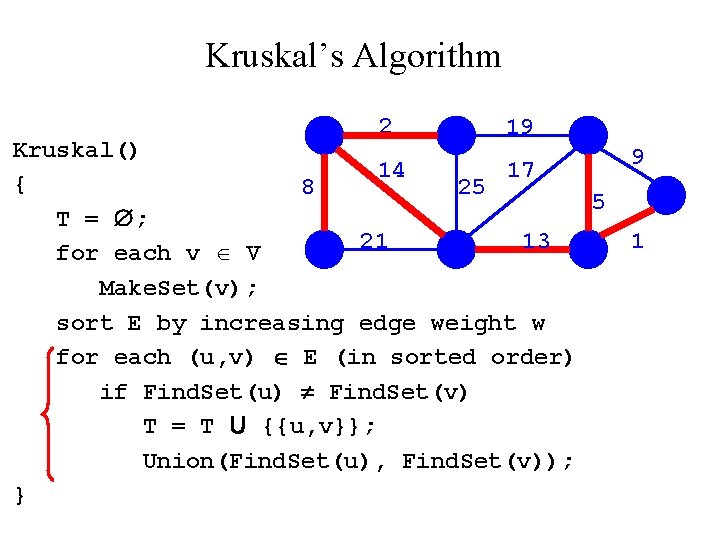
Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

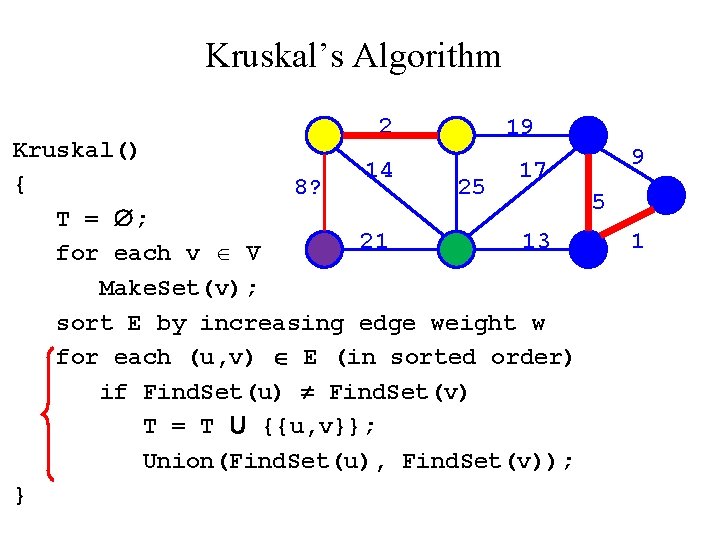
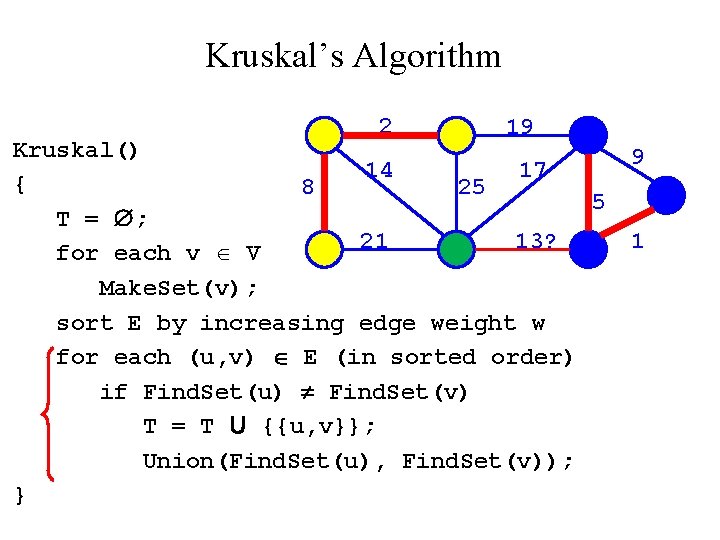
Kruskal’s Algorithm 2? 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

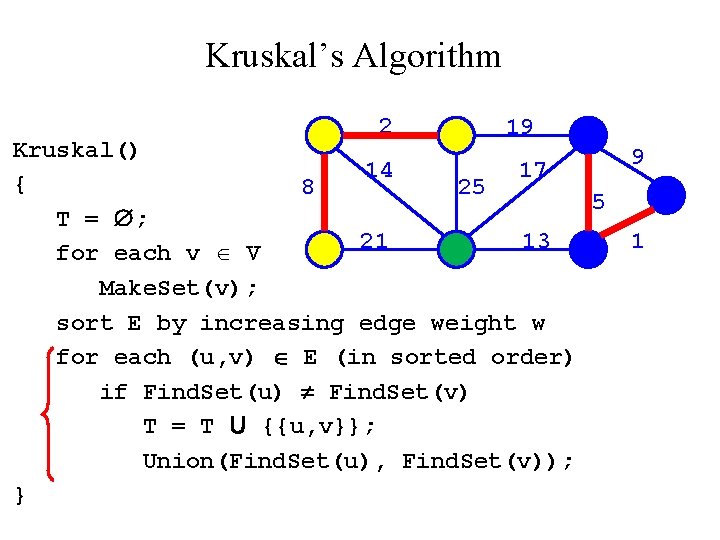
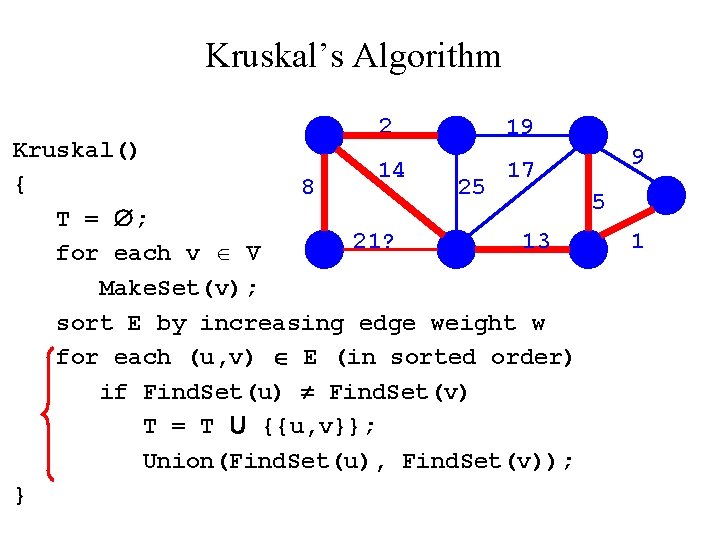
Kruskal’s Algorithm 2 19 Kruskal() 9 14 17 { 8 25 5? T = ; 21 13 1 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); }

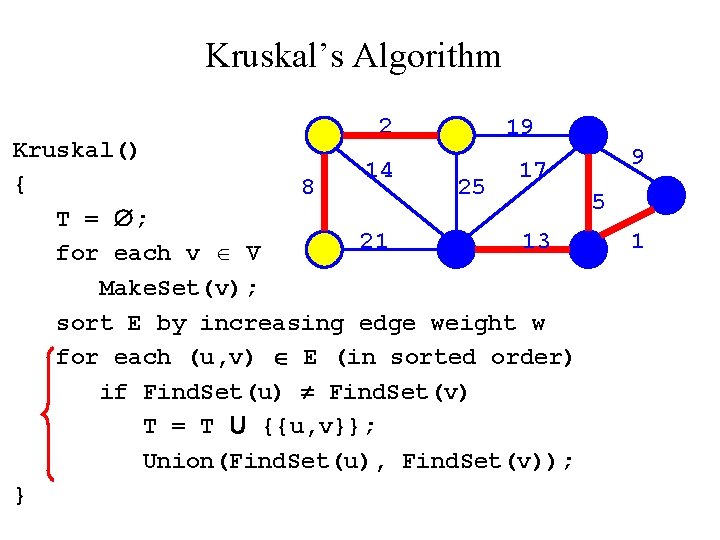
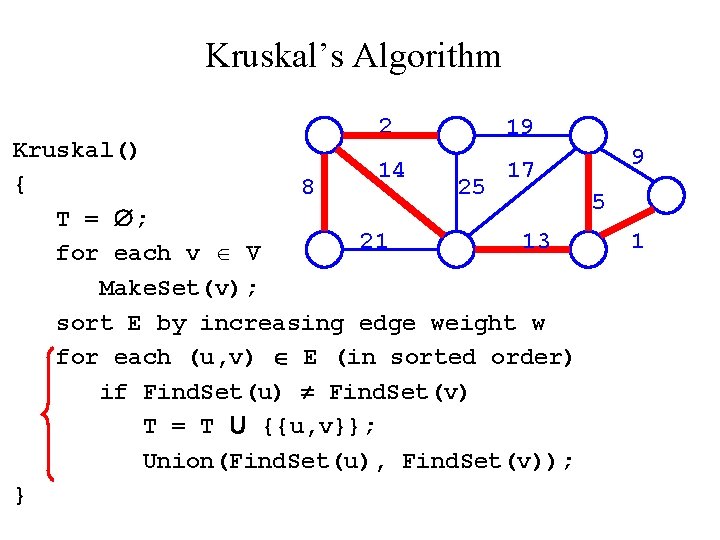
Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

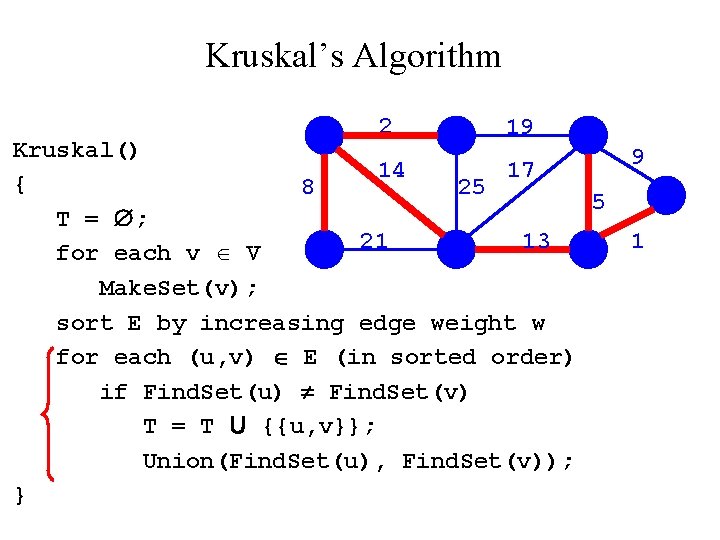
Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8? 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

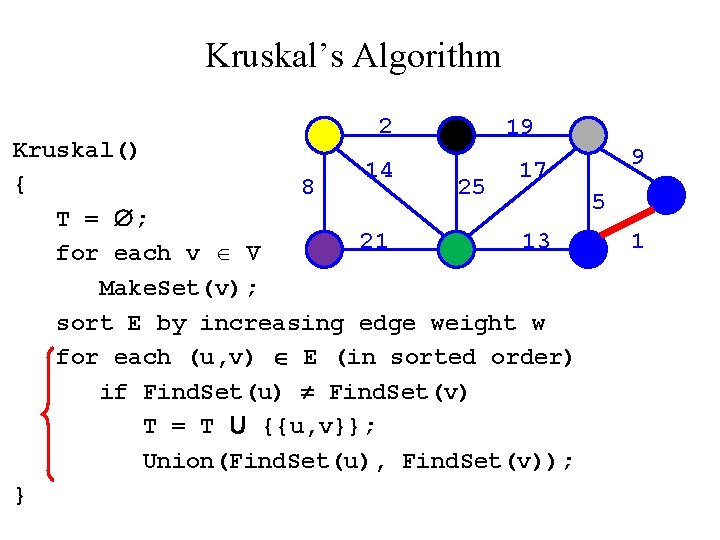
Kruskal’s Algorithm 2 19 Kruskal() 9? 14 17 { 8 25 5 T = ; 21 13 1 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); }

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13? for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

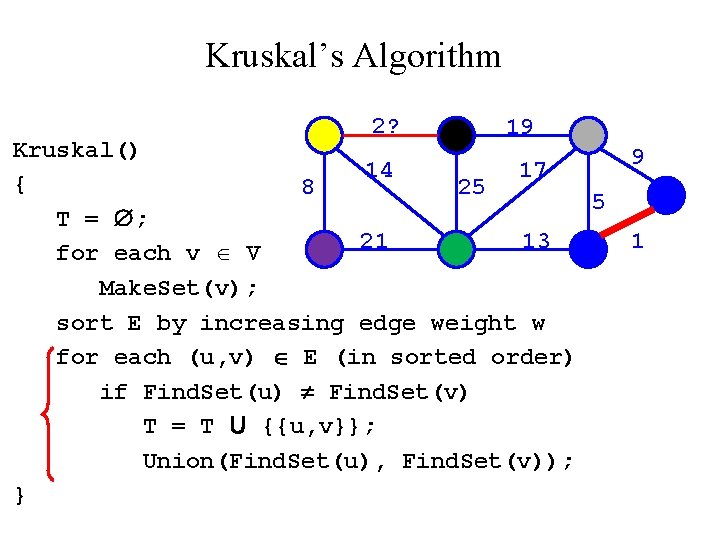
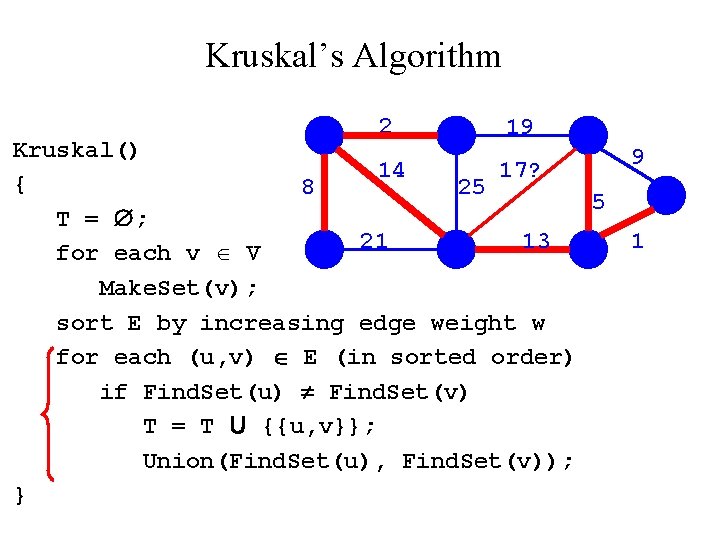
Kruskal’s Algorithm 2 19 Kruskal() 14? 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17? { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

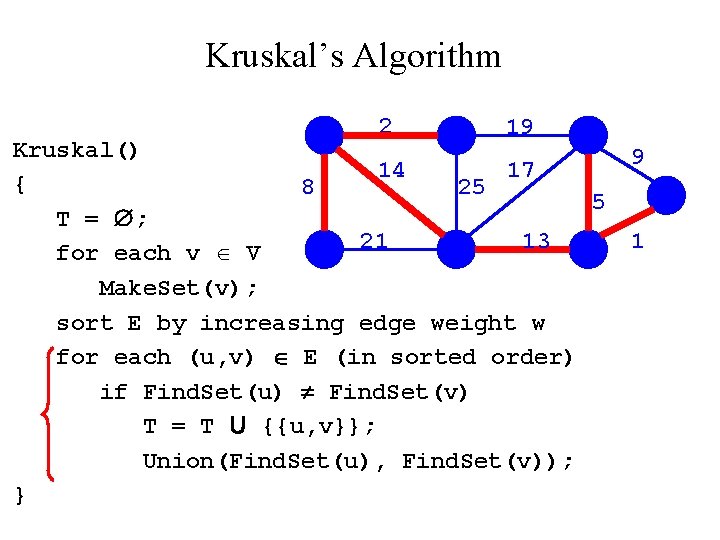
Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

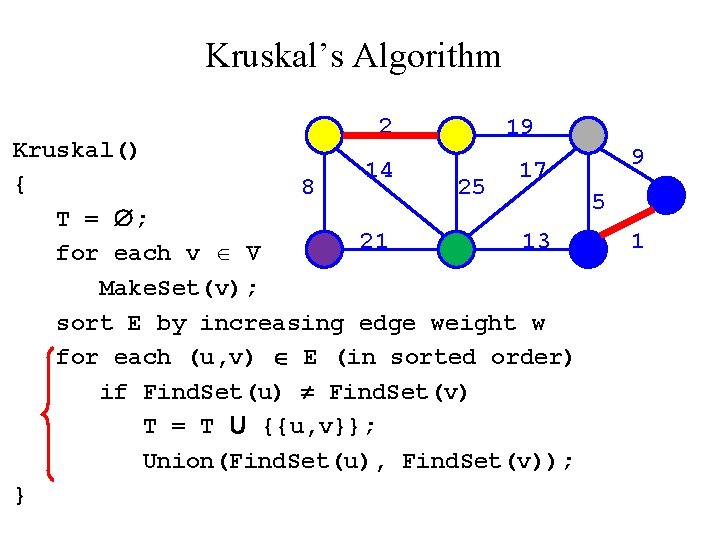
Kruskal’s Algorithm 2 19? Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21? 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25? 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Kruskal’s Algorithm 2 19 Kruskal() 14 17 { 8 25 5 T = ; 21 13 for each v V Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); } 9 1

Correctness Of Kruskal’s Algorithm • Sketch of a proof that this algorithm produces an MST for T: – Assume algorithm is wrong: result is not an MST – Then algorithm adds a wrong edge at some point – If it adds a wrong edge, there must be a lower weight edge – But algorithm chooses lowest weight edge at each step. Contradiction

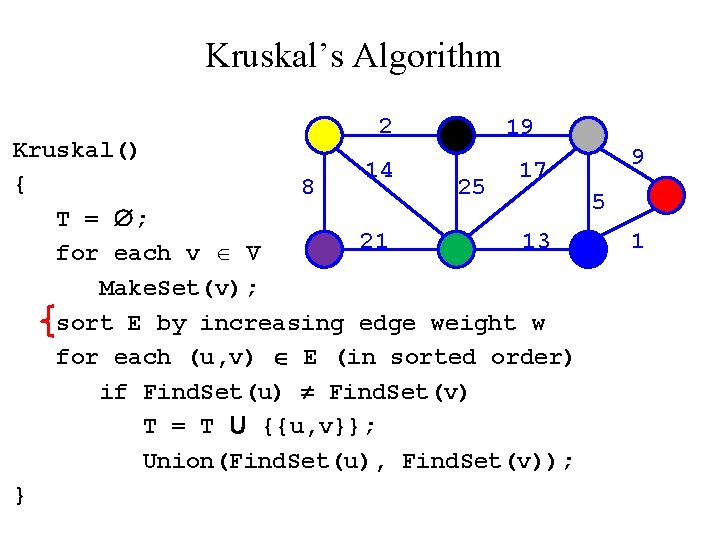
Kruskal’s Algorithm What will affect the running time? Kruskal() Sort { O(V) Make. Set() calls T = ; O(E) Find. Set() calls for each v V O(V) Union() calls Make. Set(v); sort E by increasing edge weight w for each (u, v) E (in sorted order) if Find. Set(u) Find. Set(v) T = T U {{u, v}}; Union(Find. Set(u), Find. Set(v)); }

Kruskal’s Algorithm: Running Time • To summarize: – – – Sort edges: O(E lg E) O(V) Make. Set()’s O(E) Find. Set()’s O(V) Union()’s Overall O(E lg E)

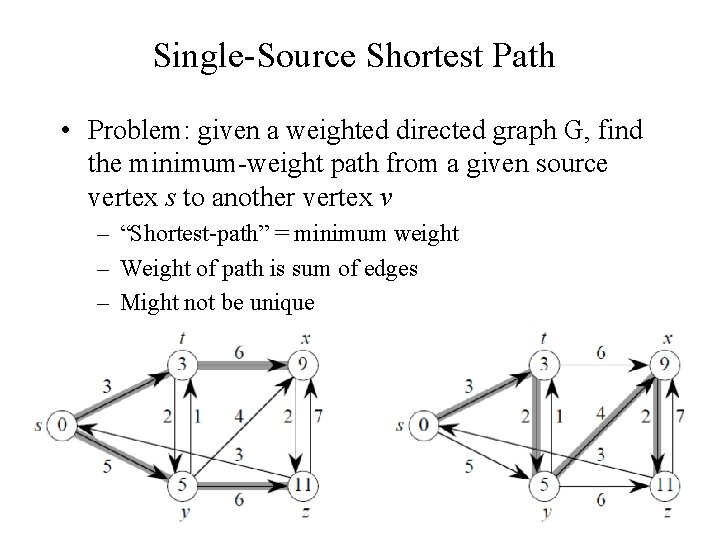
Single-Source Shortest Path • Problem: given a weighted directed graph G, find the minimum-weight path from a given source vertex s to another vertex v – “Shortest-path” = minimum weight – Weight of path is sum of edges – Might not be unique

Shortest Path Properties • Again, we have optimal substructure: the shortest path consists of shortest subpaths: – Proof: suppose some subpath is not a shortest path • There must then exist a shorter subpath • Could substitute the shorter subpath for a shorter path • But then overall path is not shortest path. Contradiction

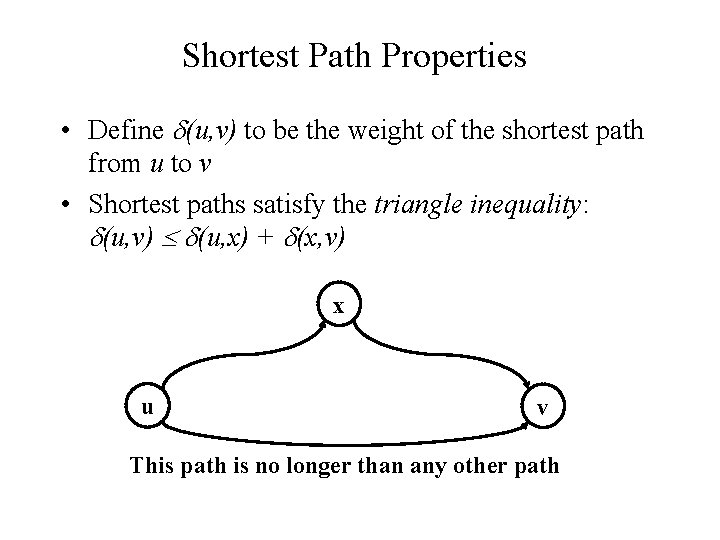
Shortest Path Properties • Define (u, v) to be the weight of the shortest path from u to v • Shortest paths satisfy the triangle inequality: (u, v) (u, x) + (x, v) x u v This path is no longer than any other path

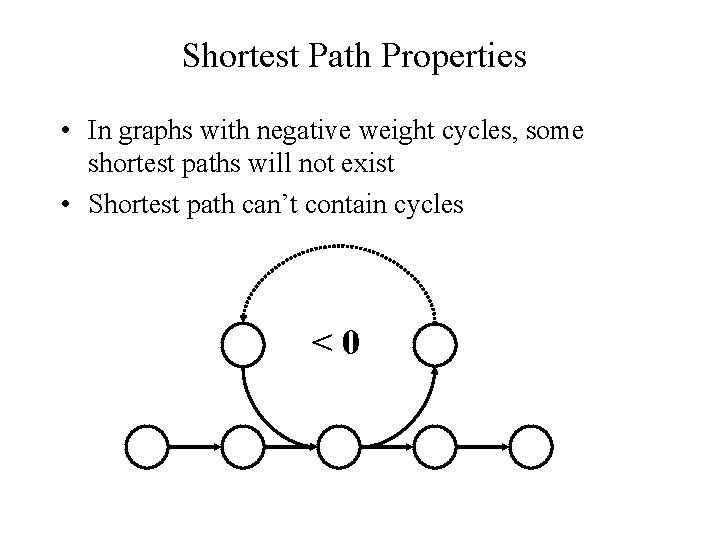
Shortest Path Properties • In graphs with negative weight cycles, some shortest paths will not exist • Shortest path can’t contain cycles <0

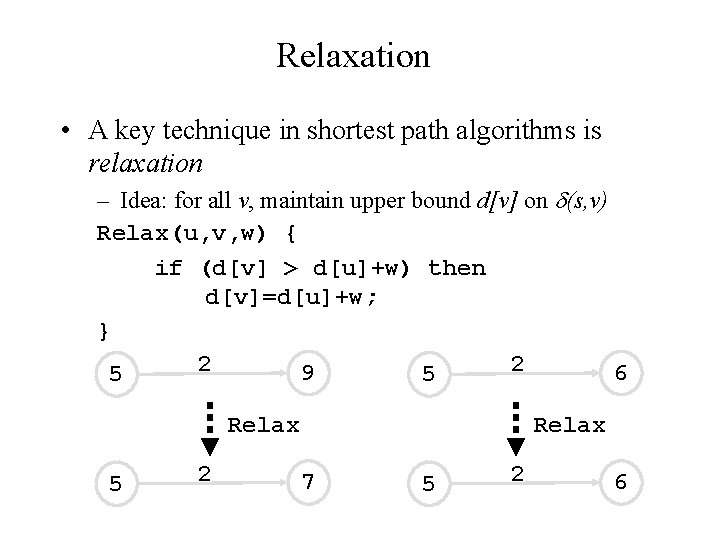
Relaxation • A key technique in shortest path algorithms is relaxation – Idea: for all v, maintain upper bound d[v] on (s, v) Relax(u, v, w) { if (d[v] > d[u]+w) then d[v]=d[u]+w; } 2 2 9 6 5 5 Relax 5 2 Relax 7 5 2 6

Bellman-Ford Algorithm Bellman. Ford() for each v V Initialize d[], which will converge to d[v] = ; shortest-path value d[s] = 0; for i=1 to |V|-1 Relaxation: for each edge (u, v) E Make |V|-1 passes, Relax(u, v, w(u, v)); relaxing each edge for each edge (u, v) E Test for solution: if (d[v] > d[u] + w(u, v)) have we converged yet? return “no solution”; i. e. , negative cycle? Relax(u, v, w): if (d[v] > d[u]+) then d[v]=d[u]+w

Bellman-Ford Algorithm Bellman. Ford() for each v V What will be the running time? A: O(VE) d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”;

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B A -1 0 3 2 2 1 4 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w E -3 D

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B -1 -1 A 0 3 1 4 4 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w 2 2 E -3 D

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B -1 -1 A 0 3 1 4 2 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w 2 2 E 1 -3 1 D

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B -1 -1 A 0 3 1 4 2 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w 2 2 E 1 -3 -2 D

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B -1 -1 A 0 3 1 4 2 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w 2 2 E 1 -3 -2 D

Bellman-Ford Algorithm Bellman. Ford() for each v V s d[v] = ; d[s] = 0; for i=1 to |V|-1 for each edge (u, v) E Relax(u, v, w(u, v)); for each edge (u, v) E if (d[v] > d[u] + w(u, v)) return “no solution”; B -1 -1 A 0 3 1 4 2 C 5 Relax(u, v, w): if (d[v] > d[u]+w) then d[v]=d[u]+w 2 2 E 1 -3 -2 D

Bellman-Ford Algorithm • Note that order in which edges are processed affects how quickly it converges • Correctness: show d[v] = (s, v) after |V|-1 passes

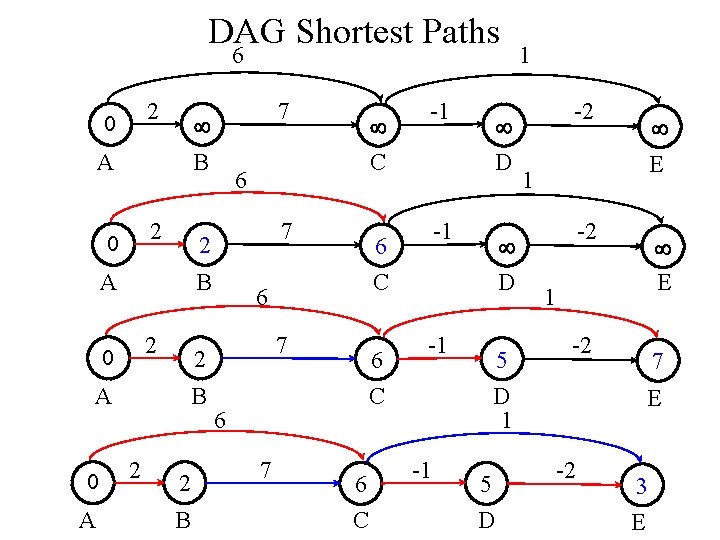
DAG Shortest Paths • Problem: finding shortest paths in DAG – Bellman-Ford takes O(VE) time. – How can we do better? – Idea: use topological sort DAG-Shortest-Paths(G, w, s) topologically sort the vertices for each v V d[v] = ; d[s] = 0; for each vertex u, taken in topologically sorted order for each vertex v Adj[u] Relax(u, v, w)

DAG Shortest Paths 6 2 0 B A 2 0 2 B 2 2 B -1 D -1 6 D C 6 7 2 A A 7 B 0 C 6 2 A 0 7 6 -1 5 7 6 C -2 E 1 -2 7 D 1 C 6 1 -1 5 D E -2 3 E

DAG Shortest Paths • Problem: finding shortest paths in DAG – Idea: use topological sort • If were lucky and processes vertices on each shortest path from left to right, would be done in one pass • Every path in a DAG is subsequence of topologically sorted vertex order, so processing verts in that order, we will do each path in forward order (will never relax edges out of vertices before doing all edges into vertices). • Thus: just one pass. • Time: O(V + E)

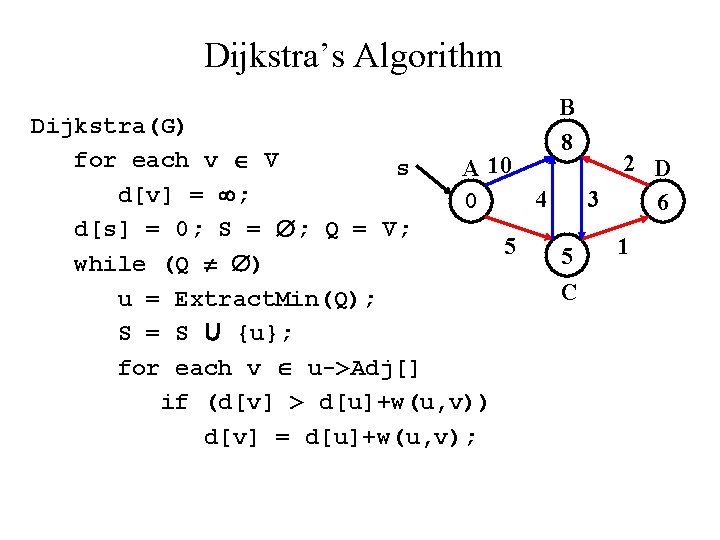
Dijkstra’s Algorithm • If no negative edge weights, Dijkstra’s essentially a weighted version of breadth-first search • Similar to breadth-first search – Grow a tree gradually, advancing from vertices taken from a queue • Also similar to Prim’s algorithm for MST – Use a priority queue keyed on d[v]

Dijkstra’s Algorithm B Dijkstra(G) for each v V 2 D A 10 d[v] = ; 4 3 d[s] = 0; S = ; Q = V; 5 1 while (Q ) C u = Extract. Min(Q); S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) Relaxation d[v] = d[u]+w(u, v); Step

Dijkstra’s Algorithm B Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 d[s] = 0; S = ; Q = V; 5 1 while (Q ) C u = Extract. Min(Q); S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

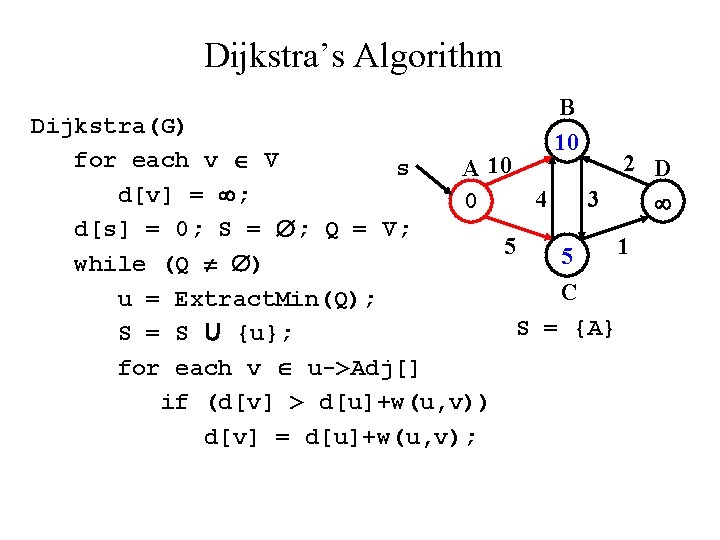
Dijkstra’s Algorithm B 10 Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 d[s] = 0; S = ; Q = V; 5 1 5 while (Q ) C u = Extract. Min(Q); S = {A} S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

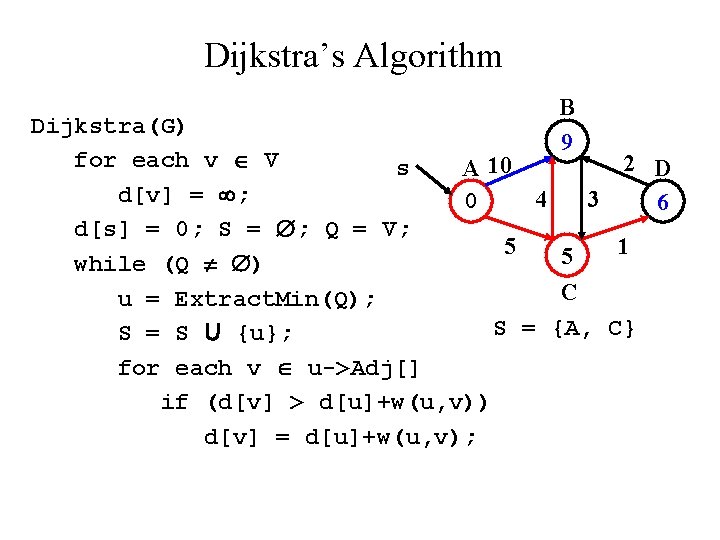
Dijkstra’s Algorithm B 9 Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 6 d[s] = 0; S = ; Q = V; 5 1 5 while (Q ) C u = Extract. Min(Q); S = {A, C} S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

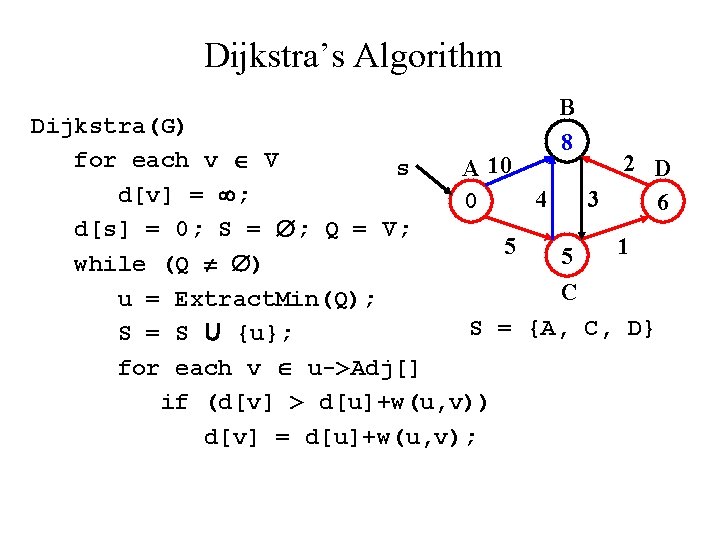
Dijkstra’s Algorithm B 8 Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 6 d[s] = 0; S = ; Q = V; 5 1 5 while (Q ) C u = Extract. Min(Q); S = {A, C, D} S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

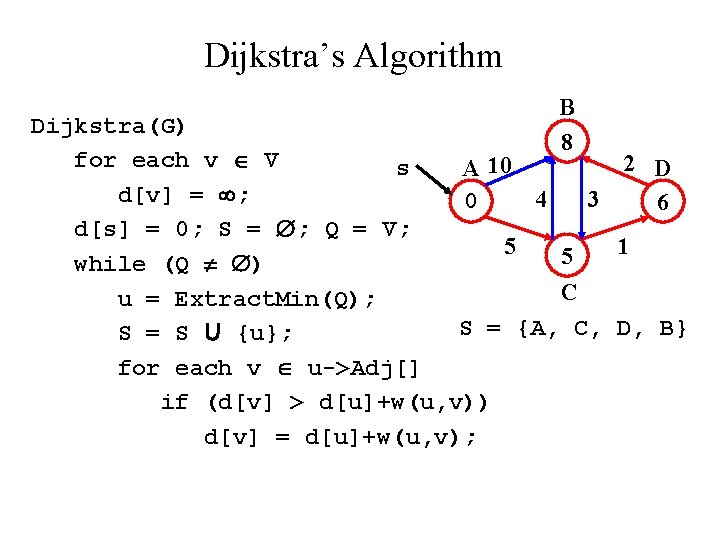
Dijkstra’s Algorithm B 8 Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 6 d[s] = 0; S = ; Q = V; 5 1 5 while (Q ) C u = Extract. Min(Q); S = {A, C, D, B} S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

Dijkstra’s Algorithm B 8 Dijkstra(G) for each v V 2 D s A 10 d[v] = ; 4 3 0 6 d[s] = 0; S = ; Q = V; 5 1 5 while (Q ) C u = Extract. Min(Q); S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v);

Dijkstra’s Algorithm Dijkstra(G) for each v V How many times is Extract. Min() called? d[v] = ; d[s] = 0; S = ; Q = V; while (Q ) How many times is u = Extract. Min(Q); Relax() called? S = S U {u}; for each v u->Adj[] if (d[v] > d[u]+w(u, v)) d[v] = d[u]+w(u, v); What will be the total running time? A: O(E lg V) using binary heap for Q