Derse giri iin tklayn Fonksiyonun Tarihi A Tanm

Derse giriş için tıklayın. . .

Fonksiyonun Tarihi A. Tanım B. Fonksiyonun Gösterimi C. Görüntü Kümesi A. Fonksiyon Çeşitleri 1. Bire Bir Fonksiyon 2. Örten Fonksiyon 3. İçine Fonksiyon 4. Birim (Özdeş) Fonksiyon 5. Sabit Fonksiyon ve Sıfır Fonksiyonu B. Eşit Fonksiyon C. Fonksiyon Sayısı D. Ters Fonksiyon E. Fonksiyonlarda Bileşke İşlemi ( Bileşke Fonksiyon ) F. Bileşke İşleminin Özellikleri

A. Tanım A ve B boş olmayan iki küme olsun. A nın her bir elemanını B de yalnız bir elemanla eşleyen f bağıntısına A dan B ye fonksiyon denir. A ya fonksiyonun tanım kümesi, B ye de fonksiyonun değer kümesi denir. x A ve y B olmak üzere A dan B ye bir f fonksiyonu f : A B veya x f(x) y biçiminde gösterilir. Örnek. . . 1 Örneği görmek için tıklayın A 1, 2, 3 ve B 1, 3, 4, 5, 9 kümeleri verilsin. A dan B ye bir f bağıntısı, f (x, y) : y x 2 biçiminde tanımlanıyor. y f(x) x 2 f(1) 12 1 f(2) 22 4 f(3) 32 9 olduğuna göre Tanım kümesi : A 1, 2, 3 Değer kümesi : B 1, 3, 4, 5, 6 f bağıntısı : f (1, 1), (2, 4), (3, 9) olur. Ana Menü İleri

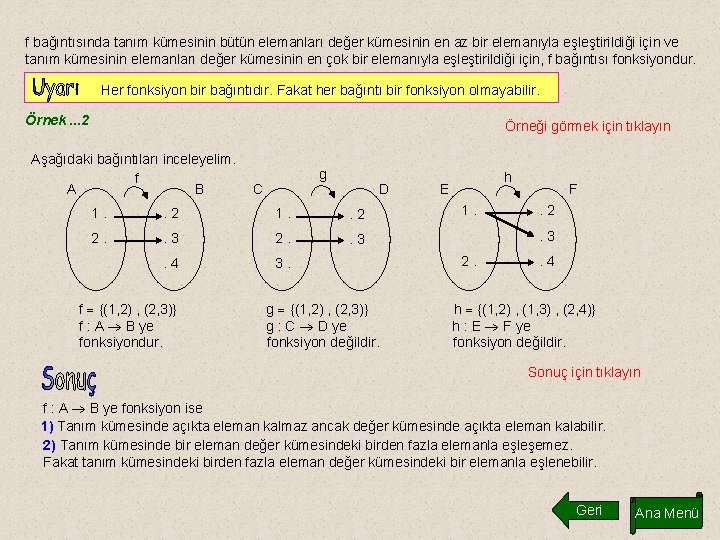
f bağıntısında tanım kümesinin bütün elemanları değer kümesinin en az bir elemanıyla eşleştirildiği için ve tanım kümesinin elemanları değer kümesinin en çok bir elemanıyla eşleştirildiği için, f bağıntısı fonksiyondur. Her fonksiyon bir bağıntıdır. Fakat her bağıntı bir fonksiyon olmayabilir. Örnek. . . 2 Örneği görmek için tıklayın Aşağıdaki bağıntıları inceleyelim. f A B g C D 1. . 2 2. . 3 . 4 3. f {(1, 2) , (2, 3)} f : A B ye fonksiyondur. g {(1, 2) , (2, 3)} g : C D ye fonksiyon değildir. h E 1. F. 2. 3 2. . 4 h {(1, 2) , (1, 3) , (2, 4)} h : E F ye fonksiyon değildir. Sonuç için tıklayın f : A B ye fonksiyon ise 1) Tanım kümesinde açıkta eleman kalmaz ancak değer kümesinde açıkta eleman kalabilir. 2) Tanım kümesinde bir eleman değer kümesindeki birden fazla elemanla eşleşemez. Fakat tanım kümesindeki birden fazla eleman değer kümesindeki bir elemanla eşlenebilir. Geri Ana Menü

B. Fonksiyonun Gösterimi Fonksiyonlar dört biçimde gösterilebilir. 1) Bağıntı ile 2) Liste yöntemi ile 3) Venn şeması ile 4) Grafik ile Örnek. . . 3 Örneği görmek için tıklayın A= {-2, 1, 2} B= {0, 1, 2, 3, 4} f(x)= x 2 -1 bağıntısı, tanım kümesi A ve değer kümesi B olan bir fonksiyondur. Fonksiyonun yukarıdaki gibi gösterimine bağıntı ile gösterim adı verilir. f(x)= x 2 -1 f(-2)=(-2)2 -1=3 f(1)=12 -1=0 f(2)=22 -1=3 olduğuna göre; f={(-2, 3), (1, 0), (2, 3)} gösterimine fonksiyonun liste yöntemi ile gösterimi adı verilir. Ana Menü İleri

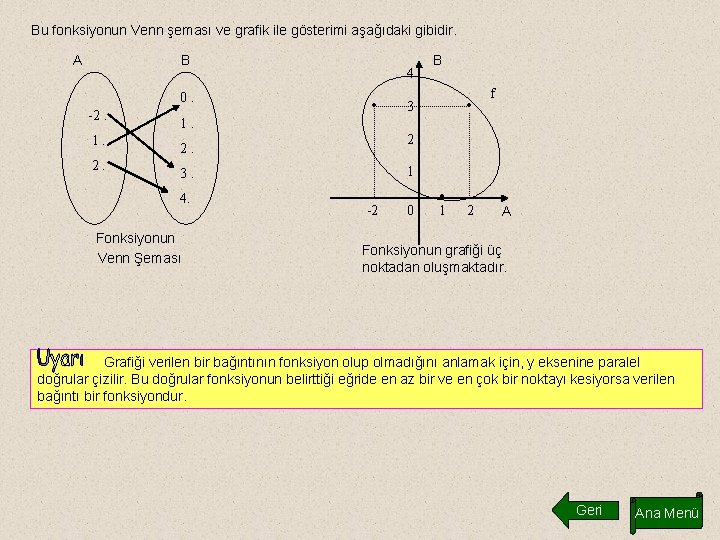
Bu fonksiyonun Venn şeması ve grafik ile gösterimi aşağıdaki gibidir. A B 0. -2. 1. 2. . 4 B . 3 f 1. 2 2. 1 3. 4. Fonksiyonun Venn Şeması -2 0 . 1 2 A Fonksiyonun grafiği üç noktadan oluşmaktadır. Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği eğride en az bir ve en çok bir noktayı kesiyorsa verilen bağıntı bir fonksiyondur. Geri Ana Menü

C. Görüntü Kümesi f : A B ye fonksiyon olsun. (x, y) f ise y = f(x)’e x in f fonksiyonu altındaki görüntüsü veya f nin x için değeri denir. Örnek. . . 4 A B 1. a. 2. b. 3. f(1) = a Örneği görmek için tıklayın Tanım kümesi: A = {1, 2, 3} f(2) = a Değer kümesi: B = {a, b, c, d} f(3) = c dir Görüntü kümesi= f(A) = {a, c} c. f fonksiyonu: f = {(1, a), (2, a), (3, c)} dir. d. Sonuç için tıklayın Görüntü kümesi değer kümesinin alt kümesidir. f: A B f(A) B dir. Ana Menü İleri

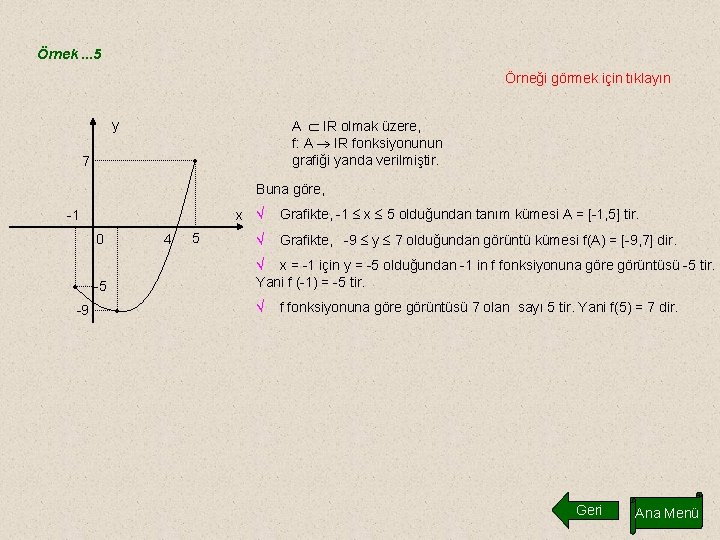
Örnek. . . 5 Örneği görmek için tıklayın y A IR olmak üzere, f: A IR fonksiyonunun grafiği yanda verilmiştir. . 7 Buna göre, x Ö -1 0 . -9 -5 4 . 5 Ö Grafikte, -1 x 5 olduğundan tanım kümesi A = [-1, 5] tir. Grafikte, -9 y 7 olduğundan görüntü kümesi f(A) = [-9, 7] dir. Ö x = -1 için y = -5 olduğundan -1 in f fonksiyonuna göre görüntüsü -5 tir. Yani f (-1) = -5 tir. Ö f fonksiyonuna göre görüntüsü 7 olan sayı 5 tir. Yani f(5) = 7 dir. Geri Ana Menü

A. Fonksiyon Çeşitleri 1. Bire Bir Fonksiyon f, A dan B ye bir fonksiyon olsun. f nin tanım kümesindeki her farklı elemanının görüntüsü farklı ise, f fonksiyonuna bire bir ( 1 -1 ) fonksiyon denir. A B 1. . 1 2. . 4 3. Yandaki Venn şeması ile gösterilen f fonksiyonu yukarıdaki tanıma uygun olduğundan bire bir fonksiyondur. . 9. 16 x 1, x 2 A için, f (x 1) = f (x 2) iken x 1 = x 2 ise, f fonksiyonu bire bir fonksiyondur. Ya da f (x 1) f (x 2) iken x 1 x 2 ise, f fonksiyonu bire birdir. Ana Menü İleri

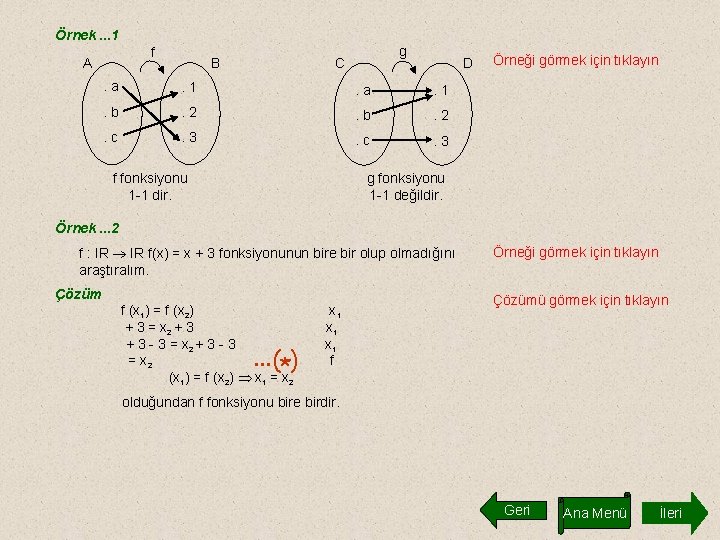
Örnek. . . 1 f A B g C D . a . 1 . b . 2 . c . 3 f fonksiyonu 1 -1 dir. Örneği görmek için tıklayın g fonksiyonu 1 -1 değildir. Örnek. . . 2 f : IR f(x) = x + 3 fonksiyonunun bire bir olup olmadığını araştıralım. Çözüm f (x 1) = f (x 2) + 3 = x 2 + 3 - 3 = x 2 (x 1) = f (x 2) x 1 = x 2 . . . (*) x 1 x 1 f Örneği görmek için tıklayın Çözümü görmek için tıklayın olduğundan f fonksiyonu bire birdir. Geri Ana Menü İleri

Örnek. . . 3 y y= x 2 -1 x -1 Örneği görmek için tıklayın Yandaki şekilde f : IR R, f (x) = x 2 - 1 fonksiyonunun bire bir olup olmadığını araştıralım. 1 0 -1 Çözüm y 2 y 1 y = x - 1 x x 1 x 2 0 -1 Çözümü görmek için tıklayın Şekilde tanım kümesindeki x 1 ve x 2 elemanları değer kümesindeki y 1 elemanıyla eşlenmiştir. Yani f(x 1) = f(x 2) ve x 1 x 2 ‘dir. Buna göre f : IR IR, f(x) = x 2 - 1 fonksiyonu bire bir değildir. Sonuç için tıklayın Grafiği verilen bir fonksiyonun bire bir olup olmadığını anlamak için Ox eksenine paralel doğru çizilir. Bu paralel doğrular grafiği bir noktada kesiyorsa fonksiyon bire birdir. Birden fazla noktada kesiyorsa fonksiyon bire bir değildir. Geri Ana Menü

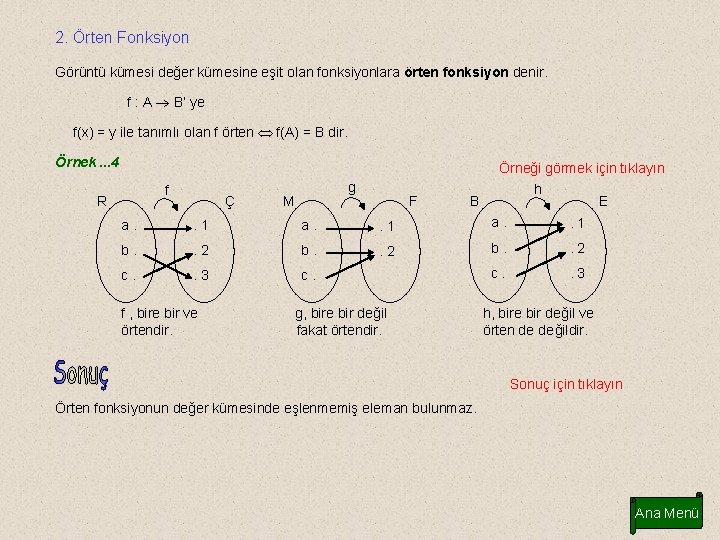
2. Örten Fonksiyon Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir. f : A B’ ye f(x) = y ile tanımlı olan f örten f(A) = B dir. Örnek. . . 4 f R Ç g M F B Örneği görmek için tıklayın h E a. . 1 b. . 2 c. . 3 f , bire bir ve örtendir. g, bire bir değil fakat örtendir. h, bire bir değil ve örten de değildir. Sonuç için tıklayın Örten fonksiyonun değer kümesinde eşlenmemiş eleman bulunmaz. Ana Menü

3. İçine Fonksiyon Görüntü kümesi değer kümesinin özalt kümesi olan fonksiyonlara içine fonksiyon denir. Kısaca, örten olmayan fonksiyonlara içine fonksiyon denir. Örnek. . . 5 Örneği görmek için tıklayın A = {-1, 0, 1} ve B = {0, 1, 2} olmak üzere, f : A B f(x) = x 2 Grafiği verilen bir fonksiyonun örten olup olmadığını anlamak için değer kümesi üzerinden Ox eksenine paraleller çizilir. Bu paraleller eğriyi daima kesiyorsa fonksiyon örtendir. Eğer çizilen paralellerden bazıları eğriyi kesmiyorsa fonksiyon içinedir. Fonksiyonunu inceleyelim. Çözüm f(x) = x 2 f(-1) = (-1)2 = 1 f(0) = 02 = 0 f(1) = 12 = 1 olduğuna göre, f(A) = {0, 1} dir. A f B -1. . 0 0. . 1 1. . 2 Çözümü görmek için tıklayın Değer kümesinde eşlenmemiş en az bir eleman olduğuna göre, f içinedir. Venn şemasından da görüldüğü gibi f, bire bir değil fakat içinedir. Ana Menü İleri

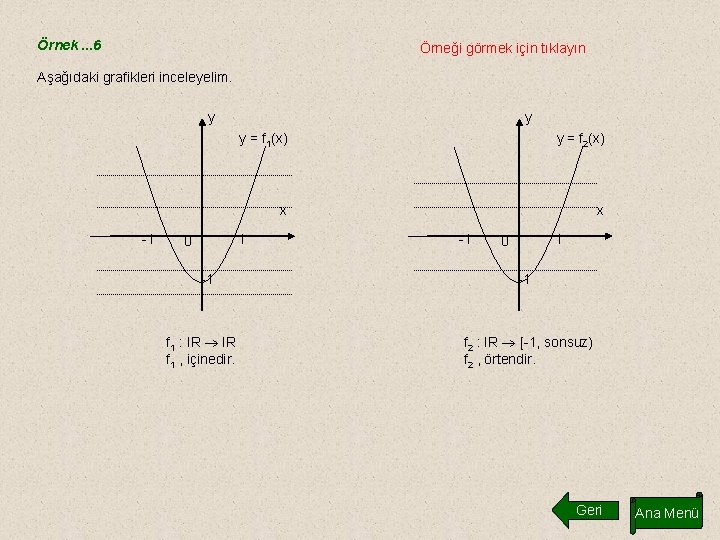
Örnek. . . 6 Örneği görmek için tıklayın Aşağıdaki grafikleri inceleyelim. y -1 y y = f 1(x) y = f 2(x) x x 1 0 -1 f 1 : IR f 1 , içinedir. -1 1 0 -1 f 2 : IR [-1, sonsuz) f 2 , örtendir. Geri Ana Menü

4. Birim (Özdeş) Fonksiyon Tanım kümesindeki her elemanın görüntüsü yine aynı ise bu tip fonksiyona birim fonksiyon denir ve ile gösterilir. f A B a. . a f: A B f(a) = a, f(b) = b, f(c) = c dir. Buna göre, f birim fonksiyondur. b. . b c. . c : A A, (x) = x veya f(x) fonksiyonu birim fonksiyondur. f, birim fonksiyon olduğuna göre, m. n. k kaçtır? Birim fonksiyon bire birdir. Çözümü görmek için tıklayın f, birim fonksiyon ise, f(x) = x tir. Buna göre, f(x) = (2 m - 4)x 2 + (2 n - 5)x + m + n + k dır. 0 1 f : IN+ f(x) = (2 m - 4)x 2 + (2 n - 5)x + m + n + k Çözüm Örneği görmek için tıklayın Örnek. . . 7 0 2 m - 4 = 0 m = 2. . . (1) 2 n - 5 = 1 n = 3. . . (2) m + n + k = 0 k = - m -n = -2 - 3 = -5. . . (3) m. n. n = 2. 3. (-5) = -30 dur. Ana Menü

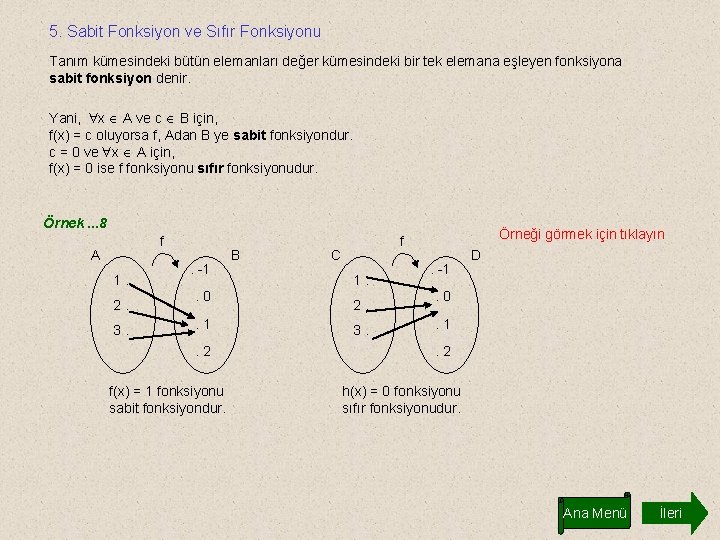
5. Sabit Fonksiyon ve Sıfır Fonksiyonu Tanım kümesindeki bütün elemanları değer kümesindeki bir tek elemana eşleyen fonksiyona sabit fonksiyon denir. Yani, x A ve c B için, f(x) = c oluyorsa f, Adan B ye sabit fonksiyondur. c = 0 ve x A için, f(x) = 0 ise f fonksiyonu sıfır fonksiyonudur. Örnek. . . 8 f A 1. 2. 3. . -1. 0. 1. 2 f(x) = 1 fonksiyonu sabit fonksiyondur. B Örneği görmek için tıklayın f C 1. 2. 3. . -1 D . 0. 1. 2 h(x) = 0 fonksiyonu sıfır fonksiyonudur. Ana Menü İleri

Örnek. . . 9 Örneği görmek için tıklayın f : IR f(x) = (m -1)x + 4 + m Fonksiyonu sabit fonksiyon olduğuna göre, f(8) kaçtır? Çözümü görmek için tıklayın Verilen f(x) fonksiyonu sabit fonksiyon olduğuna göre, x in katsayısı 0 olmalıdır. Buna göre, m - 1 = 0 m = 1 dir. Bu değer yerine yazılırsa, f(x) = (m - 1)x + 4 + m f(x) = (1 - 1)x + 4 + 1 f(x) = 0. X + 5 f(x) = 5 f(8) = 5 tir. Geri Ana Menü

B. Eşit Fonksiyon f : A B ve g : A B iki fonksiyon olsun. f ve g fonksiyonları A’nın her elemanı için aynı değeri alıyorsa f ve g’ye eşit fonksiyonlar denir ve f = g biçiminde gösterilir. Buna göre, f = g x A için f(x) = g(x) tir. Örnek. . . 10 Örneği görmek için tıklayın A = { -1, 0, 1 } B = { 0, 1, 2 } f : A B, f(x) = x + 1 g : A B, g(x) = x 3 + 1 biçiminde tanımlandığına göre, f = g olduğunu gösterelim. Çözümü görmek için tıklayın (x) = x + 1 f(-1) = -1 + 1 = 0 f(0) = 0 + 1 = 1 f(1) = 1 + 1 = 2 g(x) = x 3 + 1 g(-1) = (-1)3 + 1 = 0 g(0) = 03 + 1 = 1 g(1) = 13 + 1 =2 dir. x A için f(x) = g(x) olduğundan f = g dir. Ana Menü

C. Fonksiyon Sayısı s(A) = m s(B) = n olsun. 1. A’dan B’ye tanımlanabilen fonksiyonların sayısı : nm ‘dir. 2. B’den A’ya tanımlanabilen fonksiyonların sayısı : mn ‘dir. 3. A’dan B’ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı : 2 m. n - nm ‘dir. 4. A’dan B’ye tanımlanabilen bire bir fonksiyonların sayısı : n! 1. 2. 3. . . n dir. (n m) = (n-m)! 1. 2. 3. . . (n-m) 5. A’dan B’ye tanımlanabilen bire bir örten fonksiyonların sayısı : m! = 1. 2. 3. . . m dir. 6. A’dan A’ya tanımlanabilen içine fonksiyonların sayısı : mm -m! dir. 7. A’dan B’ye tanımlanabilen sabit fonksiyonların sayısı : n dir. Ana Menü İleri

Örnek. . . 11 Örneği görmek için tıklayın A = { 1, 2 } B = { a, b, c } kümeleri veriliyor. s(A) = 2 ve s(B) = 3 olduğuna göre, 1. A’dan B’ye tanımlanabilen fonksiyonların sayısı : 32 = 3. 3 = 9 dur. 2. B’den A’ya tanımlanabilen fonksiyonların sayısı : 23 = 2. 2. 2 = 8 dir. 3. A’dan B’ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı : 22. 3 - 32 = 26 - 9 = 55 tir. 4. A’dan B’ye tanımlanabilen bire bir fonksiyonların sayısı : 3! 1. 2. 3 = = 6 dır. (3 -2)! 1 5. A’dan A’ya tanımlanabilen içine fonksiyonların sayısı : 22 -2! = 4 - 1. 2 = 4 - 2 = 2 dir. 7. A’dan B’ye 3 tane sabit fonksiyon tanımlanabilir. Geri Ana Menü

D. Ters Fonksiyon f : A B ye bir ve örten bir fonksiyon olsun. f-1 : B A ya f nin ters fonksiyonu denir. f A B f: A B f(x) = y x. . y f -1(y) = x f -1 Örnek. . . 12 Örneği görmek için tıklayın A = { 1, 2, 3 } f: A B B = { 3, 6, 11 } f : x x 2 + 2 fonksiyonunun tersini liste yöntemiyle yazalım. Çözümü görmek için tıklayın f(x) = x 2 +2 f(1) = 12 + 2 = 3 f(2) = 22 + 2 = 6 f = {(1, 3), (2, 6), (3, 11)} f -1 = {(3, 1), (6, 2), (11, 3)} olur. f(3) = 32 + 2 = 11 Ana Menü İleri

Örnek. . . 13 Örneği görmek için tıklayın f: A B A = {a, b, c} B = {1, 2, 3} f 1 = {(a, 2), (b, 1), (c, 3)} f 1 -1 = {(2, a), (1, b), (3, c)} f 2 = {(a, 1), (b, 1), (c, 1)} f 2 -1 = {(1, a), (1, b), (1, c)} Burada f 1 in tersi olan f 1 -1 fonksiyondur. f 2 nin tersi olan f 2 -1 bağıntısı fonksiyon değildir. Sonuç için tıklayın Her fonksiyonun tersi, bir fonksiyon olmayabilir. f bire bir ve örten değilse f bağıntısı fonksiyon değildir. -1 y = f(x) biçimindeki bir f fonksiyonunun tersini bulmak için x yalnız bırakılır. Tanım ve değer kümeleri yer değiştirdiğinden x ile y nin değerleri değiştirilir. Geri Ana Menü İleri

Örnek. . . 14 Örneği görmek için tıklayın f : - 1, ) 4, ) f(x) = x 2 + 2 x + 5 olduğuna göre f -1(5) kaçtır? A) 2 B) 1 C) 0 D) -1 E) -2 Çözümü görmek için tıklayın f -1(5) = k f(k) = 5 k değeri f nin tanım kümesindeki bir değerdir. f nin tanım kümesi - 1, ) olduğunda bu aralıkta -2 yoktur. k 2 + 2 k + 5 = 5 k 2 + 2 k = 0 O halde f -1(5) = 0 dır. k(k + 2) = 0 Cevap C k = 0 veya k + 2 = 0 k = 0 veya k = -2 dir. Sonuç için tıklayın 1. ) f : IR IR, f(x) = ax + b f -1(x) = d a 2. ) f : IR c c { f(x) = } { x-b a } -dx + b ax + b f -1(x) = dır. cx - a cx + d Geri Ana Menü İleri

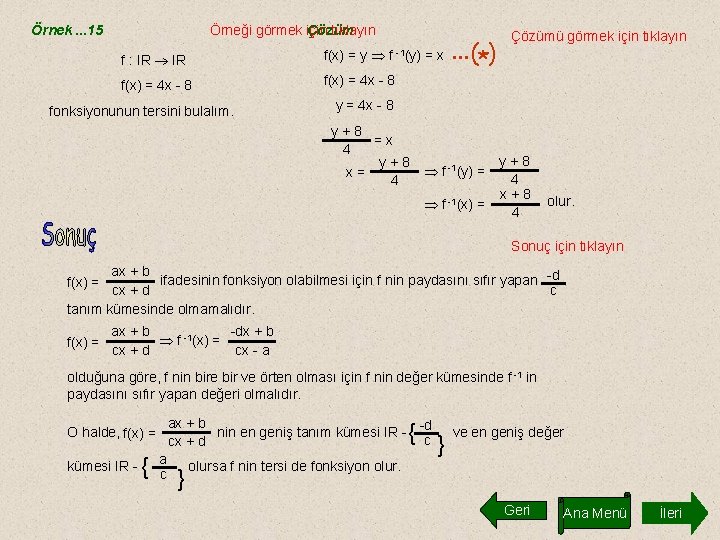
Örnek. . . 15 Örneği görmek için Çözüm tıklayın f : IR f(x) = y f f(x) = 4 x - 8 fonksiyonunun tersini bulalım. -1(y) =x . . . (*) Çözümü görmek için tıklayın y = 4 x - 8 y+8 =x 4 y+8 x= 4 f -1(y) = f -1(x) = y+8 4 x+8 4 olur. Sonuç için tıklayın ax + b ifadesinin fonksiyon olabilmesi için f nin paydasını sıfır yapan -d cx + d c tanım kümesinde olmamalıdır. f(x) = -dx + b ax + b f -1(x) = cx - a cx + d olduğuna göre, f nin bire bir ve örten olması için f nin değer kümesinde f -1 in paydasını sıfır yapan değeri olmalıdır. ax + b nin en geniş tanım kümesi IR - -d c cx + d { O halde, f(x) = kümesi IR - { a c } } ve en geniş değer olursa f nin tersi de fonksiyon olur. Geri Ana Menü İleri

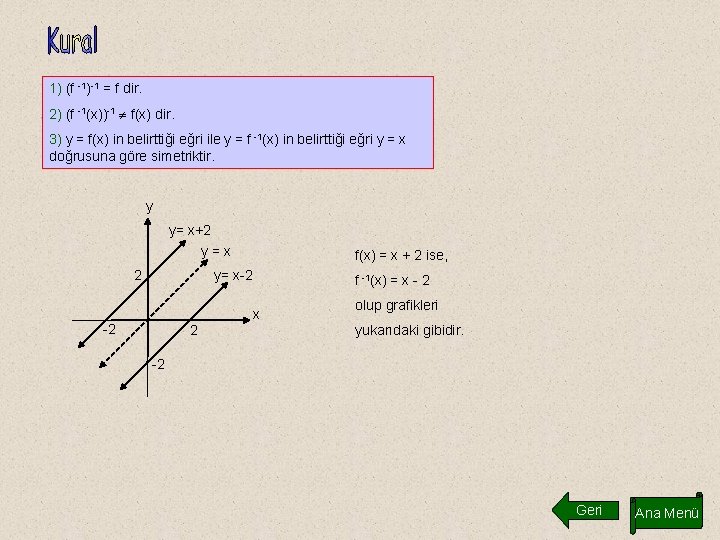
1) (f -1)-1 = f dir. 2) (f -1(x))-1 f(x) dir. 3) y = f(x) in belirttiği eğri ile y = f -1(x) in belirttiği eğri y = x doğrusuna göre simetriktir. y y= x+2 2 y=x . . -2 f(x) = x + 2 ise, y= x-2 . 2 f -1(x) = x - 2 x olup grafikleri yukarıdaki gibidir. Geri Ana Menü

E. Fonksiyonlarda Bileşke İşlemi ( Bileşke Fonksiyon ) A, B, C birer küme olsun. f : A B, f(x) = z g : B C, f(z) = y ise gof : A C, (gof)(x) = g f(x) = y kuralı ile tanımlı fonksiyona f ile g nin bileşke fonksiyonu denir. A x. f B . z g C . y gof Ana Menü İleri

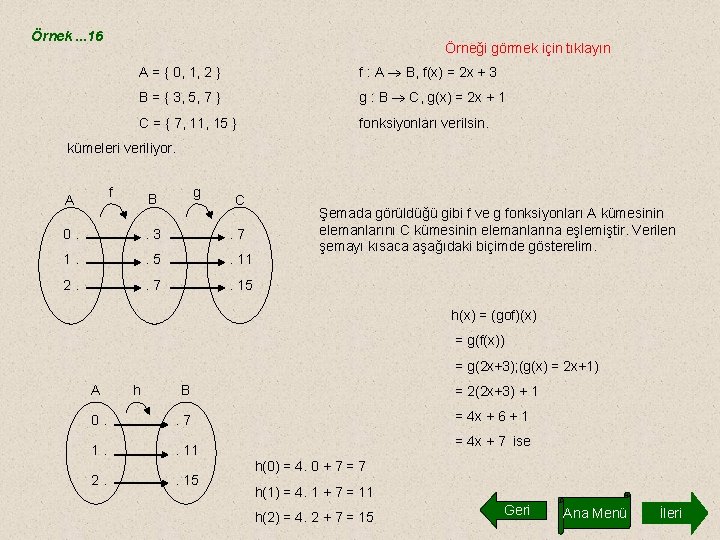
Örnek. . . 16 Örneği görmek için tıklayın A = { 0, 1, 2 } f : A B, f(x) = 2 x + 3 B = { 3, 5, 7 } g : B C, g(x) = 2 x + 1 C = { 7, 11, 15 } fonksiyonları verilsin. kümeleri veriliyor. f A g B C 0. . 3 . 7 1. . 5 . 11 2. . 7 . 15 Şemada görüldüğü gibi f ve g fonksiyonları A kümesinin elemanlarını C kümesinin elemanlarına eşlemiştir. Verilen şemayı kısaca aşağıdaki biçimde gösterelim. h(x) = (gof)(x) = g(f(x)) = g(2 x+3); (g(x) = 2 x+1) A h B 0. . 7 1. . 11 2. . 15 = 2(2 x+3) + 1 = 4 x + 6 + 1 = 4 x + 7 ise h(0) = 4. 0 + 7 = 7 h(1) = 4. 1 + 7 = 11 h(2) = 4. 2 + 7 = 15 Geri Ana Menü İleri

Örnek. . . 17 Örneği görmek için tıklayın f : IR IR, f(x) = 4 x + 5 g : IR IR, g(x) = 3 x - 2 fonksiyonları tanımlanıyor. Buna göre, (fog)(x) ve (gof)(x) fonksiyonlarını bulalım. Çözümü görmek için tıklayın (fog)(x) = f(g(x)) (gof)(x) = g(f(x)) = f(3 x - 2) = g(4 x + 5) = 4(3 x - 2) + 5 = 3(4 x + 5) - 2 = 4. 3 x - 4. 2 + 5 = 3. 4 x + 3. 5 - 2 = 12 x - 3 = 12 x + 13 . . . (*) Geri Ana Menü

F. Bileşke İşleminin Özellikleri 1. Bileşke işleminin değişme özelliği yoktur. fog gof 2. Bileşke işleminin birleşme özelliği vardır. fo(goh) = (fog)oh = fogoh 3. I(x) = x olmak üzere, fo. I = Iof = f olduğu için, I(x) = x fonksiyonuna bileşke işleminin birim ( etkisiz ) elemanı denir. 4. fof -1 = f -1 of = I dır. Buna göre, f nin bileşke işlemine göre tersi f -1 dir. 5. (fog) -1 = g -1 of -1 dir. Örnek. . . 18 Örneği görmek için tıklayın Çözümü görmek için tıklayın (fog)(x) = x 2 - 2 x + 1 f(x) = x + 4 f(g(x)) = x 2 - 2 x + 1 ve f(x) = x + 4 ise, olduğuna göre g(x) fonksiyonunu bulalım. g(x) + 4 = x 2 - 2 x + 1 g(x) = x 2 - 2 x + 1 - 4 g(x) = x 2 - 2 x - 3 olur. Ana Menü İleri

Örnek. . . 19 Örneği görmek için tıklayın (fof)(x) = 4 x + 3 olduğuna göre, f(x) fonksiyonunu bulalım. Çözümü görmek için tıklayın (fof)(x) = 4 x + 3. . . ( ) olduğuna göre, f(x) fonksiyonu ax + b biçimindedir. f(x) = ax + b olsun. a = 2 için, ab + b = 3 (fof)(x) = f(f(x)) 2 b + b = 3 = f(ax + b) 3 b = 3 = a(ax + b) + b = ( ) ve ( a 2 x + ab + b. . . ( ) b = 1 dir. a = -2 için, ab+ b = 3 ) eşitliğinden, -2 b + b = 3 4 x + 3 = a 2 x + ab + b ( 4 = a 2 ve 3 = ab + b ) -b = 3 a 2 = 4 ( a = 2 veya a = -2 ) dir. b = -3 tür. Buna göre, f(x) = ax + b fonksiyonu f(x) = 2 x + 1 veya f(x) = -2 x - 3 olur. Geri Ana Menü İleri

Örnek. . . 20 Örneği görmek için tıklayın f(x) = 2 x - 4 x+4 2 (fog -1) -1 = (g -1) -1 of -1 = gof -1 olduğuna göre, g(3) kaçtır? B) 10 Çözümü görmek için tıklayın f(x) = 2 x - 4 f -1(x) = (fog -1) -1(x) = 3 x + 6 A) 12 Çözüm C) 8 D) 6 . . . (*) E) 2 Buna göre, (fog -1) -1(x) = 3 x + 6 ( gof -1)(x) = 3 x + 6 g(f -1(x)) = 3 x + 6 g ( x+4 2 ) = 3 x + 6 olur. g(3) ün bulunabilmesi için x+4 yi 3 e eşitleyen x değeri bulunmalıdır. 2 x+4 = 3 x + 4 = 6 x = 2 dir. 2 ( g( O halde, g x+4 2 2+4 2 ) = 3 x + 6 ) = 3. 2 + 6 g ( 26 ) = 6 + 6 g(3) = 12 olur. Cevap A Geri Ana Menü İleri

Örnek. . . 21 y = g(x) . 10 3 . -2 Örneği görmek için tıklayın Şekilde f doğrusal fonksiyonu ile g fonksiyonunun grafikleri verilmiştir. . 0 Buna göre, (f -1 og)(1) + (fog -1)(3) kaçtır? . 1 . 5 A) 9 B) 10 C) 11 D) 12 E) 13 y = f(x) Çözümü görmek için tıklayın Şekildeki grafiğe göre, g(1) in sonucu m ise, f(1) in sonucu da m dir. Buna göre, f(1) = m f -1(m) = 1 dir. (f -1 og)(1) = f -1(g(1)) = f -1(m) = 1 g fonksiyonu (0, 3) noktasından geçtiğine göre, g(0) = 3 g-1(3) = 0 f fonksiyonu (0, 10) noktasından geçtiğine göre, Cevap C f(0) = 10 O halde, (f -1 og)(1) + (fog -1)(3) = f -1(g(1)) + f(g-1(3)) = 1 + f(0) = 1 + 10 = 11 dir. Geri Ana Menü İleri

f fonksiyonu ile g fonksiyonu (a, b) noktasında kesişiyorlarsa (f -1 og)(a) = a ve (f og -1)(b) = b olur. Örnek. . . 22 Örneği görmek için tıklayın f(x) = x 2 - 2 x + 3 olduğuna göre, f(1 - x) - f(x - 1) aşağıdakilerden hangisine eşittir? A) -2 x + 3 B)2 x - 3 C) 4 x + 4 D) 0 E) 4 x - 4 Çözümü görmek için tıklayın f(x) = x 2 - 2 x + 3 f(1 -x) = (1 -x)2 - 2(1 -x) + 3 = 1 - 2 x + x 2 - 2 + 2 x + 3 = x 2 + 2. . . ( ) f(x-1) = (x-1)2 - 2(x-1) + 3 = x 2 - 2 x + 1 - 2 x + 2 + 3 = x 2 - 4 x + 6. . . ( ) ve ( ) den f(1 -x) - f(x-1) = x 2 + 2 - (x 2 - 4 x + 6) = x 2 + 2 - x 2 + 4 x - 6 = 4 x + 2 - 6 = 4 x - 4 olur. Geri Cevap E Ana Menü İleri

Örnek. . . 23 Örneği görmek için tıklayın f : IR f(x) = (x+2). f(x+3) f(7) = A) 1 B) 2 C) 3 D) 4 E) 5 1 6 olduğuna göre, f(1) kaçtır? Çözüm 1 f(x) = (x+2). f(x+3) ve f(7) = 6 x = 4 için, f(4) = (4+2). f(4+3) Çözümü görmek için tıklayın ise, f(4) = 6. f(7) f(4) = 6. 1 6 f(4) = 1 x= 1 için, f(1) = (1+2). f(1+3) f(1) = 3. f(4) f(1) = 3. 1 f(1) = 3 tür. Cevap C Geri İleri

Fonksiyonun Tarihi Fonksiyon; bir cümlenin (kümenin) her elemanını ikinci bir cümlenin yalnız bir elemanıyla eşleyen bir bağıntı. Birinci cümleye tanım cümlesi, ikinci cümleye değer cümlesi denir. Genellikle bu elemanlar sayılardan ibarettir. Pekçok fonksiyon, çeşitli bilim konularından ortaya çıkar. Fonksiyon 17. yüzyıldan beri matematiğin bir ana kavramı olmuştur. Hareketlerin araştırılmasında Galile, Kepler ve Newton, zamanla mesafe arasında münasebetleri ortaya koymuşlardır. Gazların sıcaklık, basınç ve hacimleri arasındaki münasebet Robert Boyle tarafından 17. yüzyılda ve A. C. Charles tarafından 18. yüzyılda keşfedilmiştir. 19. Yüzyılda ise akım, voltaj ve direnç arasındaki münasebet ile elektrik anlaşılır hale gelmiştir. Daha sonra biyoloji ve sosyal ilimlerde de sayılar ile ilgili bilgiler ve bununla fonksiyon kavramı önem kazanmıştır. Bilimde en önemli kavramın değişkenler arasındaki ilişkiler olduğu söylenebilir. Ana Menü