Dorusal Fonksiyonlar Karesel Fonksiyonlar Polinomlar ve Rasyonel Fonksiyonlar

Doğrusal Fonksiyonlar, Karesel Fonksiyonlar, Polinomlar ve Rasyonel Fonksiyonlar, Fonksiyon Çizimleri

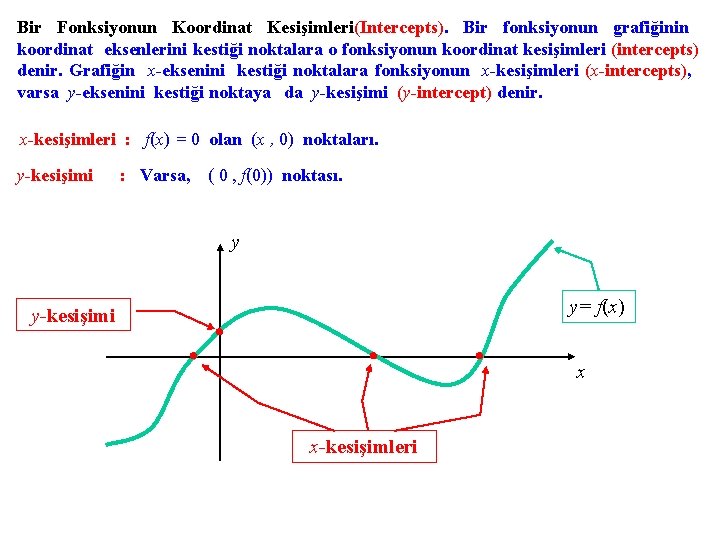
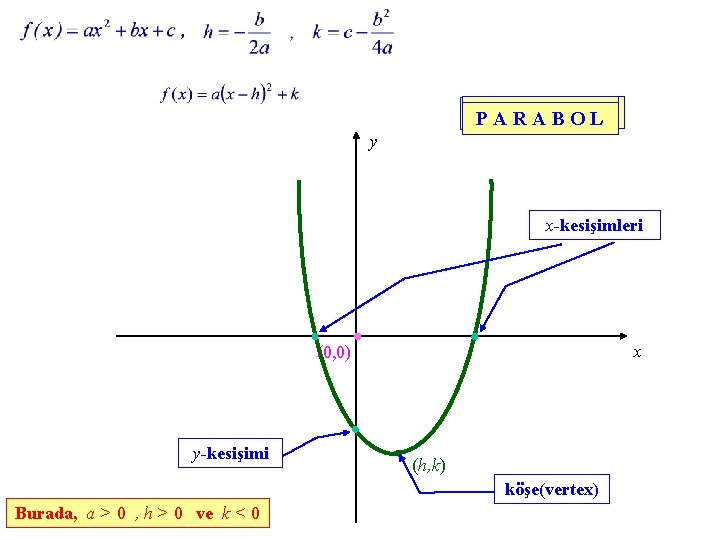
Bir Fonksiyonun Koordinat Kesişimleri(Intercepts). Bir fonksiyonun grafiğinin koordinat eksenlerini kestiği noktalara o fonksiyonun koordinat kesişimleri (intercepts) denir. Grafiğin x-eksenini kestiği noktalara fonksiyonun x-kesişimleri (x-intercepts), varsa y-eksenini kestiği noktaya da y-kesişimi (y-intercept) denir. x-kesişimleri : f(x) = 0 olan (x , 0) noktaları. y-kesişimi : Varsa, ( 0 , f(0)) noktası. y y= f(x) y-kesişimi x x-kesişimleri

Doğrusal Fonksiyonlar(Linear Functions). m ve b reel sayılar, m 0 olmak üzere f(x) = mx + b denklemi ile tanımlanan fonksiyona bir doğrusal fonksiyon (linear function) denir. Her doğrusal fonksiyonun tanım kümesi ve görüntü kümesi R dir. f(x) = x fonksiyonu bir doğrusal fonksiyondur: m=1 ve b=0. Her doğrusal fonksiyon, f(x) = x fonksiyonuna bazı elemanter transformasyonlar uygulanarak elde edilebilir. Bu nedenle, her doğrusal fonksiyonun grafiği bir doğrudur. y y y (0, b) (0, 0) x y=x (0, 0) x y = mx+ b

Dolayısıyla, bir doğrusal fonksiyonun grafiğini çizmek için iki farklı noktasını belirlemek yeterlidir. Özel olarak, koordinat kesişimlerinin belirlenmesi, grafik çizimi için yararlı olur. Örnek. f(x) = 2 x + 4 doğrusal fonksiyonunun grafiği: Koordinat kesişimleri, x-kesişimi : f(x) = 0 x = - 2 olduğundan, (-2 , 0). y-kesişimi : (0 , f(0)) = (0 , 4) y f(x) = 2 x + 4 (0 , 4) (-2 , 0) x (0, 0)

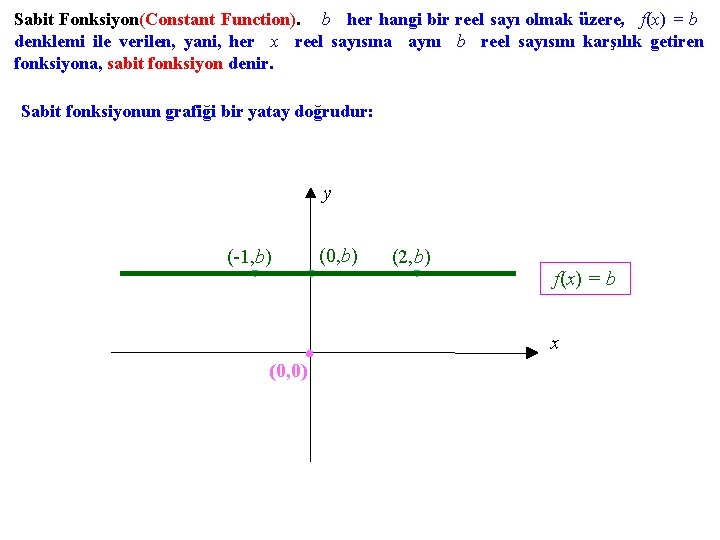
Sabit Fonksiyon(Constant Function). b her hangi bir reel sayı olmak üzere, f(x) = b denklemi ile verilen, yani, her x reel sayısına aynı b reel sayısını karşılık getiren fonksiyona, sabit fonksiyon denir. Sabit fonksiyonun grafiği bir yatay doğrudur: y (-1, b) (0, b) (2, b) f(x) = b x (0, 0)

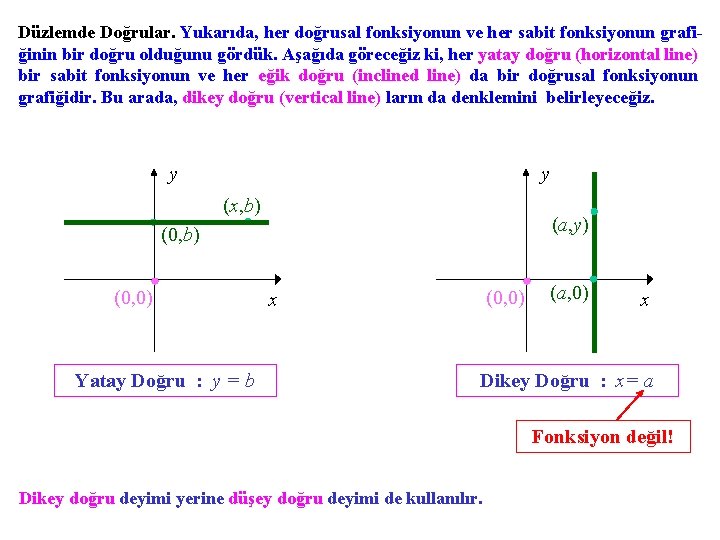
Düzlemde Doğrular. Yukarıda, her doğrusal fonksiyonun ve her sabit fonksiyonun grafiğinin bir doğru olduğunu gördük. Aşağıda göreceğiz ki, her yatay doğru (horizontal line) bir sabit fonksiyonun ve her eğik doğru (inclined line) da bir doğrusal fonksiyonun grafiğidir. Bu arada, dikey doğru (vertical line) ların da denklemini belirleyeceğiz. y y (x, b) (a, y) (0, b) (0, 0) Yatay Doğru : y = b (0, 0) x (a, 0) x Dikey Doğru : x= a Fonksiyon değil! Dikey doğru deyimi yerine düşey doğru deyimi de kullanılır.

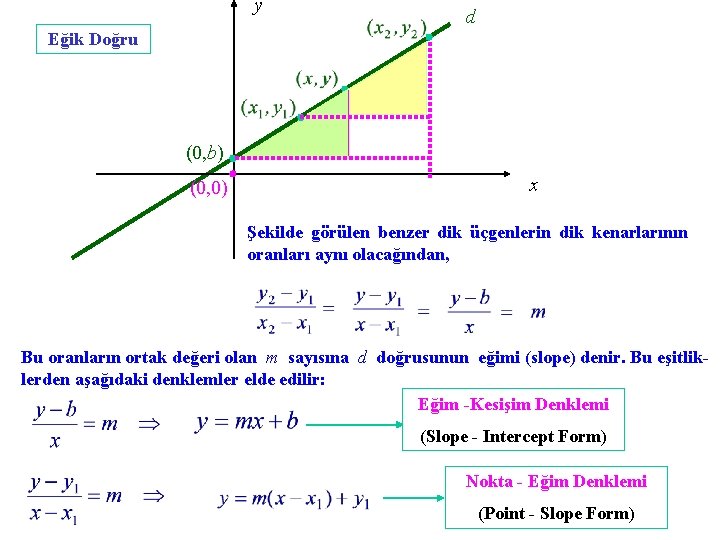
y d Eğik Doğru (0, b) (0, 0) x Şekilde görülen benzer dik üçgenlerin dik kenarlarının oranları aynı olacağından, Bu oranların ortak değeri olan m sayısına d doğrusunun eğimi (slope) denir. Bu eşitliklerden aşağıdaki denklemler elde edilir: Eğim -Kesişim Denklemi (Slope - Intercept Form) Nokta - Eğim Denklemi (Point - Slope Form)

Elde ettiğimiz denklemleri tekrar görelim: Eğim -Kesişim Denklemi (Slope - Intercept Form) Nokta - Eğim Denklemi (Point - Slope Form) Bir (x, y) noktasının d doğrusu üzerinde olması için gerek ve yeter koşul, o noktanın bu denklemlerden birini sağlamasıdır. Eğimi ve y - kesişimi bilinen bir doğrunun denklemi ile verilir. Eğimi ve bir noktası bilinen bir doğrunun denklemi ile verilir. İki noktası bilinen bir doğrunun denklemi de “nokta-eğim denklemi” olarak yazılabilir. Söz konusu iki nokta (x 1 , y 1 ) , ( x 2 , y 2 ) ise, doğrunun eğiminin olduğunu biliyoruz. Noktalardan biri ve eğim kullanılarak denklem elde edilir.

Örnekler. Şimdi doğru denklemlerine örnekler verelim. • Eğimi m = 3 ve y – kesişimi b = 4 olan doğrunun denklemi: Eğim – Kesişim Denklemi: • Eğimi m = 3 olan ve (-2 , 3) noktasından geçen doğrunun denklemi: Nokta – Eğim Denklemi: • (-2 , 3) ve (1 , 4) noktalarından geçen doğrunun denklemi : Bu doğrunun eğimi olacağından, (-2 , 3) noktası kullanılarak denklemi elde edilir.

Doğrusal Denklemler. olmak üzere, A , B ve C reel sayılar, A ve B den en az biri sıfırdan farklı Ax + By = C denklemine bir doğrusal denklem (linear equation) denir. A ve B ye bu denklemin katsayı (coefficient) ları, C ye de sağ taraf sabiti (right hand side constant) denir. x ve y sembollerine bu denklemin değişkenleri (variables) denir. Bundan önceki çalışmalarımız, bir doğrusal denklemin grafiğini belirlememize yardımcı olur: doğrusal fonksiyon, eğik doğru sabit fonksiyon, yatay doğru fonksiyon değil, düşey doğru

Elemanter Fonksiyonlar (Elementary Functions). Bu derste ve benzeri matematik derslerinde en çok karşılaşacağınız fonksiyonlar, elemanter fonksiyonlar olarak bilinen fonksiyonlardır. Aşağıda, elemanter fonksiyonları, grafikleriyle birlikte listeliyoruz: y Birim Fonksiyon: Her reel sayıya kendisini karşılık getiren fonksiyon. x f(x) = x y=x Tanım Kümesi : R Görüntü Kümesi : R Mutlak Değer Fonksiyonu: Her reel sayıya o sayının mutlak değerini karşılık getiren fonksiyon. y x Tanım Kümesi : R Görüntü Kümesi : [0, ) y = |x|

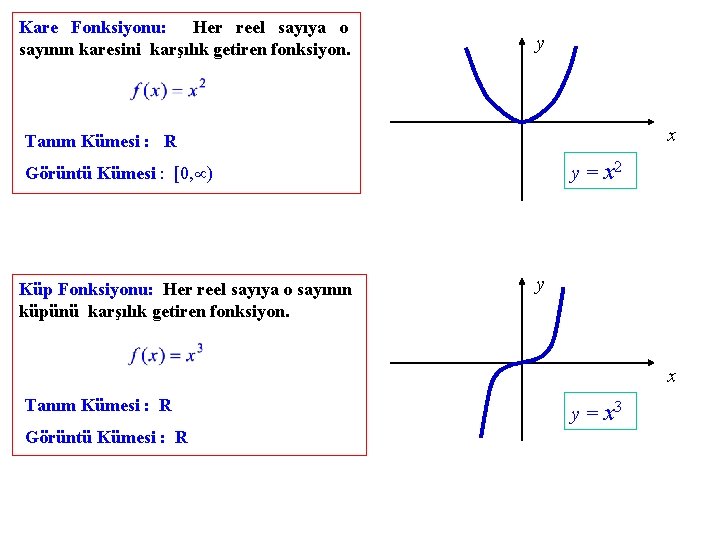
Kare Fonksiyonu: Her reel sayıya o sayının karesini karşılık getiren fonksiyon. y x Tanım Kümesi : R y = x 2 Görüntü Kümesi : [0, ) Küp Fonksiyonu: Her reel sayıya o sayının küpünü karşılık getiren fonksiyon. y x Tanım Kümesi : R Görüntü Kümesi : R y = x 3

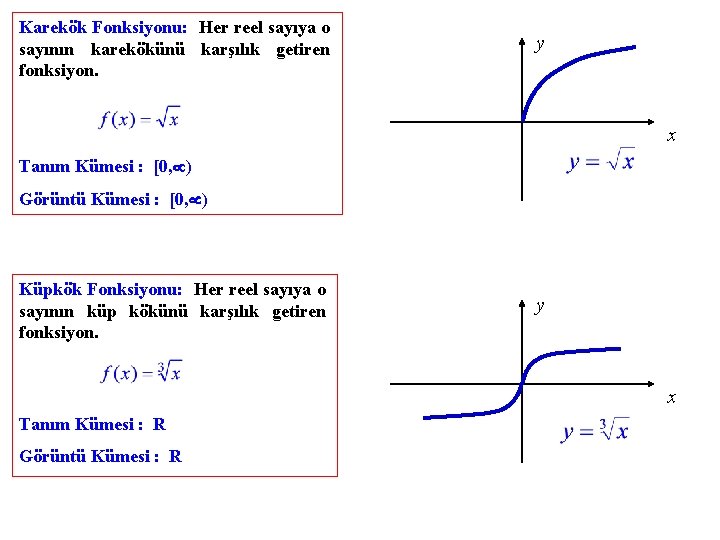
Karekök Fonksiyonu: Her reel sayıya o sayının karekökünü karşılık getiren fonksiyon. y x Tanım Kümesi : [0, ) Görüntü Kümesi : [0, ) Küpkök Fonksiyonu: Her reel sayıya o sayının küp kökünü karşılık getiren fonksiyon. y x Tanım Kümesi : R Görüntü Kümesi : R

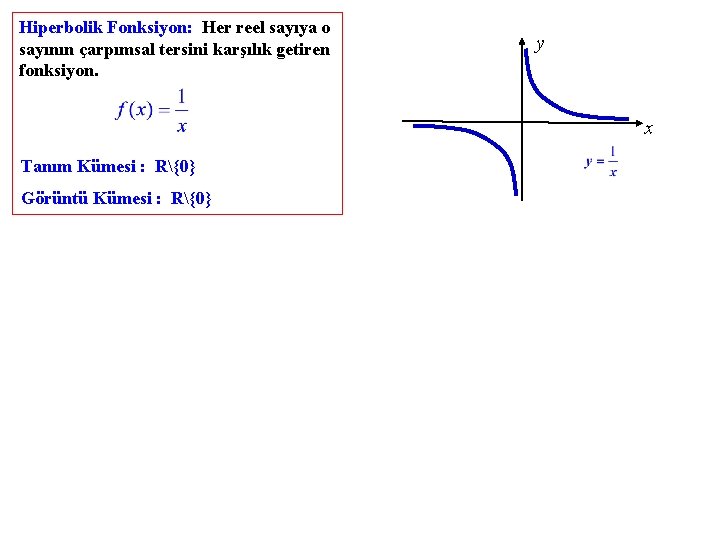
Hiperbolik Fonksiyon: Her reel sayıya o sayının çarpımsal tersini karşılık getiren fonksiyon. y x Tanım Kümesi : R{0} Görüntü Kümesi : R{0}

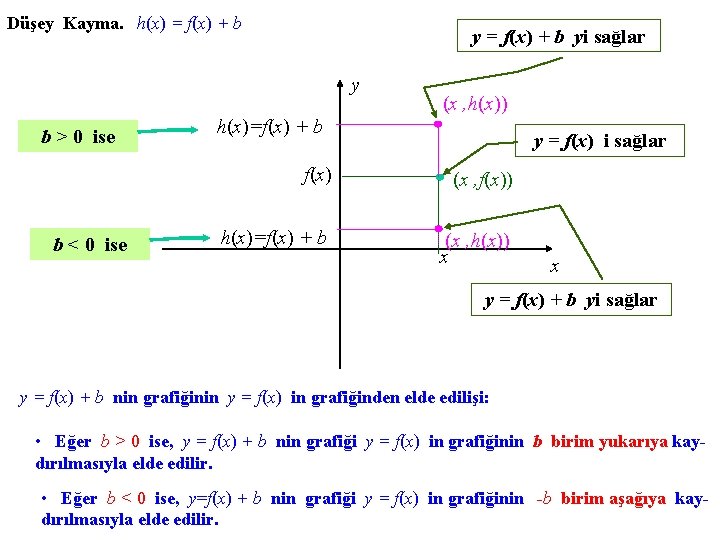
Düşey Kayma. h(x) = f(x) + b yi sağlar y b > 0 ise b < 0 ise (x , h(x)) h(x)=f(x) + b y = f(x) i sağlar f(x) (x , f(x)) h(x)=f(x) + b (x , h(x)) x x y = f(x) + b yi sağlar y = f(x) + b nin grafiğinin y = f(x) in grafiğinden elde edilişi: • Eğer b > 0 ise, y = f(x) + b nin grafiği y = f(x) in grafiğinin b birim yukarıya kaydırılmasıyla elde edilir. • Eğer b < 0 ise, y=f(x) + b nin grafiği y = f(x) in grafiğinin -b birim aşağıya kaydırılmasıyla elde edilir.

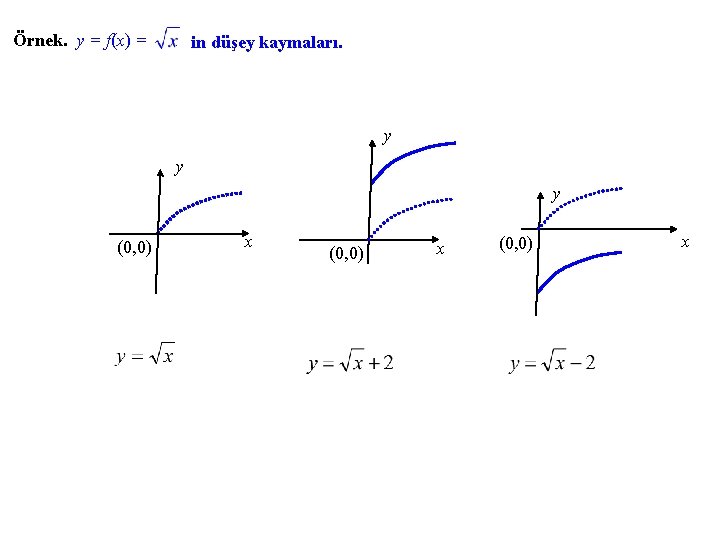
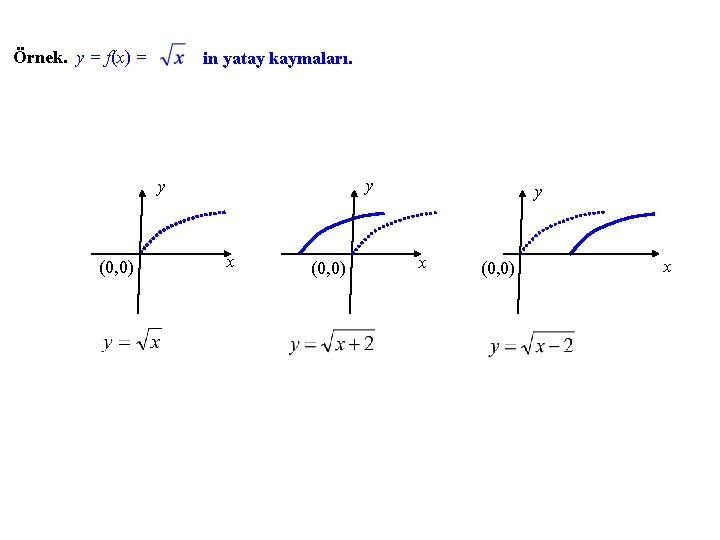
Örnek. y = f(x) = in düşey kaymaları. y y y (0, 0) x

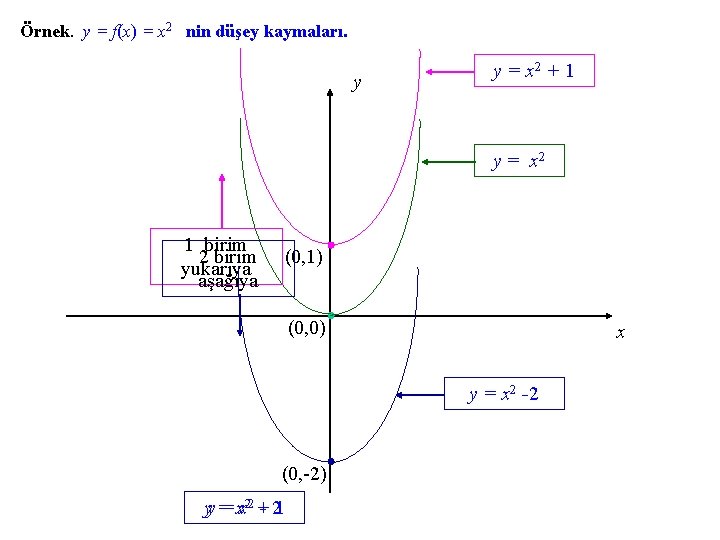
Örnek. y = f(x) = x 2 nin düşey kaymaları. y y = x 2 + 1 y = x 2 1 birim 2 birim yukarıya aşağıya (0, 1) (0, 0) x y = x 2 -2 (0, -2) yy = = xx 22 + - 21

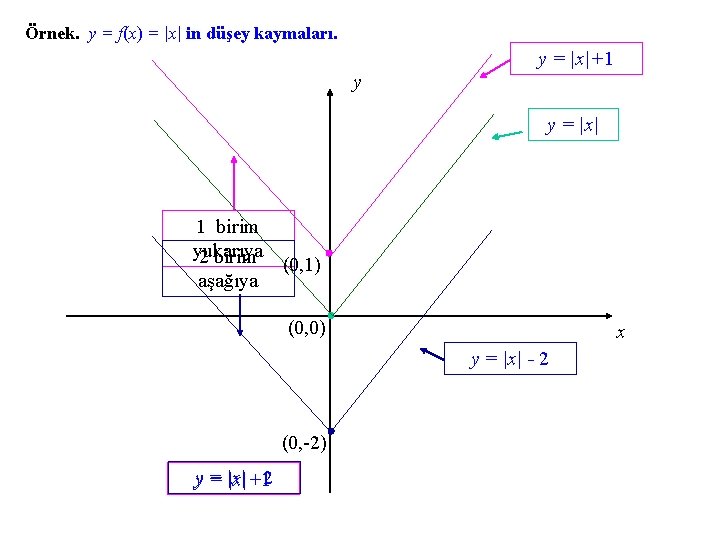
Örnek. y = f(x) = |x| in düşey kaymaları. y = |x|+1 y y = |x| 1 birim yukarıya 2 birim aşağıya (0, 1) (0, 0) x y = |x| - 2 (0, -2) y = |x| -2 |x|+1

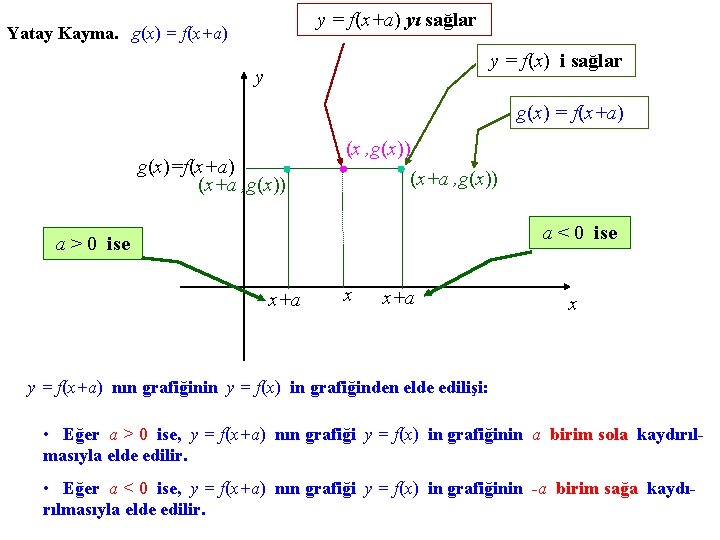
y = f(x+a) yı sağlar Yatay Kayma. g(x) = f(x+a) y = f(x) i sağlar y g(x) = f(x+a) g(x)=f(x+a) (x+a , g(x)) a < 0 ise a > 0 ise x+a x y = f(x+a) nın grafiğinin y = f(x) in grafiğinden elde edilişi: • Eğer a > 0 ise, y = f(x+a) nın grafiği y = f(x) in grafiğinin a birim sola kaydırılmasıyla elde edilir. • Eğer a < 0 ise, y = f(x+a) nın grafiği y = f(x) in grafiğinin -a birim sağa kaydırılmasıyla elde edilir.

Örnek. y = f(x) = in yatay kaymaları. y y (0, 0) x (0, 0) y x (0, 0) x

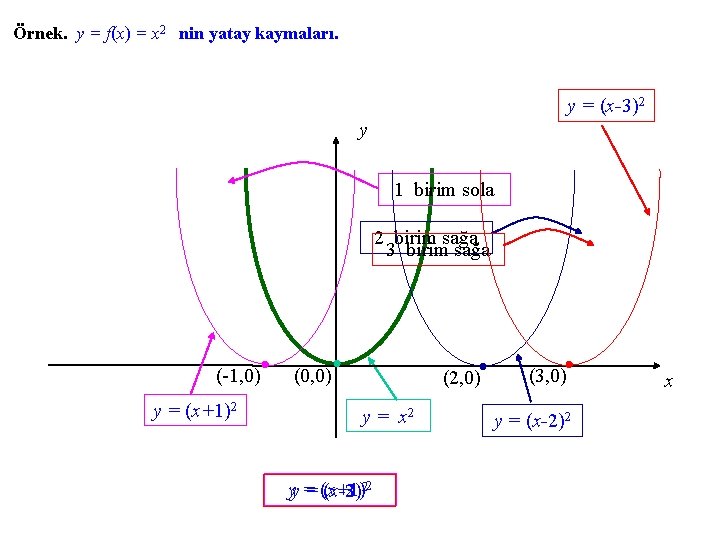
Örnek. y = f(x) = x 2 nin yatay kaymaları. y = (x-3)2 y 1 birim sola 2 birim sağa 3 birim sağa (-1, 0) y = (x+1)2 (0, 0) (2, 0) y = x 2 yy = = (x+1) (x-2)22 (x-3) (3, 0) y = (x-2)2 x

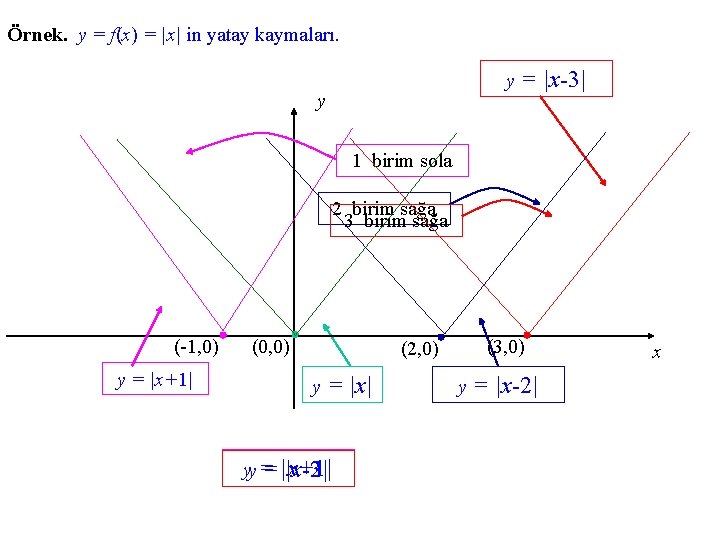
Örnek. y = f(x) = |x| in yatay kaymaları. y y = |x-3| 1 birim sola 2 birim sağa 3 birim sağa (-1, 0) y = |x+1| (0, 0) (3, 0) (2, 0) y = |x| yy = = |x+1| |x-2| |x-3| y = |x-2| x

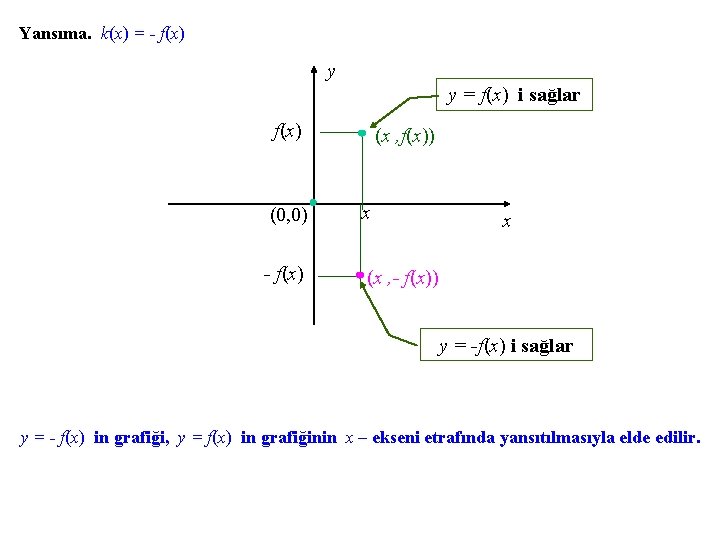
Yansıma. k(x) = - f(x) y y = f(x) i sağlar f(x) (x , f(x)) (0, 0) x - f(x) (x , - f(x)) x y = -f(x) i sağlar y = - f(x) in grafiği, y = f(x) in grafiğinin x – ekseni etrafında yansıtılmasıyla elde edilir.

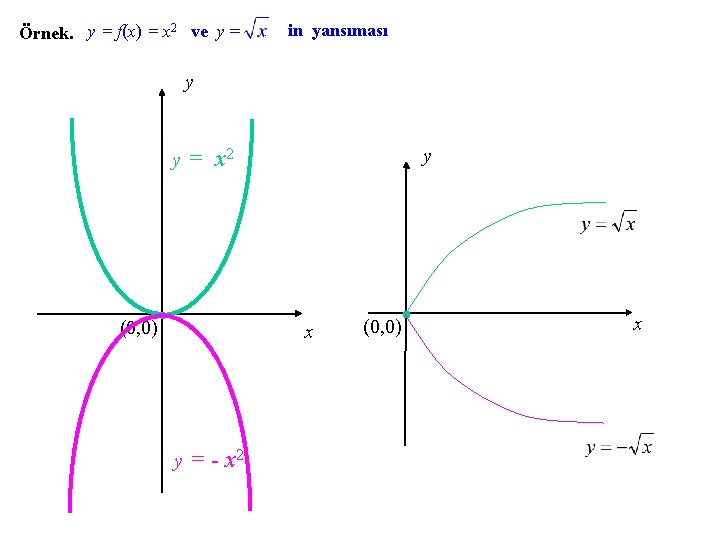
Örnek. y = f(x) = x 2 ve y = in yansıması y y y = x 2 (0, 0) x y = - x 2 (0, 0) x

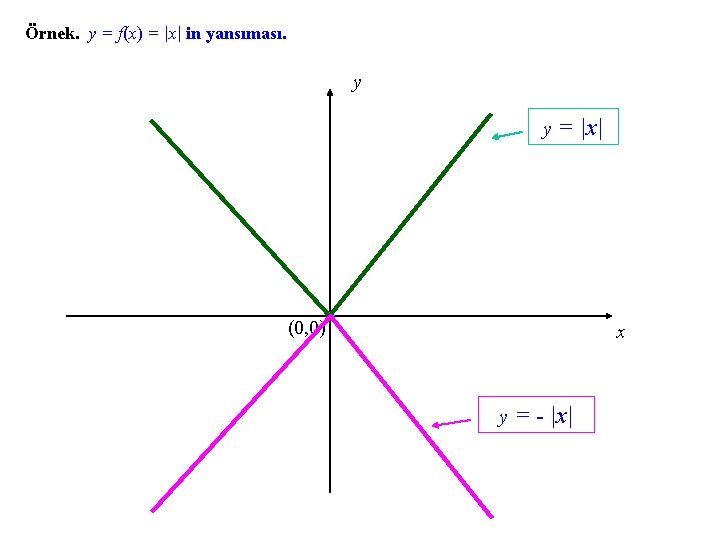
Örnek. y = f(x) = |x| in yansıması. y y = |x| (0, 0) x y = - |x|

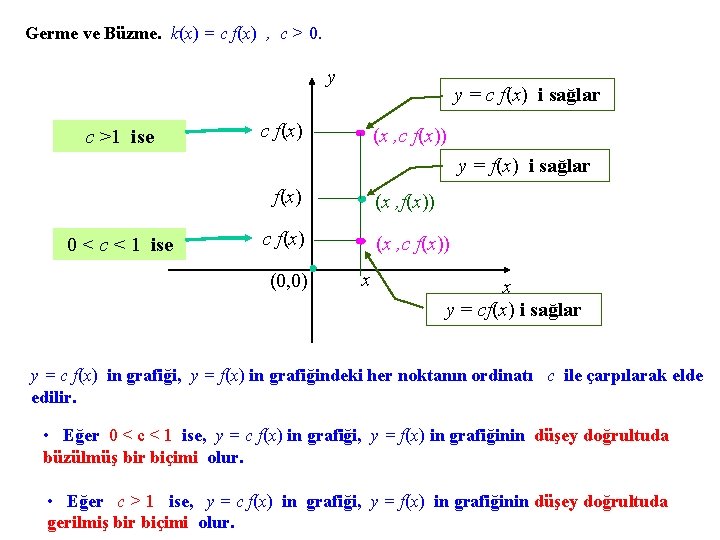
Germe ve Büzme. k(x) = c f(x) , c > 0. y c >1 ise y = c f(x) i sağlar c f(x) (x , c f(x)) y = f(x) i sağlar f(x) 0 < c < 1 ise (x , f(x)) c f(x) (0, 0) (x , c f(x)) x x y = cf(x) i sağlar y = c f(x) in grafiği, y = f(x) in grafiğindeki her noktanın ordinatı c ile çarpılarak elde edilir. • Eğer 0 < c < 1 ise, y = c f(x) in grafiği, y = f(x) in grafiğinin düşey doğrultuda büzülmüş bir biçimi olur. • Eğer c > 1 ise, y = c f(x) in grafiği, y = f(x) in grafiğinin düşey doğrultuda gerilmiş bir biçimi olur.

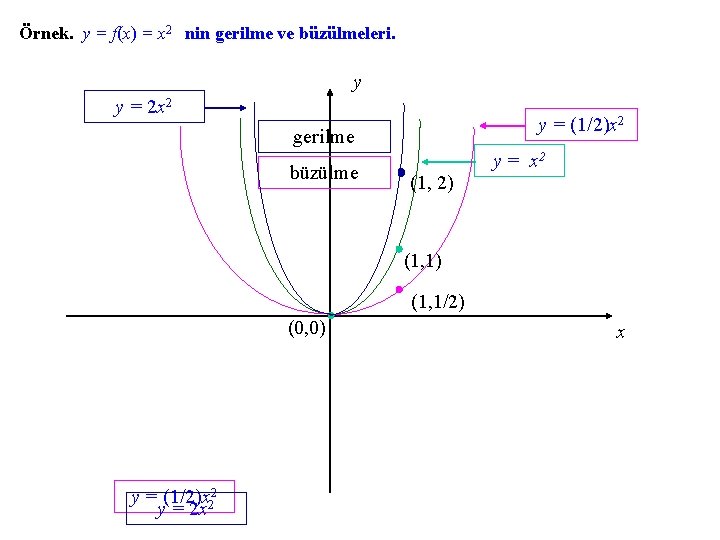
Örnek. y = f(x) = x 2 nin gerilme ve büzülmeleri. y y = 2 x 2 y = (1/2)x 2 gerilme büzülme (1, 2) y = x 2 (1, 1) (1, 1/2) (0, 0) y = (1/2)x 22 y = 2 x x

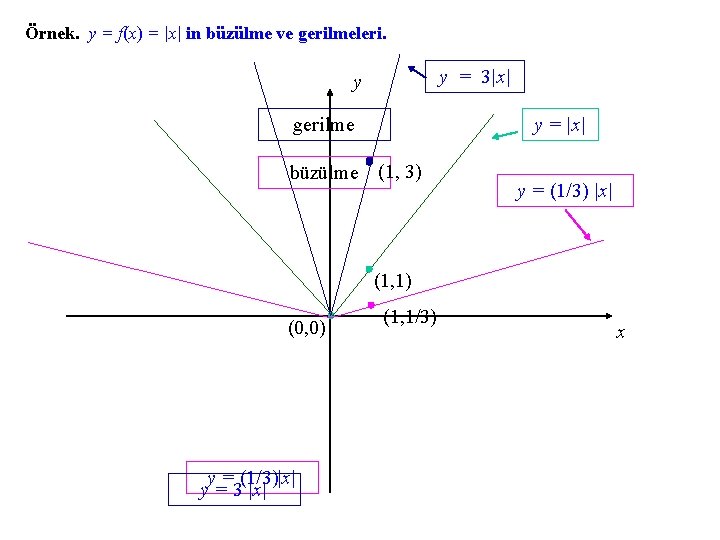
Örnek. y = f(x) = |x| in büzülme ve gerilmeleri. y = 3|x| y gerilme büzülme y = |x| (1, 3) y = (1/3) |x| (1, 1) (0, 0) y = (1/3)|x| y = 3 |x| (1, 1/3) x

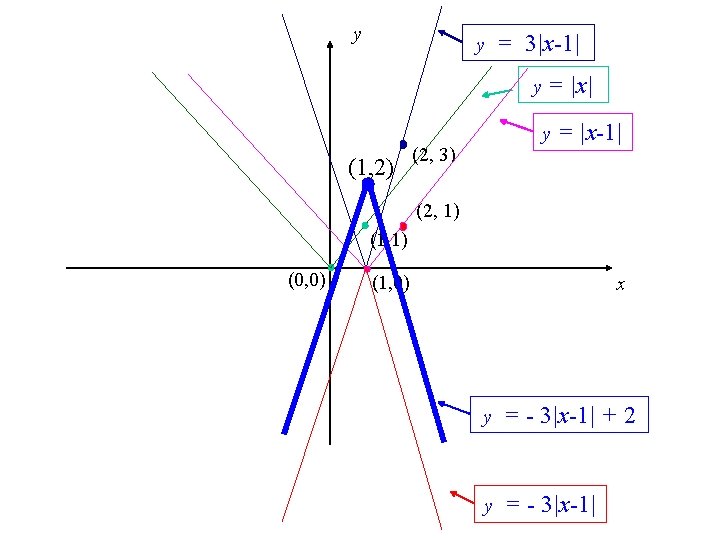
Kayma, Yansıma, Gerilme ve Büzülmelerin Art Arda Uygulanması. Pratikte karşılaştığımız fonksiyonlardan pek çoğu, elemanter fonksiyonlara daha önce gördüğümüz transformasyonların art arda uygulanmasıyla elde edilir. Örnek. y = -3 |x - 1| + 2 nin grafiği, y = |x| in grafiğinden elde edilebilir. y = |x| y = |x - 1| y = 3|x - 1| y = -(3|x - 1| ) + 2

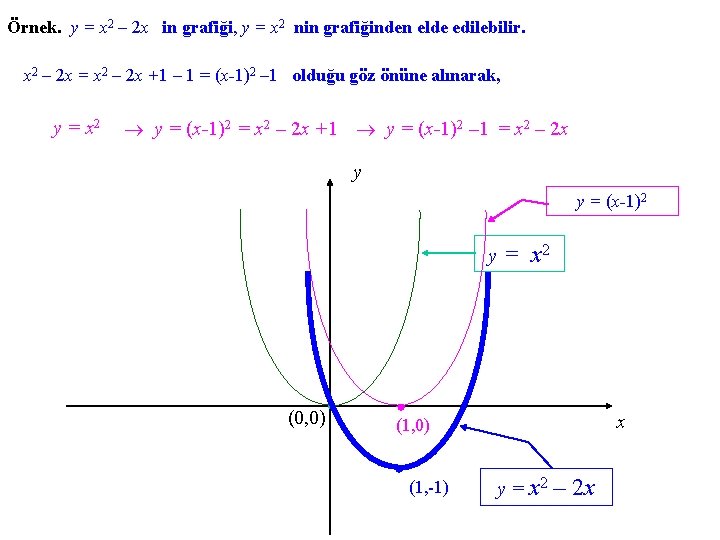
Örnek. y = x 2 – 2 x in grafiği, y = x 2 nin grafiğinden elde edilebilir. x 2 – 2 x = x 2 – 2 x +1 – 1 = (x-1)2 – 1 olduğu göz önüne alınarak, y = x 2 y = (x-1)2 = x 2 – 2 x +1 y = (x-1)2 – 1 = x 2 – 2 x y y = (x-1)2 y (0, 0) = x 2 x (1, 0) (1, -1) y = x 2 – 2 x

Aşağıdaki denklemlerle tanımlanan g, h ve k fonksiyonlarını ele alalım: Bu fonksiyonlar fonksiyonu cinsinden ifade edilebilir: g(x) = f(x-2) , h(x) = f(x) – 1 , k(x) = 3 f(x). Aşağıda göreceğimiz üzere, g, h ve k fonksiyonlarının grafikleri de f fonksiyonunun grafiği cinsinden elde edilebilir. g, h ve k fonksiyonlarının f fonksiyonu cinsinden tanımı en genel biçimiyle şöyle verilebilir: a, b ve c reel sayılar olmak üzere g(x) = f(x+a) Yatay kayma , h(x) = f(x) + b , Düşey kayma k(x) = c f(x). c = -1 : Yansıma c >1 : Germe 0 < c <1 : Büzme

Karesel Fonksiyonlar. a , b ve c reel sayılar, a 0 olmak üzere, f(x) = ax 2 + bx + c denklemi ile verilen fonksiyona bir karesel fonksiyon (quadratic function) denir. Bazı kitaplarda karesel sözcüğü yerine kuadratik sözcüğü de kullanılır. Kareye tamamlama denilen işlemle ve son ifadede yazılarak her karesel fonksiyon biçimine dönüştürülebilir.

Varılan sonucu özetleyelim: Son ifadeden görüyoruz ki, her karesel fonksiyon y = x 2 kare fonksiyonuna elemanter transformasyonlar uygulanarak elde edilebilir. Dolayısıyla, karesel fonksiyonun grafiği de y = x 2 nin grafiğinin kaydırılması, x-ekseni etrafında yansıtılması veya büzülüp gerilmesiyle elde edilir. Karesel fonksiyonun grafiği parabol (parabola) olarak adlandırılır. Sağa veya sola kayma Germe, büzme veya yansıma Yukarı veya aşağı kayma

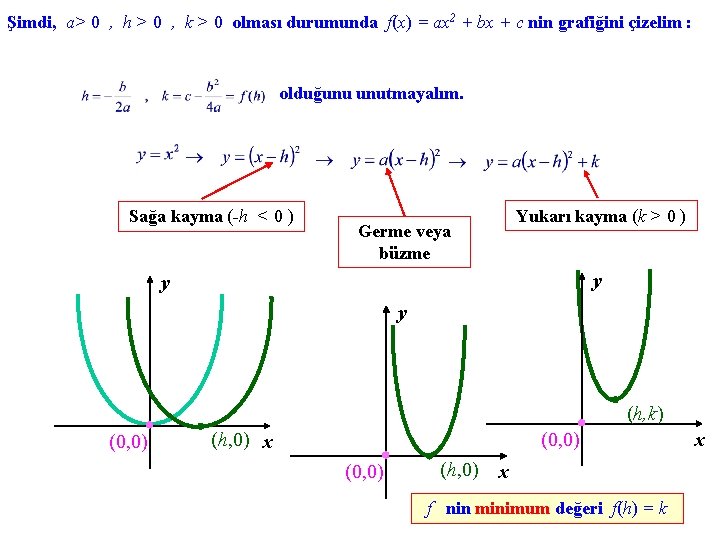
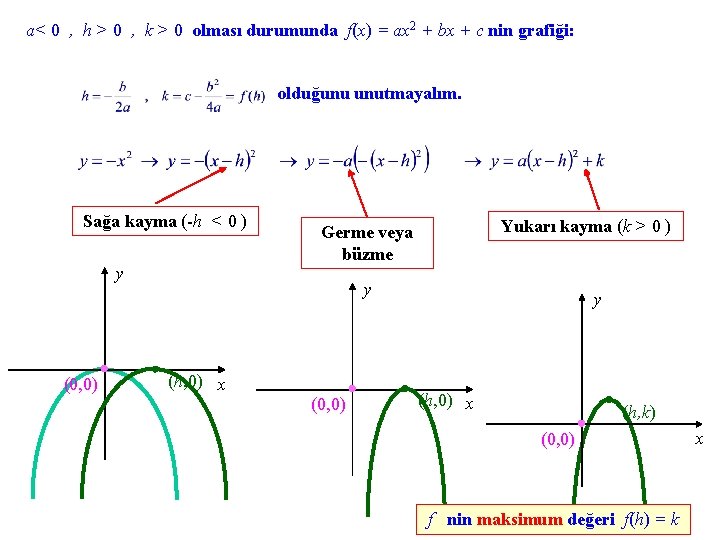
Şimdi, a> 0 , h > 0 , k > 0 olması durumunda f(x) = ax 2 + bx + c nin grafiğini çizelim : olduğunu unutmayalım. Sağa kayma (-h < 0 ) Yukarı kayma (k > 0 ) Germe veya büzme y y y (h, k) (0, 0) (h, 0) x f nin minimum değeri f(h) = k x

a< 0 , h > 0 , k > 0 olması durumunda f(x) = ax 2 + bx + c nin grafiği: olduğunu unutmayalım. Sağa kayma (-h < 0 ) y (0, 0) Yukarı kayma (k > 0 ) Germe veya büzme y (h, 0) x (0, 0) y (h, 0) x (h, k) (0, 0) f nin maksimum değeri f(h) = k x

y = a(x-h)2 ifadesinde (x-h)2 nin alabileceği en küçük değer x = h için sıfır değeri olduğundan, f(x)= a(x-h)2 + k karesel fonksiyonu için f(h) = k değeri, a > 0 olması durumunda minimum, a < 0 olması durumunda maksimum değerdir. f(x)= a(x-h)2 + k karesel fonksiyonunun a > 0 olması durumunda maksimum değeri, a < 0 olması durumunda da minimum değeri yoktur. (h, k) noktasına karesel fonksiyonunun (veya onun grafiği olan parabolün) köşe veya tepe noktası denir. a > 0 olması durumunda, köşe noktası parabolün en alt, yani dip noktasıdır ve parabol yukarıya doğru açılır ; a < 0 olması durumunda, köşe noktası parabolün en üst, yani tepe noktasıdır ve parabol aşağıya doğru açılır. Bir karesel fonksiyonun grafiği, koordinat kesişimleri ve köşe noktası belirlenip yukarıdaki bilgilerden yararlanılarak çizilir.

P PPA AAR RRA AAB BBO OOL LL y x-kesişimleri x (0, 0) y-kesişimi (h, k) köşe(vertex) Burada, a > 0 , h > 0 ve k < 0

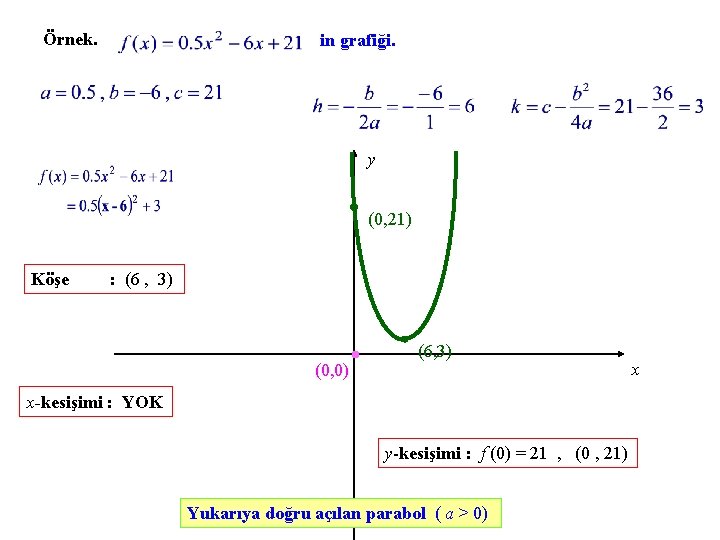
Örnek. in grafiği. y (0, 21) Köşe : (6 , 3) (0, 0) (6, 3) x-kesişimi : YOK y-kesişimi : f (0) = 21 , (0 , 21) Yukarıya doğru açılan parabol ( a > 0) x

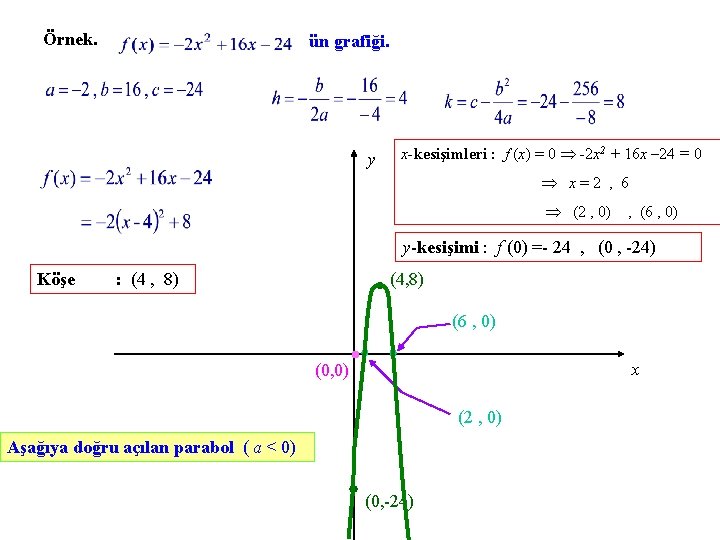
Örnek. ün grafiği. y x-kesişimleri : f (x) = 0 -2 x 2 + 16 x – 24 = 0 x=2 , 6 (2 , 0) , (6 , 0) y-kesişimi : f (0) =- 24 , (0 , -24) Köşe : (4 , 8) (4, 8) (6 , 0) x (0, 0) (2 , 0) Aşağıya doğru açılan parabol ( a < 0) (0, -24)

Karesel fonksiyonlarla ilgili bilgileri özetleyelim: • f nin grafiği, köşe noktası (h , k) olan paraboldür. f nin y-kesişimi (0 , c ) noktasıdır; x-kesişimleri ax 2 + bx + c = 0 denklemi çözülerek belirlenir. • Eğer a > 0 ise, parabol yukarıya doğru açılır ve f nin minimum değeri f(h) =k dir. Fonksiyonun görüntü kümesi, [k, ∞) aralığıdır. • Eğer a < 0 ise, parabol aşağıya doğru açılır ve f nin maksium değeri f(h) =k dir. Fonksiyonun görüntü kümesi, (- ∞, k] aralığıdır.

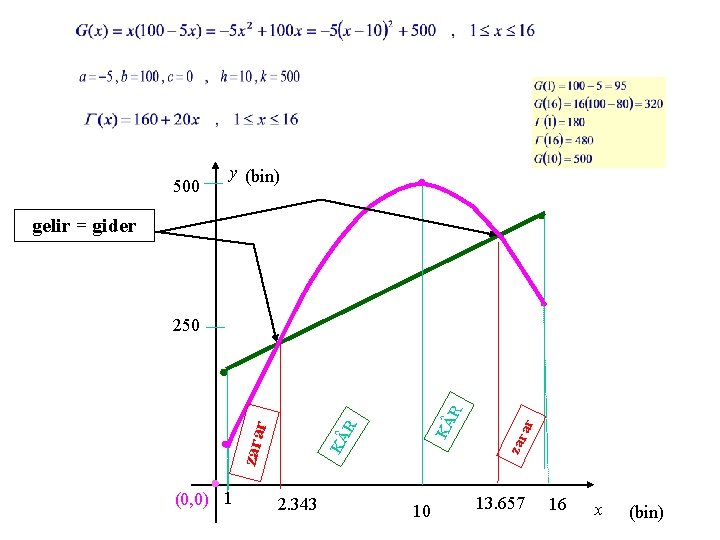
Uygulama. Bir firmanın gelir ve gider fonksiyonları, x bin adet ürün için bin TL olarak veriliyor. G ve nın grafiklerini aynı koordinat düzleminde çizerek aşağıdaki soruları yanıtlayınız: a) Gelir ve giderin eşit olduğu x sayılarını bulunuz. b) Kâr edilen ve zarar edilen bölgeleri ve en büyük kârı belirleyiniz. Çözüm. Gelir fonksiyonu, biçiminde ifade edilebilen karesel fonksiyondur. Gider fonksiyonu da bir doğrusal fonksiyondur ve grafikler şöyledir:

500 y (bin) gelir = gider (0, 0) 1 2. 343 10 ar zar K K R zarar R 250 13. 657 16 x (bin)

Kâr fonksiyonuna bakalım: Maksimum kâr : 160 000 TL. (bin TL).