F O N K S YO N FONKSYON






























































![ÖRNEK : 70 [ ( f o g )-1 o f ] ( x ÖRNEK : 70 [ ( f o g )-1 o f ] ( x](https://slidetodoc.com/presentation_image_h/352e99d84891d79d1a90da5165505466/image-96.jpg)


























































- Slides: 157

F O N K S İ YO N

FONKSİYON KONUSU SORU DAĞILIMI 1997 1998 2 3 1999 ( iptal ) 1 1 2000 2001 2002 2003 2004 1 - - 1 - Fonksiyon konusundaki soru tipleri genel olarak şu şekilde gruplandırılabilir. Fonksiyon tanımı Fonksiyon Çeşitleri Cinsinden - Türünden Grafik

1997 -2004 ÖSS’lerinde , fonksiyon konusundan toplam 9 sorulmuştur. Bu soruların soru tiplerine göre dağılımı 3 tane fonksiyon tanımından 3 tane fonksiyon çeşitlerinden 3 tane grafik

Fonksiyon konusu oldukça geniş ve kapsamlı bir konudur. Konunun iyi anlaşılabilmesi için soru tiplerini gruplandırarak çalışmak ve özellikle çözümlü örnekleri tekrar çözmek gerekmektedir. Bu sayede fonksiyon konusunun mantığı anlaşılabilecek ve çıkacak olan soru çözülebilecektir. Konuyu çalışırken önceliği değer – tanım kümesi ilişkisi , ters - bileşke fonksiyon ve grafik sorularına vermek gerekir. Konu kapsamlı olduğu içinde daha fazla zaman ayrılması iyi olacaktır.

ÖRNEK : 1 A B İPLİK FABRİKA KUMAŞ FABRİKANIN FONKSİYONU İPLİKTEN KUMAŞ ÜRETMESİDİR.

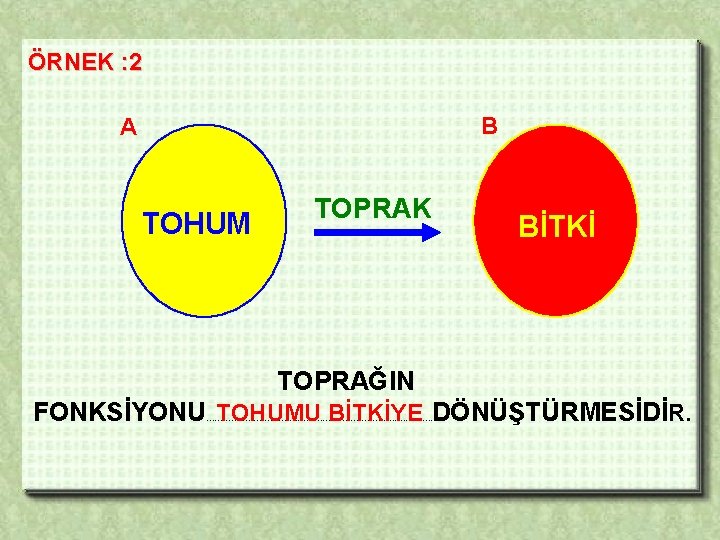
ÖRNEK : 2 B A TOHUM TOPRAK BİTKİ TOPRAĞIN FONKSİYONU TOHUMU BİTKİYE DÖNÜŞTÜRMESİDİR. . . . . .

A ve B boş olmayan iki küme olsun. AXB nin her alt kümesine A da B ye bir bağıntı dendiğini biliyorsunuz. Şimdi , A dan B ye tanımlanan bağıntılarından bazılarının aşağıda değineceğimiz şartları doğrulamasını isteyeceğiz ve bu bağıntılara fonksiyon diyeceğiz. TANIM: A ve B boş olmayan herhangi iki küme olsun. A’nın her elemanını B’ nin bir ve yalnız bir elemanına eşleyen f bağıntısına A dan B ye fonksiyon denir. f Bu durum f : A B veya A B biçiminde gösterilir.

TANIM: A’ dan B’ ye f fonksiyonu A’ nın bir x elemanını B ’ nin bir y elemanına eşlesin , y ’ye x ’ in f altında görüntüsü denir. Bu durum ; ff f: x y , y =f(x) , (x, y) f İfadelerinden biri ile gösterilir. A kümesine f fonksiyonun tanım kümesi , B kümesine bu fonksiyonun değer kümesi ve A ’ nın elemanlarının B kümesindeki görüntülerinin oluşturduğu kümeye görüntü kümesi denir. Görüntü kümesi f(A) ile gösterilir.

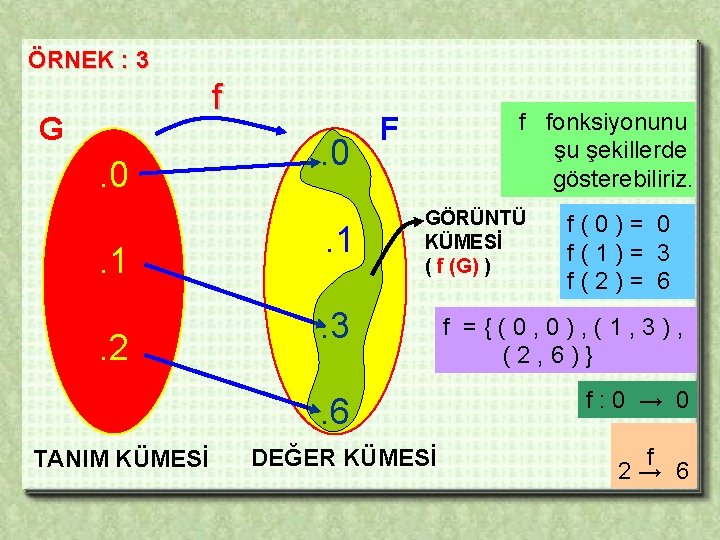
ÖRNEK : 3 f G . 0. 1. 2 TANIM KÜMESİ . 0. 1 f fonksiyonunu şu şekillerde gösterebiliriz. F GÖRÜNTÜ KÜMESİ ( f (G) ) f(0)= 0 f(1)= 3 f(2)= 6 . 3 f ={(0, 0), (1, 3), (2, 6)} . 6 f: 0 → 0 DEĞER KÜMESİ f 2→ 6

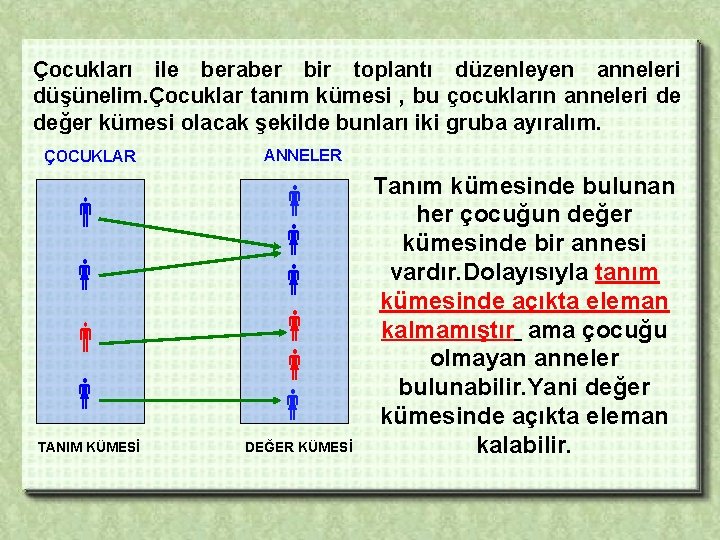
ÖRNEK : 4 f G . 0 . 1. 2. 3. 5 . 1. 2. 3 F Yanda şeması verilen f fonksiyonunun : a) Tanım kümesini yazınız. b) Değer kümesini yazınız. c) Görüntü kümesini yazınız. ÇÖZÜM: Tanım Kümesi , Değer Kümesi Görüntü Kümesi , D={0, 1, 2, 3, 5 } , f(G)={ 1, 2, 3, 5 } T = { 0 , 1 , 2 , 3 }

FONKSİYONUN ÖZELLİKLERİ 1 - Tanım kümesinde açıkta eleman kalmaz, değer kümesinde açıkta eleman kalabilir. 2 - Tanım kümesinde bir eleman değer kümesindeki birden fazla elemanla eşlenemez. 3 - Tanım kümesindeki birden fazla eleman değer kümesindeki bir elemanla eşlenebilir. Bu özelliklerin daha iyi aklımızda kalması için şu örneği verebiliriz

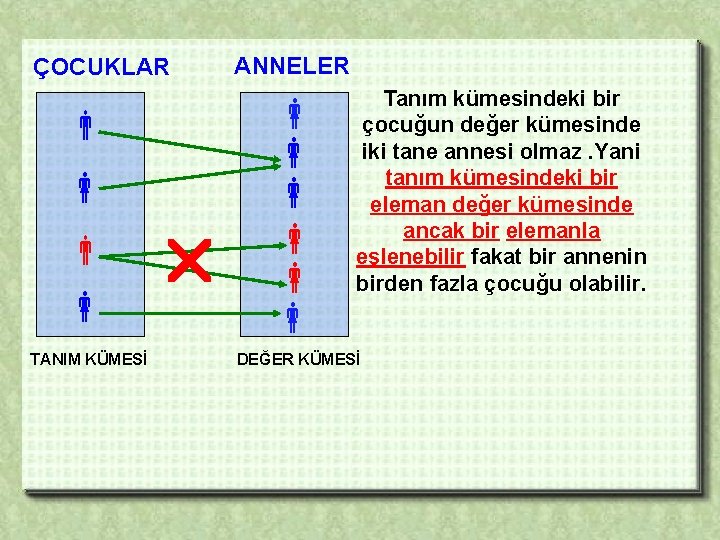
Çocukları ile beraber bir toplantı düzenleyen anneleri düşünelim. Çocuklar tanım kümesi , bu çocukların anneleri de değer kümesi olacak şekilde bunları iki gruba ayıralım. ÇOCUKLAR TANIM KÜMESİ ANNELER DEĞER KÜMESİ Tanım kümesinde bulunan her çocuğun değer kümesinde bir annesi vardır. Dolayısıyla tanım kümesinde açıkta eleman kalmamıştır ama çocuğu olmayan anneler bulunabilir. Yani değer kümesinde açıkta eleman kalabilir.

ÇOCUKLAR TANIM KÜMESİ ANNELER Tanım kümesindeki bir çocuğun değer kümesinde iki tane annesi olmaz. Yani tanım kümesindeki bir eleman değer kümesinde ancak bir elemanla eşlenebilir fakat bir annenin birden fazla çocuğu olabilir. DEĞER KÜMESİ

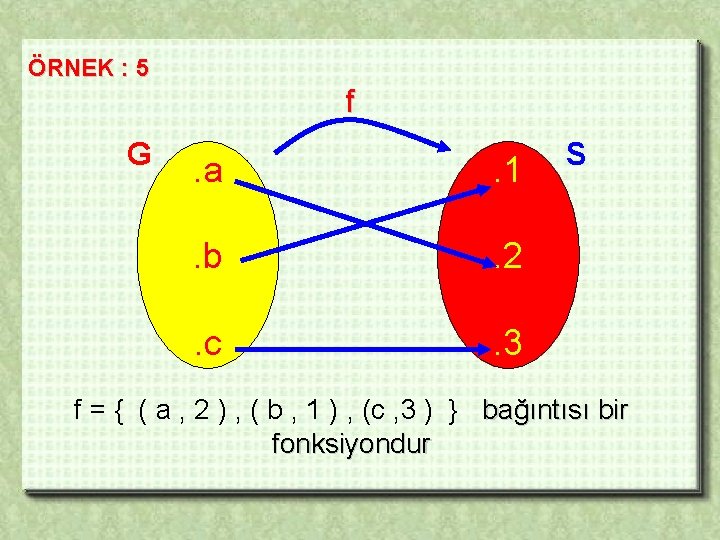
ÖRNEK : 5 f G . a . 1 . b . 2 . c . 3 S f = { ( a , 2 ) , ( b , 1 ) , (c , 3 ) } bağıntısı bir fonksiyondur

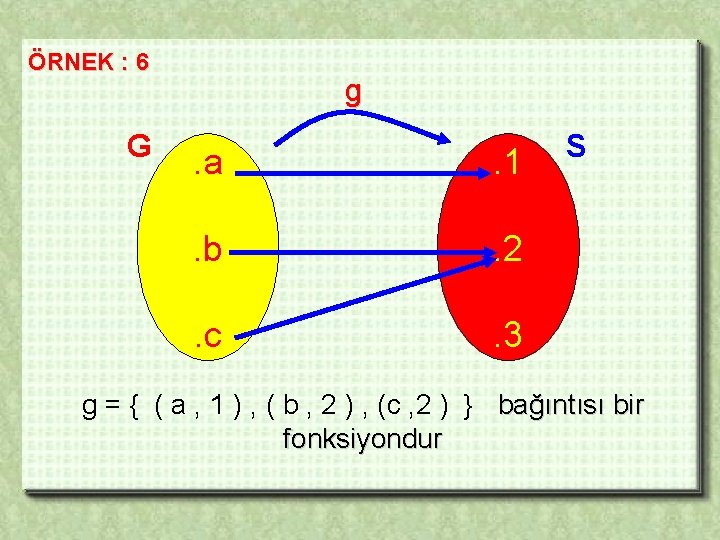
ÖRNEK : 6 G g . a . 1 . b . 2 . c . 3 S g = { ( a , 1 ) , ( b , 2 ) , (c , 2 ) } bağıntısı bir fonksiyondur

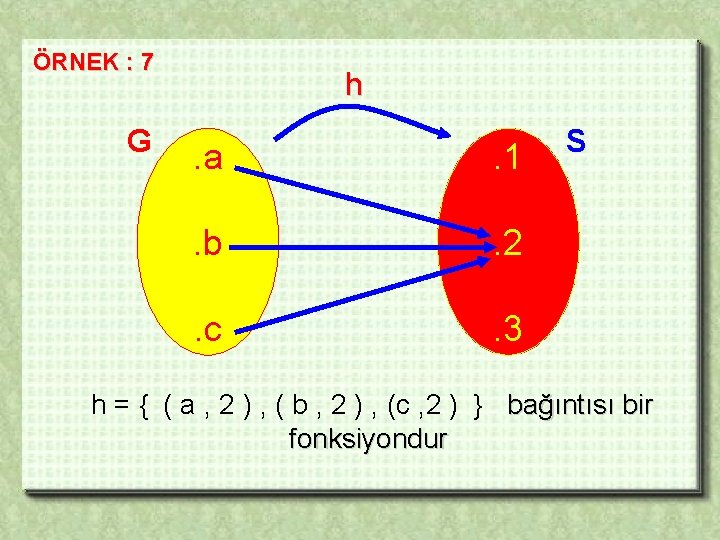
ÖRNEK : 7 G h . a . 1 . b . 2 . c . 3 S h = { ( a , 2 ) , ( b , 2 ) , (c , 2 ) } bağıntısı bir fonksiyondur

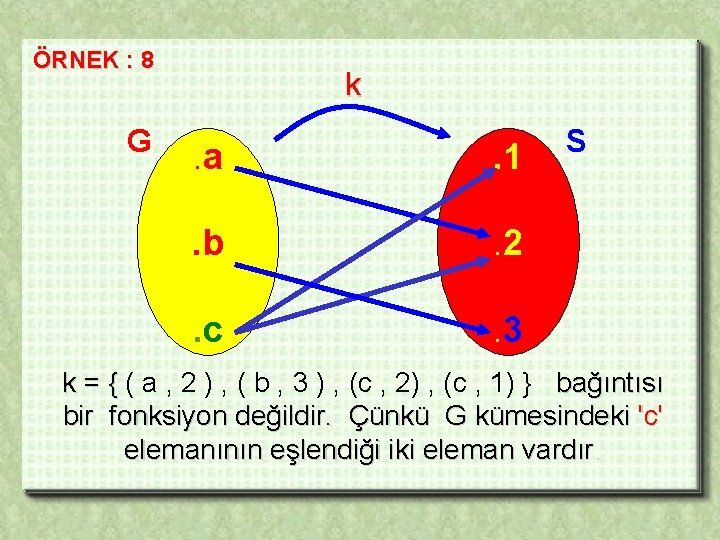
ÖRNEK : 8 G k . a . 1 . b . 2 . c . 3 S k = { ( a , 2 ) , ( b , 3 ) , (c , 2) , (c , 1) } bağıntısı bir fonksiyon değildir. Çünkü G kümesindeki 'c' elemanının eşlendiği iki eleman vardır.

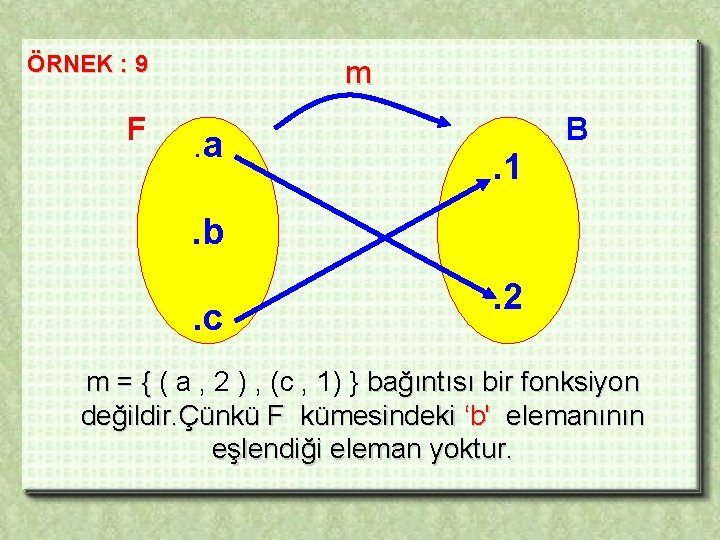
ÖRNEK : 9 F m . a . 1 B . b. c . 2 m = { ( a , 2 ) , (c , 1) } bağıntısı bir fonksiyon değildir. Çünkü F kümesindeki ‘b' elemanının eşlendiği eleman yoktur.

UYARI: Her fonksiyon bir bağıntıdır fakat her bağıntı bir fonksiyon değildir. Fonksiyon tanımını gerçekleyen özel bağıntılar fonksiyon olur.

Bir ineğin delidana hastası olduğunu nasıl anlarsınız? Eğer ineğinizin sesi şöyleyse: (Çift tıklayın) ızgaranızın ateşini yakın. . . Eğer ineğinizin sesi şöyleyse: (Çift tıklayın) balık yemeniz ruh sağlığınız açısından daha iyi olur. . .

ÖRNEK : 10 A = { a , b , c } kümesinden B = { 5 , 6 , 7 , 8 } kümesine tanımlanan aşağıdakilerden hangisi bir fonksiyon belirtir? a ) β 1= { ( a , 5 ) , ( b , 5 ) , (c , 5 ) } b ) β 2= { ( a , 5 ) , ( a , 6 ) , (a , 7 ) , ( b , 5 ) , ( b , 7 ) } c ) β 3= { ( a , 8 ) , ( a , 7 ) , (b , 8 ) , ( b , 5 ) } d ) β 4= { ( a , 5 ) , ( b , 6 ) , ( b , 7 ) , ( c , 8 ) } e ) β 5= { ( c , 5 ) , ( a , 6 ) , (c , 7 ) , ( c , 8 ) } ÇÖZÜM Bir bağıntının fonksiyon olabilmesi için tanım kümesindeki ( A ’da ki ) her elemanın yalnız bir tane görüntüsü olmalıdır. β 1 bu şartı sağladığı için fonksiyondur.

UYARI: s( A ) =n ve s( B ) = m olmak üzere A dan B ye tanımlanabilen fonksiyon sayısı mn dir. ÖRNEK: 11 s(A) = 2 ve A’dan B’ye 144 fonksiyon tanımlanabildiğine göre s(B)=? ÇÖZÜM: s( A ) =2 s( B )= m olsun A’dan B’ye tanımlanabilen fonksiyon sayısı n 2 dir. Buna göre m 2 = 144 m = 12 = s( B )

UYARI: s( A ) =n ve s( B ) = m olmak üzere A dan B ye fonksiyon olmayan bağıntı sayısı ; 2 n. m - mn dir. ÖRNEK: 12 s( A ) = 2 ve s( B ) = 3 ise A dan B ye fonksiyon olmayan bağıntı sayısı kaçtır? ÇÖZÜM: A’ dan B’ ye sayısı ; tanımlanabilen fonksiyon olmayan bağıntı 22. 3 - 32 = 26 - 9 = 64 - 9 = 55

ÖRNEK : 13 A = { - 2 , - 1 , 0 , 1 , 2 } , B = { - 6 , - 4 , - 3 , 0 , 1 , 3 , 6 } kümeleri için f : A → B , f ( x ) = 3 x bağıntısı verilsin: a) f bağıntısını şema ile gösterelim. Fonksiyon olup olamadığını belirtelim. b) f : A →B ye bir fonksiyon ise f(A) kümesini bulunuz. c) f fonksiyonunu ikililer halinde yazınız. ÇÖZÜM: x = - 2 için f ( - 2 ) = 3. ( -2 ) = - 6 ( -2 ' nin görüntüsü -6 dır ) x = - 1 için f ( - 1 ) = 3. ( -1 ) = - 3 ( -1 ' in görüntüsü -3 dür ) x = 0 için f ( 0 ) = 3. ( 0 ) = 0 ( 0 ' ın görüntüsü 0 dır ) x = 1 için f ( 1 ) = 3 ( 1 ' in görüntüsü 3 dür ) x = 2 için f ( 2 ) = 3. ( 2 ) = 6 ( 2 ' nin görüntüsü 6 dır )

x = - 2 için f ( - 2 ) = 3. ( -2 ) = - 6 ( -2 ' nin görüntüsü -6 dır ) x = - 1 için f ( - 1 ) = 3. ( -1 ) = - 3 ( -1 ' in görüntüsü -3 dür ) x = 0 için f ( 0 ) = 3. ( 0 ) = 0 ( 0 ' ın görüntüsü 0 dır ) x = 1 için f ( 1 ) = 3 ( 1 ' in görüntüsü 3 dür ) x = 2 için f ( 2 ) = 3. ( 2 ) = 6 ( 2 ' nin görüntüsü 6 dır ) A -2 -1 0 1 2 -6 -4 -3 0 1 3 6 B a ) Tanım kümesinin bütün elemanları değer kümesinde bir ve yalnız bir elemanla eşlendiği için f bağıntısı bir fonksiyondur. b ) A kümesinin görüntü kümesi f(A)={ – 6, – 3 , 0, 3, 6 } c)f ={(-2, -6), (-1, -3), (0, 0), (1, 3), (2, 6)}

ÖRNEK : 14 f : A → R , f ( x ) = x 2 +1 ve A = { -2 , 0 , 1 , 2 , 3 } ise f ( A ) kaç elemanlıdır? ÇÖZÜM: A = { -2 , 0 , 1 , 2 , 3 } kümesinin görüntülerini bulalım. x = - 2 için f ( -2 ) = ( -2 )2 +1 = 5 elemanlarının x = 0 için f ( 0 ) = ( 0 )2 + 1 = 1 x = 1 için f ( 1 ) = ( 1 )2 + 1 = 2 x = 2 için f ( 2 ) = ( 2 )2 + 1 = 5 x = 3 için f ( 3 ) = ( 3 )2 + 1 = 10 f ( A ) = { 1 , 2 , 5 , 10 } olup s ( f ( A ) ) = 4 tür.

ÖRNEK : 15 f = { ( 2 , 3 ) , ( 4 , 5 ) , ( 6 , 3 ) , ( 8 , 1 ) } bağıntısı bir fonksiyon ise f fonksiyonunun şemasını çizelim , tanım ve görüntü kümelerini yazalım. ÇÖZÜM: Verilen f fonksiyonunun tanım kümesi A , değer kümesi de B olsun. f fonksiyonunun elemanları olan ikililerin birinci bileşenleri tanım kümesinin ( A ) , ikinci bileşenleri de değer kümesinin ( B ) elemanıdır. Buna göre ; f B A Tanım kümesi Değer : A={2, 4, 6, 8 } kümesi : B = { 3 , 5 , 1 } Görüntü kümesi : f( A ) = { 3 , 5 , 1 } 2 4 1 6 3 8 5


ÖRNEK: 17 f ( x +2 ) = 3 x 2 - 2 f(0)+f(3)=? ÇÖZÜM: x +2 = 0 x = - 2 için f ( 0 ) = 3( -2 )2 - 2 f ( 0 ) = 10 f(3)=1 x +2 = 3 x = 1 için f ( 3 ) = 3( 1 )2 - 2 f ( 0 ) + f ( 3 ) = 10 + 1 = 11

ÖRNEK: 18 f( x – 1 ) = 5 x 2 – 4 olduğuna göre f ( 4 ) = ? ÇÖZÜM : x -1 = 4 x = 5 için f(4)=5( )2 – 4 f ( 4 ) = 25 – 4 f ( 4 ) = 21


ÖRNEK: 20 f ( 2 a+2 – 8 ) = 2 a - 2 bulunuz. ise f ( x ) fonksiyonunu ÇÖZÜM: 2 a+2 – 8 = 4. 2 a – 8 = 4. ( 2 a – 2 ) f fonksiyonu , 4 ( 2 a – 2 ) eşlediğine göre f ( 4 x ) = x dir

ÖRNEK: 21 x 2 + 1 f( )= x+ 1 ÇÖZÜM : x 2 + 1 x+ 1 a x+ 1 + 2 x +1 İse x 2 + 1 x+ 1 x 2 + 1 Buna göre f(x)= 1 x + 1 dir. +1 ise f ( x ) = ? 1 a

ÖRNEK: 22 f (x) = 4 x – 7 fonksiyonu veriliyor. f (2 x+3) fonksiyonunun f (x) cinsinden değeri nedir ? ÇÖZÜM: f (2 x+3) = 4( 2 x + 3 ) - 7 = 8 x + 12 - 7 = 8 x + 5 f (x) + 7 =8 ( )+5 4 = 2 f( x ) +14 + 5 = 2 f( x ) + 19 f (x) = 4 x – 7 f (x) + 7 = 4 x f (x) + 7 x= 4

199 2 ÖRNEK: 23 olduğuna göre f ( x – 1 )’ in f ( x ) türünden değeri aşağıdakilerden hangisidir ? ÇÖZÜM : O halde x ‘ i = f ( x ) ’ e bağlı yazarsam sonuca varılır.

x = f ( x ). x + f ( x ) x -xf(x)=f(x) x(1 -f(x))=f(x) Buradan; - - = -


ÖRNEK : 24 f(x)= x 3 . f ( x +1) ÇÖZÜM: ve f ( 5 ) = 9 16 ise f ( 2 ) kaçtır? x =4 için f ( 4 ) = 4 3 . f(5) = 4 3 . 9 16 x =3 için f ( 3 ) = 3 3 . f(4) = 3 3 . 3 4 x =2 için f ( 2 ) = 2 3 . f(3) = 2 3 . 3 4 = 1 2

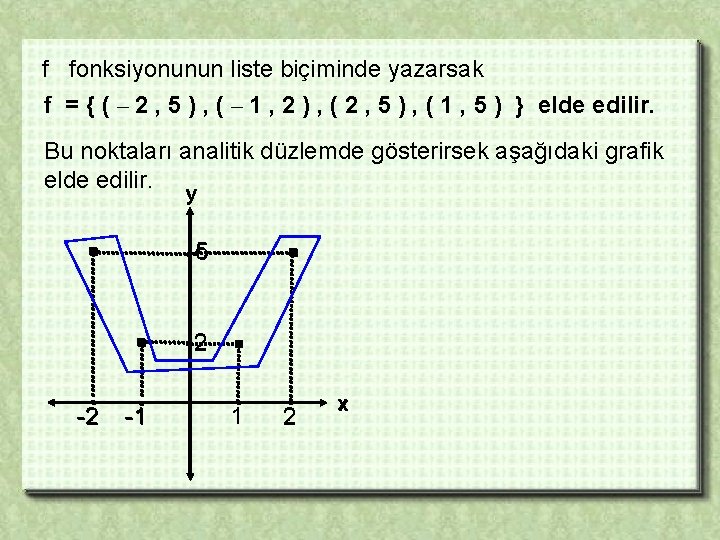
FONKSİYONUN GRAFİĞİ Bir f fonksiyonunun elemanları olan ikilileri analitik düzlemde göstererek oluşturulan noktalar kümesine bu fonksiyonun grafiği denir. ÖRNEK : 25 A = {– 2 , – 1 , 2 } ve A dan B ye f : x x 2 + 1 f ’ nin grafiğini çiziniz. B = { 1 , 2 , 5 } kümeleri ile fonksiyonu verilsin. ÇÖZÜM : A = { – 2 , – 1 , 2 } tanım kümesinin elemanlarının f fonksiyonuna göre görüntüleri ; f ( – 2 ) = ( – 2 )2 + 1 = 5 f ( – 1 ) = ( – 1 )2 + 1 = 2 f ( 2 ) = 22 + 1 = 5 f ( 1 ) = 12 + 1 = 2

f fonksiyonunun liste biçiminde yazarsak f = { ( – 2 , 5 ) , ( – 1 , 2 ) , ( 2 , 5 ) , ( 1 , 5 ) } elde edilir. Bu noktaları analitik düzlemde gösterirsek aşağıdaki grafik elde edilir. y . . . -2 . . 5 . -1 . 2 . . 1 . 2 x

ÖRNEK: 26 f: R R , f ( x ) = 3 x + 1 olduğuna göre f ( x ) ‘ in grafiğini çiziniz. y ÇÖZÜM. 7 Tanım kümesinin elemanlarından bazılarının görüntülerine bakalım. . 4 f ( 0 ) = 3. 0 +1 = 1 f ( 1 ) = 3. 1 + 1 = 4 f ( 2 ) = 3. 2 + 1 = 7 1 . . -2 -1 f = {…. ( 0 , 1 ) , ( 1 , 4 ) , ( 2 , 7 ) , …. } Bu noktalar kümesi yandaki grafiği oluşturur. . 1 . 2 x

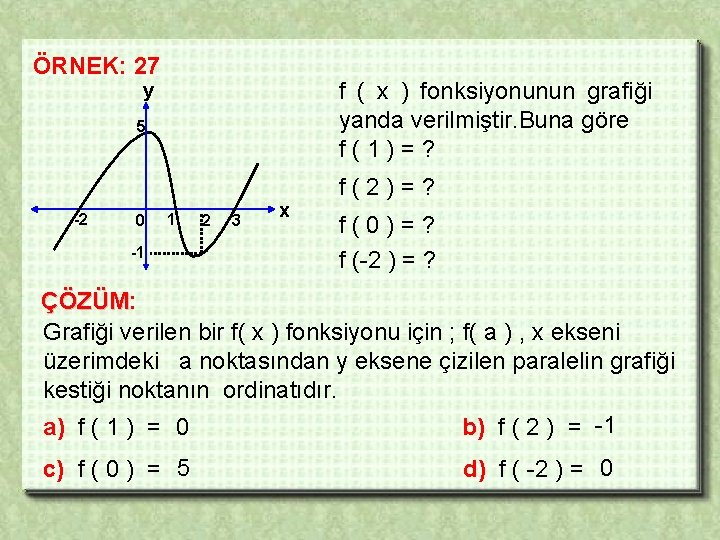
ÖRNEK: 27 f ( x ) fonksiyonunun grafiği yanda verilmiştir. Buna göre f(1)=? y 5 -2 0 1 -1 2 3 x f(2)=? f(0)=? f (-2 ) = ? ÇÖZÜM: ÇÖZÜM Grafiği verilen bir f( x ) fonksiyonu için ; f( a ) , x ekseni üzerimdeki a noktasından y eksene çizilen paralelin grafiği kestiği noktanın ordinatıdır. a) f ( 1 ) = 0 b) f ( 2 ) = -1 c) f ( 0 ) = 5 d) f ( -2 ) = 0

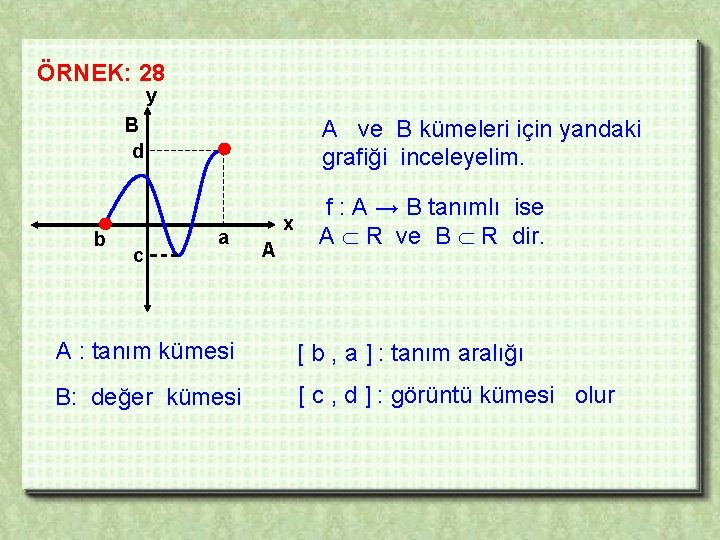
ÖRNEK: 28 y B d b c A ve B kümeleri için yandaki grafiği inceleyelim. a x A f : A → B tanımlı ise A R ve B R dir. A : tanım kümesi [ b , a ] : tanım aralığı B: değer kümesi [ c , d ] : görüntü kümesi olur

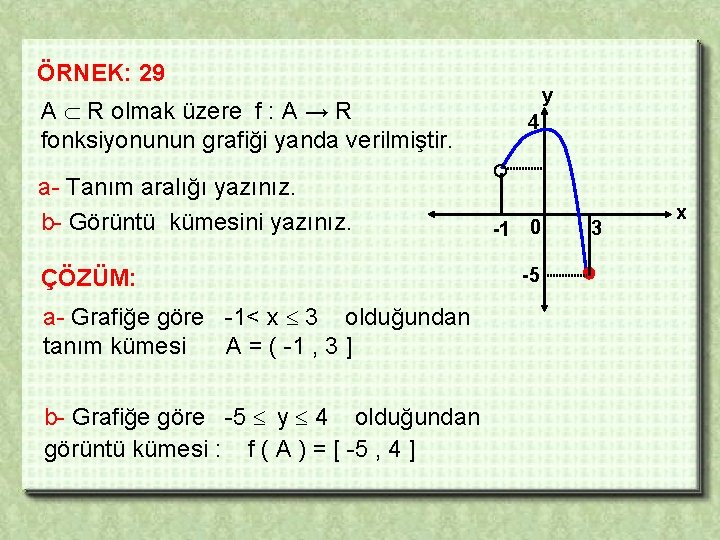
ÖRNEK: 29 A R olmak üzere f : A → R fonksiyonunun grafiği yanda verilmiştir. a- Tanım aralığı yazınız. b- Görüntü kümesini yazınız. ÇÖZÜM: a- Grafiğe göre -1< x 3 olduğundan tanım kümesi A = ( -1 , 3 ] b- Grafiğe göre -5 y 4 olduğundan görüntü kümesi : f ( A ) = [ -5 , 4 ] y 4 -1 0 -5 3 x

ÖRNEK : 30 Grafiği verilen f ( x ) fonksiyonu çin f ( x + 2 ) = 0 eşitliğini sağlayan x değerlerinin toplamı kaçtır? 4 -3 2 3 4 -2 ÇÖZÜM: f(– 3 )=0 , f( 2 )=0 , f( 4 )=0 Buna göre f( x + 2 ) = 0 ise x +2 =– 3 Buradan x = – 5 bunların toplamı , x+2 =2 , , x+2= 4 x = 0 , x = 2 elde edilir – 5 +2=-3 ve

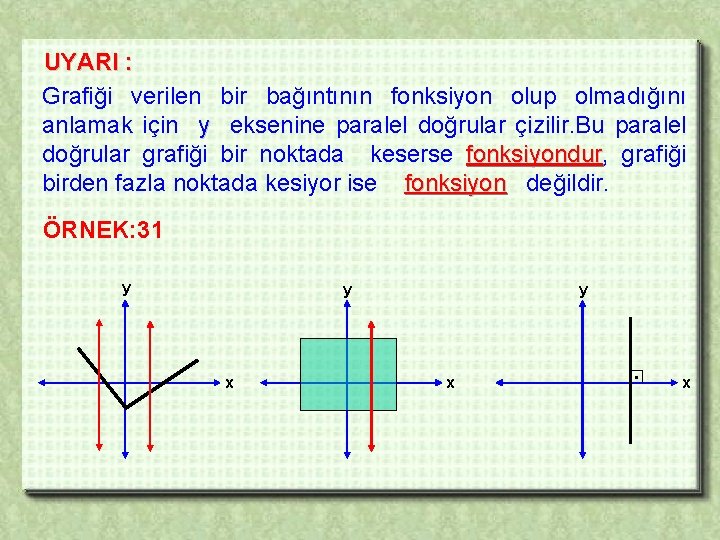
UYARI : Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için y eksenine paralel doğrular çizilir. Bu paralel doğrular grafiği bir noktada keserse fonksiyondur, fonksiyondur grafiği birden fazla noktada kesiyor ise fonksiyon değildir. ÖRNEK: 31 y y x . x

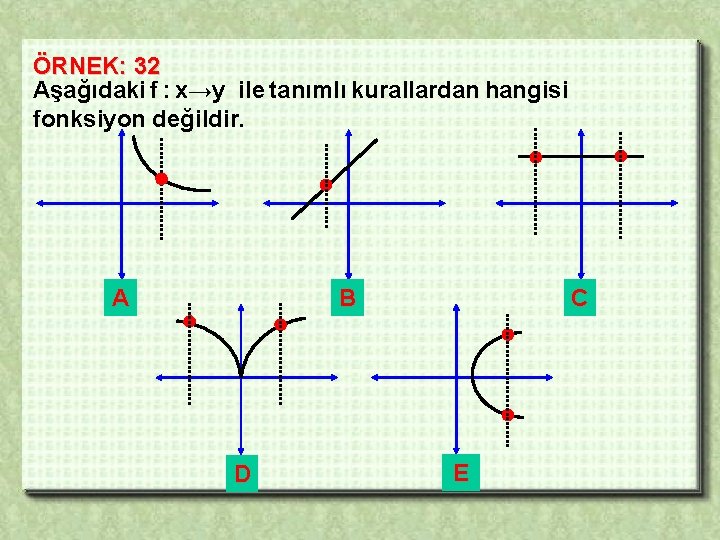
ÖRNEK: 32 Aşağıdaki f : x→y ile tanımlı kurallardan hangisi fonksiyon değildir. A B D C E

FONKSİYON TÜRLERİ : 1 - BİREBİR (1: 1) FONKSİYON Tanım kümesindeki her farklı elemanın , görüntüsü de farklı ise bu tip fonksiyona bire bir ( 1: 1 ) fonksiyon denir. ÖRNEK: 33 f G a b c . 1 F . 2. 3. 4 f fonksiyonu birebirdir g G F . b . 1. 2 . c . 3 . a g fonksiyonu birebir değildir.

ÖRNEK: 34 s(A) = 3 , s( B ) = 5 ise A’ dan B’ ye tanımlanabilecek bire bir fonksiyon sayısı nedir ? ÇÖZÜM: s( A ) = 3 , s( B ) = 5 olduğuna göre A’dan B’ye tanımlanabilecek 1: 1 ve örten fonksiyon sayısı P( m ; n ) = P( 5 ; 3 ) = m! ( m – n )! dir. Buna göre ; 5! 5. 4. 3. 2! = = 60 2! ( 5 – 3 )!

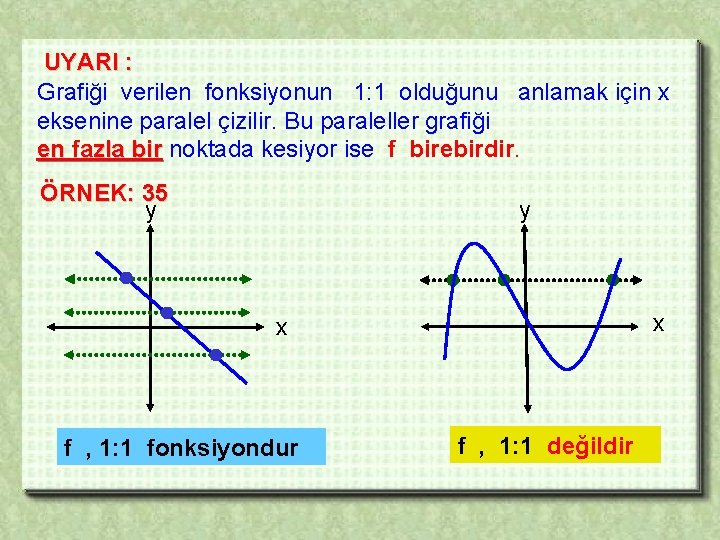
UYARI : Grafiği verilen fonksiyonun 1: 1 olduğunu anlamak için x eksenine paralel çizilir. Bu paraleller grafiği en fazla bir noktada kesiyor ise f birebirdir. ÖRNEK: 35 y y x x f , 1: 1 fonksiyondur f , 1: 1 değildir

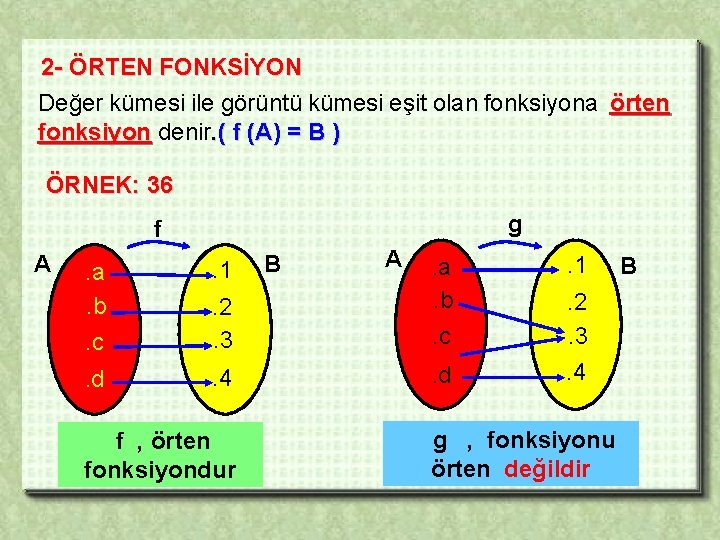
2 - ÖRTEN FONKSİYON Değer kümesi ile görüntü kümesi eşit olan fonksiyona örten fonksiyon denir. ( f (A) = B ) ÖRNEK: 36 g f A . a. b. c. d B A . 1 . 2. 3 . a. b. c . 2. 3 . 4 . d . 4 . 1 f , örten fonksiyondur g , fonksiyonu örten değildir B

3 - İÇİNE FONKSİYON Değer kümesi ile görüntü kümesi birbirinden farklı olan fonksiyona içine fonksiyon denir. ( f (A) B ) ÖRNEK: 37 k h G . a. b. c. d F. 1. 2. 3. 4 h , fonksiyonu içinedir G. a. b. c. d . 1. 2. 3. 4 k , fonksiyonu içine değildir F

ÖRNEK: 38 s(A) = 3 , ve A’ dan A’ ya tanımlanabilecek bire bir ve örten olmayan fonksiyon sayısı nedir ? ÇÖZÜM: s( A ) = 3 A ’ dan A ’ ya tanımlanabilecek 1: 1 ve örten olmayan fonksiyon sayısı ( içine ) mm - m!. dir Buradan 33 - 3! = 27 – 6 = 21

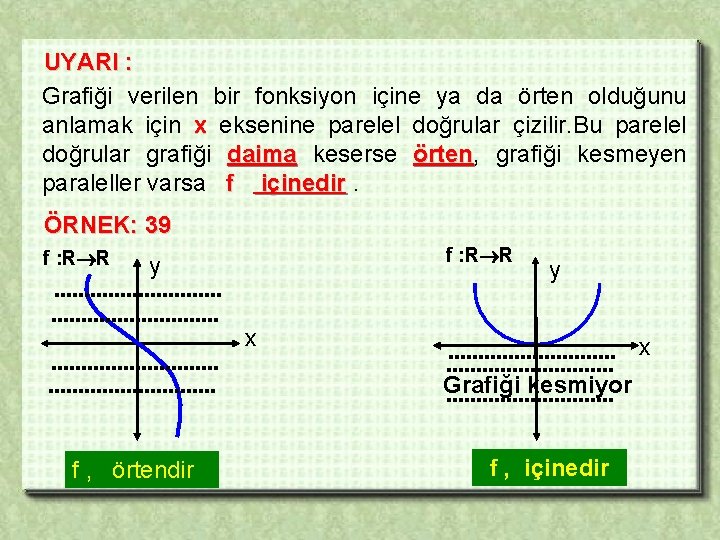
UYARI : Grafiği verilen bir fonksiyon içine ya da örten olduğunu anlamak için x eksenine parelel doğrular çizilir. Bu parelel doğrular grafiği daima keserse örten, örten grafiği kesmeyen paraleller varsa f içinedir. ÖRNEK: 39 f : R R y y x x Grafiği kesmiyor f , örtendir f , içinedir

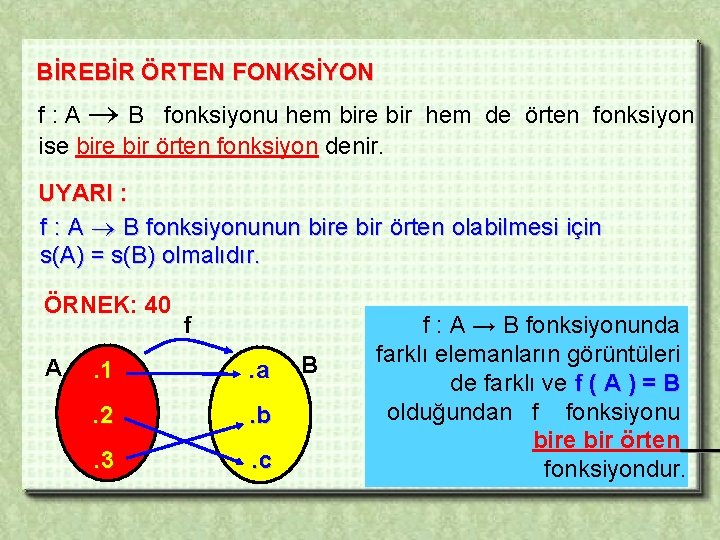
BİREBİR ÖRTEN FONKSİYON f : A B fonksiyonu hem bire bir hem de örten fonksiyon ise bir örten fonksiyon denir. UYARI : f : A B fonksiyonunun bire bir örten olabilmesi için s(A) = s(B) olmalıdır. ÖRNEK: 40 A f . 1 . a . 2 . b . 3 . c B f : A → B fonksiyonunda farklı elemanların görüntüleri de farklı ve f ( A ) = B olduğundan f fonksiyonu bire bir örten fonksiyondur.

UYARI: s( A ) =n ve s( B ) = m olmak üzere A dan B ye tanımlanabilen bire bir ve örten fonksiyon sayısı n ! dir.

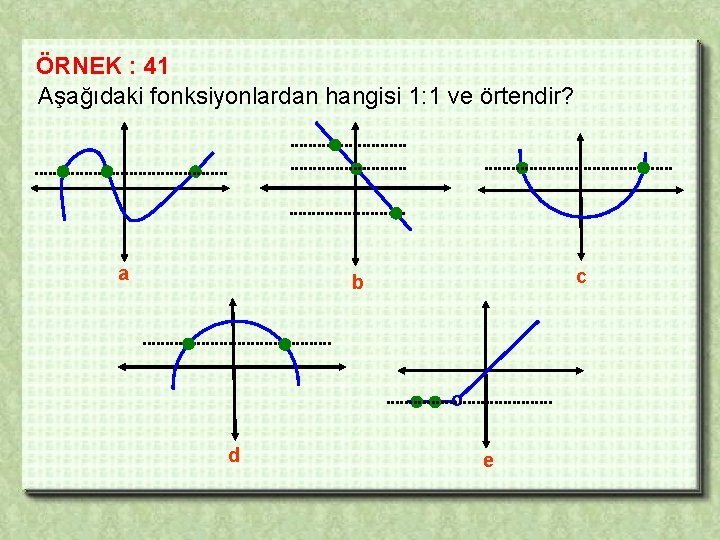
ÖRNEK : 41 Aşağıdaki fonksiyonlardan hangisi 1: 1 ve örtendir? a c b o d e

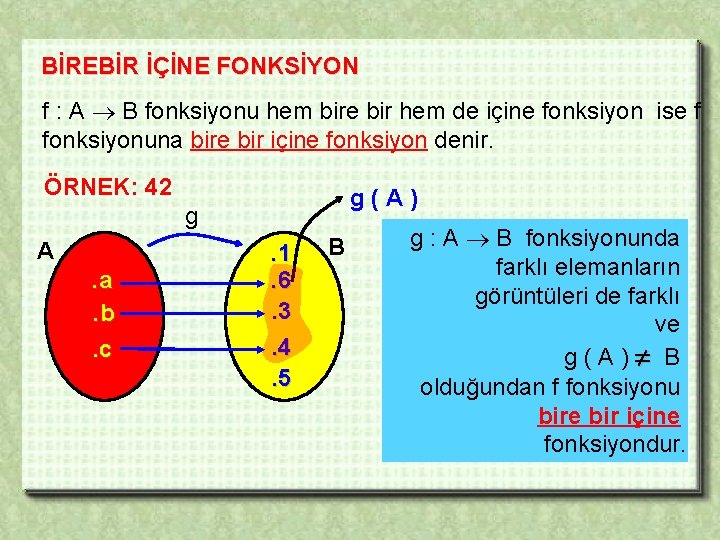
BİREBİR İÇİNE FONKSİYON f : A B fonksiyonu hem bire bir hem de içine fonksiyon ise f fonksiyonuna bire bir içine fonksiyon denir. ÖRNEK: 42 g(A) g A. a. b. c . 1. 6. 3. 4. 5 B g : A B fonksiyonunda farklı elemanların görüntüleri de farklı ve g(A) B olduğundan f fonksiyonu bire bir içine fonksiyondur.

ÖRNEK : 43 Aşağıdaki şemalarla belirtilmiş fonksiyonların hangi türleri tanımladığını söyleyiniz. f A g B . a. b. c. d . 1. 2. 3 C D . k . 1. 2. 3 . f. r. n a) b) İçine fonksiyon Örten fonksiyon

g f E. p . 1 F. 2. 3. 4 . r. s F c) Bire bir içine fonksiyon h M . k. l. m . 0. 1 H . 2 d) Bire bir örten fonksiyon . a. b. 1. c. 2. d. 3. e. f e) Örten fonksiyon N

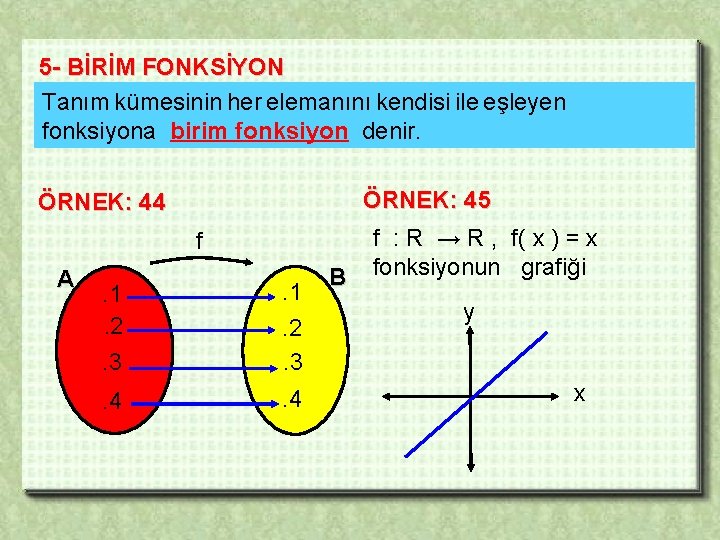
5 - BİRİM FONKSİYON Tanım kümesinin her elemanını kendisi ile eşleyen fonksiyona birim fonksiyon denir. ÖRNEK: 45 ÖRNEK: 44 f A . 1. 2. 3 . 1 . 4 . 2. 3 B f : R → R , f( x ) = x fonksiyonun grafiği y x

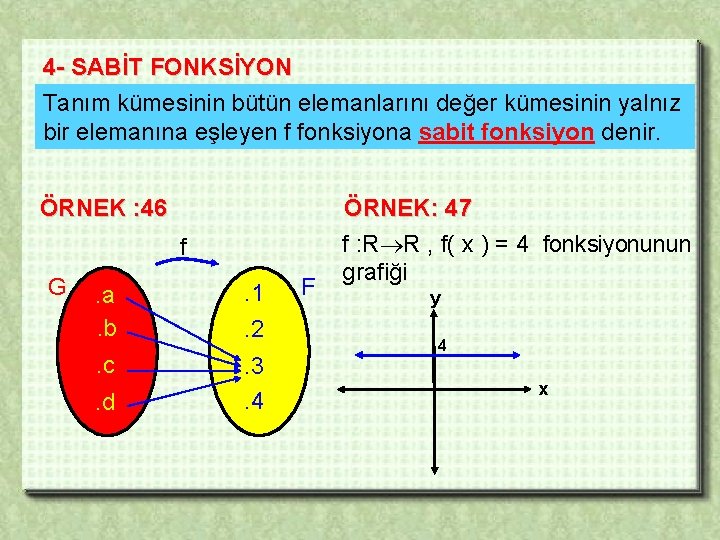
4 - SABİT FONKSİYON Tanım kümesinin bütün elemanlarını değer kümesinin yalnız bir elemanına eşleyen f fonksiyona sabit fonksiyon denir. ÖRNEK : 46 f G . a. b . 1 . c . 3. 4 . d . 2 F ÖRNEK: 47 f : R R , f( x ) = 4 fonksiyonunun grafiği y 4 x

UYARI: s( A ) =n ve s( B ) = m olmak üzere A dan B ye tanımlanabilen sabit fonksiyon sayısı m dir.

SIFIR FONKSİYONU f : A B ye y = f ( x ) fonksiyonunda , 0 B ve x A için f ( x ) = 0 ise fonksiyonu denir. fonksiyona , sıfır Sıfır fonksiyonu sabit fonksiyondur. ÖRNEK: 48 f : R R , f ( x ) = 0 ise f fonksiyonu , denklemi y = 0 olan doğrudur. y Bu doğru x eksenidir x

İKİ HANELİ 50 YE TAKIN SAYILARIN KARESİNİ 10 SANİYE İÇİNDE ALABİLECEK BİR YÖNTEM ÖRNEK : 49 462 = ? ÇÖZÜM: ( 50 – 46 )2 = 42 = 16 46 – 25 = 21 21. 100 = 2100 + 16 = 2116

ÖRNEK: 50 f ( x ) = ( m – 3 )x – 3 ile tanımlı f fonksiyonunun sabit fonksiyon olması için m kaç olmalıdır? ÇÖZÜM f ( x ) fonksiyonunun sabit fonksiyon olması için f x ) = c ( c sabit ) O halde m - 3 = 0 m = 3 için f fonksiyonu sabit fonksiyon olur. Yani; f ( x ) = ( 3 - 3)x – 3 = -3

ÖRNEK: 51 f : N N , x f ( x ) = ( m – 2 )x + 1 - n fonksiyonunun özdeşlik( birim ) fonksiyonu olduğuna göre m+n=? ÇÖZÜM f( x ) fonksiyonunun birim fonksiyon olması için f( x ) = x olmalıdır. Buna göre ; m-2= 1 m= 3 ve 1–n = 0 n = 1 olmalıdır. Buna göre m + n = 3 + 1 = 4 elde edilir.

EŞİT FONKSİYONLAR f : A B ve g : A B iki fonksiyon olsun. x A için f (x) = g (x) ise f ve g fonksiyonlarına eşit fonksiyonlar denir. ÖRNEK: 52 A = { 0, 3 } dan B = { 2, 83 } ye tanımlı f(x) = 3 x 3+ 2 ve g(x) = 9 x 2 + 2 fonksiyonlarının eşit olup olmadığını gösterelim. ÇÖZÜM: f (0) = 3. 03 + 2 = 2 f (3) = 3. 33 + 2 = 83 g (0) = 9. 02 + 2 = 2 f (0) = g (0) g (3) = 9. 32 + 2 = 83 f (3) = g (3) olduğu için f = g dir.

DENK KÜMELER Boş olmayan A ve B kümeleri verilsin , f : A B bire bir ve örten bir fonksiyon ise A kümesi ile B kümesi , denk kümelerdir denir ve A B ile gösterilir. ÖRNEK : 53 A A= {1 , 2 , 3 } kümesi ile B = { a , b , c } kümesinin denk kümeler olduğunu gösterelim. f. 1. 2. 3 B. a. b. c ÇÖZÜM: f ( 1 ) = a , f ( 2 ) = b , f ( 3 ) = c olacak biçimde , f : A B bire bir ver örten fonksiyonu tanımlanabilir. O halde A kümesi ile B kümesi birbirine denk kümelerdir ( A B ) ve s (A ) = s ( B )

11 ve 7 dakikalık zaman dilimini ölçen iki kum saatini kullanarak 15 dakikayı nasıl ölçeriz.

TERS FONKSİYON ÖRNEK: 54 I S A X f Y S O D UYARI: Ters fonksiyonun , bir f fonksiyonun yaptığı işin tersini yaptığını unutmayalım. f-1

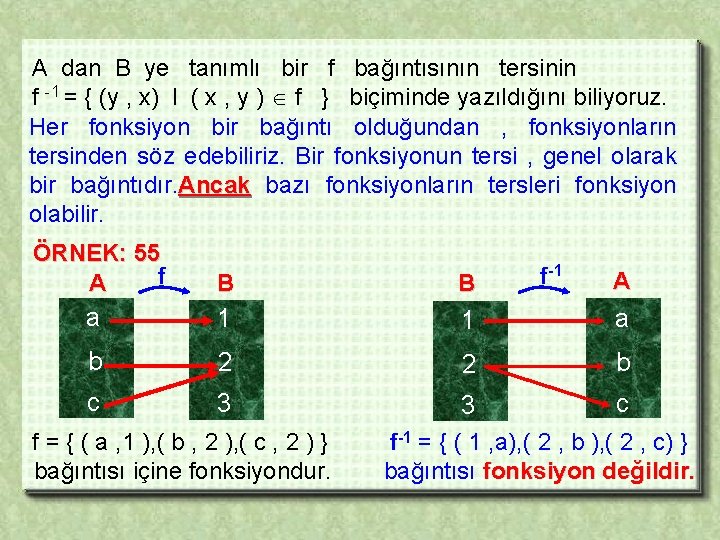
A dan B ye tanımlı bir f bağıntısının tersinin f -1 = { (y , x) l ( x , y ) f } biçiminde yazıldığını biliyoruz. Her fonksiyon bir bağıntı olduğundan , fonksiyonların tersinden söz edebiliriz. Bir fonksiyonun tersi , genel olarak bir bağıntıdır. Ancak bazı fonksiyonların tersleri fonksiyon olabilir. ÖRNEK: 55 f A B B a 1 1 a b 2 2 b c 3 3 c f = { ( a , 1 ), ( b , 2 ), ( c , 2 ) } bağıntısı içine fonksiyondur. f-1 A f-1 = { ( 1 , a), ( 2 , b ), ( 2 , c) } bağıntısı fonksiyon değildir.

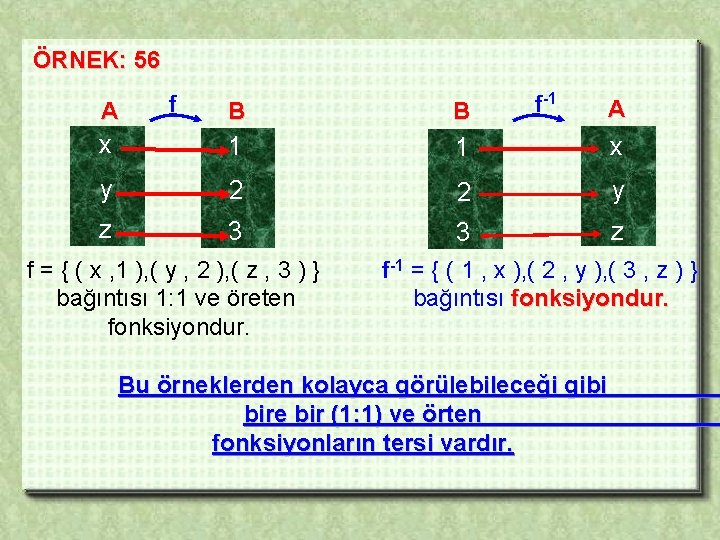
ÖRNEK: 56 A f f-1 A B B x 1 1 x y 2 2 y z 3 3 z f = { ( x , 1 ), ( y , 2 ), ( z , 3 ) } bağıntısı 1: 1 ve öreten fonksiyondur. f-1 = { ( 1 , x ), ( 2 , y ), ( 3 , z ) } bağıntısı fonksiyondur. Bu örneklerden kolayca görülebileceği gibi bire bir (1: 1) ve örten fonksiyonların tersi vardır.

TANIM: f : A → B ye f : x → y = f( x ) fonksiyonu birebir ve örten fonksiyon olmak üzere , f -1 : y → x = f -1( y ) fonksiyonuna f fonksiyonunun tersi denir. UYARI: A B f x y f-1 1 - f : A→B fonksiyonu 1: 1 ve örten ise f(x)=y f-1(y)=x dır. 2 - ( f -1 )-1 = f

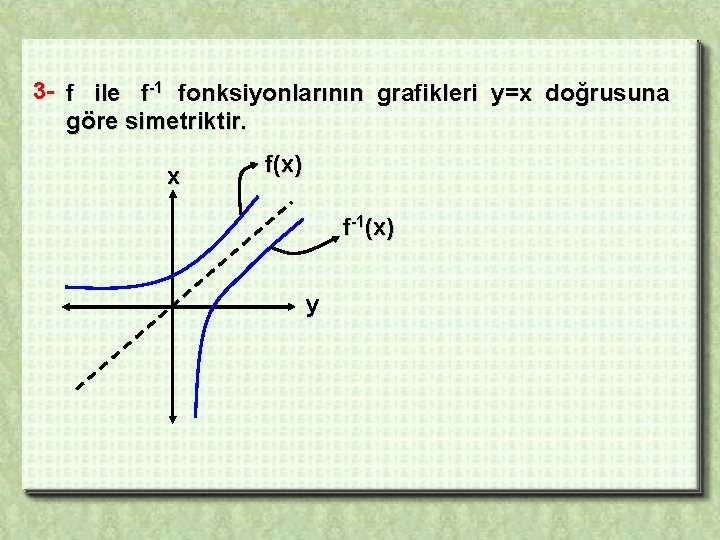
3 - f ile f-1 fonksiyonlarının grafikleri y=x doğrusuna göre simetriktir. x f(x) f-1(x) y

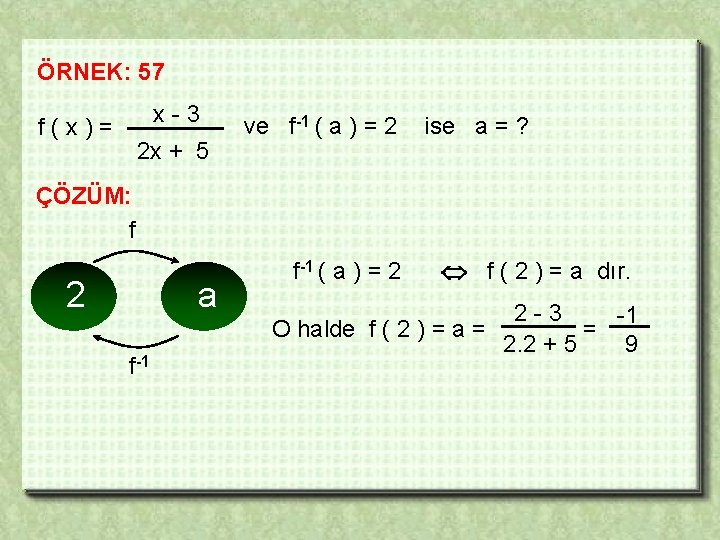
ÖRNEK: 57 x-3 f(x)= 2 x + 5 ve f-1 ( a ) = 2 ise a = ? ÇÖZÜM: f 2 a f-1 ( a ) = 2 f ( 2 ) = a dır. 2 -3 -1 O halde f ( 2 ) = a = = 9 2. 2 + 5

BAZI FONKSİYONLARIN OLARAK BULUNUŞU x 1 - f(x) = a x ise f-1 = a TERSLERİNİN PRATİK , (a 0) 2 - f(x) = x + a ise f-1 = x – a 3 - f(x) = ax + b 4 - R – { - d / c } ise f-1 = x–b a , (a 0) �R – {– a / c } – dx + b ax + b -1 ise f ( x ) = f( x ) = cx + d dx – a 5 - Genel olarak yukarıda ki kurallara uymayan fonksiyonların terslerini bulmak için y yerine x , x yerine y yazılarak y değeri yalnız bırakılır.

ÖRNEK: 58 Aşağıdaki fonksiyonların terslerini bulunuz. a) y = 2 x f -1( x ) = x 2 b) y = 2 x -3 f -1( x ) = x+3 2 y = 3 x + 5 f -1( x ) = x-5 3 c)

d) f(x) = e) f(x) = f) f(x) = g) f(x) = -x-5 3 x+2 f -1( x ) = 2 -3 x f -1( 5 -x x 3 -x 3 x-1 2 -2 x - 5 3 x + 1 - 5 x + 2 x) = -x + 3 x) = -3 x -x+1 -2 x-1 -3

ÖRNEK: 59 f : R R f ( x ) =2 x - 4 ise f-1( x ) = ? ÇÖZÜM: y = f ( x ) =2 x - 4 ifadesinde x ile y’ nin yerlerini değiştirelim ve y yi çekelim. y = 2 x – 4 x = 2 y – 4 y= x+4 2 = f-1 ( x )

ÖRNEK : 60 f : R R f ( x ) =x 7 – 48 ise f-1( x ) = ? ÇÖZÜM: y = f ( x ) = x 7 – 48 ifadesinde x ile y ' nin yerlerini değiştirelim ve y ' yi çekelim. y = x 7 – 48 x = y 7 – 48 x + 48 = y 7 = = = f-1( x)

ÖRNEK: 61 f: [ 2 , ) R , f ( x ) = x 2 - 4 x + 7 olduğuna göre f -1 ( x ) =? ÇÖZÜM f ( x ) = y = x 2 - 4 x + 7 x = y 2 – 4 y + 7 ; x ile y yer değişti x = y 2 – 4 y + 4 – 4 + 7 ; 4 eklenip 4 çıkarıldı x = ( y – 2 )2 + 3 x - 3 = ( y – 2 )2

ÖRNEK : f : R R , f ( x ) = a ne olmalıdır? ax +1 x -4 f(x)=f -1 ( x ) olması için ÇÖZÜM: ax +1 f(x)= x-4 ise f -1 ( x ) = 4 x +1 dir. x-a f ( x ) = f -1 ( x ) olması için a = 4 olmalıdır. ax +1 4 x + 1 = x-a x-4

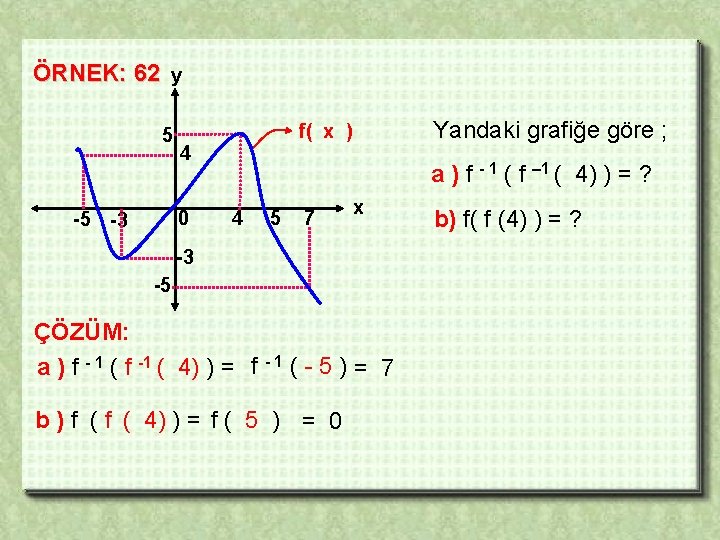
ÖRNEK: 62 y 5 4 0 -5 -3 Yandaki grafiğe göre ; f( x ) a ) f - 1 ( f – 1 ( 4) ) = ? 4 5 7 x -3 -5 ÇÖZÜM: a ) f - 1 ( f -1 ( 4) ) = f - 1 ( - 5 ) = 7 b ) f ( 4) ) = f ( 5 ) = 0 b) f( f (4) ) = ?

ÖRNEK : 63 y f : R R fonksiyonunun grafiği veriliyor. f ( 2 ) + f-1 ( 2 ) kaçtır ? f ( -1 ) + f-1 ( 3 ) f (x) 3 2 1 -1 2 x ÇÖZÜM: Grafiği verilen bir f( x ) fonksiyonu için ; f( a ) , x ekseni üzerimdeki a noktasından y eksene çizilen paralelin grafiği kestiği noktanın ordinatıdır. y 3+0 f ( 2 ) + f-1 ( 2 ) = =1 -1 f ( -1 ) + f ( 3 ) 1+2 f (x) 3 2 1 -1 2 x

ÖRNEK: 64 f ( 3 x – 2 ) = x 2 + 1 ise f(x)=? ÇÖZÜM: 3 x – 2 ’ in tersini eşitliğin sağında x yerine yazılırsa f(x)= = elde edilir.

ÖRNEK: 65 2+3 x f ( 2 x +1 ) = 5 olduğuna göre f (x) = ? 199 2 ÇÖZÜM: 2 x + 1 fonksiyonunun tersi alınıp eşitliğin sağında ve solunda x yerine yazılırsa f( x ) fonksiyonu elde edilir. x– 1 g ( x ) = 2 x + 1 dersek g-1 ( x ) = 2 f(x)=

BİLEŞKE FONKSİYON ÖRNEK : 66 A f g C B gof UYARI: Biz burada , hurda demirin tek fabrikada bileşke fonksiyon diyeceğiz. dönüşmesine. . . . otomobile

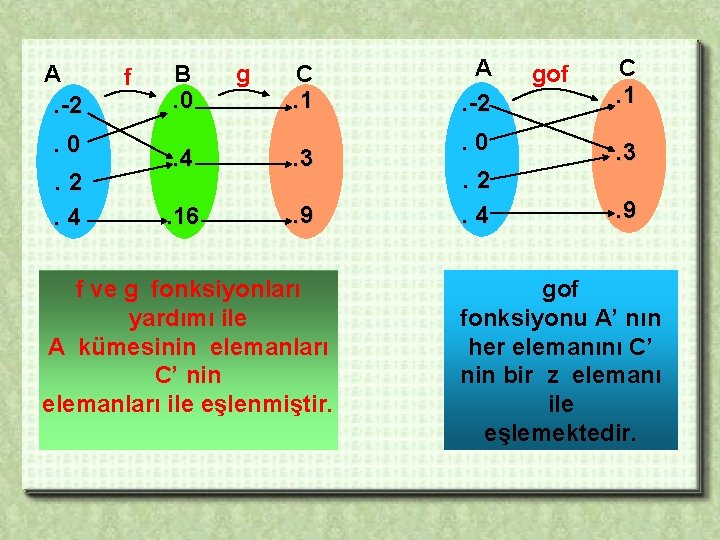
ÖRNEK : 67 A = {– 2 , 0 , 2 , 4 } , B = { 0 , 4 , 16 } , C = { 1 , 3 , 9 } kümeleri ile x f : A B , f (x ) = x 2 , g ( x ) = + 1 fonksiyonlarını 2 şema ile gösterelim. ÇÖZÜM: f ( x ) = x 2 f (– 2 ) = ( – 2 )2 = 4 f ( 0 ) = 02 = 0 g(0 ) = ( 0/2)+1=1 f ( 2 ) = 22 = 4 g(4 ) = ( 4/2)+1=3 f ( 4 ) = 42 = 16 g ( 16 ) = ( 16 / 2 ) + 1 = 9

A. -2. 0. 2. 4 f B. 0 g C. 1 . 4 . 3 . 16 . 9 f ve g fonksiyonları yardımı ile A kümesinin elemanları C’ nin elemanları ile eşlenmiştir. A. -2 gof C. 1 . 0 . 3 . 2. 4 . 9 gof fonksiyonu A’ nın her elemanını C’ nin bir z elemanı ile eşlemektedir.


TANIM: f : A B ye ve g : B C ye fonksiyonları verilsin. f( x ) = y , g ( y ) = z olsun. g o f : C , (gof)(x)=z olan fonksiyona f ile g nin bileşke fonksiyonu denir ve " g o f " yazılışı " g bileşke f " diye okunur. A x f B y=f(x) g C z=g(y) f( f (4) ) = ? gof ( g o f )( x ) = g ( f (x ) ) =g( y ) = z

UYARI: Bileşke fonksiyonda uygulamanın sağdan sola doğru olduğuna dikkat ediniz. ÖRNEK : 68 f ve g , R den R ‘ ye tanımlıdır. f ( x ) = 4 x – 5 ve g ( x ) = x 2 +1 olduğuna göre ( f o g )( x ) ve ( g o f ) ( x ) fonksiyonlarını bulunuz. ÇÖZÜM: f ( x ) = 4 x – 5 , g ( x ) = x 2 +1 olduğuna göre , ( f o g ) ( x ) = f( g( x ) ) = f (x 2 + 1) = 4( x 2 + 1 ) – 5 = 4 x 2 – 1 ( g o f ) ( x ) = g( f( x ) ) = g( 4 x – 5 ) = ( 4 x – 5 )2 + 1 = 16 x 2 - 40 x + 26


BİLEŞKE FONKSİYONLARIN ÖZELLİKLERİ 1 - f o g g o f ; Değişme özelliği yoktur. 2 - ( f o g ) o h = f o ( g o h ) ; Birleşme özelliği vardır. 3 - f o f-1 = f-1 o f = ( x ) ; Birim fonksiyon 4 - f o = o f = f 5 - (f o g )-1 = g-1 o f-1 6 - f o g = g o f = ( x ) ise f = g-1 veya f-1 = g 7 - a) f o g = h ise g = f-1 o h b) g o f = h ise f = g-1 o h
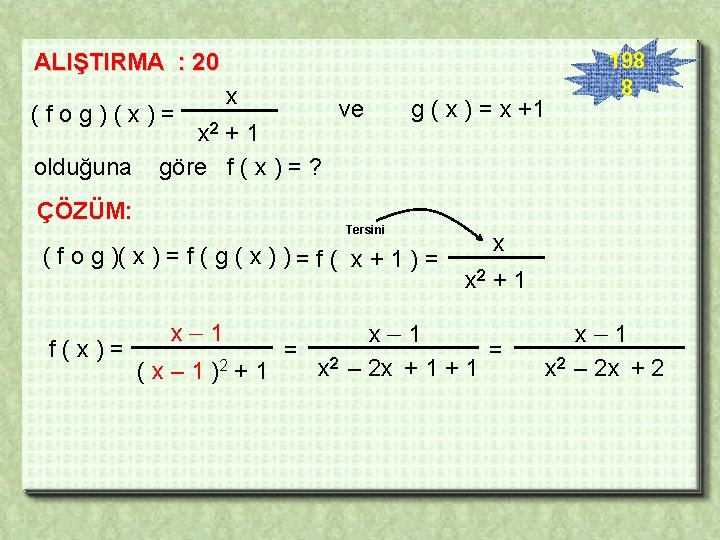
![ÖRNEK 70 f o g 1 o f x ÖRNEK : 70 [ ( f o g )-1 o f ] ( x](https://slidetodoc.com/presentation_image_h/352e99d84891d79d1a90da5165505466/image-96.jpg)
ÖRNEK : 70 [ ( f o g )-1 o f ] ( x ) = 4 x – 7 ise g ( 5 ) = ? ÇÖZÜM: ; Bileşke fonksiyon özelliği -1 o ( f -1 o f ) ; Bileşme özelliği g = ; Bilerim eleman tanımı = g -1 o ( x ) [ ( f o g ) -1 o f ] = g -1 o f = g -1 [(fog) -1 of ]-1= ( g -1 ) -1 = g(5)= 5+7 4 x+7 = 3 4 = g(x)

ÖRNEK: 71 IR den IR ye f ve g fonksiyonları veriliyor. f ( x ) = 2 x + 5 , ( f o g )= 6 x +1 olduğuna göre g(x ) =? ÇÖZÜM : 1. YOL ( f o g )( x ) = 6 x +1 f ( g ( x ) ) = 6 x + 1 2 g ( x ) + 5 = 6 x + 1 2 g ( x ) = 6 x - 4 g ( x ) = 3 x - 2






ÖRNEK : 75 g ( x ) = x 2 – 1 ve f ( x ) = 3 x - 7 ise ( g o f-1 )-1 ( x ) =? ÇÖZÜM: ( gof-1 )-1 ( x ) = [ ( f-1 )-1 o g-1 ] (x ) ; Bileşke fonksiyon özelliği = ( f o g-1 )(x ) = f ( g-1 ( x ) ) = f( ) = 3 - 7 ; g-1( x ) =

ÖRNEK: 76 ise ÇÖZÜM: (fofo. . . of) (x) = ? f (x) = 4 x 10 tane ( f o f ) ( x ) = 4. ( 4 x ) = 42. x ( f o f ) ( x ) = 4. ( 42. x ) = 43. x ( f o f o f ) ( x ) = 4. ( 43. x ) = 44. x . . ( f o f o. . . o f) ( x ) = 4. ( 49. x ) = 410. x 10 tane


ÖRNEK: 78 f ( x ) = ax + b , g ( x ) = 3 x - 1 fonksiyonları veriliyor. ( f o g ) =( g o f ) ( x ) olması için a ve b arasındaki bağıntı ne olmalıdır. ÇÖZÜM : ( f o g ) =( g o f ) ( x ) = x olması halinde eşitlik sağlanır. O halde f o f-1 = ( x ) = x olduğundan g-1( x ) = f ( x ) olmalıdır. Buradan f(x)= x+1 = ax + b a = b = 3 1 3

PERMÜTASYON FONKSİYON Tanım: A A tanımlanan birebir ve örten her fonksiyona permütasyon fonksiyon denir. s(A) = n ise n! kadar permütasyon fonksiyon vardır. ÖRNEK: 79 A={1, 2 , 3 , 4 } , f : A A f = {(1, 3) , ( 2 , 1) , ( 3, 4 ) , (4, 2)} fonksiyonu permütasyon fonksiyondur ve f= 1234 3142 Tanım Kümesi şeklinde gösterilir. Değer Kümesi

ÖRNEK : 80 A ={1, 2, 3, 4 } kümesinde tanımlı f ve g fonksiyonları f = 1234 3421 g= 1234 4312 ise b) g(3)=? a) f(2)=? c ) f fonksiyonunun tersini yazınız. d ) g fonksiyonunun tersini yazınız. ÇÖZÜM: a) f= 1234 3421 f fonksiyonunda 2 , 4 ile eşlendiğinden f ( 2 ) = 4

f = b) g = 1234 3421 g= 1234 4312 g fonksiyonunda 3 , 1 ile eşlendiğinden g( 3 ) = 1 c) f-1 = 1234 4 31 2 d) g-1 = 1234 3 42 1

ÖRNEK : 81 A ={a, b , c , d } kümesinde tanımlı f ve g fonksiyonları f = abcd cabd g= abcd dcab ise ( f o g ) = ? ÇÖZÜM: (fog)= = abcd cabd o abcd dcab ; d b a abcd c b a c c b d bca a d d

ÖRNEK: 82 A = { 1 , 2 , 3 , 4 } kümesinde tanımlı f ve g fonksiyonları f = 1234 2143 ve g = 1234 3124 ise ( f -1 o g ) -1 = ? ÇÖZÜM: ( f-1 o g )-1 = g-1 o ( f -1 )-1 = g-1 o f = 1234 2314 = 1234 3241 o 1234 2143

ÇİFT FONKSİYON VE TEK FONKSİYON : f : R R fonksiyonunda 1 - x R için f ( - x ) = f ( x ) ise f ye çift fonksiyon denir. 2 - x R için f ( - x ) = - f ( x ) ise f ye tek fonksiyon denir. UYARI: Çift fonksiyonların grafikleri y eksenine göre tek fonksiyonların grafikleri ise orijine göre simetriktir.

ÖRNEK : 83 , g( x ) = x 3 + x , h( x ) = x 3 + x 2 f( x ) = x 2 + 3 fonksiyonlarının tek veya çift olup olmadığını araştıralım. ÇÖZÜM: f( -x ) = (-x)2 + 3 = x 2 + 3 = f( x ) olduğu için f çift fonksiyondur. g( -x ) = ( -x )3 + ( -x ) = -x 3 - ( x ) = - (x 3+ x) = - g(x) olduğu için g tek fonksiyondur

h( -x ) = (- x )3 + ( -x )2 = -x 3 + x 2 h( – x ) , h( x )’ e ya da – h( x )’ e eşit olmadığından dolayı , h ne çift ne de tek fonksiyondur.

FONKSİYONLARLA YAPILAN İŞLEMLER f : A R , g : B R fonksiyonları için A ∩ B olsun. 1) f + g : A ∩ B R ( f + g )( x ) = f ( x ) + g ( x ) 2) f – g : A ∩ B R (f–g)(x)=f(x)–g(x) 3) f. g : A ∩ B R ( f. g ) ( x ) = f ( x ). g( x )

4) x ( A ∩ B ) için g(x) ≠ 0 olmak üzere, : A∩B R ( )(x) = 5) c R olmak üzere c. f : A R (c. f)(x) =c. f(x)

ÖRNEK: 84 f : { 1 , 3 } R , f ( x ) = x 2 +2 g : { – 2 , 1 } R , g ( x ) = 2 x – 1 fonksiyonları veriliyor. Buna göre 2 f + g ) fonksiyonunun görüntü kümesini bulunuz. ÇÖZÜM : 2 f + g fonksiyonu { 1, 3 } ∩ { – 2 , 1} = { 1 } kümesinden R’ ye tanımlıdır. Buna göre ; ( 2 f + g ) ( 1 ) = 2 f (1 ) + g ( 1 ) = 2 (12 +2 ) + (2. 1 – 1 ) =6+ 1 =7


ÖRNEK: 86 f = {( 1, 4), (2, 5), (3, 6) } g = { ( 2 , 8 ) , ( 3 , 7 ) , ( 4 , 9 ) , ( 5 , 1 ) } fonksiyonları veriliyor. Buna göre ; a ) 2 f b ) f + g neye eşittir. ÇÖZÜM : a ) 2 f = { ( 1 , 2. 4 ) , ( 2 , 2. 5 ) , ( 3 , 2. 6 ) } = { ( 1 , 8 ) , ( 2 , 10 ) , ( 3 , 12 ) } b ) f + g = { ( 2 , 5+8 ) , ( 3 , 6+7 ) } = { ( 2 , 13 ) , ( 3 , 13 ) } 1 , 4 , 5 tanım kümelerinde ortak eleman olmadığından onlar için dört işlem tanımlı değildir.

BİR FONKSİYONUN EN GENİŞ TANIM KÜMESİ 1 – f ( x ) = anxn + an-1 xn-1 +. . . . . + a 2 x 2 + a 1 x 1 + a 0 x 0 n N , an-1 , . . . a 2 , a 1 , a 0 R biçimindeki fonksiyonlara polinom fonksiyonlar denir. Bu fonksiyonların en geniş tanım kümesi ( aralığı ) Reel sayılardır ( l. R ) ÖRNEK: 87 f ( x ) = x 4 + 7 x 3 - 8 x 2 + 3 polinom geniş tanım kümesi reel sayılar ( R ) dır fonksiyonunun en

2– f ( x ) ve g ( x ) polinom fonksiyonu olmak üzere h( x )= f ( x ) / g ( x ) biçiminde ki ifadelere rasyonel ifadeler denir ve g ( x) = 0 yapan x değerleri varsa h ( x ) ’ in bir fonksiyon olması için bu değerler tanım kümesinden çıkarılmalıdır. ÖRNEK: 88 x 2 + 4 g(x) = bulunuz. x – 2 fonksiyonunun en geniş tanım kümesini ÇÖZÜM: g ( x )’ in paydasını sıfır yapan değer x – 2 = 0 x = 2 dir. O halde tanım aralığı l. R – { 2 } dir.

ÖRNEK: 89 3 f : A B tanımlanan f ( x ) = x-5 ve değer kümesini bulunuz. fonksiyonunun tanım ÇÖZÜM: f ( x ) fonksiyonunun tanım kümesi , paydayı sıfır yapan x değerlerinin kümesinin reel sayılar kümesinden çıkarılmış halidir. x-5 = 0 x=5 olup f ( x ) fonksiyonunun tanım kümesi , IR – { 5 }

3 f : A B tanımlanan f ( x ) = x-5 ve değer kümesini bulunuz. fonksiyonunun tanım f ( x ) fonksiyonunun değer kümesi , f ( x ) fonksiyonunu tersinin tanım kümesidir. f ( x )’ in tersi f -1( x ) = 5 x + 3 dir. x Bu f -1( x ) fonksiyonunun tanım kümesi , paydayı sıfır yapan x değerlerinin kümesinin reel sayılardan çıkarılmış halidir. x=0 Yani , IR – { 0 } O halde f ( x ) fonksiyonunun değer kümesi , IR – { 0 }

3 – f ( x) = ( n Z+ ve ifadelere köklü fonksiyonlar denir. n > 1 ) biçimindeki a- n tek ise f ( x ) in en geniş tanım aralığı R dir. ÖRNEK: 90 f(x) = kümesini bulunuz. fonksiyonunun en geniş tanım ÇÖZÜM : Kök indeksi 9 ( Tek ) olduğundan f ( x ) in en geniş tanım aralığı R dir.

b- n çift ve g(x) < 0 ise f(x) , R de tanımlı olamaz o halde f(x) ’ in R ’ de tanımlı olabilmesi için g(x) 0 olmalıdır. ÖRNEK: 91 g(x) = kümesini bulunuz. fonksiyonunun en geniş tanım ÇÖZÜM : x +9 0 ve x - 9 Çünkü kök derecesi 4 Çift sayıdır. En geniş tanım aralığı [ - 9 , ) dur.


ALIŞTIRMA : 1 f : N N , f (x) = x – 10 g : Z Z , g (x) = (x+1) / 2 h : R R , h (x) = x 2 bağıntılarının hangileri fonksiyondur? ÇÖZÜM: f fonksiyon değildir. Çünkü 2 N olmasına rağmen f ( 2 ) = 2 – 10 = – 8 N dir. ( yani 2 nin görüntüsü yoktur. ) g fonksiyon değildir. Çünkü tanım kümesindeki çift sayıların görüntüleri değer kümesinde yoktur. g ( 10 ) =(10+1) / 2 = ( 11 / 2 ) Z dir. h : R R bir fonksiyondur. Çünkü her bir reel sayıya karşı bir reel sayı karşılık gelmektedir.

ALIŞTIRMA : 2 { 1 , 2 , 3 } kümesinden { 10 , 11 , 12 , }kümesine aşağıdaki fonksiyonlar tanımlanıyor. Bu fonksiyonlardan hangisinin ters fonksiyonu vardır? a) { ( 1 , 11 ) , ( 2 , 10 ) , ( 3 , 12 ) } b) { ( 1 , 12 ) , ( 2 , 11 ) , ( 3 , 11 ) } c) { ( 1 , 10 ) , ( 2 , 10 ) , ( 3 , 10 ) } d) { ( 1 , 10 ) , ( 2 , 10 ) , ( 3 , 11 ) } e) { ( 1 , 12 ) , ( 2 , 11 ) , ( 3 , 12 ) } ÇÖZÜM: ÇÖZÜM Bire bir ve örten fonksiyonların tersi olacağından , doğru cevap A şıkkıdır.

199 8 ALIŞTIRMA : 3 Bir fonksiyonu , " Her bir pozitif tam sayı kendi ile çarpımsal tersinin toplamına götürüyor. “şeklinde tanımlanmıştır. Bu fonksiyon aşağıdakilerden hangisi ile gösterilebilir? x 2 + x A) f ( x ) = x-1 x B) f ( x ) = 2 x -1 x C) f ( x ) = 2 x +1 x 2 - 1 D) f ( x ) = x x 2 + 1 E) f ( x ) = x

ALIŞTIRMA : 4 f : R → R , f ( x ) = ( 4 n - 2 )x + 2 n + 3 fonksiyonu sabit fonksiyondur. Buna göre f ‘ nin kuralını bularak grafiğini çiziniz. ÇÖZÜM: f fonksiyonu sabit fonksiyon olduğuna göre 1 4 n – 2 = 0 4 n = 2 Buna göre ; f(x) = 4 f(x)=4 4

ALIŞTIRMA : 5 ( x ) birim fonksiyon olmak üzere 3 x – 1 f(x)= 5 Buna göre g( , 2 5 ( g o f ) ( x ) = ( x ) dir. ) = ? ÇÖZÜM: ( g o f ) ( x ) = g ( f ( x ) ) = g ( 3 x – 1 ) = x 5 g ( x ) = – 5 x – 1 = 3 x + 1 – 3 5 g( 2 5 )= 3. 2 + 1 = 5 ; (x)=x


ALIŞTIRMA : 7 f(x) = x 3 – 3 x 2 + 3 x -1 olduğuna göre ÇÖZÜM: f ( x ) = x 3 – 3 x 2 + 3 x -1 = ( x - 1 )3 f ( x ) = ( x - 1 )3 f ( x + 1) = ( x + 1 - 1 )3 f ( x + 1) = x 3 199 8 f (x+1) değeri nedir ?



ALIŞTIRMA : 9 198 7 f ( 2 x +3 ) = 3 x + 2 , olduğuna göre f ( 0 ) = ? ÇÖZÜM: 2 x + 3 = 0 2 x = – 3 x= 2 x= – 3 2 için f ( x )= = = – 9 +2 2 – 5 2

ALIŞTIRMA : 10 199 7 f : R R f ( x ) = 2 x + 1 – f ( x +1 ) ve f ( 4 )= 2 olduğuna göre f ( 2 )’ nin değeri nedir ? ÇÖZÜM: x =2 için f ( 2 ) = 4 +1 – f ( 3 ) = 4 +1 – 5 = 0 f(2)=0 x =3 için f ( 3 ) = 6 +1 – f ( 4 ) = 6 + 1 – 2 = 5 f(3)=5

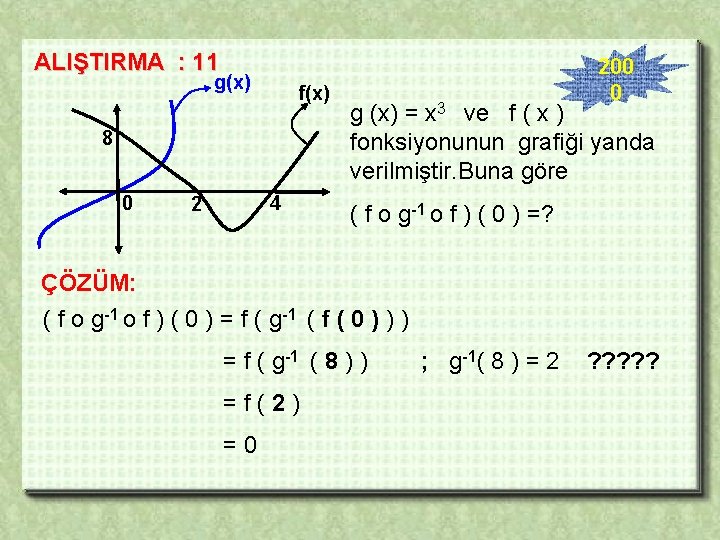
ALIŞTIRMA : 11 g(x) f(x) 8 0 4 2 200 0 g (x) = x 3 ve f ( x ) fonksiyonunun grafiği yanda verilmiştir. Buna göre ( f o g-1 o f ) ( 0 ) =? ÇÖZÜM: ( f o g-1 o f ) ( 0 ) = f ( g-1 ( f ( 0 ) ) ) = f ( g-1 ( 8 ) ) =f(2) =0 ; g-1( 8 ) = 2 ? ? ?

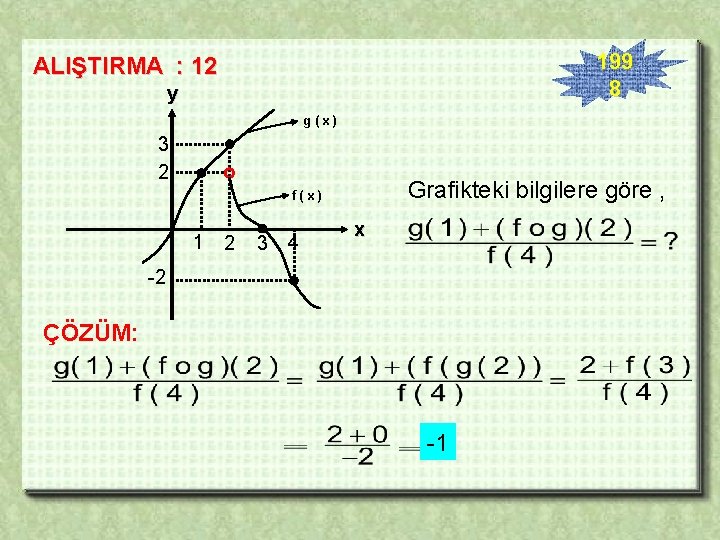
199 8 ALIŞTIRMA : 12 y g(x) 3 2 Grafikteki bilgilere göre , f(x) 1 2 3 4 x -2 ÇÖZÜM: -1

ALIŞTIRMA : 13 y y = f ( x ) fonksiyonunun grafiği yanda verilmiştir. ( f o f ) ( x ) = 4 şartını sağlayan x değerlerinin toplamı kaçtır? 4 -4 0 3 ÇÖZÜM: ( fof )(x)=4 4 x f(f(x))=4 f(x)=0 x 1 =– 4 x 2=3 x 3=4 x=– 4 x=3 x=4 Σx = 3

ALIŞTIRMA : 14 199 8 2 x – 1 fonksiyonunun değer x– 1 kümesi aşağıdakilerden hangisidir ? IR - {1} de tanımlanan f (x) = A) IR B) IR - {3} C) IR - {2} D) IR - {1} E) IR - {0} ÇÖZÜM: f ( x ) fonksiyonunun değer kümesi , f ( x ) fonksiyonunu tersinin tanım kümesidir. x– 1 f ( x )’ in tersi f -1( x ) = x– 2 Bu f -1( x ) fonksiyonunun tanım kümesi , paydayı sıfır yapan x değerlerinin kümesidir. x-2 = 0 x = 2 Yani , IR – { 2 } O halde f ( x ) fonksiyonunun değer kümesi , IR – { 2 }

ALIŞTIRMA : 15 y ( 4 , 13 ) Yanda grafiği verilen fonksiyonun tanım kümesi nedir? (-2, 3) x ÇÖZÜM: Grafiğe göre -2 x 4 Tanım kümesi [ -2 , 4 ] olduğundan tanım kümesi

199 1 ALIŞTIRMA : 16 fonksiyonunun en geniş tanım aralığını bulunuz. ÇÖZÜM: 0 = Bu eşitsizliğin kökleri x -1 + 0 _ + olmalıdır. x + 1 = 0 x = -1 x = 0 Tanım aralığı IR- [ -1 , 0 ] dir. Eşitlik olmasına rağmen x = 0 ve x = -1 niçin tanım aralığında çıkarıldı ?

ALIŞTIRMA : 17 199 0 f ( x ) = 23 x-1 olduğuna göre f (2 x)’ in f( x ) cinsinden ifadesini bulunuz. A) 3 f(x) B) 3[f(x)]2 C) 2 f(x) D) 2[f(x)]2 E) 2[f(x)]3 ÇÖZÜM: f (2 x) = 23. (2 x)-1 = (23 x)2. = (2 f(x))2. =4. (f(x))2. = 2 [ f ( x ) ]2 f (x)= 23 x-1 23 x 2 f(x) = 23 x = 2

ALIŞTIRMA : 18 (fog)(x)= olduğuna x x 2 + 1 göre g ( x ) = ? ve f ( x ) = x +1 198 9 ÇÖZÜM: ( f o g )( x ) = f ( g ( x ) ) = g(x)+1 = g(x) = x x 2 + 1 x – x 2 -1 x 2 + 1 – 1 = – x 2 + x – 1 x 2 + 1

198 9 ALIŞTIRMA : 19 f( x +1 ) = x-2 x +1 ise en uygun koşullar altında f (x) =? ÇÖZÜM: x +1 = u dersek x-2 O halde f(x)= x-2 = x +1 1 x dir. 1 u dur. Yani ; f(u)= 1 u dur.

ALIŞTIRMA : 20 (fog)(x)= olduğuna x x 2 + 1 göre f ( x ) = ? ÇÖZÜM: ve g ( x ) = x +1 Tersini ( f o g )( x ) = f ( g ( x ) ) = f ( x + 1 ) = x– 1 198 8 x x 2 + 1 x– 1 f(x)= = 2 x – 2 x + 1 (x– 1) +1 x– 1 x 2 – 2 x + 2

ALIŞTIRMA : 21 f ( x ) doğrusal fonksiyonu için olduğuna göre f ( 1 ) =? f ( 2 ) =3 198 7 , f(3) =2 ÇÖZÜM : f ( x ) doğrusal fonksiyon olduğuna göre , f ( x ) = ax + b şeklindedir. x = 2 için f ( 2 ) = 2 a + b 3 = 2( -1) + b 5 = b x = 3 için f ( 3 ) = 3 a + b O halde f ( x ) = -x + 5 dir 3 = 2 a + b - 2 = - 3 a + b 1 = -a a = -1 Buradan f ( 1 ) = -1 + 5 = 4 olur.

ALIŞTIRMA : 22 f ( x-5 2 x - 1 ) -2 x + 3 = x+1 ise ÇÖZÜM: x = 0 için -2( 0 ) + 3 f(5 ) = 0+1 = 3 f (5 ) =?

198 1 ALIŞTIRMA : 23 f : R R , f ( x ) = -2 x biçiminde verilen bir fonksiyondur. x+a f ( x ) = f -1 ( x ) olması için a ne olmalıdır? ÇÖZÜM: f(x)= -2 x x+a ise f -1( x ) = f ( x ) olması için a = 2 olmalıdır. -1 ( -ax x +2 -2 x = x+a dir. -ax x +2 )

ALIŞTIRMA : 24 f 2 ( x ) – 6 f (x ) + 9 = x 2 + 2 x +1 olduğuna göre f( x ) fonksiyonunu bulunuz. ÇÖZÜM : f 2 ( x ) – 6 f (x ) + 9 = x 2 + 2 x +1 ( f (x ) – 3 )2 = ( x + 1 )2 f (x ) – 3 = f (x ) = x + 1) x+4

ALIŞTIRMA : 25 f ( x 3 – 3 x 2 – 5 ) = 3 x 3 – 9 x 2 + 7 ise f-1( x ) aşağıdakilerden hangisidir? a) x– 5 b ) 3 x + 7 c ) 3 x – 7 d ) ( x + 3 ) / 22 e ) ( x – 22 ) / 3 ÇÖZÜM : x 3 – 3 x 2 – 5 3. ( x 3 – 3 x 2 – 5 ) + 22 = 3 x 3 – 9 x 2 – 15 + 22 = 3 x 3 – 9 x 2 + 7 O halde f ( x ) = 3 x + 22 dir. Buradan f-1( x – 22 x)= 3

Savaş sırasında Genel Kurmay Başkanlığından yüzbaşıya şöyle bir emir geldi : " 214 numaralı tepenin eteğinde 120 erinizi , her sırada 11 er olacak şekilde 12 sıra yapın ve sizin her sıradan eşit uzaklıkta olmanız gerekmektedir " Bu emir yapılabilir mi ?

ALIŞTIRMA 26 : 3 kişinin katıldığı bir sınav , başarı yönünden kaç farklı biçimde sonuçlanabilir ? ÇÖZÜM Sınava katılan 3 kişi A tanım kümesini , sınav sonucuda B kümesini oluştursun. . f. Başarılı. Başarısız A dan B ye 23 tane fonksiyon tanımlandığına göre sınav 8 farklı biçimde sonuçlanabilir.

ALIŞTIRMA : 27 f(x)= 2 x + 1 , x > 2 ise 1 - 2 x , x > 0 ise x - 1 , 0 < x 2 ise g( x ) = , x 0 ise 3 2 - x , x 0 ise ( f + g ) ( x ) fonksiyonunu bulunuz. ÇÖZÜM ( f + g )( x ) = ( 2 x + 1 ) + (1 - 2 x ) , x > 2 ise ( x – 1 ) + ( 1 - 2 x ) , 0 < x 2 ise 3 + (2–x) , x 0 ise

ALIŞTIRMA: 28 f ( x ) = x 3 + x + m şeklinde tanımlanan f fonksiyonunun ters ( f-1 ) fonksiyonuna ait grafik ( 4 , -1 ) noktasından geçtiğine göre m kaçtır ? ÇÖZÜM ( 4 , – 1 ) f-1 ( – 1 , 4 ) f f( – 1 ) = 4 f( – 1 ) = (– 1 )3 – 1 + m = 4 – 1 +m = 4 – 2 +m = 4 m=4+2=6