Complete Search Chapter 8 of the text Complete

Complete Search Chapter 8 of the text

Complete Search • Brute force • Solving a problem by traversing the entire search space in the worst case. • We use this method when we do not know any other approach. • If possible quickly identify some infeasible points in the search space.

Uva 725 • Display all pairs of 5 -digit numbers that collectively use the digits 0, 1, 2 …, 9 once such that the first number divided by the second number is N where 2 ≤ N ≤ 79. – two numbers abcde and fghij such that abcde/fghij = N. – when N = 62, 79546/01283 = 62 – also 94736/01528 = 62.

Uva 725 • Display all pairs of 5 -digit numbers that collectively use the digits 0, 1, 2 …, 9 once such that the first number divided by the second number is N where 2 ≤ N ≤ 79. – two numbers abcde and fghij such that abcde/fghij = N. • When N = 62, 79546/01283 = 62 • Also 94736/01528 = 62.

Uva 725 • We can generate 10! permutations. – For each permutation check if it is a valid pair. • (an improvement) – Generate P(10, 5) permutations fghij. – Check if fghij * N covers all digits exactly once. • Huge savings.

Uva 725 • Even better: – fghij can only range from 01234 to 98765/N (i. e. 100 K possibilities) • for (int fghij = 01234; fghij ≤ 98765/N; fghij++){ – abcde = fghij * N; – if all digits are used, print it. }

Uva 441 • Given 6 < k < 13 integers, enumerate all possible subsets of size 6 in sorted order. • Sorting the elements first will eliminate many possibilities. • Let S be the sorted list of k integers.

Uva 441 • Use nested loops. for (int a = 0; a < k-5; a++) for (int b = a+1; b < k-4; b++) for (int c = b+1; c < k-3; c++) for (int d = c+1; d < k-2; d++) for (int e = d+1; e < k-1; e++) for (int f = e+1; f < k; f++) Print (S[a], S[b], S[c], S[d], S[e], S[f])

Uva 11565 • Given three integers A, B, C (1 ≤ A, B, C ≤ 10000) find three other distinct integers x, y, z such that x + y + z = A; x. y. z = B; and x 2 + y 2 + z 2 = C. • Can generate all 104 x 104 triplets. – (Way too much)

Uva 11565 • Given three integers A, B, C (1 ≤ A, B, C ≤ 10000) find three other distinct integers x, y, z such that x + y + z = A; x. y. z = B; and x 2 + y 2 + z 2 = C. • Can generate all 104 x 104 triplets. – (Way too much) • Since the integers are all distinct, each of the values of x, y and z must lie in the interval [100, 100]. • The number of triplets need to be generated is 8 x 102.

Uva 11565 • Given three integers A, B, C (1 ≤ A, B, C ≤ 10000) find three other distinct integers x, y, z such that x + y + z = A; x. y. z = B; and x 2 + y 2 + z 2 = C. • Further improvement. – Let x be the smallest integer. – if x = y = z, x. y. z < B. – i. e. |x| < B 1/3 – i. e. x lies in [-22, 22].

Exhaustive Recursion • Consider a recursive function that makes not just one recursive call, but several. • Problem: Computing all possible re-arrangement of the letters in a string. • The pseudocode strategy is as follows: – if you have no more characters left to rearrange, print the arrangement for (every possible choice among the characters left to rearrange){ Make a choice and add that character to the permutation so far Use recursion to rearrange the remaining letters }

Permutation Code rest[i] is the next choice. remaining contains everything except the ith character.

Code • In this exhaustive traversal, we try all possible combination. There are n! ways to rearrange the characters in a string of length n, and this prints them all.

Exhaustive subset pattern • At each step, we isolate an element from the remainder and then recursively list those sets that include that set, and recur again to build those sets that don’t contain that element. – if there is no more elements remaining, print current subset else { Consider the next element of those remaining Try adding it to the current subset, and use recursion to build subsets from here. Try not adding it to the current subset, and use recursion to build subsets from here }

Exhaustive subset pattern • • It builds every possible combination of the elements. Each call makes two additional calls and continues to a depth of n. There are 2 n nodes in the decision tree. The overall algorithm is 2 n.

Recursive Backtracking • Exhaustive recursion explores all possible combination. • In both permutation and subset examples we explore every possibility. This can be expensive. • In recursive backtracking, we will try one choice and only undo the decision if it doesn’t work out.

Generic Pseudocode

Changing exhaustive permutation code into a backtracking algorithm • Take a string of letters and attempt to rearrange it into a valid word (as found in our lexicon) • We consult the lexicon to determine, before the recursive call, whether a given permutation is a word. If so, it stops, otherwise continue exploring the other choices.

Changing exhaustive permutation code into a backtracking algorithm

The Eight-Queens Problem • It is a classic problem in computer science. • The goal is to assign eight queens to eight positions on an 8 x 8 chessboard so that no queen, according to the chess rule, can attack any other queen on the board.

In pseudocode our srtategy will be

Uva 750 (8 -queens problem) • Determine all possible 8 -queens solution given that a queen is placed at location (a, b). • No two queens share the same column or same row. • row[i]: row position of the queen in column i. • There are 8! different possibilities.

Uva 750 (8 -queens problem) • Determine all possible 8 -queens solution given that a queen is placed at location (a, b). • No two queens share the same column or same row. . • row[i]: row position of the queen in column i. • We also know that no two queens share any of the two diagonal lines. • If there exists a queen at location (i, j) and a queen at location (k, l), they attack each other diagonally if |i-k| = |j-l|.

Uva 750 (8 -queens problem) • Checking if the placement of a queen at location (r, c) is valid. • bool place(int r, int c){ for (int prev = 0; prev < c; prev++){ if (row[prev] ==r || abs(row[prev] – r) == abs(prev –c)) return false; return true; } }

Uva 750 (8 -queens problem) • void backtrack(int c){ if (c == 8 && row[b] == a) print the solution for (int = 0; r < 8; r++){ if (place(r, c)){ \ yes, a queen can be placed row[c] = r; backtrack[c +1]; } }

Uva 750 (8 -queens problem) • void backtrack(int c){ if (c == 8 && row[b] == a) print the solution for (int = 0; r < 8; r++){ if (place(r, c)){ \ yes, a queen can be placed at (r, c) row[c] = r; backtrack[c +1]; } We need to find a better } way to implement Place()

Uva 750 (8 -queens problem) • Checking if the placement of a queen at location (row, col) is valid. • Maintain thee boolean arrays: – a[1. . 8] <> if a[r] is true, there is a queen placed in row. Otherwise, it is false. – b[2. . 16] <> if b[row+col] is true, location (row, col) is attacked by a queen placed at location (x, y) where x+y = row+col. Otherwise it is false. – c[-7. . 7] <> if c[col-row] is true, location (row, col) is attacked by a queen placed at location (x, y) if col–row = y-x. Otherwise it is false.

Algorithm for the 8 -queen problem

Tips • Trying a complete search is a gamble. – May be ok if the time limit is large (say 10 s!) • Filtering vs Generating – place the queen and eliminate more possibilities – start with all possibilities, and then remove them one by one. (for 8 -queens problem there are 8! possibilities in the search space) – filtering is slower. • Prune away the infeasible/inferior search

Tips • Utilize symmetries. – 8 -queens have 92 solution but with only 12 unique solution – the rest of the solutions are rotational/line symmetries – Generally involves complex coding, not desirable in competitive programming. • Keep it simple and short.

Tips • Try solving an equivalent dual problem. – (Uva 10360) A 2 d-dimensional array (1024 x 1024) containing rats. There are n ≤ 20, 000 rats spread across the cells. Determine which cell (x, y) should be gas bombed so that the number of rats killed in a square box (x – d, y – d) (x + d, y + d) for a given d is maximized.

• Determine for each rat square, the squares where if a bomb is placed will kill the robot. • Number of pixels to be visited will be considerably less.

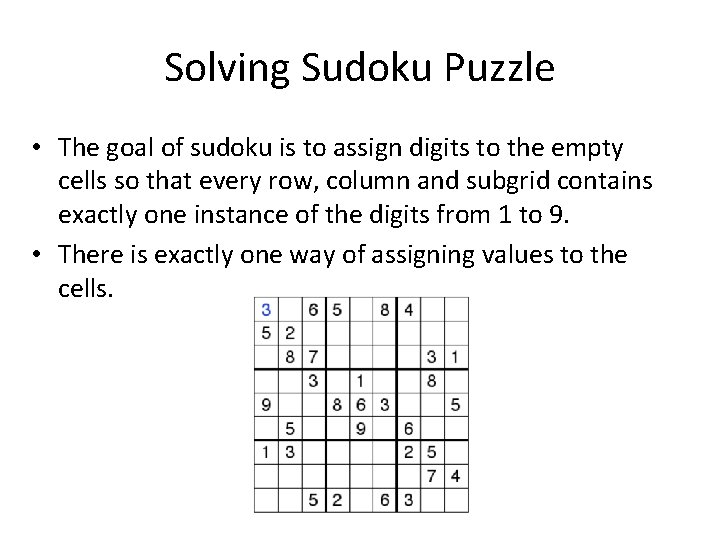
Solving Sudoku Puzzle • The goal of sudoku is to assign digits to the empty cells so that every row, column and subgrid contains exactly one instance of the digits from 1 to 9. • There is exactly one way of assigning values to the cells.

Pseudocode

Solve Sudoku

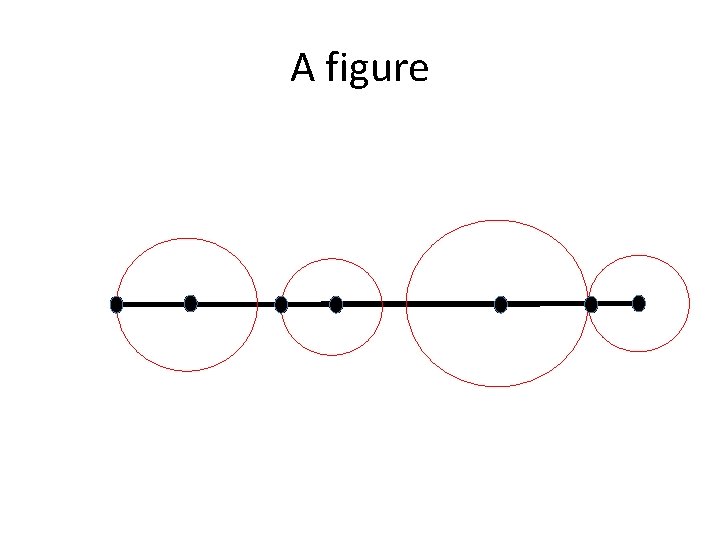
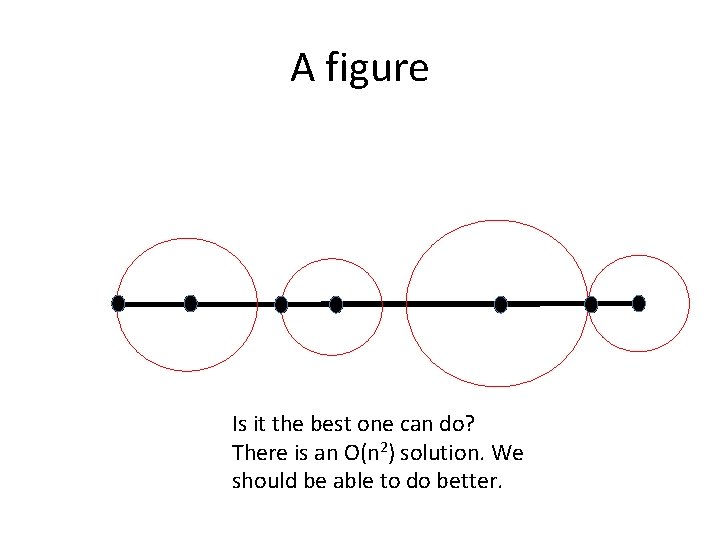
Maximum area discrete packing (MADP) • Given a set of points P = <p 1, p 2, …, pn> on a horizontal line L (sorted from left to right), compute the radii of a set of non-ovelappin discs C = {C 1, C 2, …, Cn}, where Ci is centered at pi of P such that area(C 1) + area(C 2) + …. . + area(Cn) is maximum.

Maximum area discrete packing (MADP) • The problem can be formulated as a quadratic programming problem maximize (r 12 + r 22 + …. +rn 2) subject to ri + rj ≤ dist(pi, pj), for all pi, pj in P, i≠j. • The problem is NP-hard if the points are distribute in the plane.

A figure

A figure Is it the best one can do? There is an O(n 2) solution. We should be able to do better.