Text Databases Text Types Unstructured text semistructured text

Text Databases · Text Types - · · · Unstructured text semi-structured text Query: User wants to find documents related to a topic T The search program tries to find the documents in the text database that contain the string T Two problems - Synonymy: Given a word T, the word T does not occur anywhere in a document D, even though D is in fact closely related to topic T Polysemy: The same word may mean many different things in different contexts 1

We discuss, · · · Measures of performance of a text retrieval system Latent semantic indexing Telescopic-Vector trees for document retrieval 2
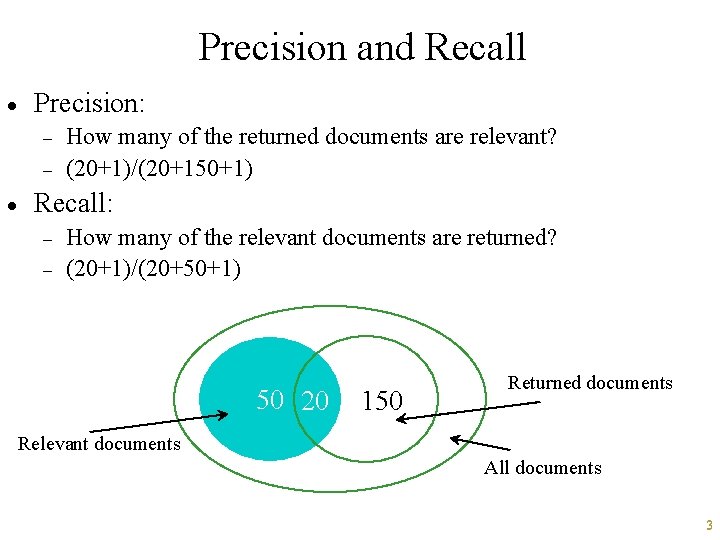
Precision and Recall · Precision: - · How many of the returned documents are relevant? (20+1)/(20+150+1) Recall: - How many of the relevant documents are returned? (20+1)/(20+50+1) 50 20 150 Returned documents Relevant documents All documents 3

Some Concepts · Stop List - · Word Stems - · · A set of words that do not “discriminate” between the documents in a given archive E. g. : Cornell SMART system has about 440 words on its stop list Many words are small syntactic variants of each other E. g. , drugged, drugs are similar in the sense that they share a common “stem, ” the word drug Most document retrieval systems first eliminate words on stop lists and reduce words to their stems, before creating a frequency table Frequency Tables 4

Some Concepts · Frequency Tables - D is a set of N documents T is a set of M words/terms occurring in the documents of D Assume no words on the stop list for D occur in T and all words in T have been stemmed The frequency table Freq. T is an (M N) matrix such that Freq. T(i, j) equals the number of occurrences of the word ti in the document dj Doc String Term/Doc d 1 d 2 d 3 d 4 drug boat iran connection 1 0 0 0 1 Sex, Drugs and Videotape The Iranian Connection Boating and Drugs: Slips owned by Cartel Connections between Terrorism and Asian Dope Operations 5

Similarity · · d 1 and d 2 are similar because the distribution of the words in d 1 mirrors the distribution of words in d 2 both contain lots of occurrences of t 1 and t 4 and relatively few occurrences of t 2 and t 3 and moderately many occurrences of t 5 d 3 and d 5 are also similar d 4 and d 6 stand out as sharply different Term/Doc t 1 t 2 t 3 t 4 t 5 d 1 d 2 d 3 615 390 10 15 4 76 2 8 815 312 511 677 45 33 516 d 4 d 5 d 6 10 217 142 11 64 65 816 1 2 59 18 91 765 711 491 6

Similarity · · · Is merely counting words enough? It does not indicate the importance of the words What about document lengths? We should also include the importance of the word in the document - How? If a word occurs 3 times in a 100 word document may have more significance than if it occurs 3 times in a million word document ratio of the number of occurrences of a word to the total number of words 7

Queries · User wants to execute the query - · · Find the 25 documents that are maximally relevant wrt banking operations and drugs? After stemming, relevant keywords are “drug, bank” Assume the query Q as vector We want to find the columns in Freq. T that are as close as possible to the Q’s vector Closeness Metrics - - Term Distance: (between Q and dr) = M j = 1 (vec. Q(j) - Freq. T(j, r))2 Cosine Distance: M j = 1 (vec. Q(j) Freq. T(j, r)) M j = 1 (vec. Q(j))2 M j = 1 (Freq. T(j, r))2 Complexity of retrievals may be O(N M) which could be very large (Latent Semantic Indexing- A solution!!!) 8

Latent Semantic Indexing · The number of documents M and the number of terms N is very large - · · · N could be over 10, 000 (English words, proper nouns) LSI tries to find a relatively small subset of K words which discriminate between M documents in the archive LSI is claimed to work effectively for around K = 200 Advantage: Each document is now a column vector of length 200, instead of length N (This is a big plus!!!) But, how do we find such a subset K? A technique called singular valued decomposition 9

LSI · 4 steps approach used by LSI - - Table creation: Creation of the frequency matrix Freq. T SVD Construction: Compute the singular valued decompositions (A, S, B) of Freq. T Vector Identification: For each document d, let vec(d) be the set of all terms in Freq. T whose corresponding rows have not been eliminated in the singular matrix S Index Creation: Store the set of all vec(d)’s indexed by any one of the number of techniques (such as TV-tree) 10

Singular Valued Decomposition · · Let M 1 and M 2 are two matrices of order (m 1 n 1) and (m 2 n 2), respectively M 1 M 2 is well defined iff n 1 = m 2 3 2 4 8 · 1 4 3 2 4 6 20 48 60 Transpose of M, MT T 7 20 21 20 48 60 = · = 7 20 21 7 20 20 48 21 60 Vector = matrix of order (1 m) 11

Singular Valued Decomposition · · Two vectors X and Y of the same order are said to be orthogonal iff XTY = 0 X = [10, 5, 20], Y = [1, 2, -1] 10 0 XTY = 5 [1 2 -1] = 0 20 0 · A Matrix M is orthogonal iff MT M is the identity matrix 1 M = 0 1 is orthogonal 0 12

Singular Valued Decomposition · Matrix M is said to be diagonal iff the order of M is (m m) and for all 1 i, j m, i j M(i, j) = 0 1 0 0 1 1 A= 0 4 0 ; B= 0 0 0 ; C= 0 0 5 0 0 0 · · · A and B are diagonal, but C is not A diagonal matrix M of order (m m) is said to be nondecreasing iff for all 1 i, j m, i j M(i, i) M(j, j) A is a non-decreasing diagonal matrix but B is not 13

SVD · A singular value decomposition of Freq. T is a triple (A, S, B) where: - · · 1. Freq. T = (A S BT) 2. A is an (M M) orthogonal matrix such that ATA = I 3. B is an (N N) orthogonal matrix such that BTB = I 4. S is a diagonal matrix called a singular matrix Theorem: Given any matrix M of order (m m), it is possible to find a singular value decomposition, (A, S, B) of M such that S is a non-decreasing diagonal matrix The SVD of the matrix 1. 44 0. 52 is given by: 0. 92 1. 44 . 6 -. 8 5 0 . 8. 6 0 2 . 8. 6 here the singular values are 5, 2. 6 -. 8 and the singular matrix S is non-decreasing 14

Returning to LSI · · · Given a frequency matrix Freq. T, we can decompose it into SVD TSDT where S is non-decreasing If Freq. T is of size (M N), then T is of size (M M) and S is of order (M R) where R is the rank of Freq. T, and DT is of the order (R N) We can now shrink the problem substantially by eliminating the least significant singular values from the singular matrix S - Choose an integer k that is substantially smaller than R Replace S by S*, which is a (k k) matrix such that S*(i, j) = S(i, j) for 1 i, j k Replace the (R N) matrix DT by the (k N) matrix D*T where D*T(i, j) = DT(i, j) if 1 i k and 1 j N 15

LSI · How? 20 0 16 0 0 0 12 0 0. 08 0 0 0 · 0 0 0 0. 004 20 0 16 0 0 0 12 Bottom line: - Throw away the least significant values and retain the rest of the matrix Key claim in LSI is that if k is chosen judiciously, then the k rows appearing in the singular matrix S* represent the k “most important” (from the point of view of retrieval) terms occurring in the “entire” document 16

Analysis · · Usually R is taken to be 200 The size of Freq. T is (M N), - · After shrinking the singular matrix to 200 - · · where M = number of terms = 1, 000 N = number of documents = 10, 000 (even for a small database) the first matrix: (M R) = 1, 000 200 = 200, 000 the singular matrix: (R R) = 200 = 400, 000 (only 200 need to be stored because all others are 0’s) the last matrix: (R N) = 200 10, 000 A total of 202, 000, 200 (200 million) In contrast, (M N) is close to 10, 000 million!!! SVD reduced the space utilized to about 1/50 th of that required by the original frequency table 17

LSI: Document Retrieval using SVD · · · Given 2 documents d 1 and d 2 in the archive, how similar are they? Given a query string/document Q, what are the n documents in the archive that are most relevant for the query? Dot Product - · Suppose x = (x 1, … xw) and y = (y 1, …, yw) The dot product of x and y = xi yi (where i = 1, . . w) Similarity of these two documents wrt the SVD representation TS* D*T of a freq table is the dot product of the two columns in the matrix D*T of the two documents 18

LSI: Document Retrieval using SVD · The top p matches for Q - · · · 1. For all 1 i j p, the similarity between vec. Q and di is greater than or equal to the similarity between vec. Q and dj 2. There is no other document dz such that the similarity between dz and vec. Q exceeds that of dp Can be done by using any indexing structure for Rdimensional spaces (R-trees, k-d trees) However R-trees, k-d trees do not work well for highdimensional data (>20) Solution: TV-trees! 19

Telescopic Vector (TV) Trees · · · Access to point data in very large dimensional spaces should be highly efficient A document d may be viewed as a vector v of length k, where the singular matrix is of size (k k) Thus each document is a point in a k-dimensional space A document database is a collection of such points To find the top p matches for Q, expressed as vec. Q of length k, we need to find the k-nearest neighbors vec. Q TV-tree is a data structure similar to R-trees 20

Organization of a TV-tree · · · Num. Child: Max number of a node is allowed to have : is a number, > 0, < k is the number of active dimensions Each in TV(k, Num. Child, ) represents a region, for this purpose, each node contains 3 fields - N. Center: this is a point in k-dimensional space N. Radius: A real number > 0 N. Active. Dims: A list of at most dimensions, It is a subset of {1, …k} of cardinality or less 21

Region associated with a node N · Suppose x and y are points in k-dim space - · Let k = 200, = 5 and the set of Active. Dims = {1, 2, 3, 4, 5} - · x = (10, 5, 11, 13, 7, x 6, …. x 200) y = (2, 4, 14, 8, 6, y 6, …y 200) act-dist(x, y) = (10 -2)2 + (5 -4)2 + (11 -14)2 + (13 -8)2 + (7 -6)2 = 10 Node N represents the region containing all points x such that the active distance between x and N. Center N. Radius - · act-dist(x, y) = (xi - yi)2 where i Active. Dims if N. Center = (10, 5, 11, 13, 7, 0, 0, 0… 0) N. Active. Dims = {1, 2, 3, 4, 5} then N represents the region consisting of all points x such that (x 1 -10)2 + (x 2 -5)2 + (x 3 -14)2 + (x 4 -13)2 + (x 5 -7)2 N. Radius A node also contains an array, Child, of pointers to other nodes 22

Properties of TV- Trees · · · All data is stored at the leaf nodes Each node (except the root and the leaves) must be at least half full If N is a node, and N 1, . . Nr are its children, then - Region(N) is Union of all Region(Ni)’s 23

Insertion into TV-trees · · Three steps: 1. Branch Selection: When we insert a new vector v at node N, - - · for each child Nj of N, compute exp(v) = the amount we must expand Nj. Radius so that v’s active distance from Nj. Center falls within this region select a branch such that exp(v) is minimum 2. Splitting: When a leaf node is full and cannot accommodate the new vector v, we have to split. - - Split vectors into 2 groups G 1, H 1 such that we enclose all vectors in G 1 with center c 1 and radius r 1, and all in H 1 with center c 1’ and r 1’ There exist many such cases: G 2, H 2 (with (c 2, r 2), (c 2’, r 2’) take the one with minimum sum of radii, i. e. , G 1, H 1 is better if (r 1+r 1’) < (r 2+r 2’) 24

Insertion into TV-trees · 3. Telescoping: The active dimensions associated with a node or the children of the node change (either expand or contract); this is called telescoping. This happens in 2 cases: - - When a node splits into two subnodes N 1 and N 2, vectors in region(N 1) all agree on not just the active dimensions of N, but a few more as well When a new vector is added to a node N, the active dimensions may reduce 25

· Other Retrieval Techniques: Inverted Indices A document_record contains 2 fields: doc_id, postings_list - · A term_record consists of 2 fields: term, postings_list - · postings_list is list specifying which documents the term appeared in Two hash tables are maintained: Doc. Table, Term. Table - · postings_list is a list of terms (or pointers to terms) that occur in the document. Sorted using a suitable relevance measure Doc. Table is constructed by hashing on doc_id Term. Table by hashing on term To find all documents associated with a term, merely return the postings_list 26

· · · Other Retrieval Techniques: Signature Files Associate a signature with each document signature: is a representation of an ordered list of terms that describe the document the list of terms in the signature may be derived from a frequency analysis, stemming, usage of stop lists 27
- Slides: 27