CMPUT 680 Winter 2006 Topic G Static Single

CMPUT 680 - Winter 2006 Topic G: Static Single. Assignment Form José Nelson Amaral http: //www. cs. ualberta. ca/~amaral/courses/680 CMPUT 680 - Compiler Design and Optimization 1

Reading Material Chapter 19 of the “Tiger book” (with a grain of salt!!). Bilardi, G. , Pingali, K. , “The Static Single Assignment Form and its Computation, ” unpublished? (citeseer). Cytron, R. , Ferrante, J. , Rosen, B. K. , Wegman, M. N. , Zadeck, F. K. , “An Efficient Method of Computing Static Single Assignment Form, ” ACM Symposium on Principles of Programming Languages (Po. PL), pp. 25 -35, Austin, TX, Jan. , 1989. Cytron, R. , Ferrante, J. , Rosen, B. K. , Wegman, M. N. , “Efficiently Computing Static Single Assignment Form and the Control Dependence Graph, ” ACM Transactions on Programming Languages and Systems (TOPLAS), Vol. 13, No. 4, October, 1991, pp. 451 -490. Sreedhar, V. C. , Gao, G. R. , “A Linear Time Algorithm for Placing -Nodes, ” ACM Symposium on Principles of Programming Languages (Po. PL), pp. 62 -73, 1995. CMPUT 680 - Compiler Design and Optimization 2

Static Single-Assignment Form Each variable has only one definition in the program text. This single static definition can be in a loop and may be executed many times. Thus even in a program expressed in SSA, a variable can be dynamically defined many times. CMPUT 680 - Compiler Design and Optimization 3

Advantages of SSA Simpler dataflow analysis No need to use-def/def-use chains, which requires N M space for N uses and M definitions SSA form relates in a useful way with dominance structures. SSA simplifies algorithms that construct interference graphs. CMPUT 680 - Compiler Design and Optimization 4

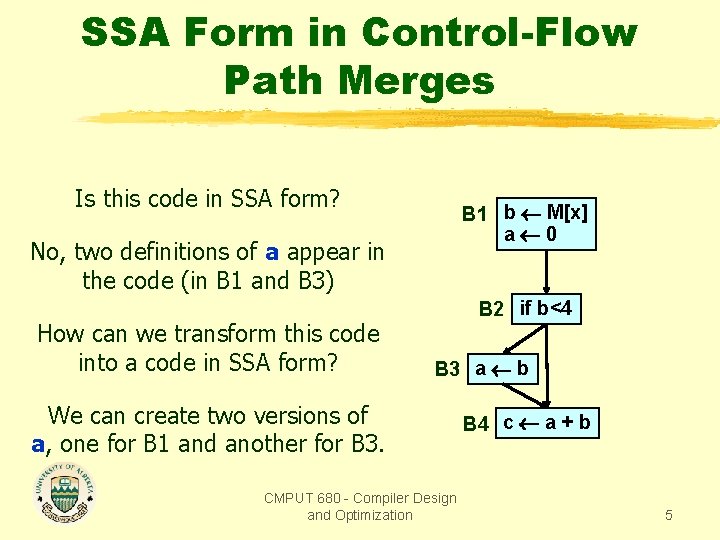
SSA Form in Control-Flow Path Merges Is this code in SSA form? B 1 b M[x] a 0 No, two definitions of a appear in the code (in B 1 and B 3) How can we transform this code into a code in SSA form? B 2 if b<4 B 3 a b We can create two versions of a, one for B 1 and another for B 3. CMPUT 680 - Compiler Design and Optimization B 4 c a + b 5

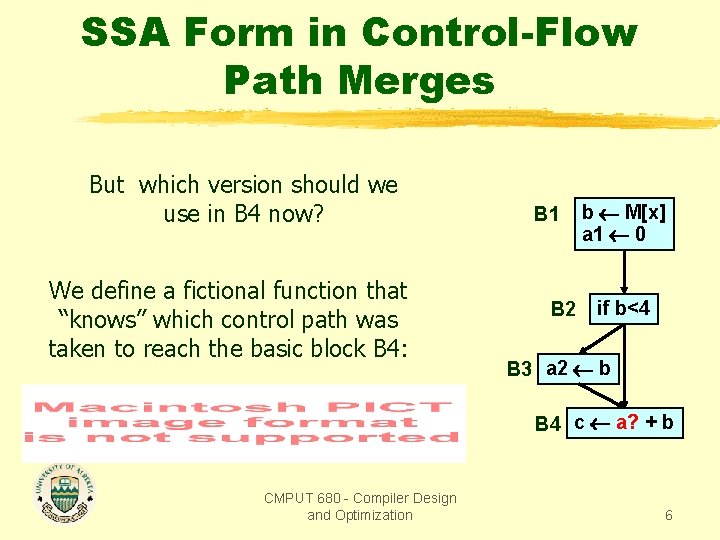
SSA Form in Control-Flow Path Merges But which version should we use in B 4 now? We define a fictional function that “knows” which control path was taken to reach the basic block B 4: B 1 B 2 b M[x] a 1 0 if b<4 B 3 a 2 b B 4 c a? + b CMPUT 680 - Compiler Design and Optimization 6

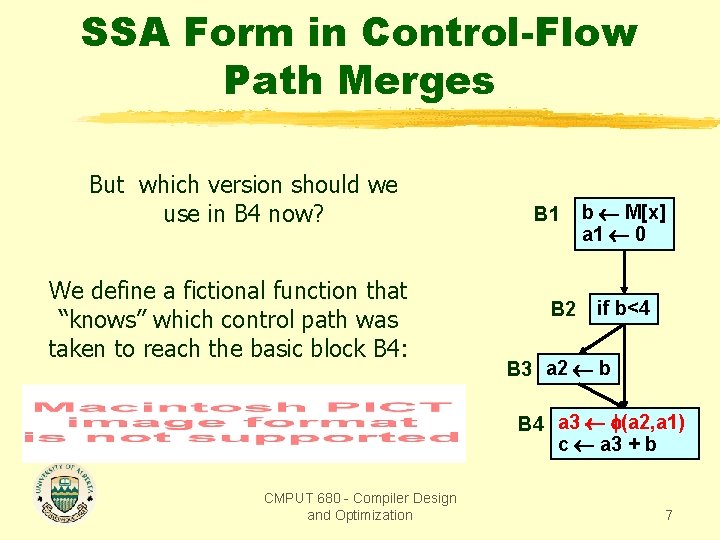
SSA Form in Control-Flow Path Merges But which version should we use in B 4 now? We define a fictional function that “knows” which control path was taken to reach the basic block B 4: B 1 B 2 b M[x] a 1 0 if b<4 B 3 a 2 b B 4 a 3 (a 2, a 1) c a 3 + b CMPUT 680 - Compiler Design and Optimization 7

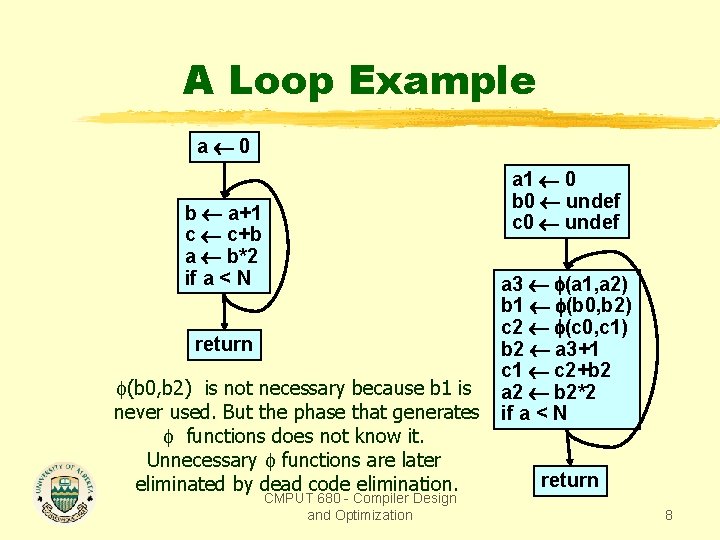
A Loop Example a 0 a 1 0 b 0 undef c 0 undef b a+1 c c+b a b*2 if a < N return (b 0, b 2) is not necessary because b 1 is never used. But the phase that generates functions does not know it. Unnecessary functions are later eliminated by dead code elimination. CMPUT 680 - Compiler Design and Optimization a 3 (a 1, a 2) b 1 (b 0, b 2) c 2 (c 0, c 1) b 2 a 3+1 c 1 c 2+b 2 a 2 b 2*2 if a < N return 8

The Function How can we implement a function that “knows” which control path was taken? Answer 1: We don’t!! The function is used only to connect use to definitions during optimization, but is never implemented. Answer 2: If we must execute the function, we can implement it by inserting MOVE instructions in all control paths. CMPUT 680 - Compiler Design and Optimization 9

Criteria for Inserting Functions We could insert one function for each variable at every join point (a point in the CFG with more than one predecessor). But that would be wasteful. What criteria should we use to insert a function for a variable a at node z of the CFG? Intuitively, we should add a function if there are two definitions of a that can reach the point z through distinct paths. CMPUT 680 - Compiler Design and Optimization 10

Path Convergence Criterion (Cytron-Ferrante/89) Insert a function for a variable a at a node z if all the following conditions are true: 1. There is a block x that defines a 2. There is a block y x that defines a 3. There is a non-empty paths x z and y z 4. Paths x z and y z don’t have any nodes in common other than z 5. The node z does not appear within both x z and y z prior to the end, but it may appear in one or the other. Note: The start node contains an implicit definition of every CMPUT 680 - Compiler Design variable. and Optimization 11

-Candidates are Join Nodes Notice that according to the path convergence criterion, the node z that will receive the function must be a join node. z is the first node that joins the paths Pxz and Pyz. CMPUT 680 - Compiler Design and Optimization 12

Iterated Path-Convergence Criterion The function itself is a definition of a. Therefore the path-convergence criterion is a set of equations that must be satisfied. while there are nodes x, y, z satisfying conditions 1 -5 and z does not contain a function for a do insert a (a 0, a 1, …, an) at node z This algorithm is extremely costly, because it requires the examination of every triple of nodes x, y, z and every path from x to z and from y to z. Can better? CMPUTwe 680 do - Compiler Design and Optimization 13

The SSA Conversion Problem For each variable x defined in a CFG G=(V, E), given the set of nodes S V that contain a definition for x, find the minimal set, J(S) of nodes that requires a (xi, xj) function. By definition, the START node defines all the variables, therefore S V, START S. If we need to compute nodes for several variables, it may be efficient to precompute data structures based on the CFG. CMPUT 680 - Compiler Design and Optimization 14

Processing Time for SSA Conversion The performance of an SSA conversion algorithm should be measured by the processing time Tp, the preprocessing space Sp, and the query time Tq. (Shapiro and Saint 1970): outline an algorithm (Reif and Tarjan 1981): extend the Lengauer-Tarjan dominator algorithm to compute -nodes. (Cytron et al. 1991): show that SSA conversion can use the idea of dominance frontiers, resulting on an O(|V|2) algorithm. (Sreedhar and Gao, 1995): An O(|E|) algorithm, but in private commun. with Pingali in 1996 admits that it is in practice 5 times slower than Cytron et al. CMPUT 680 - Compiler Design and Optimization 15

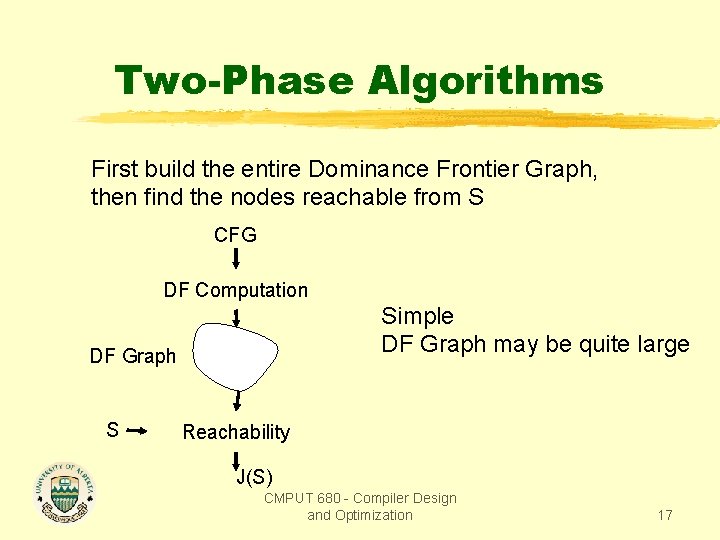
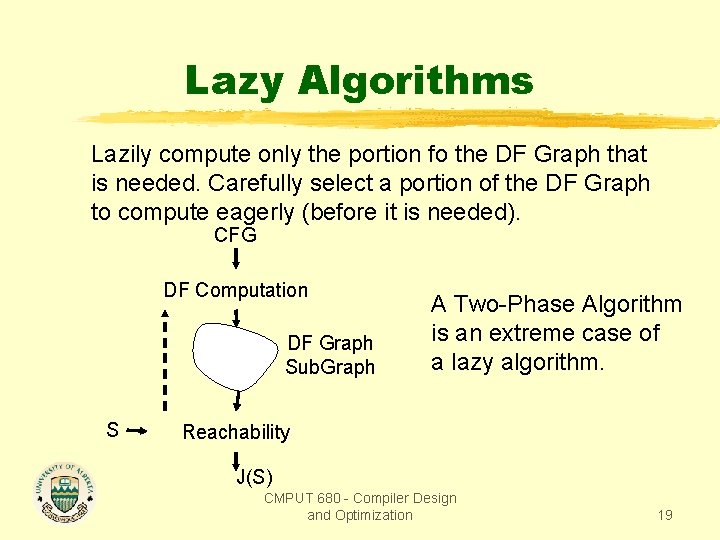
Processing Time for SSA Conversion Bilardi, Pingali, 1999: present a generalized framework and a parameterized Augmented Dominator Tree (ADT) algorithm that allows for a space-time tradeoff. They show that Cytron et al. and Gao-Shreedhar are special cases of the ADT algorithm. Bilardi and Pingali describe three strategies to compute -placement: • Two-Phase Algorithms • Lock-Step Algorithms • Lazy Algorithms CMPUT 680 - Compiler Design and Optimization 16

Two-Phase Algorithms First build the entire Dominance Frontier Graph, then find the nodes reachable from S CFG DF Computation Simple DF Graph may be quite large DF Graph S Reachability J(S) CMPUT 680 - Compiler Design and Optimization 17

Lock-Step Algorithms Performs the reachability computation incrementally while the DF relation is computed. CFG S DF Computation Reachability J(S) • Avoid storing the DF Graph. • Perform computations at all nodes of the graph, even though most are irrelevant • Inneficient when computing the -nodes for many variables. CMPUT 680 - Compiler Design and Optimization 18

Lazy Algorithms Lazily compute only the portion fo the DF Graph that is needed. Carefully select a portion of the DF Graph to compute eagerly (before it is needed). CFG DF Computation DF Graph Sub. Graph S A Two-Phase Algorithm is an extreme case of a lazy algorithm. Reachability J(S) CMPUT 680 - Compiler Design and Optimization 19

Computing a Dominator Tree (n: # of nodes; m: # of edges) (Lowry and Medlock, 1969): Introduce the problem and give an O(n 4) algorithm. (Lengauer and Tarjan, 1979): Give a complicated O(m (m. n)) algorithm [ (m. n) is the inverse Ackermann’s function]. (Harel, 1985): Give a linear time algorithm. (Alstrup, Harel and Thorup, 1997): Give a simpler version of Harel’s algorithm. CMPUT 680 - Compiler Design and Optimization 20

Dominance Property of the SSA Form In SSA form definitions dominate uses, i. e. : 1. If x is used in a function in block n, then the definition of x dominates every predecessor of n. 2. If x is used in a non- statement in block n, then the definition of x dominates n. CMPUT 680 - Compiler Design and Optimization 21

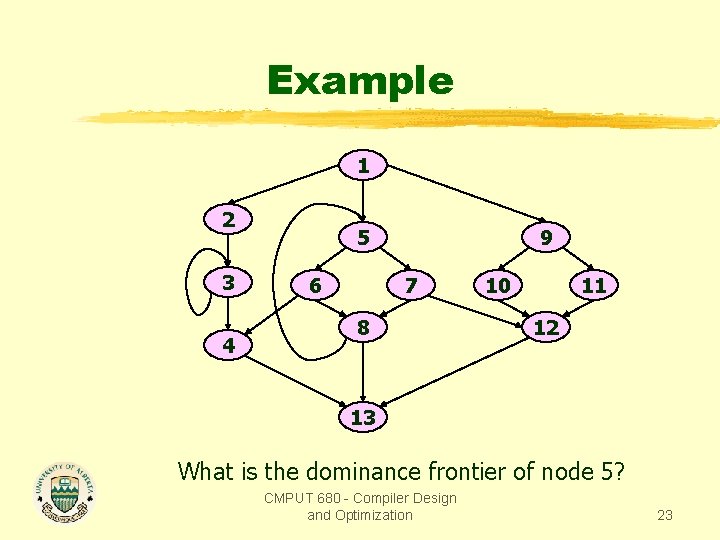
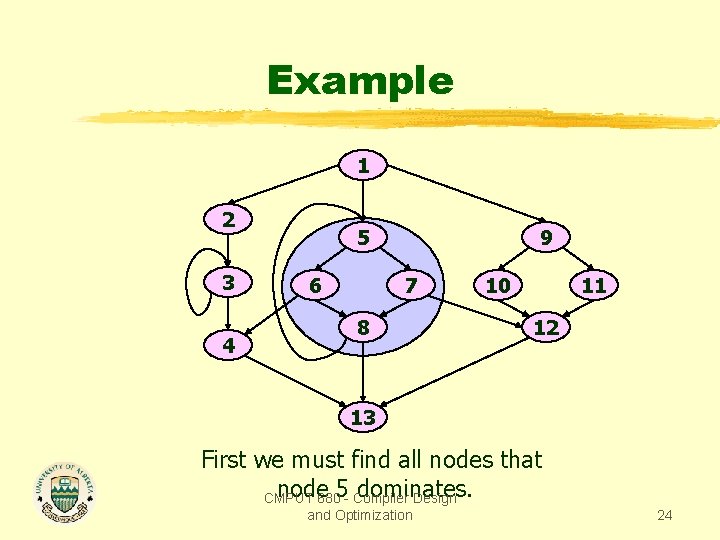
The Dominance Frontier A node x dominates a node w if every path from the start node to w must go through x. A node x strictly dominates a node w if x dominates w and x w. The dominance frontier of a node x is the set of all nodes w such that x dominates a predecessor of w, but x does not strictly dominates w. CMPUT 680 - Compiler Design and Optimization 22

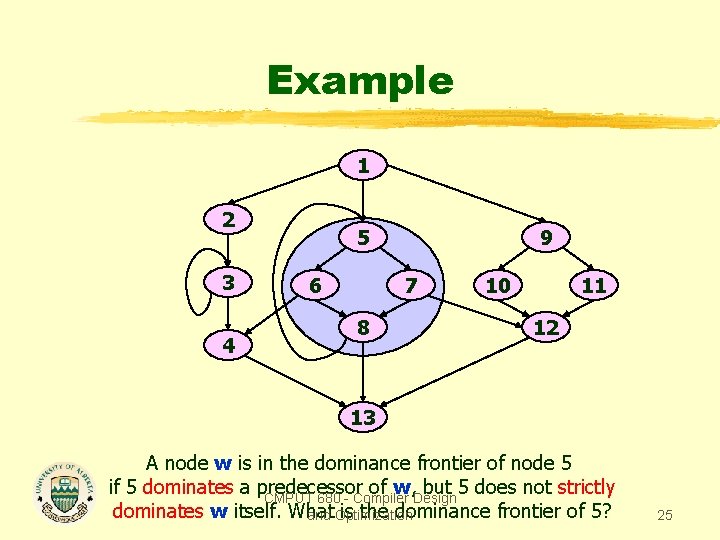
Example 1 2 3 4 5 6 9 7 8 10 11 12 13 What is the dominance frontier of node 5? CMPUT 680 - Compiler Design and Optimization 23

Example 1 2 3 4 5 6 9 7 8 10 11 12 13 First we must find all nodes that node 6805 - Compiler dominates. CMPUT Design and Optimization 24

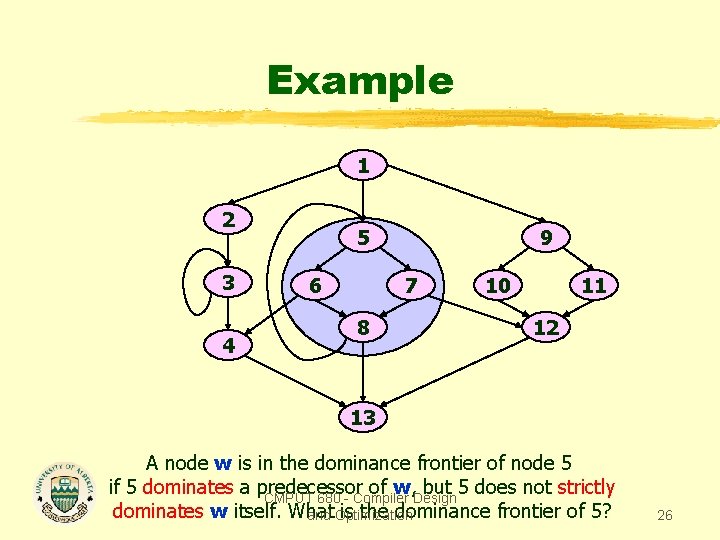
Example 1 2 3 4 5 6 9 7 8 10 11 12 13 A node w is in the dominance frontier of node 5 if 5 dominates a predecessor of w, but 5 does not strictly CMPUT 680 - Compiler Design dominates w itself. What is the dominance frontier of 5? and Optimization 25

Example 1 2 3 4 5 6 9 7 8 10 11 12 13 A node w is in the dominance frontier of node 5 if 5 dominates a predecessor of w, but 5 does not strictly CMPUT 680 - Compiler Design dominates w itself. What is the dominance frontier of 5? and Optimization 26

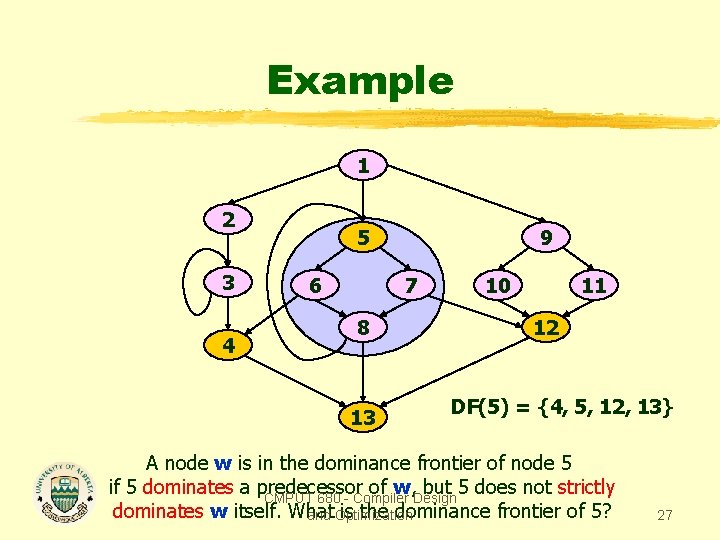
Example 1 2 3 4 5 6 9 7 8 13 10 11 12 DF(5) = {4, 5, 12, 13} A node w is in the dominance frontier of node 5 if 5 dominates a predecessor of w, but 5 does not strictly CMPUT 680 - Compiler Design dominates w itself. What is the dominance frontier of 5? and Optimization 27

Dominance Frontier Criterion: If a node x contains a definition of variable a, then any node z in the dominance frontier of x needs a function for a. Can you think of an intuitive explanation for why a node in the dominance frontier of another node must be a join node? CMPUT 680 - Compiler Design and Optimization 28

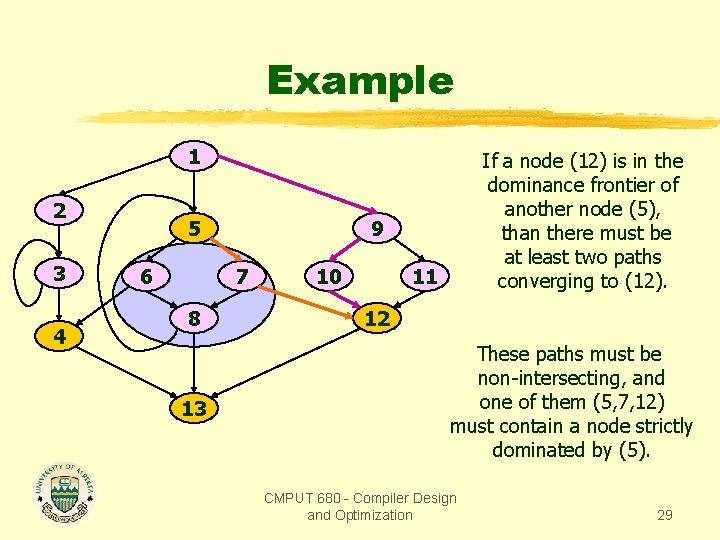
Example 1 2 3 4 5 6 9 7 8 13 If a node (12) is in the dominance frontier of another node (5), than there must be at least two paths converging to (12). 10 11 12 These paths must be non-intersecting, and one of them (5, 7, 12) must contain a node strictly dominated by (5). CMPUT 680 - Compiler Design and Optimization 29

Dominator Tree To compute the dominance frontiers, we first compute the dominator tree of the CFG. There is an edge from node x to node y in the dominator tree if node x immediately dominates node y. I. e. , x dominates y x, and x does not dominate any other dominator of y. Dominator trees can be computed using the Lengauer-Tarjan algorithm(1979). See sec. 19. 2 of Appel. CMPUT 680 - Compiler Design and Optimization 30

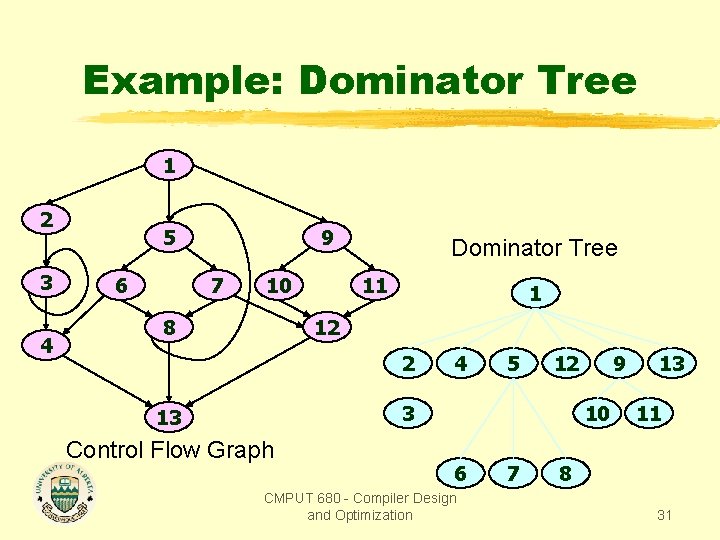
Example: Dominator Tree 1 2 3 4 5 6 9 7 10 8 Dominator Tree 11 1 12 2 4 5 12 3 13 Control Flow Graph 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 31

Local Dominance Frontier Cytron-Ferrante define the local dominance frontier of a node n as: DFlocal[n] = successors of n in the CFG that are not strictly dominated by n CMPUT 680 - Compiler Design and Optimization 32

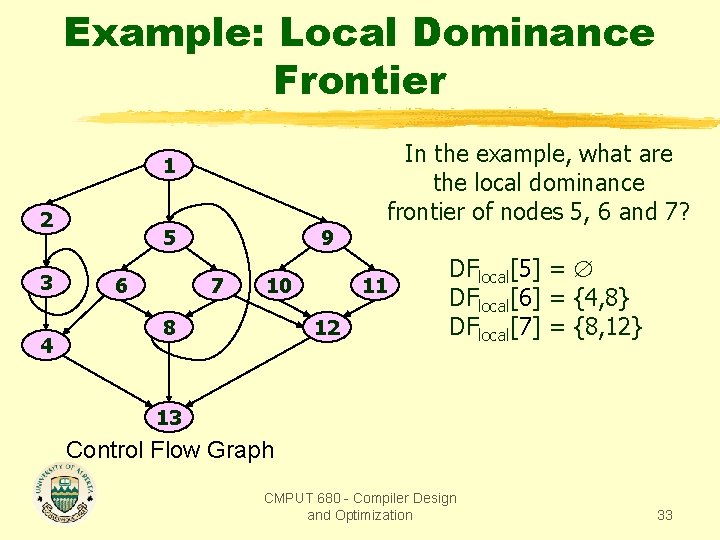
Example: Local Dominance Frontier In the example, what are the local dominance frontier of nodes 5, 6 and 7? 1 2 3 4 5 6 9 7 10 8 11 12 DFlocal[5] = DFlocal[6] = {4, 8} DFlocal[7] = {8, 12} 13 Control Flow Graph CMPUT 680 - Compiler Design and Optimization 33

Dominance Frontier Inherited From Its Children The dominance frontier of a node n is formed by its local dominance frontier plus nodes that are passed up by the children of n in the dominator tree. The contribution of a node c to its parents dominance frontier is defined as [Cytron-Ferrante, 1991]: DFup[c] = nodes in the dominance frontier of c that are not strictly dominated by the immediate dominator of c CMPUT 680 - Compiler Design and Optimization 34

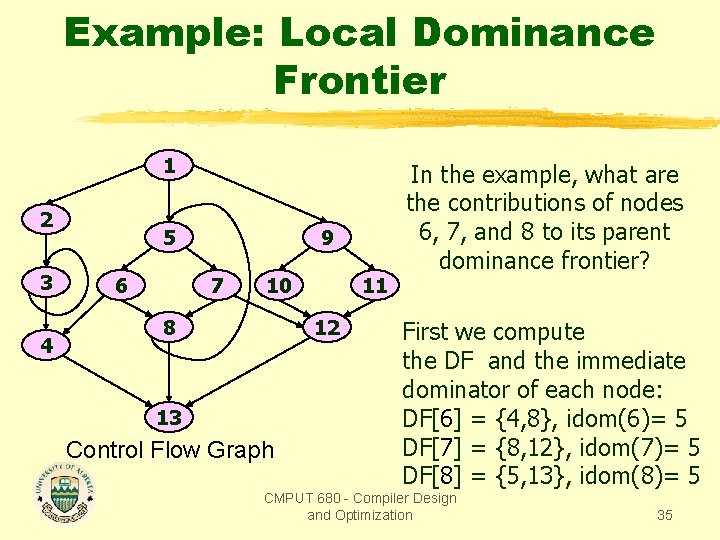
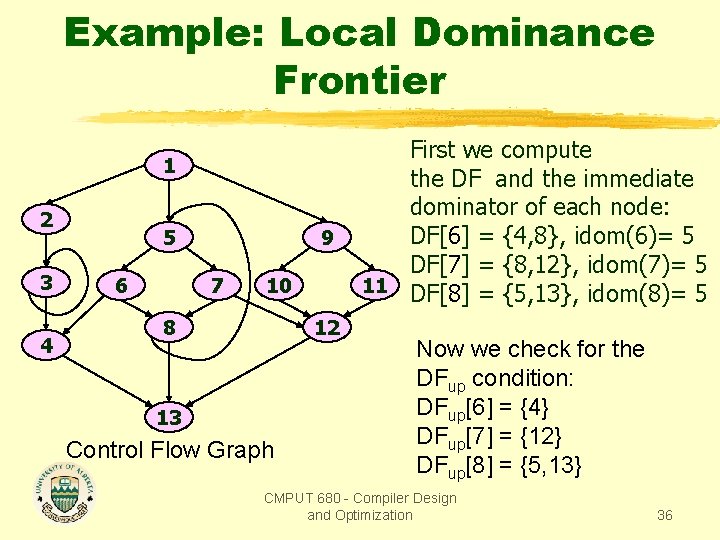
Example: Local Dominance Frontier 1 2 3 4 5 6 9 7 10 8 11 12 13 Control Flow Graph In the example, what are the contributions of nodes 6, 7, and 8 to its parent dominance frontier? First we compute the DF and the immediate dominator of each node: DF[6] = {4, 8}, idom(6)= 5 DF[7] = {8, 12}, idom(7)= 5 DF[8] = {5, 13}, idom(8)= 5 CMPUT 680 - Compiler Design and Optimization 35

Example: Local Dominance Frontier 1 2 3 4 5 6 9 7 10 8 12 13 Control Flow Graph First we compute the DF and the immediate dominator of each node: DF[6] = {4, 8}, idom(6)= 5 DF[7] = {8, 12}, idom(7)= 5 11 DF[8] = {5, 13}, idom(8)= 5 Now we check for the DFup condition: DFup[6] = {4} DFup[7] = {12} DFup[8] = {5, 13} CMPUT 680 - Compiler Design and Optimization 36

A note on implementation We want to represent these sets efficiently: DF[6] = {4, 8} DF[7] = {8, 12} DF[8] = {5, 13} If we use bitvectors to represent these sets: DF[6] = 0000 0001 0000 DF[7] = 0001 0000 DF[8] = 0010 0000 CMPUT 680 - Compiler Design and Optimization 37

Strictly Dominated Sets We can also represent the strictly dominated sets as vectors: SD[1] = 0011 1111 1100 SD[2] = 0000 1000 SD[5] = 0000 0001 1100 0000 Dominator Tree SD[9] = 0000 1100 0000 1 2 4 5 12 3 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 38

A note on implementation If we use bitvectors to represent these sets: DF[6] = 0000 0001 0000 DF[7] = 0001 0000 DF[8] = 0010 0000 SD[5] = 0000 0001 1100 0000 DFup[c] = DF[6] ^ ~SD[5] DFup[c] = nodes in the dominance frontier of c. CMPUT that 680 are not strictly dominated by - Compiler Design and Optimization the immediate dominator of c 39

Dominance Frontier Inherited From Its Children The dominance frontier of a node n is formed by its local dominance frontier plus nodes that are passed up by the children of n in the dominator tree. Thus the dominance frontier of a node n is defined as [Cytron-Ferrante, 1991]: CMPUT 680 - Compiler Design and Optimization 40

Example: Local Dominance Frontier 1 2 3 4 What is DF[5]? 5 6 Remember that: 9 7 10 8 11 12 DFlocal[5] = DFup[6] = {4} DFup[7] = {12} DFup[8] = {5, 13} DTchildren[5] = {6, 7, 8} 13 Control Flow Graph CMPUT 680 - Compiler Design and Optimization 41

Example: Local Dominance Frontier 1 2 3 4 What is DF[5]? 5 6 Remember that: 9 7 10 8 11 12 DFlocal[5] = DFup[6] = {4} DFup[7] = {12} DFup[8] = {5, 13} DTchildren[5] = {6, 7, 8} 13 Control Flow Graph Thus, DF[5] = {4, 5, 12, 13} CMPUT 680 - Compiler Design and Optimization 42

Join Sets In order to insert -nodes for a variable x that is defined in a set of nodes S={n 1, n 2, …, nk} we need to compute the iterated set of join nodes of S. Given a set of nodes S of a control flow graph G, the set of join nodes of S, J(S), is defined as follows: J(S) ={z G| two paths Pxz and Pyz in G that have z as its first common node, x S and y S} CMPUT 680 - Compiler Design and Optimization 43

Iterated Join Sets Because a -node is itself a definition of a variable, once we insert -nodes in the join set of S, we need to find out the join set of S J(S). Thus, Cytron-Ferrante define the iterated join set of a set of nodes S, J+(S), as the limit of the sequence: CMPUT 680 - Compiler Design and Optimization 44

Iterated Dominance Frontier We can extend the concept of dominance frontier to define the dominance frontier of a set of nodes as: Now we can define the iterated dominance frontier, DF+(S), of a set of nodes S as the limit of the sequence: Exercise: Find an example in which CMPUT 680 - Compiler Design and Optimization the IDF of a set S is different 45 from the DF of the set!

Location of -Nodes Given a variable x that is defined in a set of nodes S={n 1, n 2, …, nk} the set of nodes that must receive -nodes for x is J+(S). An important result proved by Cytron-Ferrante is that: Thus we are mostly interested in computing the iterated dominance frontier of a set of nodes. CMPUT 680 - Compiler Design and Optimization 46

Algorithms to Compute Dominance Frontier The algorithm to insert -nodes, due to Cytron and Ferrante (1991), computes the dominance frontier of each node in the set S before computing the iterated dominance frontier of the set. In the worst case, the combination of the dominance frontier of the sets can be quadratic in the number of nodes in the CFG. Thus, Cytron-Ferrante’s algorithm has a complexity O(N 2). In 1994, Shreedar and Gao proposed a simple, linear algorithm for the insertion of -nodes. CMPUT 680 - Compiler Design and Optimization 47

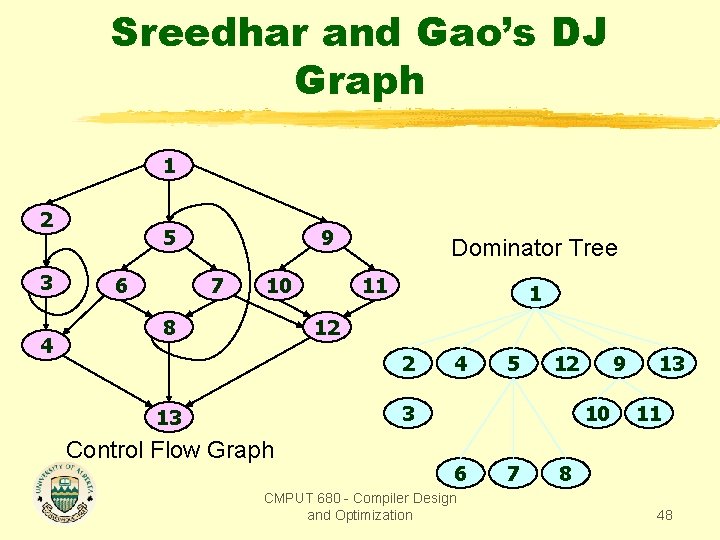
Sreedhar and Gao’s DJ Graph 1 2 3 4 5 6 9 7 10 8 Dominator Tree 11 1 12 2 4 5 12 3 13 Control Flow Graph 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 48

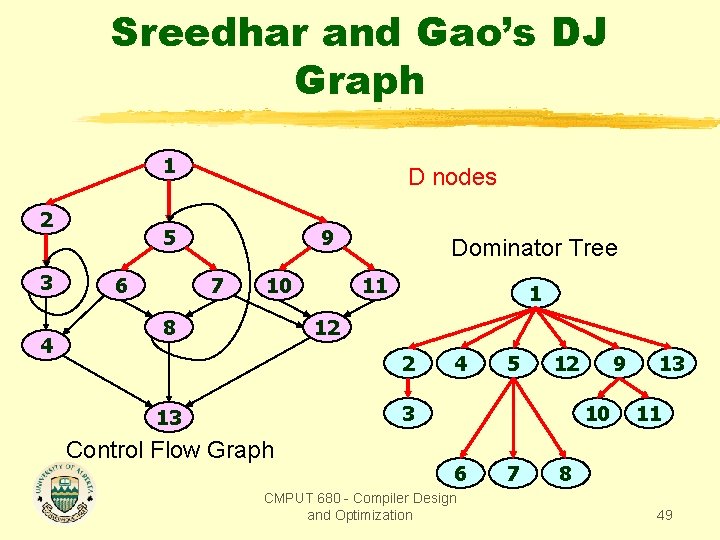
Sreedhar and Gao’s DJ Graph 1 2 3 4 D nodes 5 6 9 7 10 8 Dominator Tree 11 1 12 2 4 5 12 3 13 Control Flow Graph 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 49

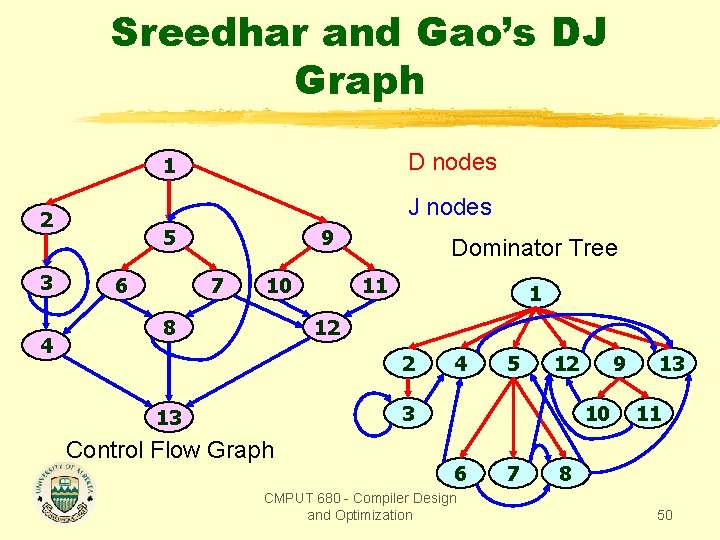
Sreedhar and Gao’s DJ Graph D nodes 1 J nodes 2 3 4 5 6 9 7 10 8 Dominator Tree 11 1 12 2 4 5 12 3 13 Control Flow Graph 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 50

Shreedar-Gao’s Dominance Frontier Algorithm Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z 1 2 What is the DF[5]? 4 5 12 3 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 51

Shreedar-Gao’s Dominance Frontier Algorithm Initialization: DF[5] = Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z Sub. Tree(5) = {5, 6, 7, 8} 1 2 4 5 12 3 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 52

Shreedar-Gao’s Dominance Frontier Algorithm Initialization: DF[5] = Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z 1 Sub. Tree(5) = {5, 6, 7, 8} 2 There are three edges originating in 5: {5 6, 5 7, 5 8} but they are all D-edges 3 4 5 12 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 53

Shreedar-Gao’s Dominance Frontier Algorithm Initialization: DF[5] = After visiting 6: DF = {4} Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z 1 Sub. Tree(5) = {5, 6, 7, 8} 2 There are two edges originating in 6: {6 4, 6 8} but 8. level > 5. level 3 4 5 12 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 54

Shreedar-Gao’s Dominance Frontier Algorithm Initialization: DF[5] = After visiting 6: DF = {4} After visiting 7: DF = {4, 12} Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z 1 Sub. Tree(5) = {5, 6, 7, 8} 2 There are two edges originating in 7: {7 8, 7 12} again 8. level > 5. level 3 4 5 12 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 55

Shreedar-Gao’s Dominance Frontier Algorithm Dominance. Frontier(x) 0: DF[x] = 1: foreach y Sub. Tree(x) do 2: if((y z == J-edge) and 3: (z. level x. level)) 4: then DF[x] = DF[x] z Initialization: DF[5] = After visiting 6: DF = {4} After visiting 7: DF = {4, 12} After visiting 8: DF = {4, 12, 5, 13} 1 Sub. Tree(5) = {5, 6, 7, 8} 2 There are two edges originating in 8: {8 5, 8 13} both satisfy cond. in steps 2 -3 3 4 5 12 9 10 6 CMPUT 680 - Compiler Design and Optimization 7 13 11 8 56

Shreedhar-Gao’s -Node Insertion Algorithm Using the D-J graph, Shreedhar and Gao propose a linear time algorithm to compute the iterated dominance frontier of a set of nodes. An important intuition in Shreedhar-Gao’s algorithm is: If two nodes x and y are in S, and y is an ancestor of x in the dominator tree, then if we compute DF[x] first, we do not need to recompute DF[x] when computing DF[y]. CMPUT 680 - Compiler Design and Optimization 57

Shreedhar-Gao’s -Node Insertion Algorithm Shreedhar-Gao’s algorithm also use a work list of nodes hashed by their level in the dominator tree and a visited flag to avoid visiting the same node more than once. The basic operation of the algorithm is similar to their dominance-frontier algorithm, but it requires a careful implementation to deliver the linear-time complexity. CMPUT 680 - Compiler Design and Optimization 58

Dead-Code Elimination in SSA Form Because there is only one definition for each variable, if the list of uses of the variable is empty, the definition is dead. When a statement v x y is eliminated because v is dead, this statement must be removed from the list of uses of x and y. Which might cause those definitions to become dead. Thus we need to iterate the dead code elimination algorithm. CMPUT 680 - Compiler Design and Optimization 59

Simple Constant Propagation in SSA If there is a statement v c, where c is a constant, then all uses of v can be replaced for c. A function of the form v (c 1, c 2, …, cn) where all ci are identical can be replaced for v c. Using a work-list algorithm in a program in SSA form, we can perform constant propagation in linear time In the next slide we assume that x, y, z are variables and a, b, c are constants. CMPUT 680 - Compiler Design and Optimization 60

Linear Time Optimizations in SSA form Copy propagation: The statement x (y) or the statement x y can be deleted and y can substitute every use of x. Constant folding: If we have the statement x a b, we can evaluate c a b at compile time and replace the statement for x c Constant conditions: The conditional if a < b goto L 1 else L 2 can be replaced for goto L 1 or goto L 2, according to the compile time evaluation of a < b, and the CFG, use lists, adjust accordingly CMPUT 680 - Compiler Design Unreachable Code: eliminate unreachable blocks. and Optimization 61

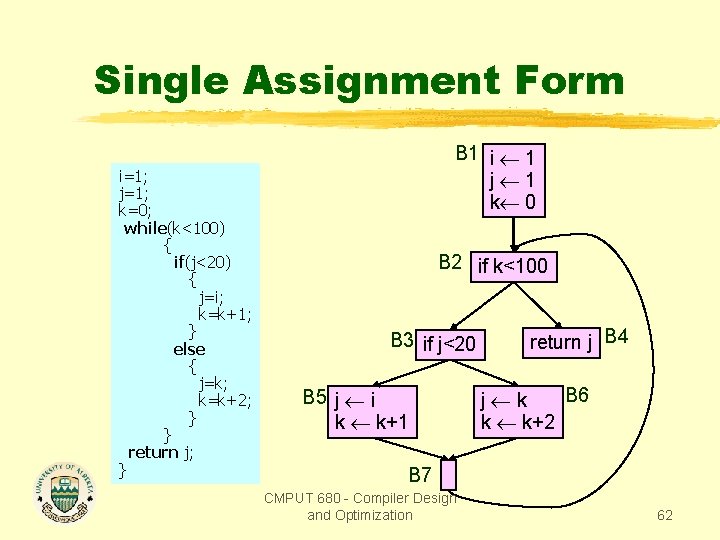
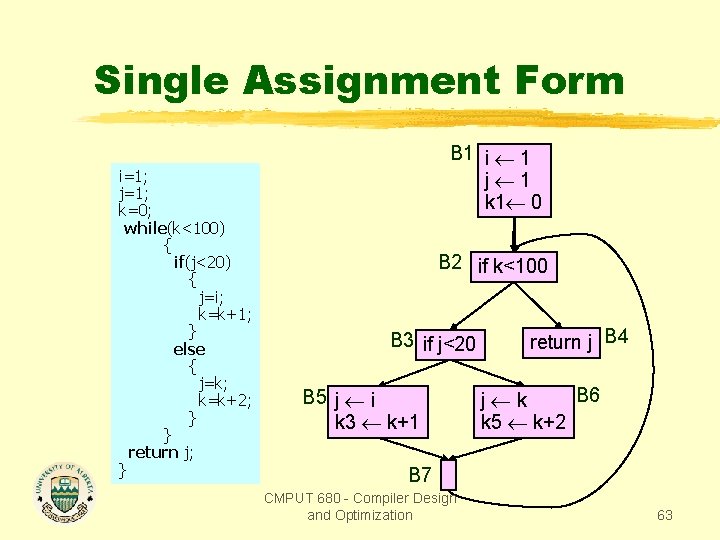
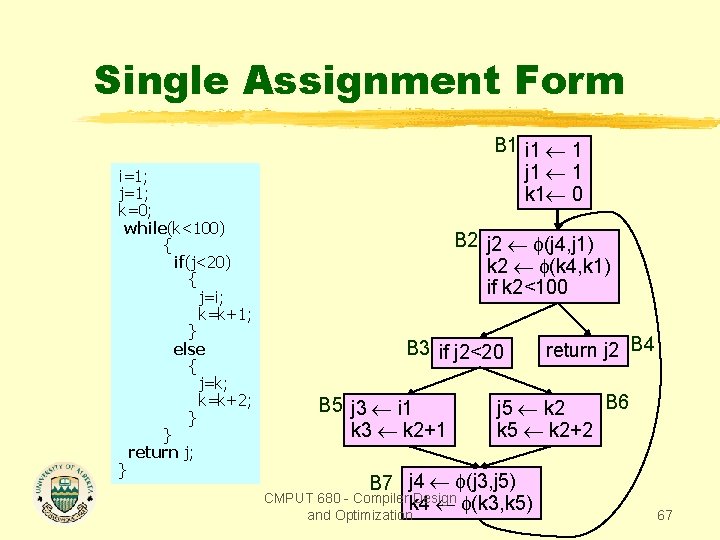
Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 j 1 k 0 B 2 if k<100 B 3 if j<20 B 5 j i k k+1 return j B 4 B 6 j k k k+2 B 7 CMPUT 680 - Compiler Design and Optimization 62

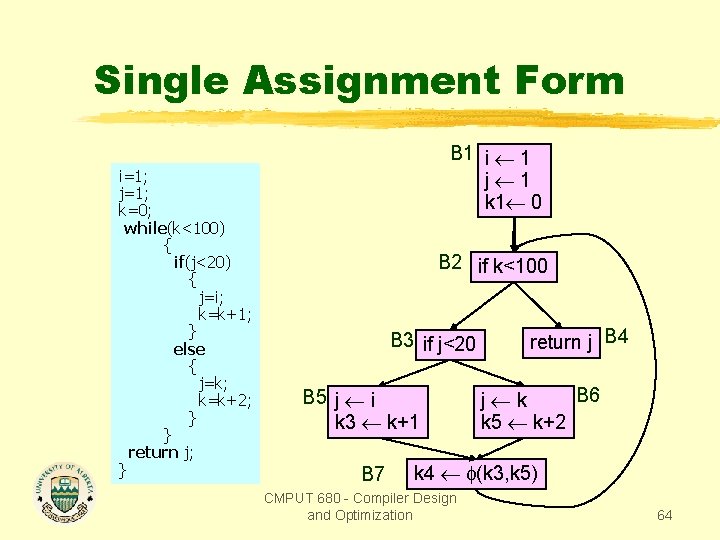
Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 j 1 k 1 0 B 2 if k<100 B 3 if j<20 B 5 j i k 3 k+1 return j B 4 B 6 j k k 5 k+2 B 7 CMPUT 680 - Compiler Design and Optimization 63

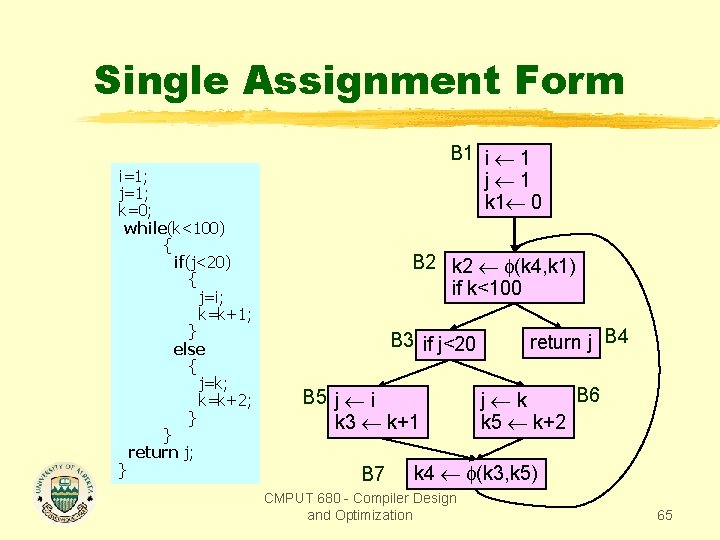
Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 j 1 k 1 0 B 2 if k<100 B 3 if j<20 B 5 j i k 3 k+1 B 7 return j B 4 B 6 j k k 5 k+2 k 4 (k 3, k 5) CMPUT 680 - Compiler Design and Optimization 64

Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 j 1 k 1 0 B 2 k 2 (k 4, k 1) if k<100 B 3 if j<20 B 5 j i k 3 k+1 B 7 return j B 4 B 6 j k k 5 k+2 k 4 (k 3, k 5) CMPUT 680 - Compiler Design and Optimization 65

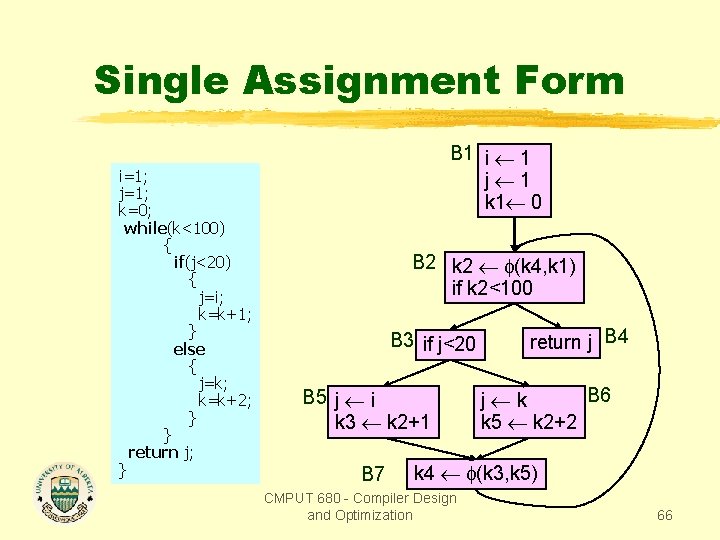
Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 j 1 k 1 0 B 2 k 2 (k 4, k 1) if k 2<100 B 3 if j<20 B 5 j i k 3 k 2+1 B 7 return j B 4 B 6 j k k 5 k 2+2 k 4 (k 3, k 5) CMPUT 680 - Compiler Design and Optimization 66

Single Assignment Form i=1; j=1; k=0; while(k<100) { if(j<20) { j=i; k=k+1; } else { j=k; k=k+2; } } return j; } B 1 i 1 1 j 1 1 k 1 0 B 2 j 2 (j 4, j 1) k 2 (k 4, k 1) if k 2<100 B 3 if j 2<20 B 5 j 3 i 1 k 3 k 2+1 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) (k 3, k 5) CMPUT 680 - Compiler Design k 4 and Optimization return j 2 B 4 67

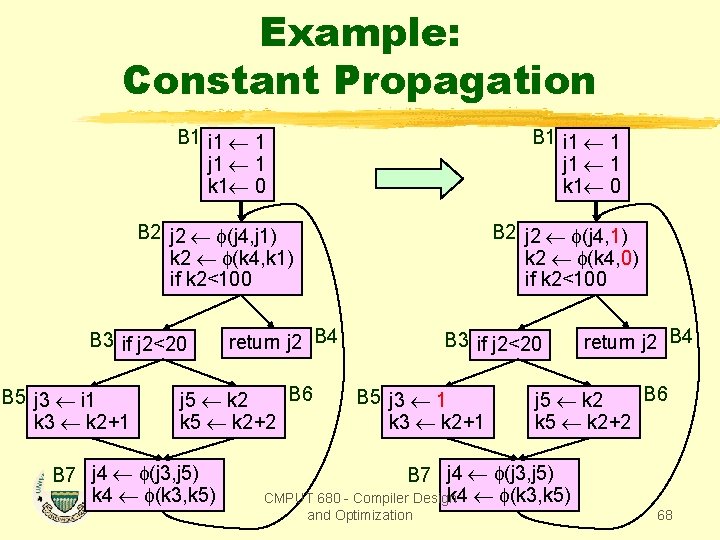
Example: Constant Propagation B 1 i 1 1 j 1 1 k 1 0 B 2 j 2 (j 4, j 1) k 2 (k 4, k 1) if k 2<100 B 3 if j 2<20 B 5 j 3 i 1 k 3 k 2+1 B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) k 4 (k 3, k 5) B 3 if j 2<20 B 5 j 3 1 k 3 k 2+1 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) k 4 (k 3, k 5) CMPUT 680 - Compiler Design and Optimization 68

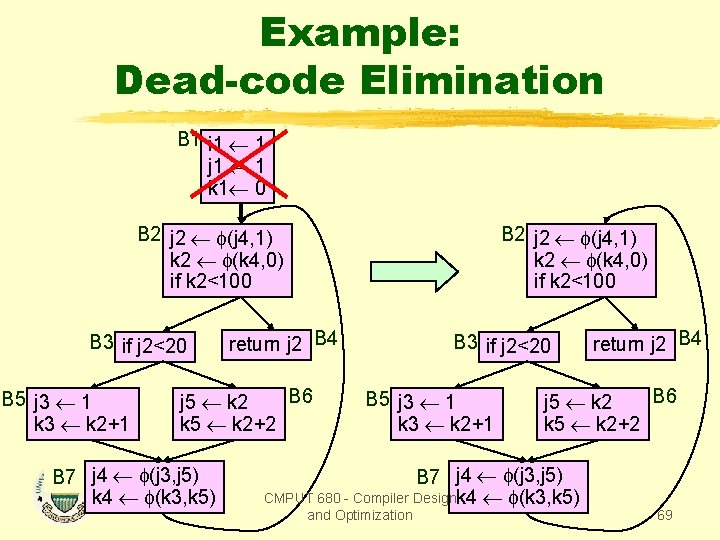
Example: Dead-code Elimination B 1 i 1 1 j 1 1 k 1 0 B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 3 if j 2<20 B 5 j 3 1 k 3 k 2+1 B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) k 4 (k 3, k 5) B 3 if j 2<20 B 5 j 3 1 k 3 k 2+1 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) CMPUT 680 - Compiler Designk 4 (k 3, k 5) and Optimization return j 2 B 4 69

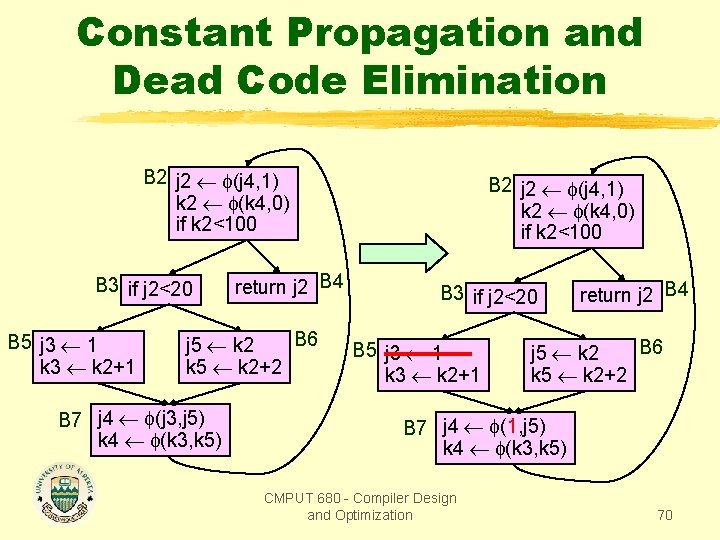
Constant Propagation and Dead Code Elimination B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 3 if j 2<20 B 5 j 3 1 k 3 k 2+1 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (j 3, j 5) k 4 (k 3, k 5) B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 3 if j 2<20 B 5 j 3 1 k 3 k 2+1 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (1, j 5) k 4 (k 3, k 5) CMPUT 680 - Compiler Design and Optimization 70

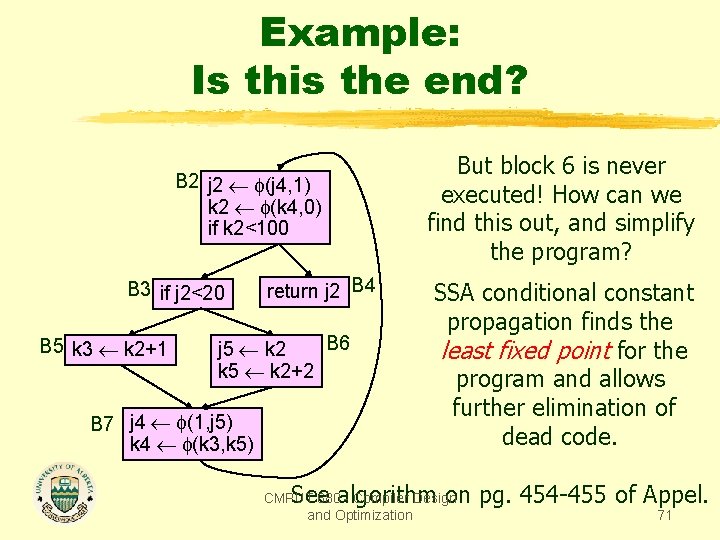
Example: Is this the end? B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 3 if j 2<20 B 5 k 3 k 2+1 return j 2 B 4 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (1, j 5) k 4 (k 3, k 5) But block 6 is never executed! How can we find this out, and simplify the program? SSA conditional constant propagation finds the least fixed point for the program and allows further elimination of dead code. See algorithm on pg. 454 -455 of Appel. CMPUT 680 - Compiler Design and Optimization 71

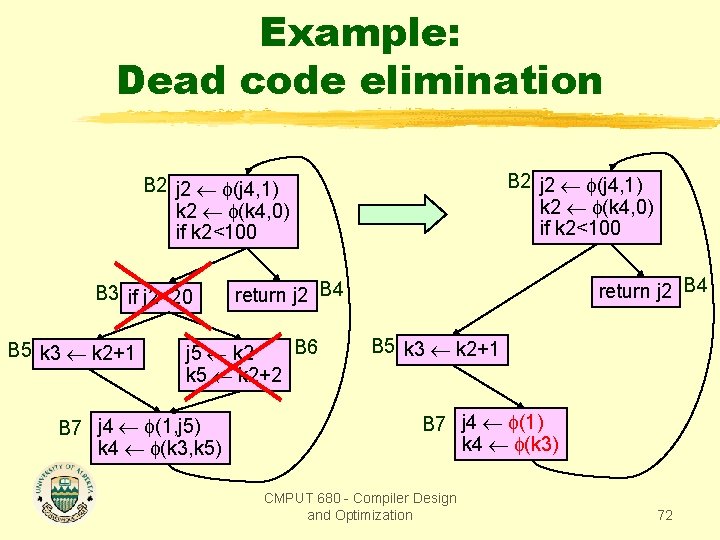
Example: Dead code elimination B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 3 if j 2<20 B 5 k 3 k 2+1 B 6 j 5 k 2 k 5 k 2+2 B 7 j 4 (1, j 5) k 4 (k 3, k 5) return j 2 B 4 B 5 k 3 k 2+1 B 7 j 4 (1) k 4 (k 3) CMPUT 680 - Compiler Design and Optimization 72

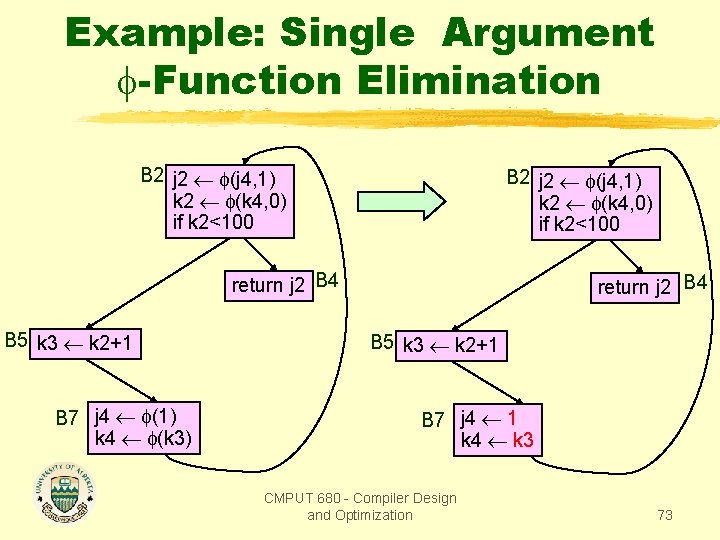
Example: Single Argument -Function Elimination B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 return j 2 B 4 B 5 k 3 k 2+1 B 7 j 4 (1) k 4 (k 3) return j 2 B 4 B 5 k 3 k 2+1 B 7 j 4 1 k 4 k 3 CMPUT 680 - Compiler Design and Optimization 73

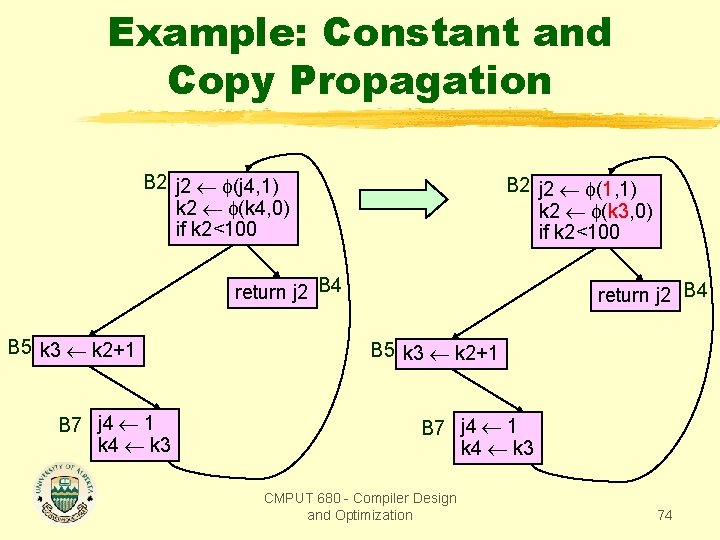
Example: Constant and Copy Propagation B 2 j 2 (j 4, 1) k 2 (k 4, 0) if k 2<100 B 2 j 2 (1, 1) k 2 (k 3, 0) if k 2<100 return j 2 B 4 B 5 k 3 k 2+1 B 7 j 4 1 k 4 k 3 CMPUT 680 - Compiler Design and Optimization 74

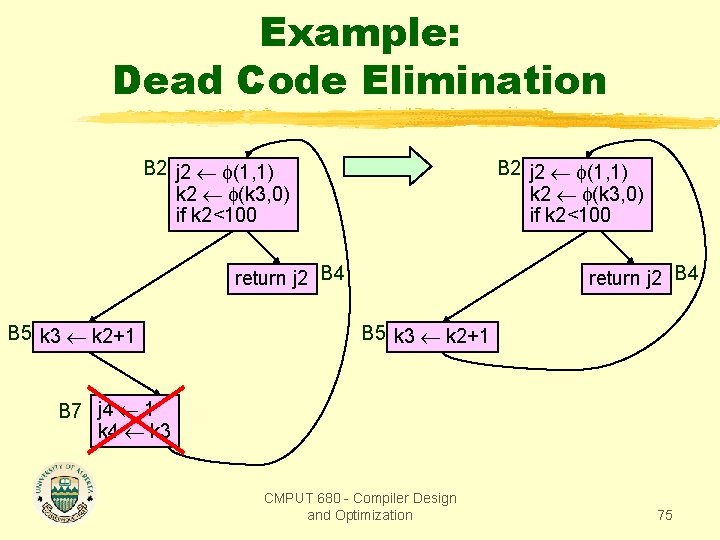
Example: Dead Code Elimination B 2 j 2 (1, 1) k 2 (k 3, 0) if k 2<100 return j 2 B 4 B 5 k 3 k 2+1 B 7 j 4 1 k 4 k 3 CMPUT 680 - Compiler Design and Optimization 75

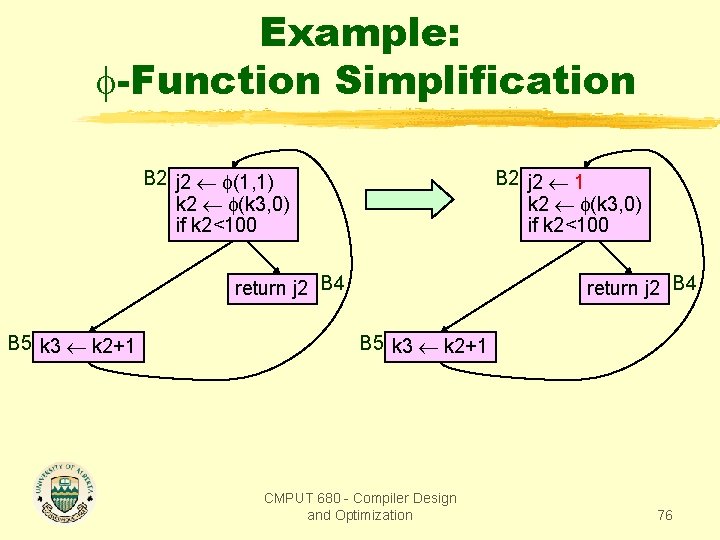
Example: -Function Simplification B 2 j 2 (1, 1) k 2 (k 3, 0) if k 2<100 B 2 j 2 1 k 2 (k 3, 0) if k 2<100 return j 2 B 4 B 5 k 3 k 2+1 CMPUT 680 - Compiler Design and Optimization 76

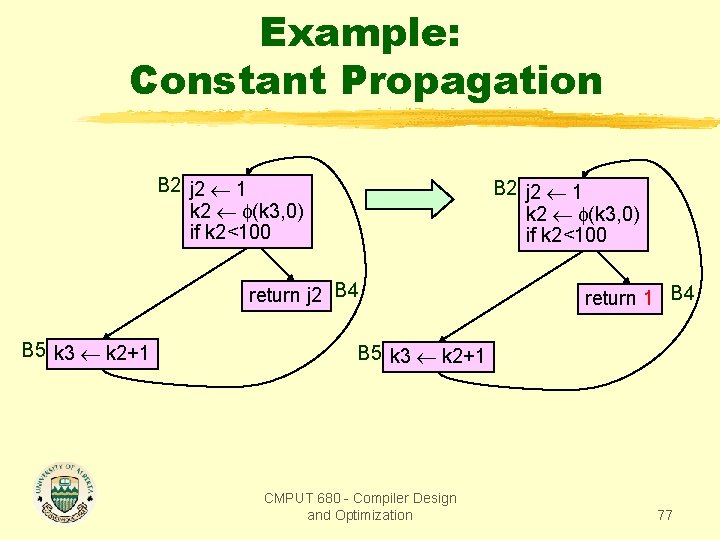
Example: Constant Propagation B 2 j 2 1 k 2 (k 3, 0) if k 2<100 return j 2 B 4 B 5 k 3 k 2+1 return 1 B 4 B 5 k 3 k 2+1 CMPUT 680 - Compiler Design and Optimization 77

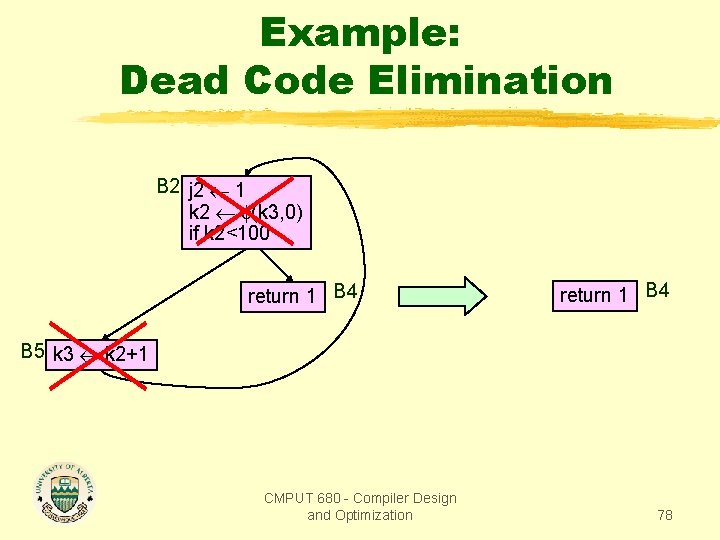
Example: Dead Code Elimination B 2 j 2 1 k 2 (k 3, 0) if k 2<100 return 1 B 4 B 5 k 3 k 2+1 CMPUT 680 - Compiler Design and Optimization 78